考虑余震和耗能梁损伤的K-EBF结构抗震性能分析










摘 要:针对构件失效会改变结构原有受力状态,同时建筑物可能会因余震的影响而产生严重破坏甚至倒塌的问题,研究了耗能梁构件损伤失效和余震对K形偏心支撑钢框架(K-EBF)结构抗震性能的影响。对12层和18层K-EBF结构算例以最大层间位移角为地震需求参数,峰值地震加速度(PGA)为地震动强度参数进行了增量动力分析、结构易损性分析和抗倒塌性能评估。结果表明:同时考虑余震以及耗能梁损伤失效与均不考虑相比,12层和18层结构在设防地震时的最大层间侧移角θmax分别增大2.3%和8.4%,重度损伤失效概率分别增大0.6%和2.8%;罕遇地震时的θmax分别增大21.0%和42.1%,重度损伤失效概率分别增大11.6%和19.4%;另外,12层和18层结构的最小抗倒塌储备系数分别下降了32.1%和31.2%;总体上,余震会加剧结构损伤累积,其对结构的影响程度会随地震动强度的变大而增加;在考虑耗能梁构件损伤失效后,结构不同极限状态下失效概率会进一步增大,造成结构的最小抗倒塌储备系数进一步下降;因此,在K-EBF结构抗震性能分析时应充分考虑余震和耗能梁损伤失效所造成的影响,以真实反映结构地震作用下的响应。将耗能梁的损伤失效和余震的影响同时纳入考虑范围可更全面地分析K-EBF结构的抗震性能,为抗震设计提供更可靠的依据。
关键词:结构设计;偏心支撑结构;主余震;抗倒塌性能;易损性分析;耗能梁失效
中图分类号:TU391
文献标识码:A
DOI:10.7535/hbkd.2024yx05007
Seismic performance of K-EBF structures considering
aftershock sequences and link failure
YU Haifeng1,ZHU Yifan1,FANG Bin2,JIN Tianjiao1,MA Kang1,LI Yong1
(1.School of Civil Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China;
2.Hebei Province Green Building Promotion and Construction Engineering Standards Compilation Center,
Shijiazhuang, Hebei 050Cm/lscbxThZE6fYSI2df9g==051, China)
Abstract:Aiming at the problems that the failure of members can change the stress state of the structure, and the building may be severely damaged or even collapsed due to aftershock sequences, the effect of aftershock sequences and link failure on the seismic performance of K-eccentrically braced steel frames (K-EBF) was investigated. Incremental dynamic analysis, fragility analysis, and collapse-resistant performance evaluations of 12-story and 18-story K-EBF were conducted by using the maximum inter-story drift as the seismic demand parameter and peak seismic acceleration as the ground motion intensity parameter. The results show that compared with non-considering the effect of aftershock sequences and link failure, under the fortification earthquakes, the two factors (aftershock sequences and link failure) make the θmax of the 12-story and 18-story K-EBF structures increase by 2.3% and 8.4%, and the probability of severe damage increase by 0.6% and 2.8%, respectively; Under rare earthquakes, the θmax of the 12-story and 18-story K-EBF structures increase by 21.0% and 42.1%, and the probability of severe damage failure increase by 11.6% and 19.4%, respectively; In addition, the minimum structural collapse reserve factor decreases by 32.1% and 31.2% for 12-story and 18-story structures, respectively; Overall, aftershock sequences will aggravate the structure damage accumulation, and the negative effect on the structure increases with the intensity of the earthquakes;The failure probabilities of different limit state will further increase after considering the link failure, which will result in a further decrease with the minimum structural collapse reserve factor; Therefore, the effects caused by aftershock sequences and link failure should be fully considered in the seismic performance analysis of K-EBF to reveal the structural real dynamic response under earthquakes. Taking both the damage failure of link failure and the effect of aftershocks into consideration can comprehensively analyze the seismic performance of K-EBF structures, which provides a more reliable basis for seismic design.
Keywords:structural designs;eccentrically braced steel structures;main-aftershock sequence;collapse resistance;fragility analysis;link failure
K形偏心支撑钢框架(K-EBF)是常用的一种钢结构抗侧力体系,地震作用下,同层支撑之间的耗能梁段是结构主要的耗能区域。历次震害表明,在地震强震(主震)过后,随之会发生一系列余震,此时主震对结构造成的损伤往往未能得到及时修缮,余震可能会比主震更具有破坏性[1]。如2023年土耳其的7.8级主震之后,有40余次5.0级以上余震发生,造成了大量房屋倒塌。因此,余震对结构的影响不容忽视。
近年来,不少学者对K-EBF 结构抗震性能开展了相关研究。叶重阳等[2]研究了耗能梁段的连接构造对K-EBF 结构抗震性能的影响,发现采用外伸端板连接时承载能力和耗能能力均高于平齐端板连接试件;于海丰等[3]研究了带骨式削弱弯曲型耗能梁的K-EBF 结构抗震性能,发现骨式削弱设计及加劲肋间距能够使耗能梁端部翼缘更大区域出现弯曲塑性变形,提升耗能能力;苏明周等[4]认为在带有可替换耗能梁的K-EBF 结构中,梁柱采用刚接时结构具有较好的抗震性能;YIN等[5]研究了将偏心支撑钢框架的传统支撑改成防屈曲约束支撑后的结构抗震性能;田小红等[6]研究了不同强度组合、不同层数高强钢组合的K-EBF 结构抗震性能。相关研究证实,K-EBF结构在抗震方面表现卓越,其中耗能梁作为关键构件,对结构性能的影响尤为突出。
在主余震及结构易损性方面:杜云霞等[7]研究发现尽管余震强度较低,但经历连续2次地震作用,结构损伤累计效益明显,较单次地震作用损伤提高较大;于晓辉等[8]研究了人工构造主余震的损伤特征,发现余震所造成的增量损伤不可忽视,但人工构造主余震会高估结构的增量损伤;JEON等[9]研究了老旧钢筋混凝土框架结构在主余震作用下的地震易损性,发现余震对结构倒塌概率的影响显著,最高可达30%。GODA等[10]研究了真实与构造主余震地震动下木结构的倒塌易损性,发现余震使结构响应增加5%~20%。夏贇[11]开展了主余震序列作用下的砌体结构易损性研究,证明余震会对结构产生额外的附加损伤,主余震序列作用下结构呈现出比单独主震作用下高一个破坏等级的趋势。余震对结构动力响应和损伤的影响显著,在设计分析时需充分考虑其所造成的影响,以保证结构安全。
对K-EBF结构而言,地震作用下,耗能梁构件失效会改变结构原有的受力特征,同时余震可能会加剧结构抗震性能劣化。目前对K-EBF 结构抗震性能的研究基本未涉及主余震,也很少考虑耗能梁构件失效退出工作对结构的影响,因此开展考虑耗能梁损伤失效和余震影响的K-EBF 结构抗震性能研究是十分必要的。
1 结构分析模型
1.1 K-EBF 结构模型
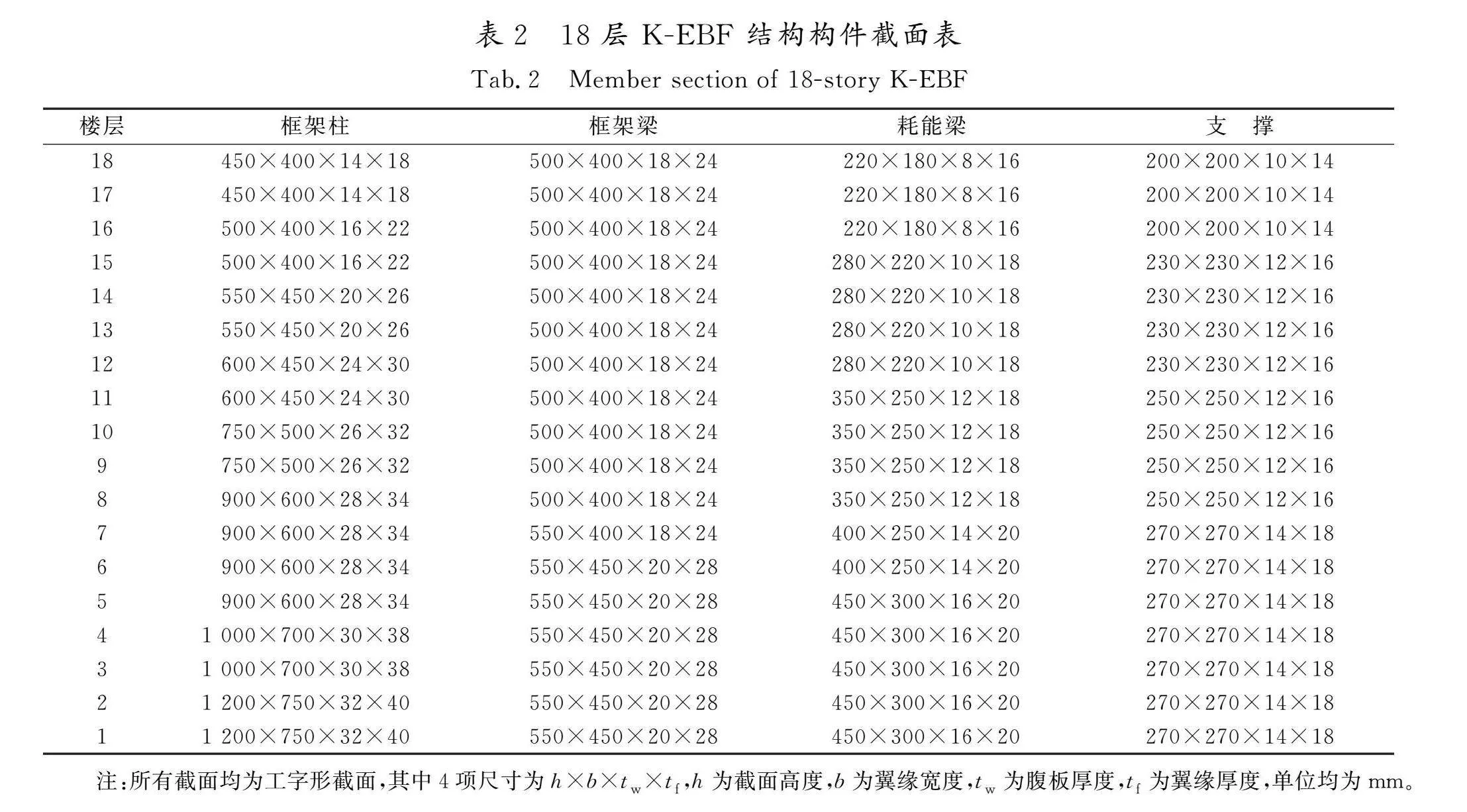
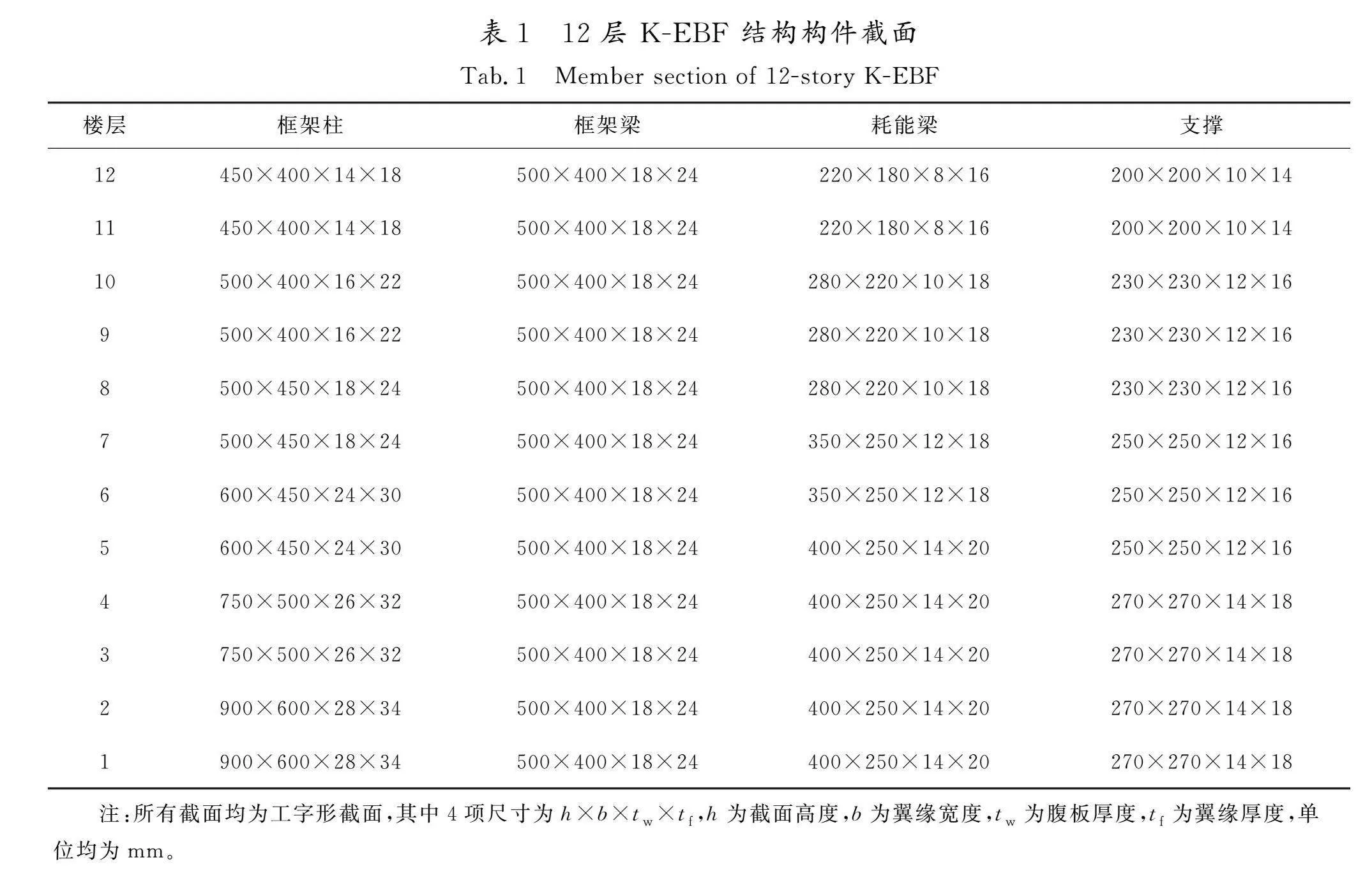
本文设计了12层和18层的K-EBF 结构模型,横向5跨,偏心支撑位于横向中间跨,每跨跨度7.8 m,层高3.9 m,耗能梁长度1 m,e/l=0.13。框架梁与框架柱间采用刚接,支撑两端与框架梁和框架柱间采用铰接,如图1所示。假定建筑所在地区抗震设防烈度8度(0.2g),场地类别为Ⅲ类,地震设计分组为第2组。上人屋面恒荷载和活荷载标准值分别取8.25 kN/m2和2 kN/m2;楼面恒荷载和活荷载标准值分别取7.8 kN/m2和2 kN/m2[12-13],结构构件尺寸见表1和表2。所有构件均采用Q345钢材
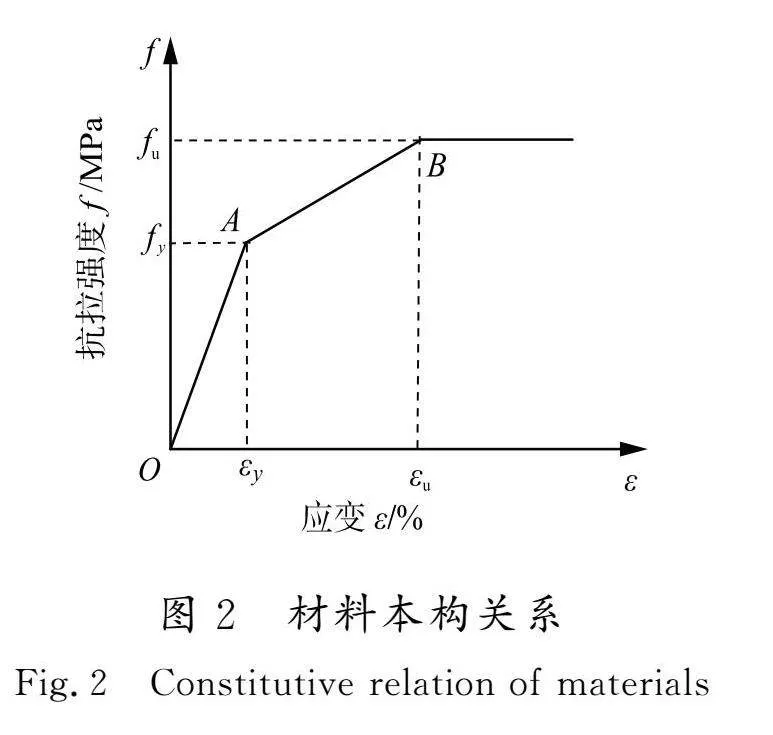
(钢材的各项力学性能见表3),截面均为焊接工字形截面。Q345钢材采用屈服点和极限点定义的三折线本构模型,如图2所示。在此模型中,OA段表示材料的弹性阶段,斜率代表钢材的弹性模量E,反映了材料在弹性范围内的应力与应变关系;AB段表示材料的塑性强化阶段,斜率取0.01E,体现了钢材在塑性变形过程中的刚度降低特性。
1.2 K-EBF 数值模型
取一榀钢框架为分析对象,如图1 b)所示。采用ABAQUS软件建立结构有限元模型,各构件均采用三节点Timokenko梁(B32梁单元),将结构楼层的屋面和楼面荷载等效为节点荷载,采用mass质量单元模拟。梁柱构件设置平面外约束;柱底部设置为固接,约束全部自由度;支撑构件考虑初始缺陷影响,缺陷按1/500杆长的面外弯曲考虑[14]。
通过前期研究,课题组以转角为需求参数定义了耗能梁段在不同极限状态下的损伤限值,转角的计算方法见文献[15],得出耗能梁转角达到0.098 rad后,往往发生腹板、翼缘屈曲严重,焊缝断裂等现象,其处于严重损伤状态,这时耗能梁失去了抗弯能力,仅能传递轴向作用。因此,本文分析时,当耗能梁的转角达到0.098 rad时,耗能梁与框架梁的连接由刚接改为铰接,具体通过ABAQUS软件中激活、杀死单元来实现。首先建立结构整体模型,在每层耗能梁单元初始位置处建立相同单元(与框架梁铰接,未激活前不承受任何荷载,与框架梁同时运动)并将其全部杀死,待到耗能梁转角达到损伤限值时激活该单元,同时杀死原始耗能梁单元,以此来模拟耗能梁损伤失效对结构的影响。
1.3 自振特性
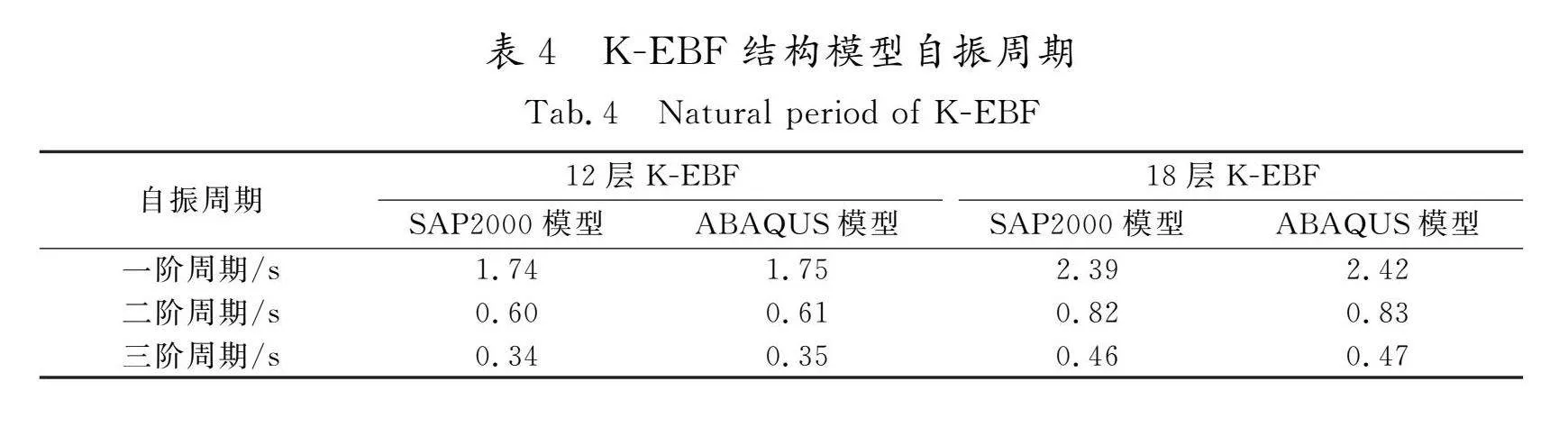
表4给出了基于SAP2000软件和ABAQUS软件计算的模型结构前3阶自振周期。可见,2种软件计算的结构周期基本一致,表明采用ABAQUS软件建模合适。
2 地震动记录及主余震的构造
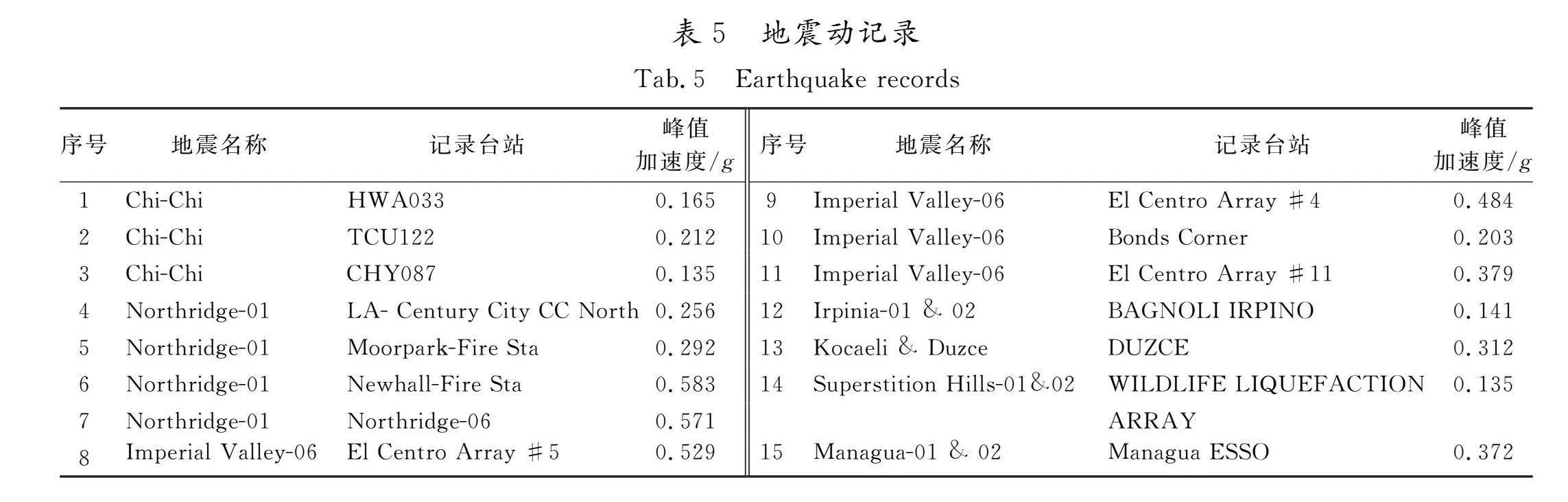
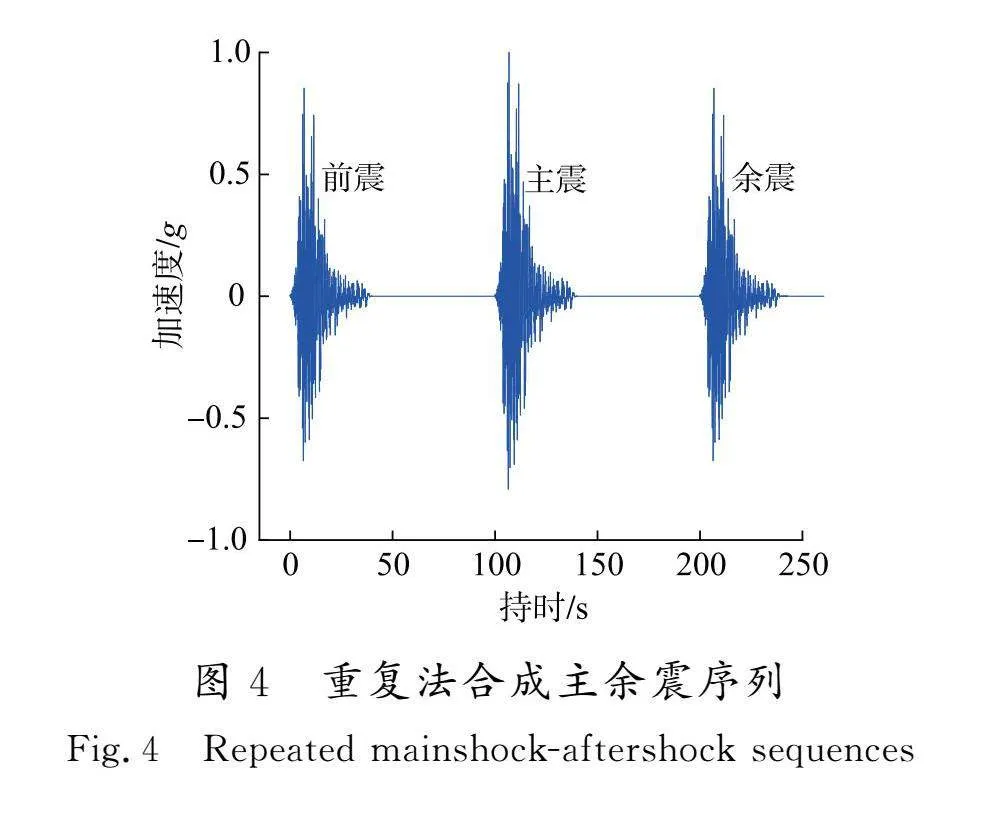
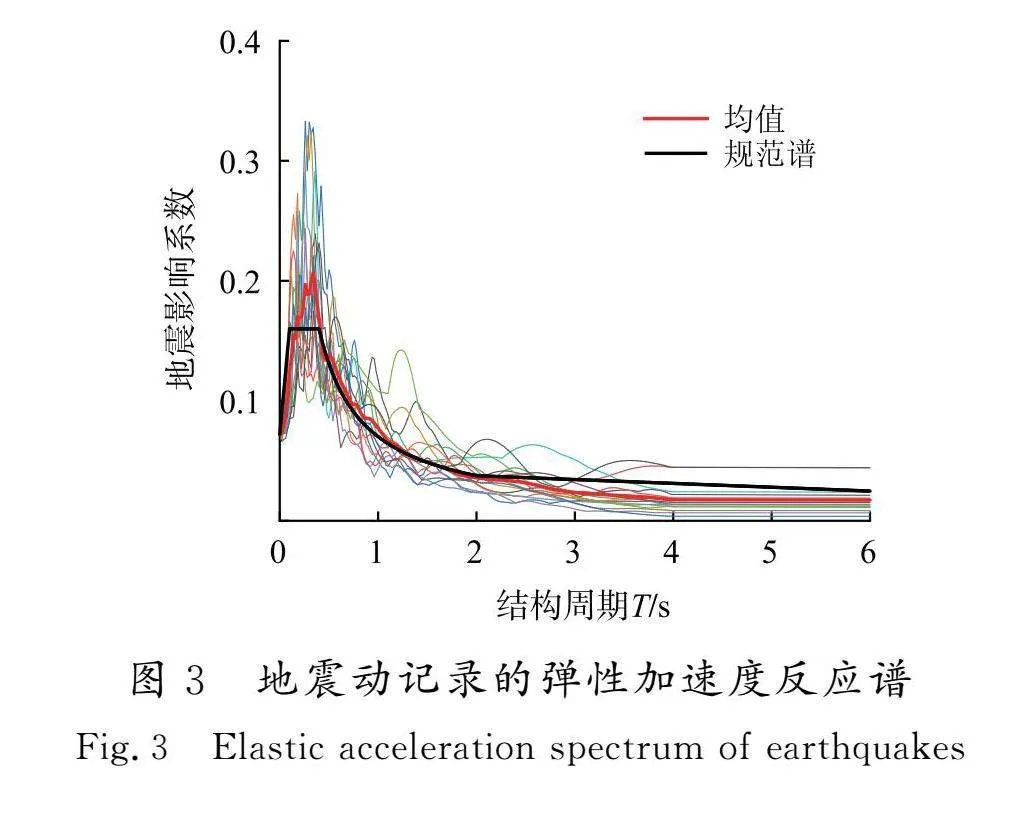
本文选用了15条天然远场地震波(见表5)作为输入地震动荷载,地震记录的加速度反应谱见图3。Hatzigeorgiou和Beskos提出合成主余震工况为前震+主震+余震的模式,Gutenberg-Richter定律和Joyner-Boore经验公式认为余震的峰值地震加速度(PGA)和主震的PGA的调幅系数应为0.852 6,因此本文参照相关研究,采用重复法合成主余震地震动[16]。重复主余震按(0.852 6,1,0.852 6)进行合成,如图4所示,每次地震动后添加60 s空白时程,以保证地震动作用后动力响应完全停止[17]。
3 基于最大层间位移角的增量动力分析
增量动力分析(IDA)是基于大量地震作用的结构抗震性能评估方法,能够记录结构从弹性状态到屈服,再到弹塑性状态,最终倒塌的演变过程[18]。为研究耗能梁损伤失效和余震对K-EBF 结构抗震性能的影响,分别对在单独主震和主余震作用下、未考虑耗能梁损伤失效和考虑耗能梁损伤的K-EBF 结构进行 IDA 分析。
最大层间位移角与结构的节点转动能力、构件破坏程度和层间倒塌能力有关,能较好反映结构在地震作用下的破坏状态[19]。因此,本文选用结构最大层间位移角(θmax)为地震需求参数,以PGA作为地震动强度参数进行IDA 分析。
3.1 余震影响分析
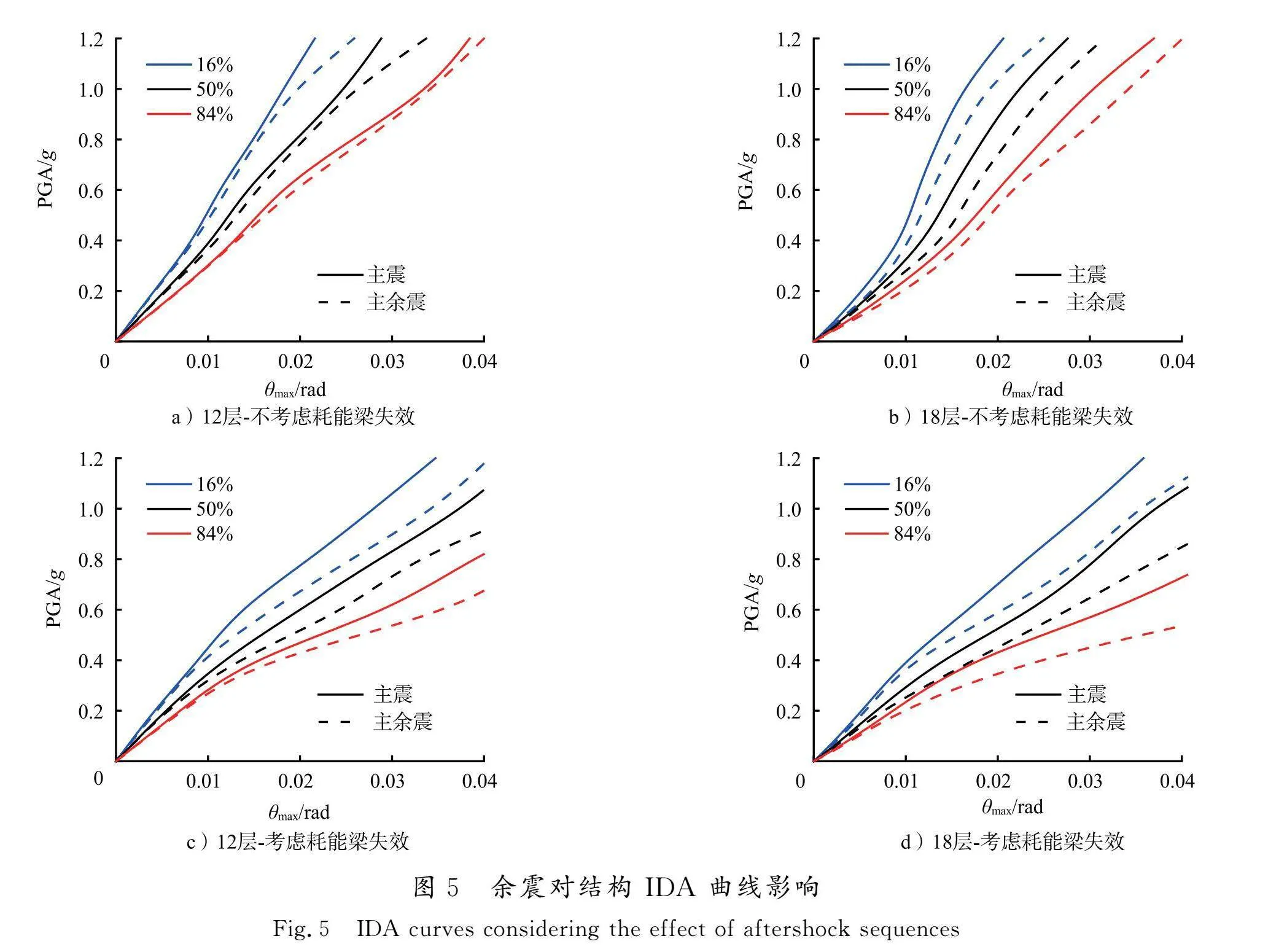
考虑主余震和仅考虑主震时12层和18层 K-EBF 结构的 IDA 曲线如图5所示。可见,主余震作用下的分位线均在主震作用下的下方,说明余震会增大结构的动力响应。若不考虑耗能梁损伤失效,余震使得12层和18层结构的θmax在设防地震(PGA=0.2g)时分别增大1.7%和6.8%,在罕遇地震(PGA=0.4g)时分别增大6.2%和18.1%。若考虑耗能梁损伤失效,余震使得12层和18层结构的θmax在设防地震(PGA=0.2g)时分别增大2.1%和8.0%,在罕遇地震(PGA=0.4g)时分别增大11.1%和27.0%。显然,随着输入地震动的增大,余震对结构动力响应的影响呈明显渐增趋势,且影响越来越显著。这说明在低地震动强度下,结构整体塑性发展不充分,表现出较好的刚度和强度特性,能够有效抵抗地震作用;随着地震动强度的增强,结构逐渐进入弹塑性阶段,由于塑性变形的累积使结构的刚度和强度逐渐退化,此时余震的影响变得更加显著,会进一步加剧结构的损伤。
3.2 耗能梁损伤失效影响分析
考虑耗能梁损伤失效和不考虑耗能梁损伤失效时结构的IDA曲线如图6所示。可见,考虑耗能梁损伤失效的分位线均在不考虑耗能梁损伤失效影响的下方,说明耗能梁损伤失效会增大结构的动力响应。
由图6可知,PGA≤0.2g时,由于绝大多数耗能梁段未达到损伤限值,是否考虑耗能梁损伤失效对结构 IDA 曲线影响较小。罕遇地震(PGA=0.4g)时,若仅考虑主震作用,耗能梁损伤失效使12层和18层结构的θmax分别增加了8.8%和11.9%;若考虑主余震作用,耗能梁损伤失效使12层和18层结构的θmax分别增加了14.0%和20.3%。显然,随着地震动强度的增大(尤其在PGA>0.2g之后),耗能梁的损伤失效会增大结构的动力响应,且随着PGA的增大,影响越来越显著。说明在低地震动强度下,耗能梁通过塑性变形耗散地震能量,从而减轻了主体结构的损伤。随着地震动强度的逐渐增强,耗能梁因达到其损伤限值而发生失效,导致其性能下降,进而使结构刚度大幅下降,增大了结构的动力响应。
3.3 主余震及耗能梁损伤失效综合影响分析
同时考虑余震以及耗能梁损伤失效与均不考虑上述二者影响的结构 IDA 曲线如图7所示。可见,同时考虑余震以及耗能梁损伤失效时,使得12层和18层结构的θmax在设防地震(PGA=0.2g)时分别增大2.3%和8.4%,在罕遇地震(PGA=0.4g)时分别增大21.0%和42.1%,均大于单独考虑余震或耗能梁损伤失效时对结构θmax的影响。尤其在PGA>0.2g之后,随着地震强度的增加,同时考虑余震以及耗能梁损伤失效与均不考虑上述二者影响的结构θmax之间的差异越发明显。这是因为某层耗能梁损伤失效后,该层承担地震作用的能力变小,耗能能力降低,势必将加大其临近楼层的动力响应。在余震发生时,累积的损伤会进一步加剧,使得结构受到更严重的破坏。因此,余震和耗能梁损伤对结构的影响不能忽略,K-EBF结构抗震性能分析应充分加以考虑。
4 结构的易损性分析
结构的地震易损性是指在不同强度地震动下,结构发生某种程度损伤的可能性。通过计算结构在给定的PGA下,结构的地震反应(θmax)超出其抗震能力(θc)的条件概率,定量评估结构的整体地震易损性[20]。
Pf=Φ[ln[α(PGA)β/θc]σ2θc+σ2θmax],
(1)
ln θmax=a+bln PGA,(2)
式中:Pf为结构极限状态失效概率;α=ea,β=b,其中a、b为式(2)线性回归系数;θc为结构极限状态层间位移角限值;Φ[x] 为标准正态分布函数。
4.1 概率地震需求分析
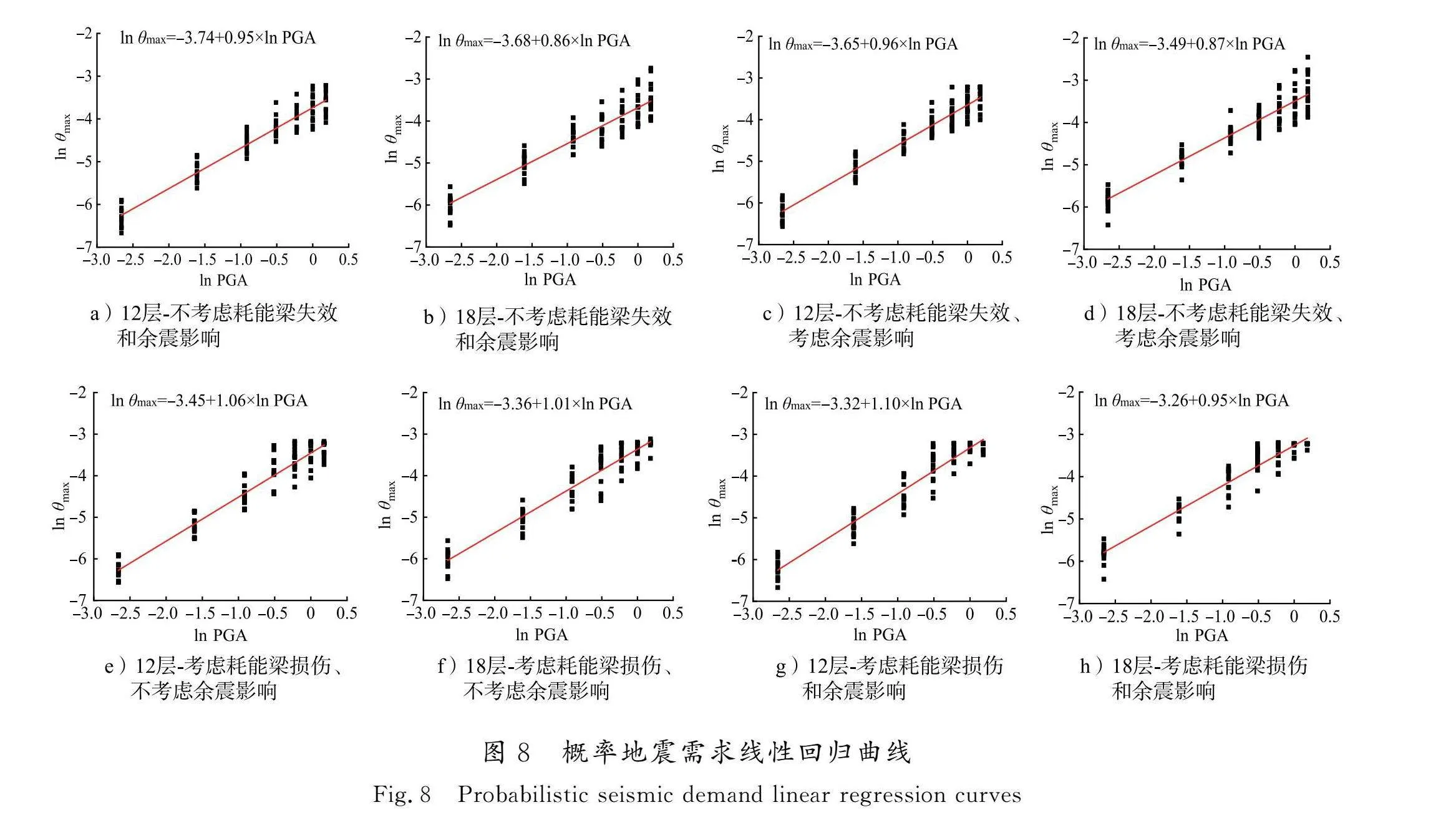
在得到图5及图6所示的结构 IDA 曲线后,基于式(2)对 PGA和θmax的自然对数样本进行线性回归分析,得到结构的概率地震需求线性回归曲线,如图8所示。
4.2 结构易损性曲线
根据文献[21]的建议值,以最大层间位移角θmax为结构需求参数指标,定义了结构的5种破坏状态,如表6所示。结构极限状态限值分别为轻度损伤(1/250)、中度损伤(1/100)、重度损伤(1/50)、倒塌(1/25)。
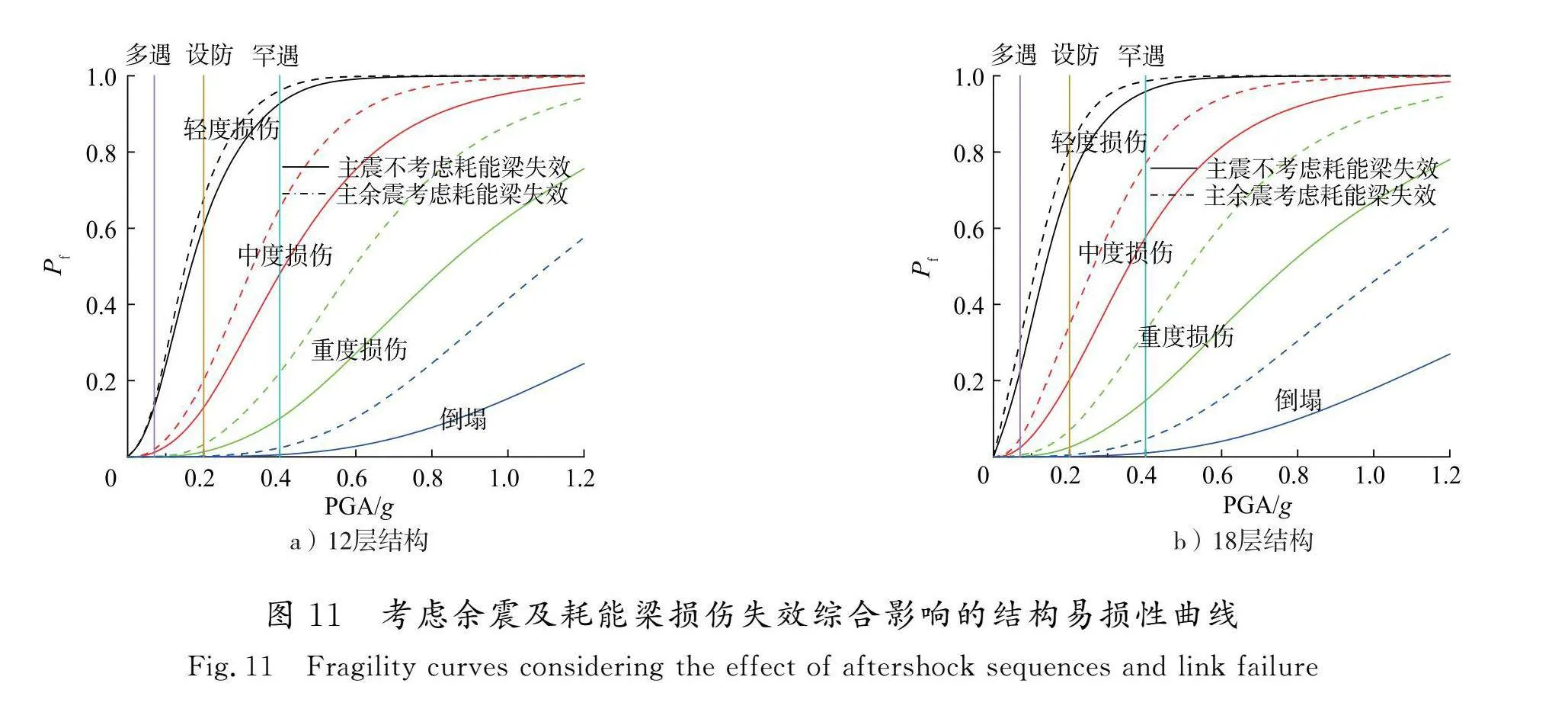
按照式(1),分别对12层和18层结构进行地震下结构易损性分析,其结构易损性曲线见图9—图11。
4.2.1 余震影响分析
图9给出了12层和18层K-EBF 结构分别在单独主震和主余震作用、不同极限状态下的失效概率。若不考虑耗能梁损伤失效,余震使得12层和18层结构的重度损伤失效概率在设防地震(PGA=0.2g)时分别增大0.2%和1.4%,在罕遇地震(PGA=0.4g)时分别增大3.1%和8.9%。若考虑耗能梁损伤失效,余震使得12层和18层结构的重度损伤失效概率在设防地震(PGA=0.2g)时分别增大0.3%和2.3%,在罕遇地震(PGA=0.4g)时分别增大4.7%和10.1%。考虑余震作用后,结构的各极限状态失效概率变大,地震动强度越大,余震对结构影响越大,使结构向更不利的破坏状态发展。因此,在分析结构抗震性能时忽略余震的影响,将会高估结构的抗震能力。
4.2.2 耗能梁损伤失效影响分析
考虑和不考虑耗能梁损伤失效时结构的易损性曲线如图10所示。若仅考虑主震作用,耗能梁损伤失效使12层和18层结构的重度损伤失效概率在设防地震(PGA=0.2g)时分别增大0.3%和0.5%;在罕遇地震(PGA=0.4g)时分别增大6.8%和9.3%。若考虑主余震作用,耗能梁损伤失效使12层和18层结构的重度损伤失效概率在设防地震(PGA=0.2g)时分别增大0.4%和1.4%;在罕遇地震(PGA=0.4g)时分别增大9.1%和10.5%。随着地震动强度的增大,耗能梁的损伤失效会增大结构各极限状态的失效概率且影响越来越大。
4.2.3 主余震及耗能梁损伤失效综合影响分析
同时考虑余震以及耗能梁损伤失效与均不考虑上述二者影响的结构易损性曲线如图11所示。同时考虑余震以及耗能梁损伤失效使得12层和18层结构的重度损伤失效概率在设防地震(PGA=0.2g)时分别增大0.6%和2.8%,在罕遇地震(PGA=0.4g)时分别增大11.6%和19.4%,均大于单独考虑余震或耗能梁损伤失效时对结构失效概率的影响。随着地震动强度的变大,结构的重度损伤和倒塌概率增大加快,对结构造成的破坏影响增大。
5 结构抗倒塌性能评估
最小抗倒塌储备系数(CMRP=10%)不仅能够反映结构对于“大震不倒”要求的安全储备,同时与中国设计规范紧密结合[22-23]。文献[24]给出中国抗震设防要求定量验算指标(见式(3)),要求CMRP=10%不应小于1.0。
CMRP=10%=IMP=10%IM罕遇=PGAP=10%PGA罕遇 , (3)
式中:IMP=10%为易损性曲线中结构有10%概率处于倒塌损伤状态时所对应的地震动强度值;IM罕遇为结构在罕遇地震时所对应的地震动强度值。
12层和18层 K-EBF 结构不同工况(主余震、耗能梁损伤)下的最小抗倒塌储备系数如表7所示。若不考虑耗能梁损伤,余震使12层和18层结构的CMRP=10%分别下降0.226(10.9%)和0.276(14.5%);若考虑耗能梁损伤失效,余震使12层和18层结构的CMRP=10%下降0.167(10.0%)和0.184(12.3%)。若仅考虑主震作用,耗能梁的损伤失效使12层和18层结构的 CMRP=10%分别下降0.483(24.4%)和0.315(19.3%);若考虑主余震作用,耗能梁的损伤失效使12层和18层结构的 CMRP=10%分别下降0.542(24.8%)和0.407(21.3%)。对比同时考虑余震以及耗能梁损伤失效与均不考虑上述二者影响的最小抗倒塌储备系数,同时考虑二者影响使12层和18层结构的 CMRP=10%分别下降了0.709(32.1%)和0.591(31.2%)。余震和耗能梁的损伤失效会降低结构的抗倒塌储备系数,使结构更容易发生倒塌风险。另外,相比较而言,耗能梁损伤失效对最小抗倒塌储备系数的影响要高于余震的影响。
6 结 语
1)同时考虑余震以及耗能梁损伤失效使12层和18层结构的 θmax较不考虑二者影响在设防地震(PGA=0.2g)时分别增大了2.3%和8.4%,在罕遇地震(PGA=0.4g)时分别增大21.0%和42.1%,均大于单独考虑余震或耗能梁损伤失效时对结构θmax的影响。随着输入地震动的增大,余震和耗能梁损伤失效对结构动力响应的影响呈明显渐增趋势。
2)同时考虑余震以及耗能梁损伤失效使12层和18层结构的重度损伤失效概率较不考虑二者影响在设防地震(PGA=0.2g)时分别增大0.6%和2.8%,罕遇地震(PGA=0.4g)时分别增大11.6%和19.4%,均大于单独考虑余震或耗能梁损伤失效时对结构失效概率的影响,且随着地震动强度的变大,结构的重度损伤和倒塌概率增大加快,对结构造成的破坏影响增大,使结构向不利方向发展。
3)同时考虑余震以及耗能梁损伤失效使12层和18层结构的 CMRP=10%较不考虑上述二者影响分别下降了0.709(32.1%)和0.591(31.2%),造成结构倒塌的风险明显增大。相对而言,耗能梁损伤失效对CMRP=10%的影响要高于余震的影响。总体上,余震和耗能梁损伤对结构抗震性能及抗倒塌性能的影响不能忽视,应充分加以考虑。
在结构布置方面,对于高层建筑或跨度较大的K-EBF 结构,应适当增加偏心支撑及耗能梁的数量和密度,分散地震对结构的冲击。通过增大耗能梁的塑性耗能能力,可以减小地震对主要构件的损伤,降低楼层位移角,提高结构的整体稳定性和承载能力。在结构设计方面,应充分考虑耗能梁和余震对结构的影响,进行合理的截面设计,确保耗能梁能够在地震中有效地吸收和耗散能量,保证结构在地震作用下有足够的承载能力和刚度,进一步提高建筑的抗震性能。
本文采用梁单元模型虽然计算效率高,但存在无法直接显示结构局部变形、裂缝扩展、局部应力集中的问题。未来拟采用实体单元以提供更全面的模拟。
参考文献/References:
[1] 周
洲,于晓辉,吕大刚.主余震序列作用下钢筋混凝土框架结构的易损性分析及安全评估[J].工程力学,2018,35(11):134-145.
ZHOU Zhou,YU Xiaohui,LYU Dagang.Fragility analysis and safety evaluation of reinforced concrete frame structures subjected to mainshock-aftershock earthquake sequences[J].Engineering Mechanics,2018,35(11):134-145.
[2] 叶重阳,王新武,时强,等.耗能梁段连接构造对偏心支撑钢框架抗震性能的影响[J].工业建筑,2023,53(8):58-64.
YE Chongyang,WANG Xinwu,SHI Qiang,et al.Influence of the connection structure of energy dissipating beam section on the seismic performance of eccentrically braced steel frame[J].Industrial Construction,2023,53(8):58-64.
[3] 于海丰,王炜,吴杨周,等.带骨式削弱弯曲型耗能梁K形偏心支撑框架抗震性能研究[J].河北科技大学学报,2023,44(3):286-296.
YU Haifeng,WANG Wei,WU Yangzhou,et al.Study on seismic behaviour of K-eccentrically braced steel frame with dog-bone reduced flexural link[J].Journal of Hebei University of Science and Technology,2023,44(3):286-296.
[4] 苏明周,李慎,连鸣.K形偏心支撑钢框架的弹性抗侧刚度与极限承载力[J].西安建筑科技大学学报,2014,46(6):791-799.
SU Mingzhou,LI Shen,LIAN Ming.Elastic lateral stiffness and ultimate bearing capacity of K-shaped eccentric braced steel frames[J].Journal of Xi′an University of Architecture and Technology,2014,46(6):791-799.
[5] YIN Zhanzhong,YANG Bo,ZHANG Xiaobo.Design of an eccentrically buckling-restrained braced steel frame with web-bolted replaceable links[J].Journal of Constructional Steel Research,2022.DOI:10.1016/j.jcsr.2022.107250.
[6] 田小红,苏明周,连鸣,等.高强钢组合K形偏心支撑钢框架抗震性能分析[J].工程力学,2019,36(3):182-191.
TIAN Xiaohong,SU Mingzhou,LIAN Ming,et al.Analysis of aseismic performance of high strength steel composite K-eccentrically braced frames[J].Engineering Mechanics,2019,36(3):182-191.
[7] 杜云霞,公茂盛,谢礼立.两次地震作用下RC框架结构抗震能力分析方法研究[J].世界地震工程,2017,33(1):75-83.
DU Yunxia,GONG Maosheng,XIE Lili.Seismic analysis method of 4PQ36ypzxfD++ECZ+6dzMFiw74OUcHAOeR9NJbECWss=RC frame structure considering the excitations of twice earthquakes[J].World Earthquake Engineering,2017,33(1):75-83.
[8] 于晓辉,乔雨蒙,代旷宇,等.主余震序列作用下非线性单自由度体系的增量损伤分析[J].工程力学,2019,36(3):121-130.
YU Xiaohui,QIAO Yumeng,DAI Kuangyu,et al.Incremental damage analysis of nonlinear single-degree-freedom systems subjected to mainshock-aftershock earthquake sequences[J].Engineering Mechanics,2019,36(3):121-130.
[9] JEON J S,DESROCHES R,LOWES L N,et al.Framework of aftershock fragility assessment case studies: Older California reinforced concrete building frames[J].Earthquake Engineering and Structural Dynamics,2015,44(15):2617-2636.
[10]GODA K,SALAMI M R.Inelastic seismic demand estimation of wood-frame houses subjected to mainshock-aftershock sequences[J].Bulletin of Earthquake Engineering,2014,12(2):855-874.
[11]夏贇.基于整体损伤耗能的砌体结构主余震易损性分析[D].南昌:南昌大学,2023.
XIA Yun.Mainshock-Aftershock Vulnerability Analysis of Masonry Structure Based on Overall Damage Energy Dissipation[D].Nanchang:Nanchang University,2023.
[12]JGJ 99—2015,高层民用建筑钢结构技术规程[S].
[13]GB 50011—2010,建筑抗震设计规范[S].
[14]李佳琦.带竖向连杆的偏心支撑钢框架结构设计方法及抗震性能研究[D].石家庄:河北科技大学,2022.
LI Jiaqi.Research on the Design Method and Seismic Performance of Eccentric Braced Steel Frame Structure with Vertical Connecting Rods[D].Shijiazhuang:Hebei University of Science and Technology,2022.
[15]ASKARIANI S S,GARIVANI S,AGHAKOUCHAK A A.Application of slit link beam in eccentrically braced frames[J].Journal of Constructional Steel Research,2020.DOI:10.1016/j.jcsr.2020.106094.
[16]于晓辉,吕大刚,肖寒.主余震序列型地震动的增量损伤谱研究[J].工程力学,2017,34(3):47-53.
YU Xiaohui,LYU Dagang,XIAO Han.Study on incremental damage spectrum of main aftershock sequence type ground shaking[J].Engineering Mechanics,2017,34(3):47-53.
[17]李钱,吴轶,VINCENT L,等. 基于能量及损伤的主余震地震动对超限高层结构抗震性能影响研究[J]. 建筑结构, 2016, 46(9):42-47.
LI Qian, WU Yi, VINCENT L,et al.Study on the effects of main aftershock ground motions on seismic performance of high-rise structures beyond the code-specification based on energy and damage[J].Building Structure, 2016, 46(9):42-47.
[18]陶静.主余震序列作用下SDOF体系的增量损伤与抗倒塌能力研究[D].哈尔滨:哈尔滨工业大学,2016.
TAO Jing.Research on Incremental Damage and Collapse Resistance of SDOF System Under the Action of Main Aftershock Sequence[D].Harbin:Harbin Institute of Technology,2016.
[19]朱凯铭,郭玉荣.主余震序列作用下屈曲约束支撑框架易损性分析[J].结构工程师,2019,35(6):109-115.
ZHU Kaiming,GUO Yurong.Collapse fragility analysis of the buckling-restrained braced frame subjected to mainshock-aftershock sequences[J].Structural Engineers,2019,35(6):109-115.
[20]王伟,胡书领,邹超.基于增量动力分析的梁贯通式支撑钢框架地震易损性研究[J].建筑结构学报,2021,42(4):42-49.
WANG Wei,HU Shuling,ZOU Chao.Seismic fragility analysis of beam-through steel braced frames based on IDA method[J].Journal of Building Structures,2021,42(4):42-49.
[21]徐强,谭维佳,李文阳,等.考虑梁端耗能能力影响的钢框架结构易损性分析[J].世界地震工程,2020,36(3):109-115.
XU Qiang,TAN Weijia,LI Wenyang,et al.Vulnerability analysis of steel frame structures considering energy dissipation capacity of beam end[J].World Earthquake Engineering,2020,36(3):109-115.
[22]齐永胜,冯宁宁,贺芸.FEMA P695抗地震倒塌性能评估体系中CMR指标的调整[J].工程抗震与加固改造,2018,40(2):87-94.
QI Yongsheng,FENG Ningning,HE Yun.Adjustment of CMR index in FEMA P695 assessment system of seismic collapse[J].Earthquake Resistant Engineeringand Retrofitting,2018,40(2):87-94.
[23]ATC-63,Quantification of Building Seismic Performance Factors[S].
[24]单文臣.支撑巨型框架-核心筒结构体系的抗震设计及其自动优化方法[D].重庆:重庆大学,2021.
SHAN Wenchen.Seismic Design of Braced Giant Frame-Core Structure System and Its Automatic Optimization Method[D].Chongqing:Chongqing University,2021.

