NI-HTS线圈不同波形电流自场交流损耗的计算

摘 要：针对无绝缘高温超导线圈在交流传输和减小屏蔽电流采用的电流扫描反转等各种传输波形引起的自场交流损耗问题，基于E-J幂指数模型，提出采用磁矢势A和电流矢势T的T-A方法中的均质化模型方法，模拟计算传输电流、频率和n值对无绝缘高温超导饼式线圈的电流密度分布和传输交流损耗的影响。定量计算了双饼线圈中方波、锯齿波和正弦波的瞬时交流损耗；采用等效电路模型模拟分析了充/放电速率对无绝缘高温超导线圈匝间电流分布的影响。结果表明：在几百至几千赫兹时，无绝缘线圈的交流损耗随频率的增加而增加；受线圈匝间电流径向流动的影响，无绝缘线圈快速充电初期可出现局部环向电流反向，急速放电初期产生局部环向电流增加的情况。所得结果可以为无绝缘高温超导线圈的稳定性和交流损耗研究提供一定的理论参考。

关键词：超导物理学；高温超导磁体；无绝缘线圈；REBCO；交流损耗

中图分类号：O511+.9

文献标识码：A

DOI：10.7535/hbkd.2024yx05002

AC loss calculation in self-field of NI-HTS

coil carrying different transport currents

ZHAO Mingfei1，2， CUI Yingmin1，2， LI Qi1，2

（1.School of Mathematical and Physical Science， North China Electric Power University， Baoding， Hebei 071003， China;

2.Hebei Key Laboratory of Physics and Energy Technology， Baoding， Hebei 071003， China）

Abstract：To solve the problems of the AC loss in self-field for no-insulation （NI） HTS coils carrying different currentsLvdKdyMK/OrU91wvCFxSUV6N3r1ZYzUAZQe855YsHZs=， such as AC transport current， the current scanning inverse in order to decrease the screening current， and so on， by using the T-A homogenization model based on the E-J power law， the effects of the transport current， frequency， and the n-value on the magnetic flux density and AC loss of NI-HTS pancack coils were simulated. The instantaneous AC losses of square wave， sawtooth wave， and sinusoidal wave for double-pancake coil were simulated quantitatively. The effects of charging and discharging ramping rates on the current distribution were also discussed by using partial element equivalent circuit （PEEC）. The results show that the AC losses increase with the increase of frequency from several hundred to kilo Hz. Due to the transfer of the radial current within coil’s turns， some inverse azimuthal currents may appear in the NI-HTS coil in the early charging period， and some of the azimuthal currents may increase during short discharging period for the same reason. The simulation work can provide some theoretical references for the studies of the stability and AC loss for NI-HTS pancake coils.

Keywords：superconductingphysics；high-temperature superconducting magnet；no-insulation coil；REBCO；AC losses

超导技术是当今世界众多国家都比较关注的一项前沿科学技术，也纳入到中国第1个十年重点发展纲领《中国制造2025》中。由稀土（rare earth，Re）、钡（Ba）、铜（Cu）和氧（O）元素形成的二代的高温超导材料REBCO，已被广泛用于中/高场超导磁体、高工程电流密度传输电缆、超导磁储能（superconducting magnetic energy storage， SMES）等工程技术领域中[1-5]。近十几年，无绝缘（no-insulation， NI）高温超导 （high-temperature superconducting，HTS）线圈以其优越的热稳定性和“自保护”性能引起众多学者的研究兴趣[6-8]。2019年，美国国家高磁场实验室将 REBCO 带材绕制的无绝缘磁体内插于电阻式磁体中，产生了45.5 T的磁场[9]。同年，中国科学院电工研究所采用内插无绝缘REBCO线圈和低温超导线圈，成功研制出中心磁场高达32.35 T的全超导磁体[10]。当前对于无绝缘超导线圈研究，多基于磁体在正常运行状况下进行的直流和交流特性分析，常用方法有H公式[11-12]、T-A公式[13-14]，和A-H模型[15-16] 等。然而在实际问题中，超导磁体也会面临特殊情况：例如在中-高场中，磁体线圈受屏蔽电流的影响，可能需要电流扫描反转以减小屏蔽电流对中心磁场漂移的影响[17]；无绝缘HTS线圈在极端失稳情况下，可能面临毫秒级的失超过程等，目前对一些特殊情况下的无绝缘线圈的行为研究还有不足。

本文基于E-J模型，主要采用电流T-A法，对高温超导线圈中传输电流的磁通密度分布以及传输损耗进行二维计算，模拟研究了无绝缘单饼线圈传输电流幅值、频率和幂指数n对线圈内层电流密度分布和交流损耗的影响；研究了双饼线圈中不同电流波形的瞬时交流损耗和归一化电流密度的分布；利用等效电路模型讨论了较高充/放电速率对无绝缘HTS线圈稳定性的影响。

1 二维轴对称T-A模型

T-A方法用来计算二代高温超导带材制成的带堆和线圈的电磁特性已被广泛采用。在超导层中进行电流矢势T的建模计算和在整个空间系统中进行磁矢势A的耦合建模计算。在超导区求解的状态变量是电流矢量T，它由电流密度J的旋度来定义：

×T=J。（1）

电场和电流密度J可以表示为幂指数模型：

E=ρJ=E0（JJc（B））（|J|Jc（B））n-1 。（2）

临界电流密度Jc由修正的Kim关系式［18］定义，电流密度J只有φ分量，

Jc（B）=Jc0

（1+k2B2∥+B2⊥B0）α，（3）

×（ρ×T）=-Bt，（4）

式中：ρ，T，B和J分别是等效电阻率、电流矢势、施加的磁场和电流密度。在二维轴对称模型中上述方程可以简化为

z（ρTrz）=-Brt 。（5）

电流矢势T只有垂直于超导层方向的分量，传输电流I用狄利克雷边界表示，满足：

I=（T1-T2）δ，（6）

式中：T1，T2分别为超导带材上端和下端的电流矢势；δ为超导层厚度。

均质化模型和多尺度模型［19-21］是基于T-A公式的2种改进方法。与T-A全模型相比，这些方法使用了更少的资源，同时获得了类似的磁滞损耗以及电流密度和磁场分布的精度。二维轴对称模型中，电流密度的φ分量定义为Jφ=

Trz。将超导带中的电流密度

Jφ乘以超导层的厚度δ，以获得表面电流密度K=Jφ·δ，该表面电流密度通过边界条件施加到线圈中。

m×（H1-H2）=K，（7）

式中：m为垂直超导带方向的单位矢量；H1和H2分别是层上方和下方的磁场强度矢量。

缩放后的电流密度定义为Js=δΛJφ，其中δ 是带材的厚度，Λ是计算单元的厚度，Js满足如下公式：

2Aφ=-μ0（σ0Eφ+Js） 。（8）

交流损耗计算公式如下：

Q=2T∫TT/2

dt∫ΩE·JdΩ，（9）

式中：T为电流变化周期；Ω为超导体计算区域。

本文对3个小型无绝缘HTS饼式线圈进行了模拟计算，相关参数如表1所示。考虑到线圈模拟运行电流在25～40 A，小于临界电流

Ic，HTS磁体处于较稳定的正常运行状态，因此计算中匝间接触电阻率70 μΩ·cm2保持不变［22］。

2 计算结果与讨论

2.1 单饼线圈1的交流损耗和电流密度分布

n值反映超导体从超导态向正常态转变的快慢程度。图1 a）给出了线圈1在1个周期内正弦交变传输电流下瞬时交流损耗与n值的关系曲线，其中I=0.5Icsin（2πft）， f=50 Hz。比较发现：图1 a）显示n值较大时，交流损耗峰值会略增大一些。图1 b）表明交变电流下，超导带边缘的电流密度大于中心值，n值对单饼线圈宽度边缘的电流密度影响略大，带宽中部电流密度较低，受n值影响不大。

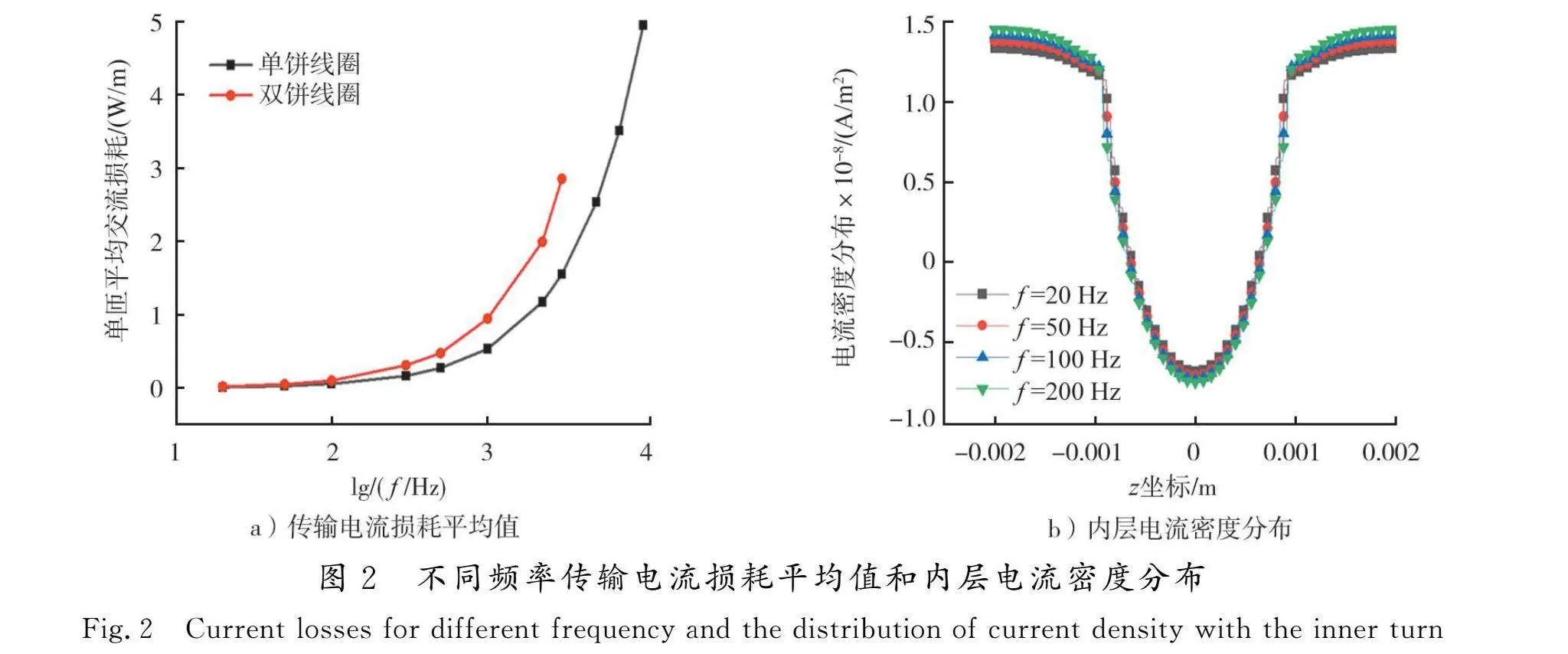
无绝缘线圈1在不同频率下的单匝平均传输损耗如图2 a）所示，当传输电流频率（f）较高时，由于金属基材中的涡流损耗增加较快，导致了线圈平均传输损耗随着频率的增加而增加，这与实验结果［23］相吻合。图2 b）为传输电流峰值时线圈最内匝电流密度分布，传输电流频率对线圈宽度边缘电流密度影响也相对较大，边缘电流密度随着频率的增加而增大，线圈内部电流密度受频率影响则相对较小。

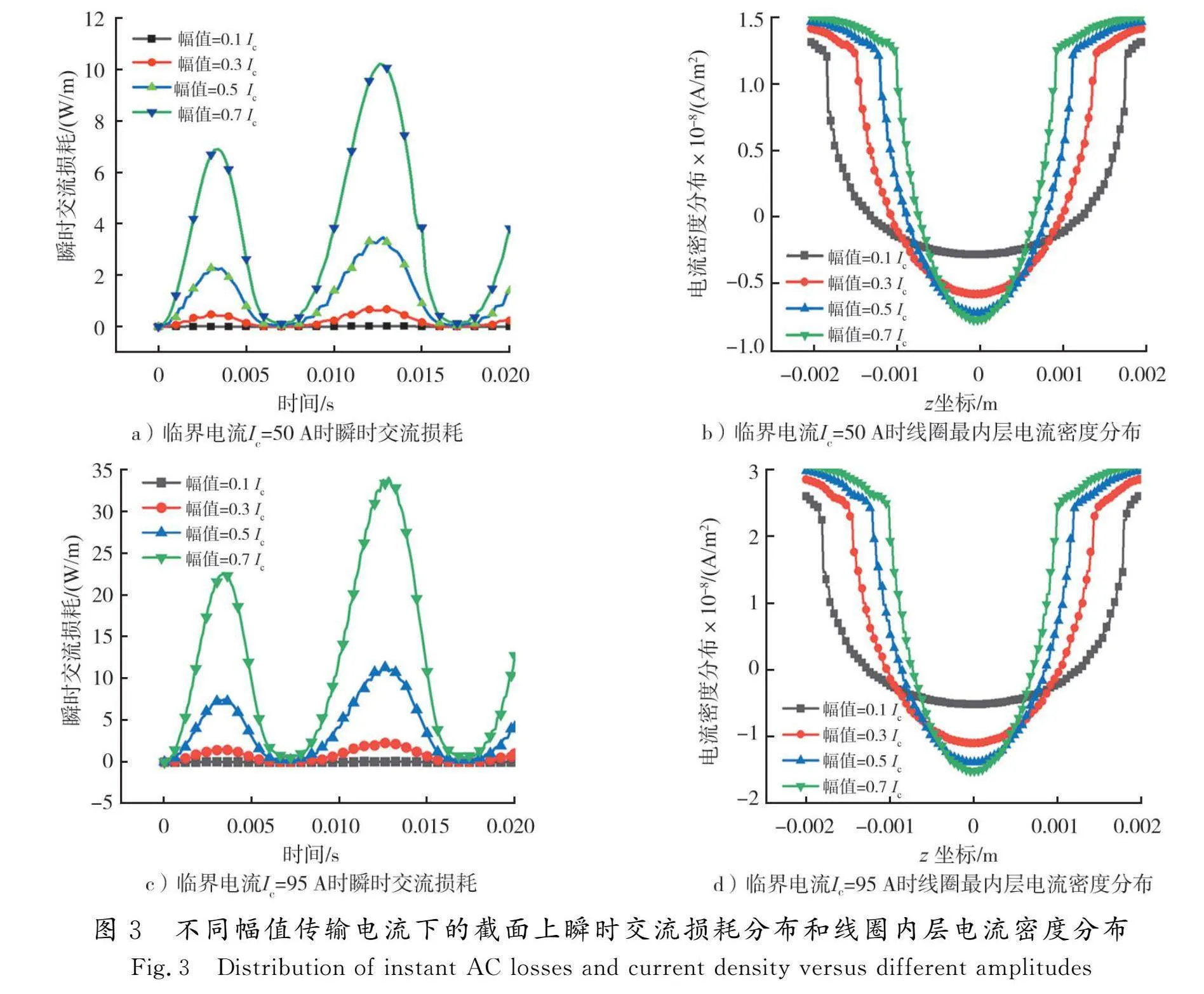
图3模拟线圈1不同幅值的50 Hz交变电流对瞬时交流损耗和最内层电流密度的影响，其中图3 a）—b）的线圈自场临界电流Ic@50 A［22］，图3 c）—d）为自场临界电流Ic@95 A的同尺寸线圈。由图可知，瞬时传输损耗随着电流幅值的增加而增加，带材电流密度呈对称分布。线圈带材两端电流密度较大，中部电流密度较低。随着传输电流的增加，线圈端部的电流密度的增加缓慢，传输电流逐渐从线圈带材端部向中部渗透。图3 b）和图3 d）表明：线圈最内层带材中部有负值的反方向电流（最外层结果相同）。分析认为， 0～0005 s是传输电流上升的1/4周期，受自场增加的影响，超导线圈最内/外层会产生反向的感应屏蔽电流，因为传输电流集中分布在超导带两端，超导带中间传输电流较低，所以体现出负值的反向感应电流。图3 a）—d）对比表明：相同的归一化交变传输电流下，无绝缘HTS线圈带材的传输电流密度与临界电流成正比。

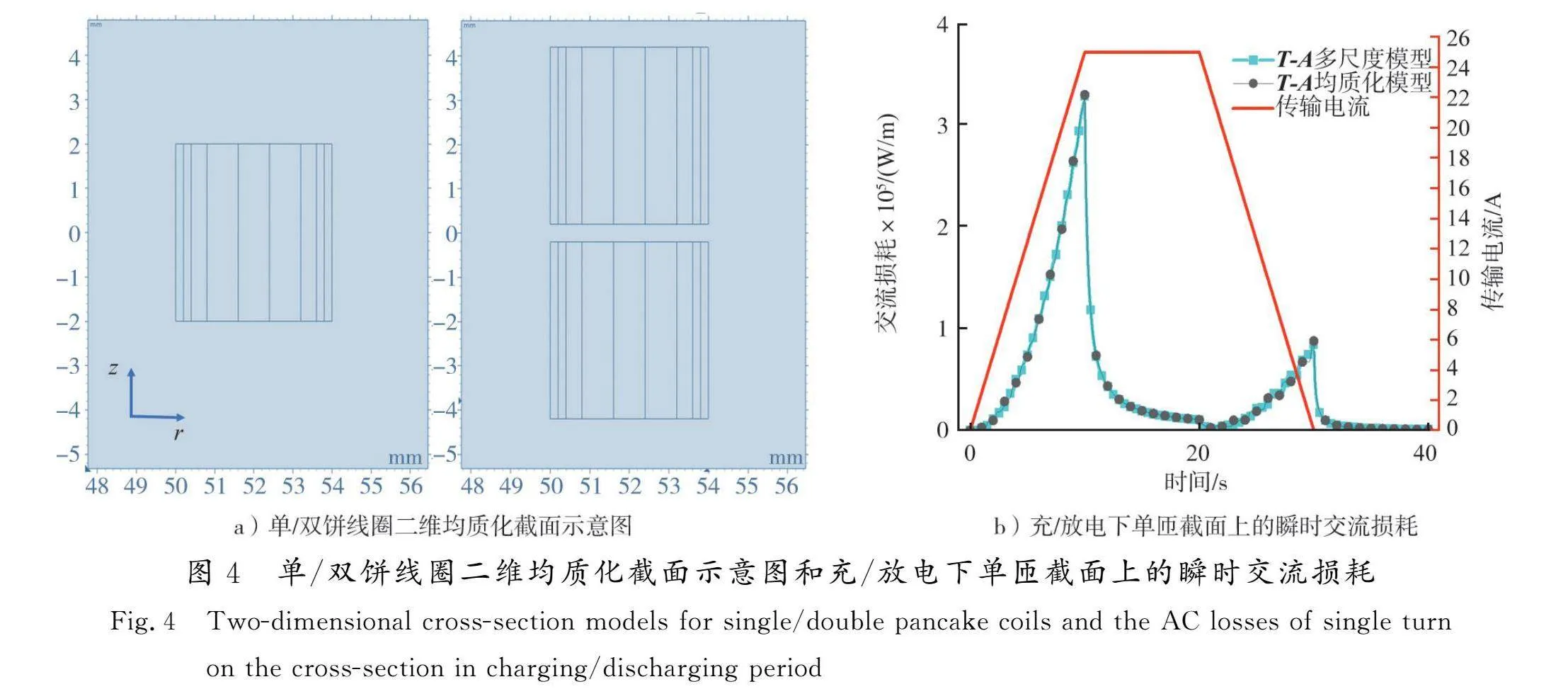
单/双饼线圈的二维均质化截面模型如图4 a）所示，线圈1的单匝截面上的瞬时交流损耗如图4 b）所示。线圈1以2.5 A/s速率充电10 s后，电流保持25 A恒定10 s后，以2.5 A/s放电10 s至0，整个过程传输损耗随传输电流的变化如图4 b）所示。

2.2 双饼线圈仿真模拟

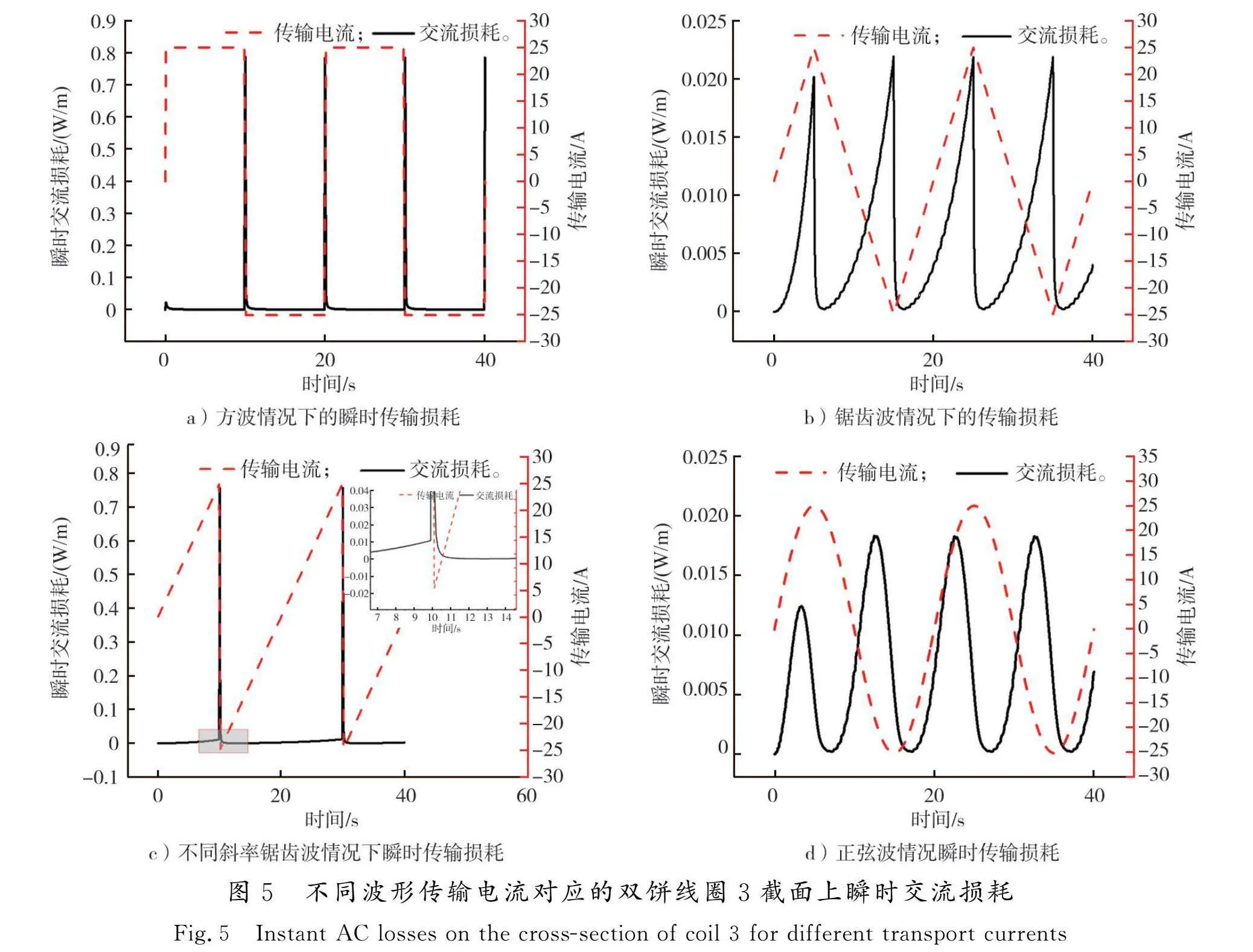
双饼线圈3为2个相同匝数和尺寸的无绝缘单饼线圈叠加组成，两饼间距0.4 mm。给双饼线圈分别通入方波，不同励磁速率（5 A/s和2.5 A/s）的锯齿波以及正弦波4种波形传输电流（峰值均为25 A，周期均为20 s），对比线圈交流损耗、磁通密度以及归一化电流密度分布规律，结果如图5所示。

给双饼线圈通入方波传输电流时，根据图5 a）可以看到，交流损耗在传输电流平稳时为0。因为线圈在电流幅值不变时，磁场强度和方向保持不变，无磁通运动，损耗为0。当传输电流变化时，线圈内磁通发生实时变化，引起传输损耗变化。

对比图5 b）与图5 c），当传输电流励磁速度变大但电流幅值不变时，在传输电流变化速率最大时损耗会出现峰值，这是由于传输电流瞬间变小，会引起线圈内磁通发生变化，导致交流损耗瞬间变大。图5 c）中线圈在0～10 s励磁过程中，上升速率为2.5 A/s，把图5 c）局部放大后，第10 s的瞬时交流损耗值为0.01 W/m；图5 b）0～5 s励磁过程中，上升速率为5 A/s，第5 s瞬时交流损耗值为0.02 W/m，对比可得：线圈截面的瞬时交流损耗随电流励磁速率的增加有上升趋势。对比图5 b）与图5 d）可知，传输电流幅值周期一定时，正弦波的交流损耗峰值比锯齿波较小一些，但相差不大，这是因为正弦波传输电流的变化率比锯齿波小，因此引起的磁通运动变化较小，由于交流损耗是磁通运动引起的，所以正弦波传输电流交流损耗峰值较小，并且由于瞬态效应，第1个峰值都较小。

双饼线圈的方波传输电流下的磁通密度和归一化电流分布如图6所示。当传输电流不变时，线圈内磁通密度分布也不变，当电流瞬间变小，会引起磁通密度减小。磁通变化，产生屏蔽电流，中间深蓝色区域磁通密度较小。从图6 b）中可以看出，屏蔽电流分布也是对称的。

2.3 充/放电速率与无绝缘线圈的电流分布

无绝缘线圈在较低的充放电速率（0.1～1 A/s）和正常恒流工作模式时，高温超导线圈环向电阻为0，径向接触电阻高于环向电阻，电流沿环向流动。当充放电速率较高时，环向电流受电感阻碍的影响，可能出现部分电流向径向转移。根据PEEC复杂电路模型［24-27］，把无绝缘超导线圈每一匝平均化分为若干个计算单元（divs），根据基尔霍夫定律， 线圈中每个单元满足电流方程如下［28］：

［C1］{Iθ（t）}={C2} ，（10）

式中：矢量 {Iθ（t）} 由每个单元的环向电流作为数组元素（随时间变化）组成；矩阵[C1]包含单元内REBCO可变电阻、超导基材电阻、匝间接触电阻、单元自感和单元间互感系数；矢量{C2}包含接触电阻、基材电阻、单元自感和互感系数、随时间变化的总传输电流、前一个时间步长的环向电流变化

Iθ（t-Δt）和电流变化所引起的感应电动势。求解式（10）可得无缘线圈每个单元的电流。本文计算了充/放电速率分别为 0.1 A/ms和4 A/ms 情况下，无绝缘超导单饼线圈2中的电流变化，其中模拟时间步长h=1×10-5 s。

图7为模型中采用Nd=1 div/匝的计算结果，蓝色线为总传输电流，橙色线为线圈每匝的环向电流。图7 a）显示，0.4 s时总电流达到40 A，线圈中环向电流约为20 A；图7 b）显示，0.4 s时环向电流约为33 A。对比表明，充放电速率较高时，励磁速率相应也较快。

为了更明确快充/放电速率对径向电流的影响，本文采用充放电速率为4 A/ms且更为细致的每匝多单元PEEC模型计算。图8 a）为4 divs/匝的环向电流分布计算结果。c1表明，快速充电时环向局部出现反向（负值）电流，这是因为快速充电引起径向电流的双向流动（沿两侧反方向逐渐汇入环向电流）导致，反向电流仅出现在快速充电的初始时间段内，当环向电流逐步增加时，反向电流则会淹没在正方向环向电流中。s66ciSuR5S0Y6Wo26Blryw==同理，无绝缘线圈快速放电时，由于受径向电流双向流动的影响，环向电流出现短时间局部大于传输电流值的现象（如c2所示）。图8 b）为线圈充电过程中t=6 ms时，无绝缘线圈2的电流瞬时分布图。计算采用Nd=36 div/匝，输入电流端坐标为（15.0 mm，0°），输出电流端为（15.9 mm，360°）。如图8 b）所示，充电和放电端的环向电流显示约为23 A，径向电流显示约为1 A，总输运电流达到24 A@6 ms。对比径向电流图可知，在充电过程中，无绝缘线圈电流输入和输出端附近匝间，出现了局部环向电流反向的现象（环向电流图的深蓝色区域）。可以理解为径向电流沿两个相反的方向转移到环向电流，该结果与图8 a）一致。无绝缘高温超导线圈在高充放电速率下，出现短时间的环向和径向电流不均匀性，在高场下可能导致线圈应力和应变不均匀，严重的可能诱发失超，影响磁体稳定运行。

3 结 语

本文采用T-A模型和等效电路模型，对3个小型无绝缘高温超导线圈进行了模拟计算。研究了不同n值、频率和临界电流密度对单饼线圈交流损耗和电流密度分布的影响，双饼线圈在不同传输波形下的交流损耗和磁通密度分布，以及充/放电速率对匝间电流分布的影响。交变传输电流主要沿线圈带宽两侧分布，中部则较多体现为屏蔽电流；频率较高时，受金属基材涡流损耗增加的影响，线圈的交流损耗随着频率和幅值的增加而增加；无绝缘HTS线圈在快速充/放电时，电流沿径向流动现象较为突出，短时间内可能出现局部环向电流反向或环向电流瞬时增大等现象。电流的不均匀分布，在高场下将导致线圈局部受力不均匀，从而可能对磁体的稳定运行产生潜在影响。本文可以为高温超导线圈的交流损耗和磁体稳定性的研究提供一定的理论参考。

以上结论主要基于仿真结果，后续工作将对无绝缘线圈开展实验测试，研究实际工况下无绝缘线圈的交流损耗以及其失超和恢复特性。

参考文献/References：

[1] JO J H，RYU Y G，CHOE Y.Simulation on modified multi-surface levitation structure of superconducting magnetic bearing for flywheel energy storage system by H-formulation and Taguchi method[J].Physica C：Superconductivity and Its Applications，2023. DOI：10.1016/j.physc.2023.1354305.

[2] SAID S M，ABDEL-SALAM M，NAYEL M，et al.Optimal design and cost of superconducting magnetic energy storage for voltage sag mitigation in a real distribution network[J].Journal of Energy Storage，2023. DOI：10.1016/j.est.2023.108864.

[3] LI Wenxin，YANG Tianhui，LI Chao，et al.Exploration on the application of a new type of superconducting energy storage for regenerative braking in urban rail transit[J].Superconductor Science and Technology，2023.DOI：10.1088/1361-6668/acf902.

[4] RADU J，DUMITRU C.Design and numerical study o_{+OtcNNEnc2oNm6uOsjeF0g==}f magnetic energy storage in toroidal superconducting magnets made of YBCO and BSCCO[J].Magnetochemistry，2023. DOI：10.3390/magnetochemistry9100216.

[5] ESMAEILI M S，MEHRPOOYA M.Modeling and exergy analysis of an integrated cryogenic refrigeration system and superconducting magnetic energy storage[J].Journal of Energy Storage，2023.DOI：10.1016/j.est.2023.109033.

[6] WANG Kangshuai，WANG Qiuliang，ZHOU Benzhe，et al.Analysis of charging characteristics of a 500 MHz HTS-LTS series NMR magnet with an intra-layer no-insulation HTS layer-wound coil structure[J].Physica C：Superconductivity and Its Applications，2023. DOI：10.1016/j.physc.2023.1354372.

[7] KIM G Y，PARK J H，BNG J，et al.Investigation on nonuniform current density and shape deformation affecting the magnetic field performance of a saddle-shaped no-insulation HTS cosine-theta dipole magnet[J].Superconductor Science and Technology，2023. DOI： 10.1088/1361-6668/acdf8d.

[8] ZHONG Zhuoyan，WU Wei，LU Lu，et al.Time-variant magnetic field，voltage，and loss of no-insulation （NI） HTS magnet induced by dynamic resistance generation from external AC fields[J].Superconductor Science and Technology，2023. DOI： 10.1088/1361-6668/acbd6b.

[9] HAHN S，KIM K，KIM K，et al.45.5-tesla direct-current magnetic field generated with a high-temperature superconducting magnet[J].Nature，2019，570（7762）：496-499.

[10]LIU Jianhua，WANG Qiuliang，QIN Lang，et al.World record 3235-tesla direct-current magnetic field generated with whole superconductor magnet[J].Superconductor Science and Technology，2020，33（3）：1-5.

[11]YONG Huadong，WEI Dong，TANG Yunkai，et al.Numerical modelling of electromechanical coupling behaviors in HTS coil with implementation of H formulation in FE software[J].Superconductivity，2024. DOI：10.1016/j.supcon.2024.100097.

[12]YAN Yufan，QU Timing，GRILLI F.Numerical modeling of AC loss in HTS coated conductors and roebel cable using T-A formulation and comparison with H formulation[J].IEEE Access，2021，9：49649-49659.

[13]XU Xiaoyong，HUANG Zhen，LI Wan，et al.3D finite element modelling on racetrack coils using the homogeneous T-A formulation[J].Cryogenics，2021.DOI：10.1016/J.CRYOGENICS.2021.103366.

[14]VARGAS L C R，HUBER F，RIVA N，et al.3D homogenization of the T-A formulation for the analysis of coils with complex geometries[J].Superconductor Science and Technology，2022. DOI：10.1088/1361-6668/ac9932.

[15]SANTOS B M O，DIAS F J M，SASS F，et al.Simulation of superconducting machine with stacks of coated conductors using hybrid A-H formulation[J].IEEE Transactions on Applied Superconductivity，2020，30（6）：1-9.

[16]BORTOT L，AUCHMANN B，GARCIA I C，et al.A coupled A-H formulation for magneto-thermal transients in high-temperature superconducting magnets[J].IEEE Transactions on Applied Superconductivity，2020，30（5）：1-11.

[17]KIM Y G，CHOI Y H，YANG D G，et al.Study for reducing the screening Current-Induced field in a 10-MHz No-Insulation magnet using current sweep reversal method[J].IEEE Transactions on Applied Superconductivity，2015，25（3）：1-5.

[18]KIM Y，HEMPSTEAD C，STRNAD A.Magnetization and critical supercurrents[J].Physical Reviews Letters，1963. DOI：10.1103/PhysRev.129.528.

[19]WANG Yaning，JING Ze.Multiscale modelling and numerical homogenization of the coupled multiphysical behaviors of high-field high temperature superconducting magnets[J].Composite Structures，2023. DOI：10.1016/j.compstruct.2023.116863.

[20]JUAREZ E B，TRILLAUD F，ZERMENO V M，et al.Screening current-induced field and field drift study in HTS coils using T-A homogenous model[J].Journal of Physics：Conference Series，2020. DOI：10.1088/1742-6596/1559/1/012128.

[21]ZHANG Huiming，ZHANG Min，YUAN Weijia.An efficient 3D finite element method model based on the T-A formulation for superconducting coated conductors[J].Superconductor Science and Technology，2017. DOI：10.1088/1361-6DKpTRYC7i051xSKOtU7KVg==668/30/2/024005.

[22]WANG Xudong，HAHN S，KIM Y，et al.Turn-to-turn contact characteristics for an equivalent circuit model of no-insulation ReBCO pancake coil[J].Superconductor Science and Technology，2013. DOI： 10.1088/0953-2048/26/3/035012.

[23]GUO Shuqiang，REN Li，LI Xin，et al.The relationship between AC loss of YBCO superconducting coil and current waveform，amplitude，frequency and temperature[J].Physica C：Superconductivity and Its Applications，2021. DOI：10.1016/j.physc.2021.1353839.

[24]HAHN S，PARK D K，BASCUN J，et al.HTS pancake coils without turn-to-turn insulation[J].IEEE Transactions on Applied Superconductivity，2011. DOI： 10.1109/tasc.2010.2093492.

[25]ITOH R，OGA Y，NOGUCHI S，et al.Screening current simulation inside YBCO tape in charging YBCO magnet[J].IEEE Transactions on Applied Superconductivity，2013. DOI：10.1109/tasc.2012.2236373.

[26]WANG Y，SONG H，XU D，et al.An equivalent circuit grid model for no-insulation HTS pancake coils[J].Superconductor Science and Technology，2015. DOI： 10.1088/0953-2048/28/4/045017.

[27]LIU Yingzhen，OU Jing，GYURAKI R，et al.Study of contact resistivity of a no-insulation superconducting coil[J].Superconductivity Science Technology，2021. DOI： 10.1088/1361-6668/abd14d.

[28]SUETOMI Y，YOSHIDA T，TAKAHASHI S，et al.Quench and self-protecting behaviour of an intra-layer no-insulation （LNI） REBCO coil at 314 T[J].Superconductor Science and Technology，2021. DOI： 10.1088/1361-6668/abf54e.