基于分数阶的反激变换器精细建模

摘 要：针对传统建模方法无法更加精确地描述反激变换器真实特性的问题，利用分数阶微积分和状态空间平均法，对工作在电感电流断续模式下的分数阶反激变换器进行建模与分析。建立了电感电流断续模式下分数阶反激变换器的平均状态模型，得到其直流平衡点和小信号传递函数，对比其与整数阶数学模型的差异；在Simulink中搭建分数阶反激变换器的状态空间模型和电路仿真模型，以及构造分数阶反激变换器的实物实验电路；通过状态空间模型、电路模型仿真和实验结果三者对比验证所推导的分数阶模型的正确性。结果表明，分数阶数学模型能反映电感电容阶数的变化，进行理论分析能更符合该变换器的实际工作情况。将分数阶微积分理论与状态空间平均法结合，可建立更为精确的反激变换器数学模型，为其他变换器的建模提供了参考。

关键词：电力电子技术；电感电流断续模式；分数阶反激变换器；数值仿真；实物电路

中图分类号：TM46

文献标识码：A

DOI：10.7535/hbkd.2024yx05001

Fine modeling of flyback converter based on fractional order

YANG Peng1，2， LI Qian1， SHI Shanzhe2， FU Yinan3， LIU Yuzhi3

（1.State Grid Hebei Marketing Service Center Company Limited， Shijiazhuang， Hebei 050000， China;

2.State Grid Hebei Electric Power Research Institute Company Limited， Shijiazhuang， Hebei 050000， China;

3.School of Electrical and Electronic Engineering， Shijiazhuang Tiedao University， Shijiazhuang， Hebei 050043， China）

Abstract：Aiming at the problem that the traditional modeling methods cannot describe the real characteristics of flyback converters more accurately， the average state model of the fractional-order flyback converter operating in the intermittent inductance current mode was established by using fractional-order calculus and state space average method. The DC equilibrium point and small signal transfer function were obtained， and the difference between the model and the integer order mathematical model was compared. The state space model and circuit simulation model of fractional-order flyback converter were built in Simulink， and the experimental circuit of fractional-order flyback converter was constructed. The state space model， circuit model simulation and experimental results were compared to prove the correctness of the fractional-order model. The results show that the fractional order mathematical model can reflect the change of the order of inductance and capacitance， and the theoretical analysis is better consistent with the actual operation of the converter. A more accurate mathematical model of flyback converter can be established by combining fractional calculus theory with state space average method， which provides a reference for the modeling of other converters.

Keywords：power electronic technology; intermittent inductance current mode; fractional-order flyback converter; numerical simulation; physical circuitry

在开关电源中反激变换器应用最为广泛，其拓扑结构简单，具有转换效率高、体积小、不需要输出滤波电感等各种优点[1]。工作于电感电流断续模式下的反激变换器，其原边励磁电感更小、电压比更高，同时具有更好的抗电压波动和负载突变能力[2]。在反激变换器中电感、电容是常见的储能元件，研究表明这些元件本质上是分数阶的。传统模型中元件的整数阶模型常常被用于变换器的建模与分析，这忽略了元件分数阶的特性，可能会得出错误的结果[3]。以SiC和GaN为代表的第3代半导体功率器件具有更高的开关速度，因此对于反激变换器的数学模型的频率响应要求更高。传统模型可能无法准确描述高频下器件的动态特性，因此需要更为精确的模型以考虑更高的开关频率。

文献[4]对工作在电感电流连续模式下的反激变换器进行分数阶建模，利用开关网络平均法，得到了反激变换器的直流平衡点和交流小信号传递函数，并利用PSIM仿真验证了分数阶模型的准确性。文献[5]利用开关网络平均法对分数阶反激变换器工作在电感电流断续模式下时进行了分析，但其电容电感使用的是整数阶特性计算，并未采用分数阶的计算。文献[6]利用小信号交流分析对工作在电感电流断续模式下的整数阶反激变换器进行建模，但依旧没有考虑电容电感为分数阶这一特性。文献[7]将反激变换器负载模型等效为电阻和电流源的并联，利用状态空间平均法建立整数阶电感电流断续模式下反激变换器的小信号模型，并推导了各个交流小信号传递函数，但其也没有考虑到电容电感为分数阶的特性。

本文针对工作在电感电流断续模式下的分数阶反激变换器缺乏能够描述其精细数学模型的问题，从分数阶电容和电感出发，利用分数阶微积分原理和状态空间平均法，建立其分数阶模型，推导得出静态工作点和小信号交流传递函数并进行理论分析，并将其与整数阶模型进行对比。最后，在Matlab/Simulink中搭建工作在电感电流断续模式下的分数阶反激变换器的数值仿真模型，构建了实物电路，将实验结果与理论计算、电路仿真结果通过绘图进行直观对比，验证了分数阶理论分析以及建模的准确性。

1 反激变换器的分数阶区间数学建模与分析

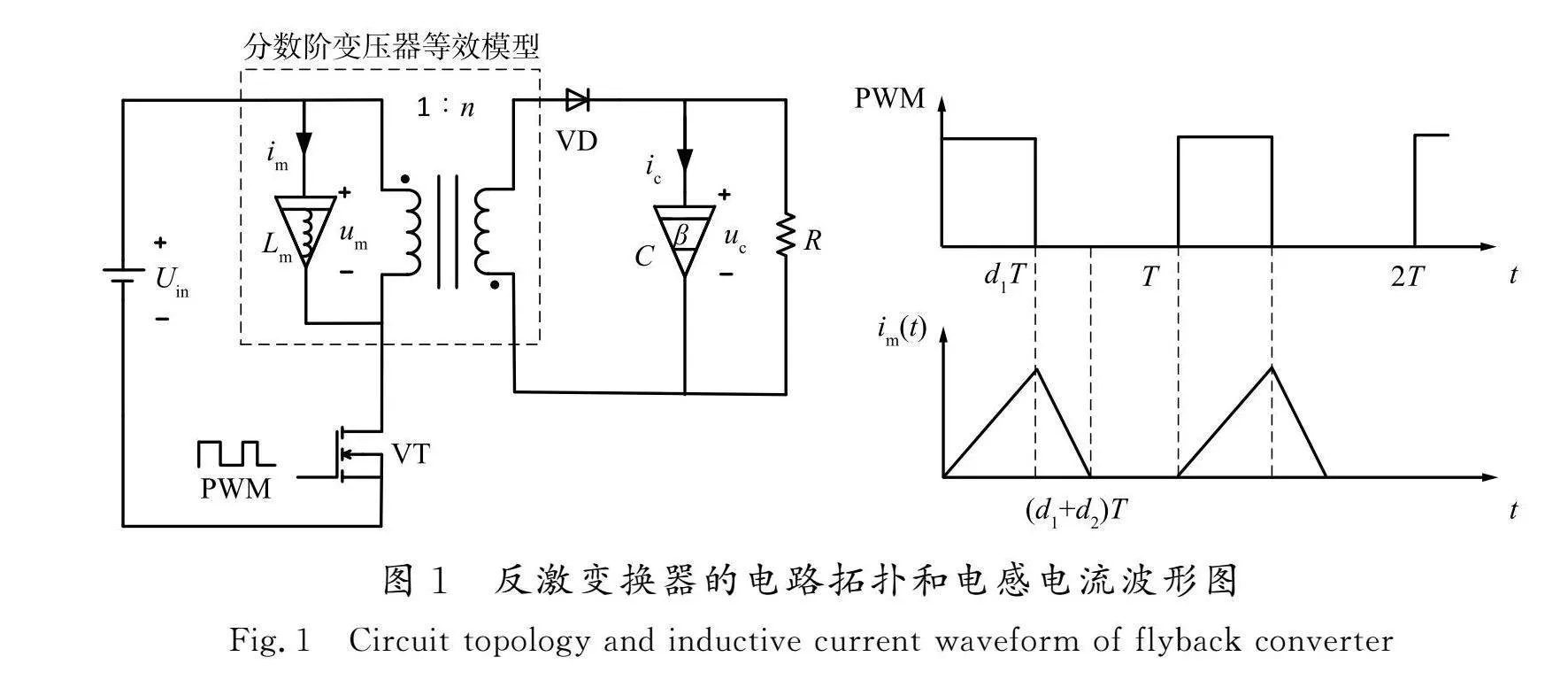
反激变换器电路拓扑图和在PWM周期性开关脉冲调制下的电感电流波形如图1所示，其中反激变换器的变压器等效为励磁电感与理想变压的并联形式，PWM开关周期为T。

当反激变换器工作在电感电流断续模式下时， 其有3种工作模态。

1）在0<t≤d1T时，PWM为高电平，VT导通，VD承受反向电压关断， 输入电压施加到分数阶励磁电感两端，开始储能，电感电流上升，同时分数阶电容向负载供电，这一工作状态称为工作模态1， 持续时间为d1T，其状态方程为

dαimdtα=uinLm，

dβucdtβ=-ucRC。（1）

2）在d1T<t≤（d1+d2）T时，PWM为低电平， VT关断，VD承受正向电压导通， 分数阶励磁电感通过理想变压器和VD向分数阶电容及负载供电，在（d1+d2）T时电感电流降为0，这一工作状态称为工作模态2， 持续时间为d2T， 其状态方程为

dαimdtα=-ucnLm，

dβucdtβ=imnC-ucRC。（2）

3）在（d1+d2）T<t≤T时，PWM为低电平， 励磁电感电流为零，VT关断，VD关断，分数阶电容向负载供电，这一工作状态称为工作模态3，持续时间为（1-d1-d2）T，其状态方程为

dαimdtα=0，

dβucdtβ=-ucRC。（3）

上述状态方程中：uin为输入电压;im为电感电流;uc为输出电压;d1为占空比;d2为电感电流从最大值下降到零的时间与周期的比值;Lm为分数阶电感;C为分数阶电容;α为分数阶电感的阶数，0<α<1；β为分数阶电容阶数，0<β<1。

2 反激变换器分数阶状态平均模型的建立与分析

2.1 反激变换器分数阶状态平均模型的建立

由式（1）—式（3）可以得出，工作于电感电流断续模式下的分数阶反激变换器其分数阶状态方程会被电感阶数α及电容阶数β所影响。

结合式（1）—式（3），利用状态空间平均法， 得出其状态平均模型为

dα〈im〉dtα=d1〈uin〉Lm-d2〈uc〉Lm，

b62GOI1jwh+OA72wK9Ckow==dβ〈uin〉dtβ=d2〈im〉C-〈uc〉RC，

（4）

式中：〈im〉、〈uin〉、〈uc〉、d1、d2分别为其相应量在一个开关周期内的平均值，可将其分解为交流分量和直流分量相加，其中交流分量分别为i′m、u′in、u′c、d′1、d′2，直流分量分别为Im、Uin、Uc、D1、D2，如式（5）所示；同时|i′m|Im，|u′in|Uin，|u′c|Uc，

|d′1|D1，|d′2|D2。

〈im〉=Im+i′m，

〈uin〉=Uin+u′in，

〈uc〉=Uc+u′c，

d1=D1+d′1，

d2=D2+d′2。（5）

2.2 反激变换器分数阶状态平均模型的分析

将式（5）代入式（4），忽略高阶小量，即令u′ind′1≈0，i′md′2≈0，u′cd′2≈0，可以得到

dα（Im+i′m）dtα=UinD1+Uind′1+D1u′inLm-UcD2+Ucd′2+D2u′cnLm，

dβ（Uc+u′c）dtβ=ImD2+Imd′2+D2i′mnC-Uc+u′cRC。（6）

将式（6）中的直流分量分离出来，可得

dαImdtα=D1UinLm-D2UcnLm，

dβUcdtβ=D2ImnC-UcRC。（7）

由分数阶Caputo微分性质可知，式（7）左侧为零，因此联立上下式可得系统的稳态工作点，即升压比M和电感电流直流分量Im。

M=UcUin=nD1D2，（8）

Im=nUcRD2。（9）

利用伏秒平衡原理，在一个开关周期内，当电感电流断续时的初始时刻以及终止时刻都为零，则可得该周期中电感电压平均值为零[8]：

〈um〉=0。（10）

利用分数阶电感的伏安关系， 有

dα〈im〉dtα=0。（11）

利用式（1）可得电感电流的平均值近似为

〈im〉=〈Uin〉（d1T）α2αLmΓ（α）。（12）

将式（5）代入式（12）中，忽略高阶小量，即（d′1）n≈0（n>2）和u′in（d1）n≈0（n≥1）有

Im+i′m=（D1T）α2LmαΓ（α）Uin+u′in+Uin

αd′1D1。（13）

对式（13）进行直流分量分离后有

Im=Uin（D1T）α2LmαΓ（α）。（14）

因此， 把式（14）代入式（8）和式（9）后， 有

D2=n2LmαΓ（α）D1Dα1TαR，（15）

Uc=UinDα+11TαR2LmαΓ（α）。（16）

由于电感电流在每个开关周期都是从零升到最大值，再在开关周期结束之前从最大值降为零，所以电感电流纹波等于电感电流最大值，可以用电感电流在（0，D1T）内的增加量求出，即式（1）求分数阶积分运算可得式（17），由此可见它也近似等于电感电流平均值Im的2倍。

Δim=im-max=Uin（D1T）αLmαΓ（α），（17）

式中Γ（α）为Gamma函数，定义为Γ（α）=∫∞0e-ttα-1dt。

由式（17）可以看出，电感电流纹波Δim和电感电流最大值im-max不仅与输入电压Uin、电感Lm、占空比D1以及开关周期T有关，还与电感的阶数α有关，且随着α的减小，电感电流最大值im-max和电感电流纹波Δim增大。且当α为整数1时，用整数阶模型所求的结果与式（17）一致。对于分数阶反激变换器，其断续导通模式条件与整数阶反激变换器类似，均应是电感电流的静态工作点要小于电感电流纹波的一半，即Im<Δim/2，电感的阶数α会影响变换器的工作模式。

2.3 反激变换器分数阶状态平均模型的分析

将式（6）中的交流分量分离出来，可得

dαi′mdtα=Uind′1+D1u′inLm-Ucd′2+D2u′cnLm，

dβu′cdtβ=Imd′2+D2i′mnC-u′cRC。（18）

根据式（5）和式（11）可进一步推得

dαi′mdtα=0。（19）

因此

d′2=nUind′1+nD1u′in-D2u′cUc。（20）

对式（13）进行交流分量分离后有

i′m=（D1T）α2LmαΓ（α）u′in+Uinαd′1D1。（21）

把d′2和i′m的表达式代入式（18）的第2个式子，得到表达式如下：

Guu（s）=u′c（s）u′in（s）d′1（s）=0=

D2（D1T）α2LmαΓ（α）nC+ImD1UcC

sβ+D2ImncUc+1RC，（22）

Gud1（s）=u′c（s）d′1（s）u′in（s）=0=

αUinD2（D1T）α2nLmαΓ（α）CD1+ImUin

UcC

sβ+D2ImncUc+1RC。（23）

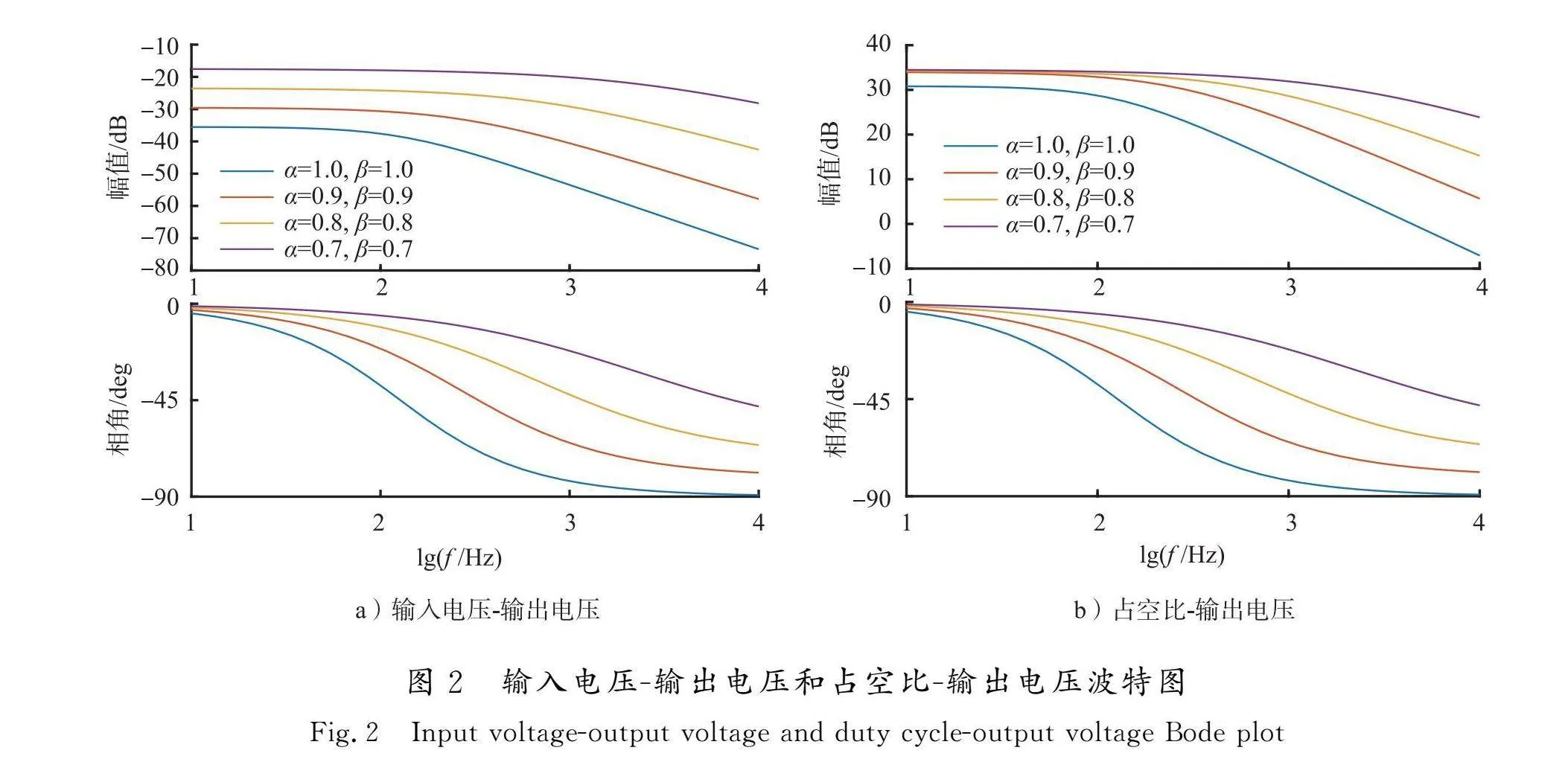
从式（23）可以看出，小信号传递函数Guu（s）和Gud（s）均受分数阶电感和电容的阶数α和β的影响。假设反激变换器系统参数为Uin=40 V、L=1 mH、C=1 mF、R=5 Ω，开关频率f=100 kHz、开关周期T=25 μs，则在Matlab中画出的输入-输出和占空比-输出2个传递函数在不同分数阶电感以及不同分数阶电容的阶数α和β情况下的波特图如图2所示。

由图2可看出，传递函数Guu（s）和Gud（s）的波特图随分数阶电感电容的阶次α和β变化较大，且当α和β较小时，其波特图与整数阶（α=β=1）相差较大，说明反激变换器的频域特性和分数阶电感电容的阶次α和β有密切的关系。当电感和电容的分数阶阶次α和β都为整数1时，式（22）和式（23）与文献[4]和文献[5]中的整数阶传递函数表达式相同，再次说明了分数阶理论的准确性。

综上，反激变换器工作在电感电流断续模式下的输出电压Uc、电感电流Im、电感电流从最大值下降到零的时间与周期的比值D2、电感电流纹波Δim、电感电流最大值im-max和小信号传递函数除了与其拓扑结构参数L、C、R大小有关之外，还受到分数阶电感电容的阶次α和β的影响。而电感电流断续模式下的反激变换器整数阶模型不随分数阶电感电容的阶数而变化，没有考虑到分数阶电感电容的阶次α和β的影响，可能最终得出不精确的结果。

3 仿 真

3.1 分数阶电感和电容的等效电路模型

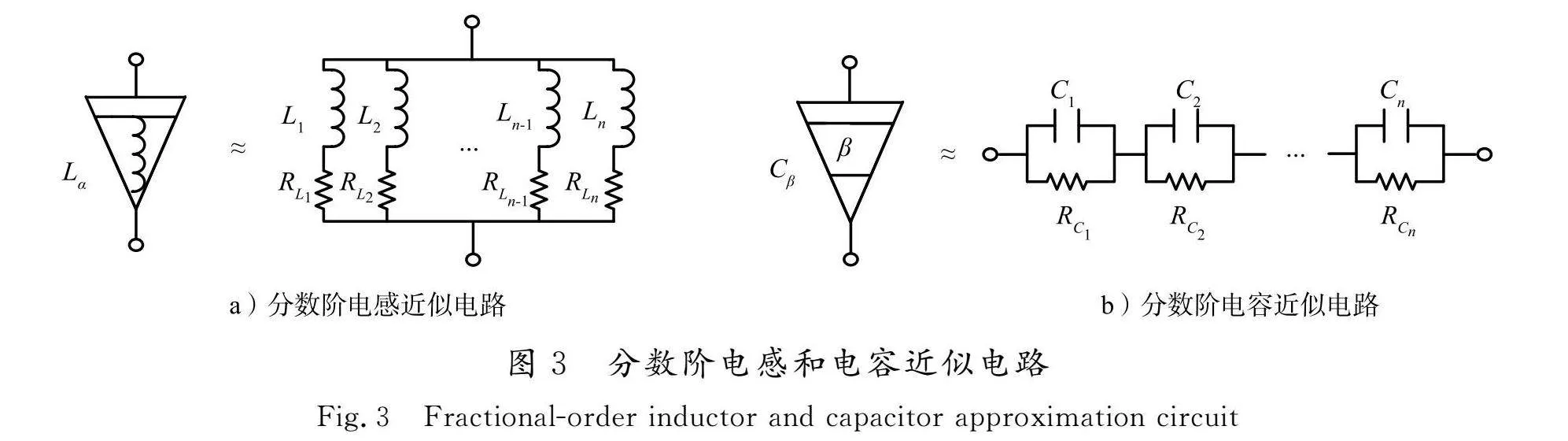
根据文献[9]和文献[10]，基于分抗链的分数阶微积分算法，分数阶电容和电感均采用RC、RL链式电路结构来实现，如图3所示。

此外，在分数阶微积分算法模块中， 存在如下参数： 滤波器阶数N、拟合频率下限ωb和拟合频率上限ωh[11-12]。需要根据实际分数阶系统的工作频率来选择拟合频率下限ωb和拟合频率上限ωh。在此，电路参数选择Uin=40 V，L=1 mH，C=1 mF，R=5 Ω，f=100 kHz，求得工作频率ω=2πf≈6.28×105 rad/s，需考虑高于开关频率的高频谐波， 从而ωh>6.28×105 rad/s。拟合频率段（ωb，ωh）一般选取ωbωh=1[13-14]。在此选择ωb=5×10-7 rad/s，ωh=2×106 rad/s。

反激变换器中常用的储能器件，在25 ℃（100 Hz～1 MHz）条件下其阶次主要集中在0.8和0.9阶。理论上阶数过低时，其感性成分和容性成分太小，使反激变换器无法正常工作，失去研究意义。因此本文主要选取实际中常见的2种阶次0.8和0.9进行讨论。当L=1 mH、α=0.8、N=5，或C=1 mF、β=0.8、N=7时，图3中的各个电阻值和各个电感电容值分别如表1所示。

当L=1 mH、α=0.9、N=5，或C=1 mF、β=0.9、N=7时，图3中的各个电阻值和各个电感电容值分别如表2所示。

3.2 分数阶反激变换器的状态平均模型与电路仿真模型的仿真对比

为了验证上述所建分数阶模型的正确性，依据3种工作模态下的状态方程，即式（4），在Matlab/Simulink中搭建电感电流断续模式下反激变换器的数值仿真模型如图4所示。

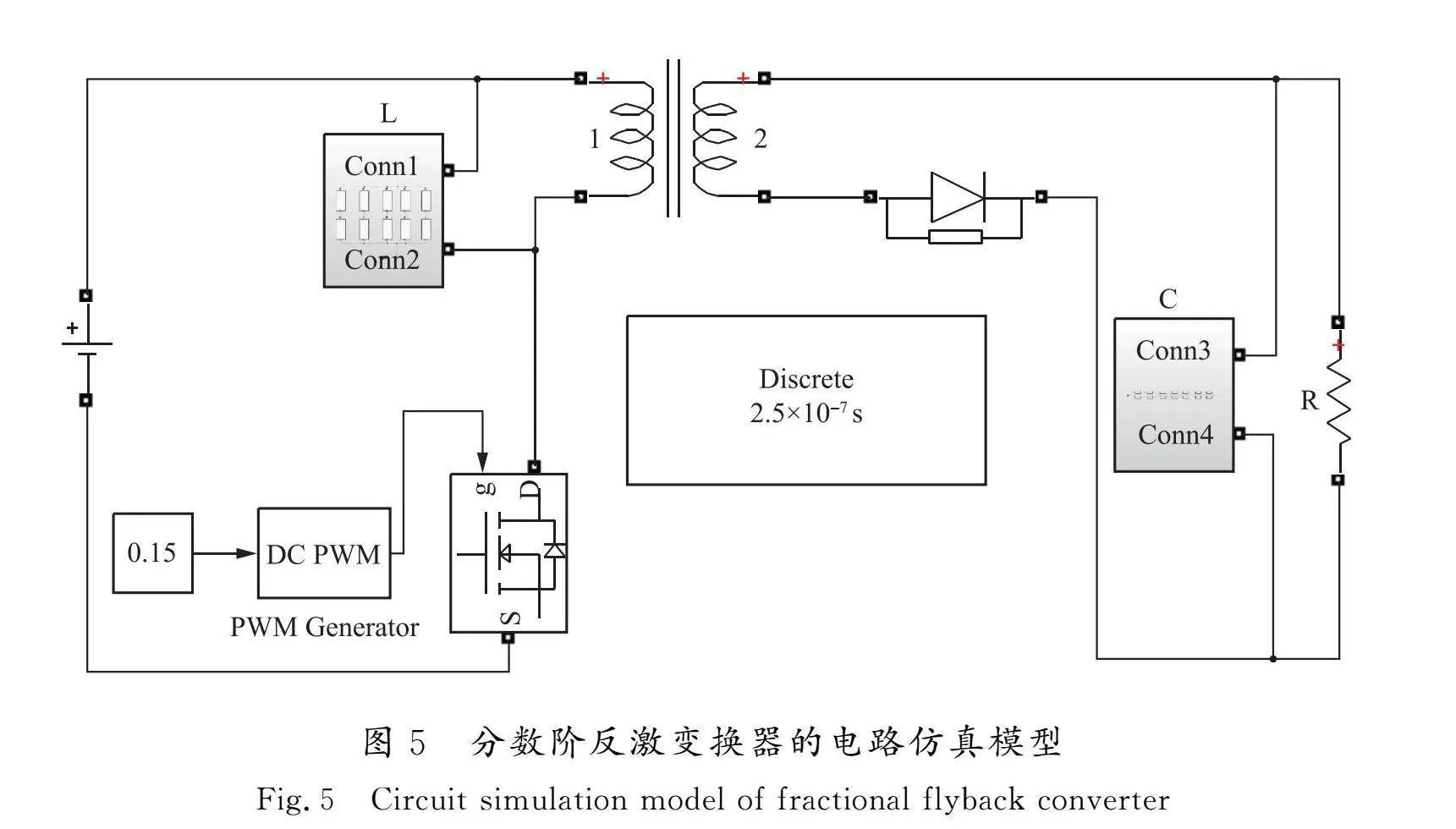
工作在电感电流断续模式下的分数阶反激变换器的电路仿真模型如图5所示。

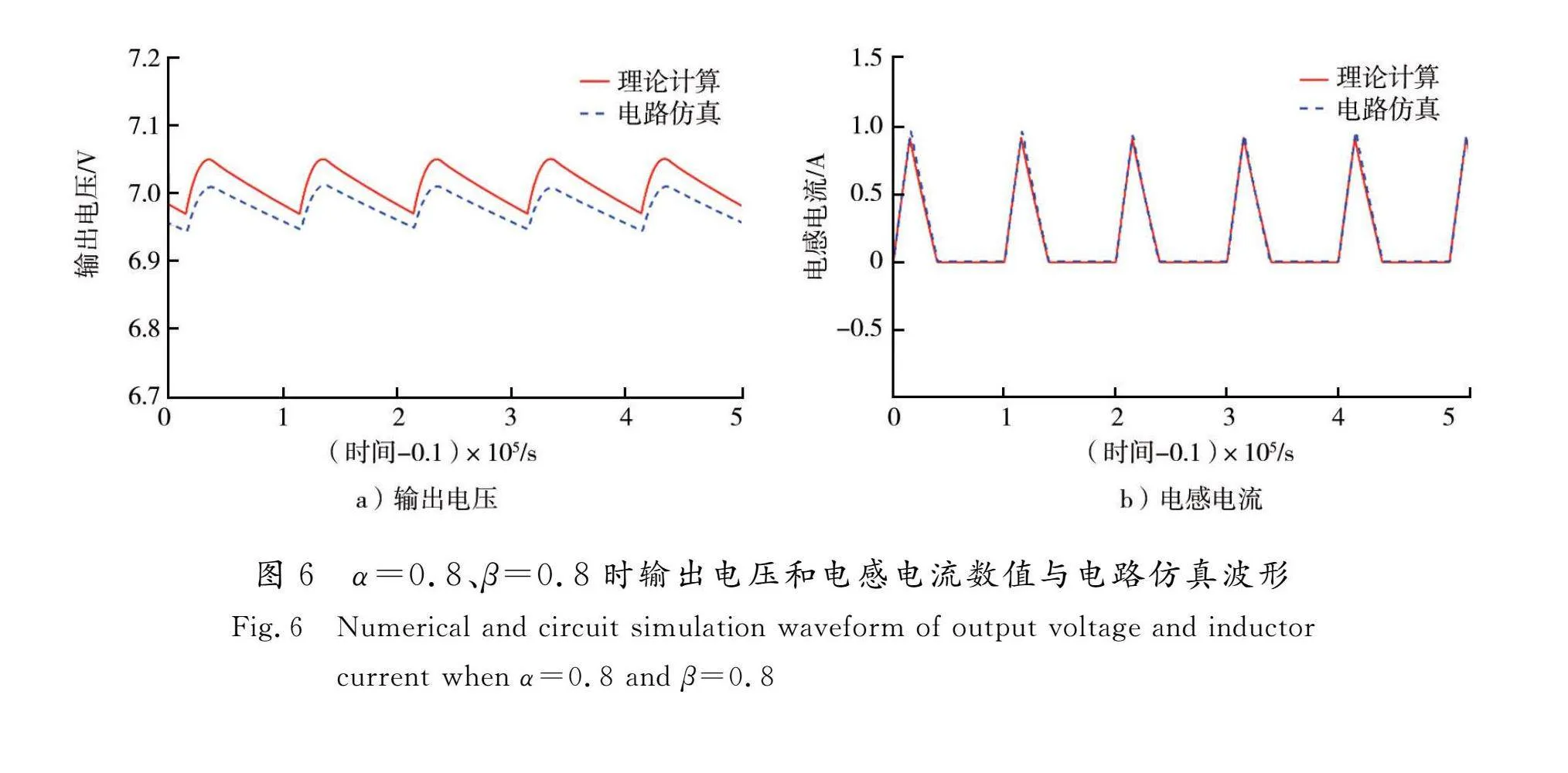
当α=0.8、β=0.8 ，在分数阶反激变换器运行到稳态时进行观察，输出电压uc和电感电流im波形如图6所示。

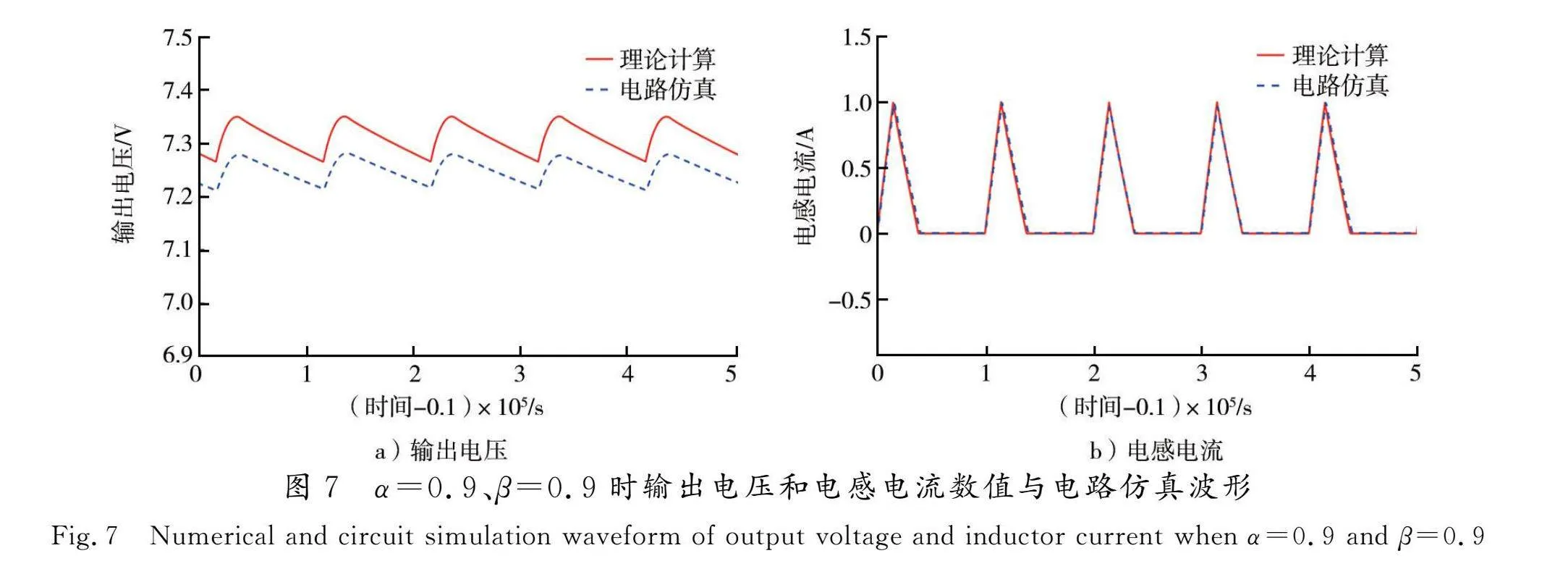
当α=0.9、β=0.9时，在分数阶反激变换器运行到稳态时进行观察，输出电压uc和电感电流im波形如图7所示。

从以上电感电流波形图中可以看出，变换器的电感电流为断续模式。对以上结果进行比较可以看出，电路仿真与理论分析基本一致，这验证了上述所建工作于电感电流断续模式下的反激变换器的分数阶建模的正确性，其中误差是由于分数阶电感、电容的近似电路所引起的。

4 实 验

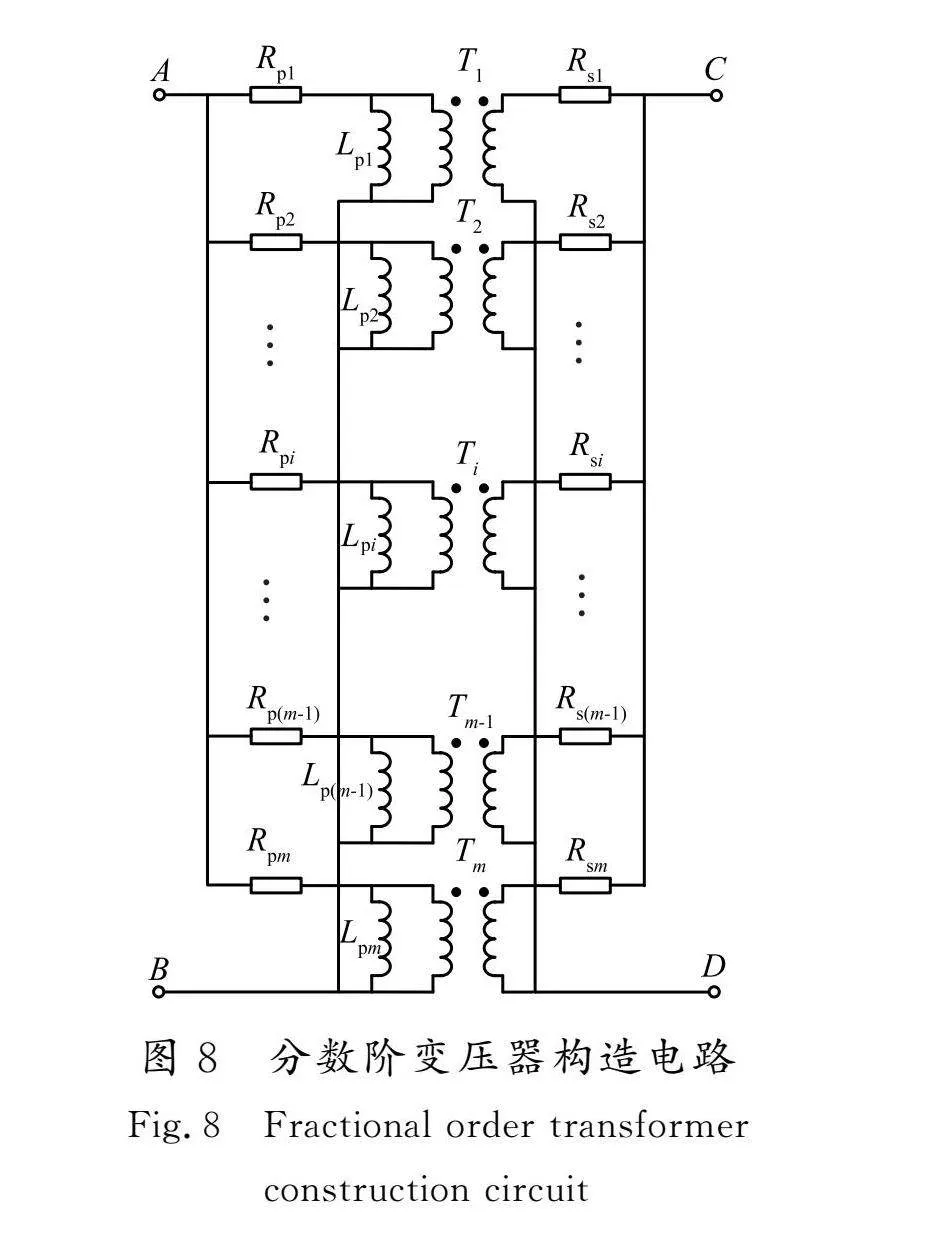
为了进一步验证理论分析的有效性，进行了实验测量。对于图1中带理想变压器的T模型的形式，在仿真软件中可以采用一个构造的分数阶电感与理想变压器并联的方式来模拟分数阶变压器。但是在实际中这种方式并不适用于实现分数阶变压器元件，因为实际电路中并不存在理想变压器。因此，需要采用其他方法来实现分数阶变压器。根据文献[15]得到分数阶变压器构造电路如图8所示。

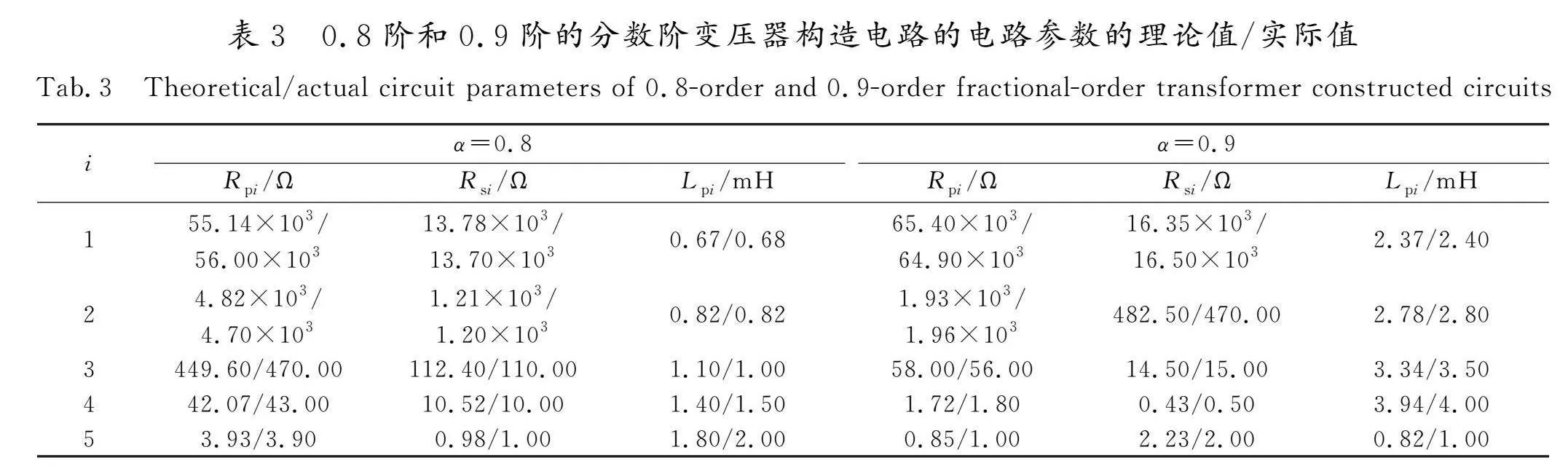
0.8阶和0.9阶原边伪电感值为1 mH/s1-0.8、副边伪电感值为0.25 mH/s1-0.8的分数阶变压器构造电路的电路参数的理论值/实际值如表3所示。

分数阶反激变换器实验电路如图9所示。其中包括分数阶电容、分数阶变压器以及为了保护开关管不被击穿加入的RCD钳位电路。

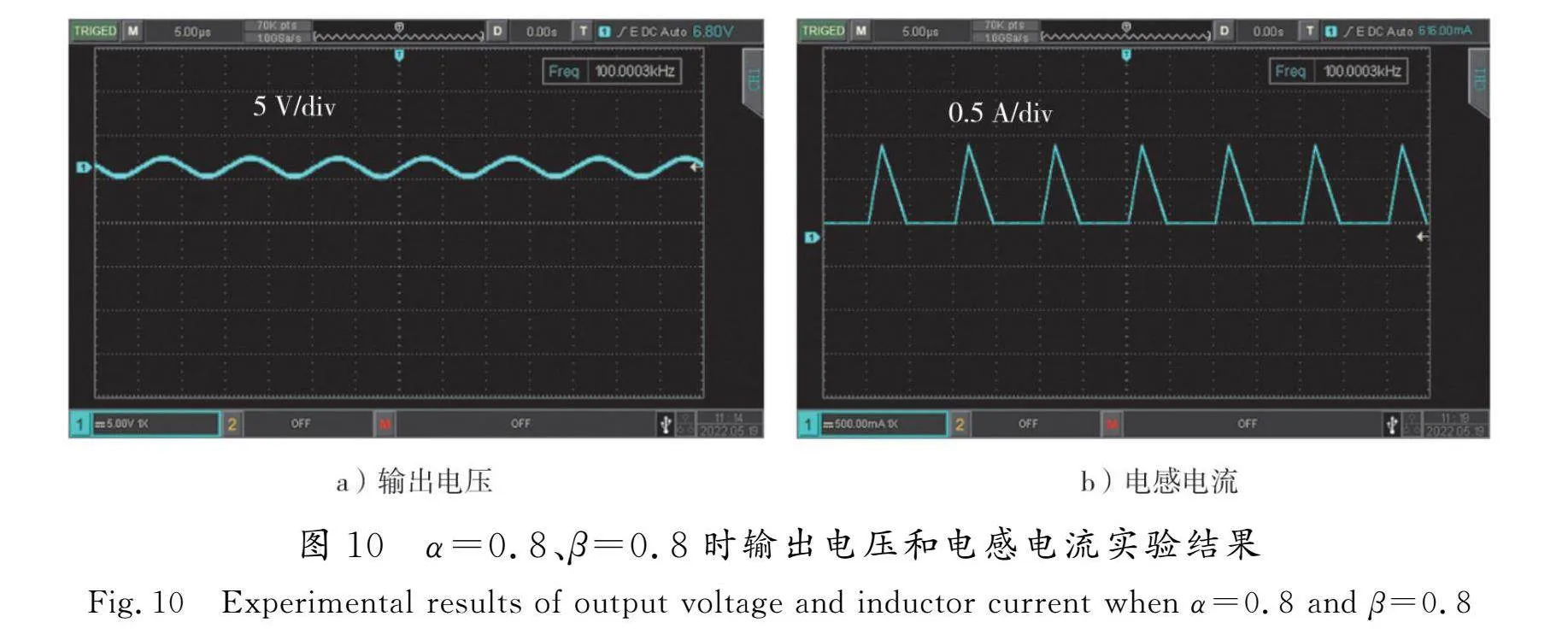
当α=0.8、β=0.8时，分数阶反激变换的输出电压uc和电感电流im波形的实验结果如图10所示。

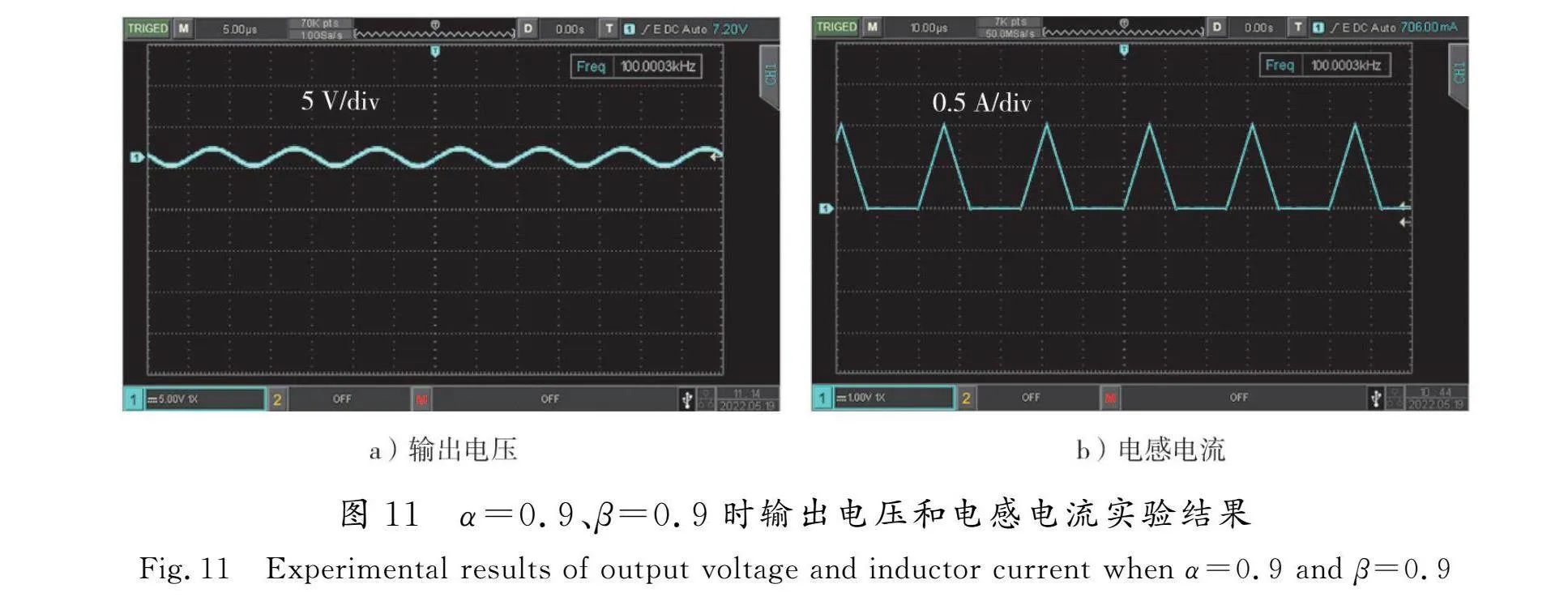
当α=0.9、β=0.9时，分数阶反激变换的输出电压uc和电感电流im波形的实验结果如图11所示。

实验结果、理论数值计算结果和Simulink实验仿真结果的对比如表4所示。

由表4可以看出，由于功率干扰和谐波效应的影响，实验结果的误差大于理论分析结果。2组电路仿真、理论分析和实验结果基本一致，这验证了所建立的分数阶模型的正确性。

5 结 语

基于分数阶微积分原理采用状态空间平均法，对工作在电感电流断续模式下的反激变换器进行建模与分析，通过仿真和实验验证了所建模型的正确性。仿真与实验结果表明，分数阶模型能够更为准确地描述反激变换器的真实特性，该精确建模对于反激变换器的性能分析及变换器闭环控制器的设计具有重要价值。

本文只开展了分数阶反激变换器开环系统的研究分析，未来拟进行分数阶反激变换器的闭环控制研究。

参考文献/References：

[1] 唐天缘.隔离型DC-DC变换器关键技术研究[D].成都：电子科技大学，2023.

TANG Tianyuan.Research on Key Technologies of Isolated DC-DC Converter[D].Chengdu：University of Electronic Science and Technology of China，2023.

[2] ZHU Binxin，YANG Yujin，WANG Kaihong，et al.High transformer utilization ratio and high voltage conversion gain flyback converter for photovoltaic application[J].IEEE Transactions on Industry Applications，2024，60（2）：2840-2851.

[3] 袁成功，张民，薛鹏飞，等.新型耦合电感高增益DC-DC变换器[J].太阳能学报，2023，44（4）：448-455.

YUAN Chenggong，ZHANG Min，XUE Pengfei，et al.Novel coupled inductor high-gain DC-DC converter[J].Acta Energiae Solaris Sinica，2023，44（4）：448-455.

[4] NWOKE J，VIOLA J，CHEN Yangquan.Fractional-order modeling and controls of a flyback converter for voltage regulation tasks[C]//2023 International Conference on Fractional Differentiation and Its Applications （ICFDA）.Ajman：IEEE，2023：1-5.

[5] YANG Chen，XIE Fan，CHEN Yanfeng，et al.Modeling and analysis of the fractional-order flyback converter in continuous conduction mode by caputo fractional calculus[J].Electronics，2020，9（9）：1544-1559.

[6] 刘翔，李晓峰，丁良贵，等.DCM反激变换器稳态分析与建模仿真[J].兵器装备工程学报，2020，41（3）：205-210.

LIU Xiang，LI Xiaofeng，DING Lianggui，et al.Steady-state analysis and research on modeling and simulation of DCM flyback converter[J].Journal of Ordnance Equipment Engineering，2020，41（3）：205-210.

[7] XIE Lingling，LIU Zhipei，ZHANG Bo.A modeling and analysis method for CCM fractional order buck-boost converter by using R-L fractional definition[J].Journal of Electrical Engineering & Technology，2020，15（4）：1651-1661.

[8] 杨可，苏尚流.基于状态空间平均法的反激变换器DCM小信号建模[J].通信电源技术，2021，38（2）：6-9.

YANG Ke，SU Shangliu.Small signal modeling of flyback converter in DCM with state-space averaging method[J].Telecom Power Technologies，2021，38（2）：6-9.

[9] XIE Fan，YANG Zhiqiang，YANG Chen，et al.Construction and experimental realization of the fractional-order transbdcefe54090529b47e7e1242f6bcf6fbformer by oustaloup rational approximation method[J].IEEE Transactions on Circuits and Systems II-Express Briefs，2023，70（4）：1550-1554.

[10]JIANG Yanwei，ZHANG Bo，SHU Xujian，et al.Fractional-order autonomous circuits with order larger than one[J].Journal of Advanced Research，2020，25：217-225.

[11]WIORA J，WIORA A.Influence of methods approximating fractional-order differentiation on the output signal illustrated by three variants of oustaloup filter[J].Symmetry，2020，12（11）：1898-1917.

[12]HAO Chunling，WANG Faqiang.Passive realization of the fractional-order capacitor based on fractional-order inductor and its application[J].International Journal of Circuit Theory and Applications，2023，51（6）：2607-2622.

[13]NAKO J，PSYCHALINOS C，ELWAKIL A S，et al.Design of higher-order fractional filters with fully controllable frequency characteristics[J].IEEE Access，2023，11：43205-43215.

[14]FANG Shucheng，WANG Xiaogang.Modeling and analysis method of fractional-order buck-boost converter[J].International Journal of Circuit Theory and Applications，2020，48（9）：1493-1510.

[15]杨晨.分数阶变压器构造及分数阶反激变换器建模分析[D].广州：华南理工大学，2021.

YANG Chen.Construction of Fractional Order Transformer and Modeling Analysis of fractional Order Flyback Converter[D].Guangzhou：South China University of Technology，2021.