发掘数学文化，融入“阅读与思考”栏目

摘 要：本文以三角函数与天文学为例，分析了数学文化融入“阅读与思考”栏目的意义，揭示数学文化对学习的激励作用，探讨了数学文化融汇设计方法，以具体的教学活动设计为例，展示了如何将理论知识与实践相结合，以实现提升学生学习兴趣和数学文化素养的目标.

关键词：三角函数；天文学；数学文化；教学活动

1 “阅读与思考”栏目设计

1.1 背景意义

在高中阶段设置“阅读与思考”栏目，是一种创新的教育尝试.以三角函数内容背景下的天文学材料为例，学生可以从中直观地看到数学在现实世界，尤其是在解决复杂天文问题中的应用.天文学作为一个探索宇宙，寻找人类在宇宙中位置的学科，充满了未知和神秘，能够很好地吸引学生的注意力.通过学习天文学中的数学应用，学生不仅能获得知识，还能被其中的探索精神所激励，激发对数学研究的兴趣.这样的学习过程打破了数学在学生心中抽象、难以理解的刻板印象，增强了他们学习数学的动力和信心.［1］此外，在解决天文学问题的过程中，需要学生综合运用所学的知识，将数学、物理等多个学科的知识交织在一起.这种跨学科的学习模式对于培养学生的综合分析能力、解决问题能力以及创新思维能力都有重要意义.

1.2 阅读材料案例

在天文学界，有一个谜题长久未解，即恒星距地球到底有多远.这个问题像是广袤宇宙对人类的挑战.直到19世纪初，德国天文学家威廉姆·贝塞尔（Wilhelm Bessel）向它发起了挑战.

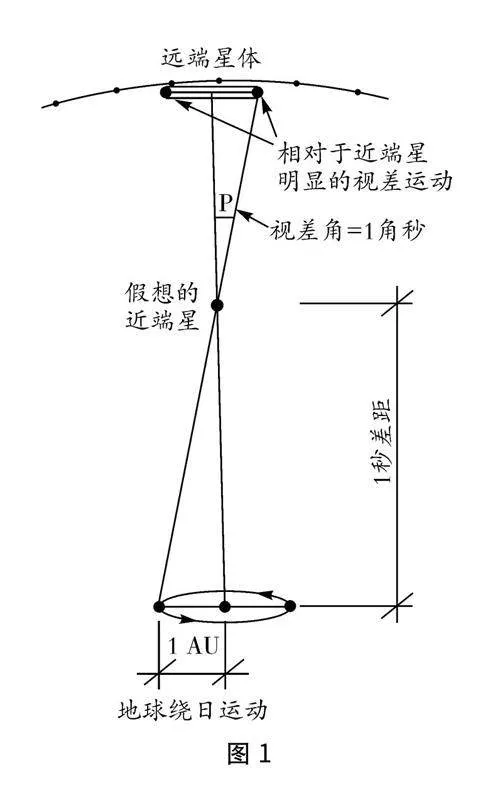
贝塞尔目光落在了一个名为天鹅座61的恒星上.这颗恒星因其相对地球的距离较近成为贝塞尔测量的理想目标.贝塞尔的策略是利用恒星视差（一种因观察者位置变化引起的视差效应）.地球在太阳周围的公转，使得位于不同位置的观察者看到近处的恒星相对于远处背景星空位置发生的微小变化.贝塞尔计划在一年中的两个不同时间（相隔六个月，确保地球在公转轨道的两侧）测量天鹅座61相对于更远恒星的位置，从而捕捉到这一微小变化.要捕捉这种几乎微不足道的变化，贝塞尔需要超越当时的技术极限，他使用了一种精密的测量仪器（赫歇尔式望远镜），并对其进行了改进，使其能够进行更为精确的角度测量.通过长时间的观测和记录，贝塞尔收集了大量数据，这些数据需要他进行复杂、精细的计算.

贝塞尔将这些观测数据带入三角学的框架中.通过测量恒星在六个月间的视差角即恒星相对于地球在太阳轨道两侧位置的视线角度变化，贝塞尔能够构建如图1所示的一个简单三角形，地球在其轨道上的两个观测点和恒星构成了这个三角形的顶点.利用基本的三角函数知识，他计算出了天鹅座61距离地球约10.4光年.

这一成就不仅是天文学史上的一座里程碑，也是人类首次触摸到恒星距离的壮举.贝塞尔的工作展示了三角学在解开宇宙奥秘中的强大力量，揭开了宇宙的一层神秘面纱，让人类第一次准确地量度了恒星的距离，也为后世的天文学家提供了测量恒星距离的方法.贝塞尔的成就，不仅是一次科学上的突破，更是人类对宇宙探索的证明.

2 面向栏目的数学文化融汇设计

2.1 讲述历史发展故事

三角学与天文学的结合，是人类理解宇宙的一个重要里程碑.首先，教师介绍三角学的起源和发展，古巴比伦人和古希腊人是最早记录和研究天体运动的文明，他们的工作为后来的三角学奠定了基础.通过对这一时期的探讨，学生可以了解到数学知识是如何在解决实际问题中诞生和发展的.其次，教师介绍阿拉伯学者在中世纪对三角学的贡献，他们不仅保留了古希腊的数学文献，还加以发展，将三角学推向了一个新的高度.最后，教师介绍欧洲文艺复兴时期，天文学家和数学家利用三角学原理来支持和验证他们的天文理论，展现数学与天文学交叉融合的魅力.通过这一系列历史发展的介绍，学生不仅能够了解到三角学的数学原理，还能够深刻理解这些数学工具是如何在人类文明进步中发挥作用的.

2.2 走进数学家的生平

每一个数学概念的背后，都有一位或多位数学家的身影，他们的生平故事，不仅是数学历史的一部分，更是激励后人的宝贵财富.在“三角函数与天文学”的教学中，教师引入数学家的生平故事，可以让学生更加生动地理解数学知识，感受数学家的智慧和创造力.以三角函数与天文学为例，教师可以带领学生深入了解那些对这一领域做出重大贡献的数学家和天文学家.例如，教师介绍希腊天文学家克罗狄斯·托勒密（Claudius Ptolemaeus）和他的《天文学大成》如何影响了后世对天体运动的理解；阿拉伯数学家阿尔·花剌子模（Al Xorazmiy）如何将希腊的三角学传入阿拉伯世界并加以发展.在数学家生平的学习中，学生不仅能学习到数学和天文学的知识，还能从中汲取追求真理和勇于探索的精神动力.这种人文关怀的融入，使得数学学习变得更加吸引人和有意义.

2.3 发掘经典数学思想

数学知识的学习，不只是学生对公式和定理的记忆，更重要的是学生要理解其中蕴含的思想和方法.在“三角函数与天文学”的教学中，教师通过发掘和讨论经典的数学思想，可以帮助学生深入理解数学概念，培养其抽象思维能力和创新能力.教师可以引导学生探讨和发掘三角函数在天文学中应用的经典思想，即如何通过观察和实验来验证理论，以及这些理论和实践如何推动了人类对宇宙的理解和探索.通过分析贝塞尔测量恒星距离的方法，学生可以深入了解三角视差的概念，以及它是如何帮助人类首次准确测量出恒星距离的.此外，教师可以设置思考题和讨论题，鼓励学生思考如果没有三角函数，人类会如何尝试测量天体距离，以及三角函数在现代天文学中的应用.通过发掘经典数学思想，学生可以理解数学不仅是工具，更是一种思维方式.这种思维方式的培养，对学生的学习和未来的生活都具有重要意义.

3 教学活动设计

3.1 历史场景复现

教学目标：构建基于历史事件的真实问题场景，激发学生的好奇心和探索欲，引入知识点.

问题1 在广袤的星系中存在着一颗恒星，你作为19世纪初一个知名的天文学家，通过大量的观测，知道了它的周年视差是0.04′′，那么它到地球的距离是多远？请自由分组，搜集关于“视差”“周年角位移”“天文单位”“角秒”和“秒差距”的概念，并利用三角视差法进行解答.

3.2 小组合作与探讨

教学目标：促进学生之间的交流与合作，通过解决实际问题来深化对三角函数知识的理解.

（1）概念搜集.视差是从两个不同位置观察一个物体时，物体相对于背景的位置看起来发生变化的现象；周年角位移是指由于地球绕太阳公转造成的，相对于远处恒星背景的，一个近邻恒星视位置的年度变化，这种变化形成了一个极小的角度，称为周年视差；天文单位AU（Astronomical Unit）是一个长度单位，定义为地球到太阳的平均距离，它用于测量和表达太阳系内天体的距离；角秒是测量天文学中角度的单位，1角秒为13 600度；秒差距是天文学中用来测量星际距离的单位，一秒差距定义为当一个天体的年视差为一角秒时，该天体与观测者之间的距离.

（2）问题解答.如图2所示，BC代表八月地球到恒星的距离，BOBC=sin α，BC=BOsin α.

由∠P=0.04″，则α=0.02″，则BC=1 AUsin 0.02″ =50秒差距，由于1秒差距=3.26光年，则BC=50×3.26=163（光年）.

3.3 综合提升与归纳

教学目标：通过测试和讨论，检验和巩固学生对三角函数知识的掌握，帮助学生总结知识点，提升解题能力.

问题2 函数f（x）=cos2x＋2sinxcosx，求出f（x）的最小正周期及单调递减区间；求出f（x）在区间0，π4上的最值.

思路过程：利用二倍角公式与两角和公式，将原式变化为f（x）=2sin2x＋π4，由周期性质得到最小正周期为π，继而得到单调递减区间为［π8＋kπ，5π8＋kπ］，k∈Z，故最大值为2，最小值为1.

归纳总结：教师总结本次教学活动的重点和难点，确保每位学生都能掌握关键知识点.

4 结语本文通过分析“三角函数与天文学”的实际案例，展现了数学文化融入“阅读与思考”栏目的重要作用.数学文化的融汇设计不仅丰富了学生的数学知识，还拓宽了他们的视野，激发了学生对科学探索的热情.［2］具体的教学活动设计能够进一步加深学生对数学概念的理解，培养他们的综合分析能力和创新思维.

参考文献

［1］屈小妹，闫晓亭，阳均.数学文化融入初中数学翻转课堂的研究与实践——以平方差公式为例［J］.湖北师范大学学报（自然科学版），2024（1）：104-109.

［2］肖忠伟.新课标下初中数学阅读思考型课堂的构建［J］.中学课程辅导，2023（25）：60-62.