突破原理题中的曲线归属和计算问题

《中国高考评价体系》中明确提出：关键能力是指即将进入高等学校的学习者在面对与学科相关的生活实践或学习探索问题情境时，高质量地认识问题、分析问题、解决问题所必须具备的能力。自2021年广东实行新高考以来，广东高考化学卷题型常规，保持稳定，情境陌生，创新性高，综合性和内容跨度大，知识串联性强，特别是有关原理题中的图像和计算问题，区分度明显，层次分明，很好的体现了关键能力的考查，有利于引导中学教学和高校选才。

近4年广东高考化学试题的计算分数越来越多，笔记进行粗略统计：2021年21分，2022年23分，2023年25分，2024年26分，而很多学生往往对计算题存在恐惧心理，能不做尽量不做，导致丢分严重，其实我们认真研究高考试题，发现广东近几年高考计算其实并不难，回归基础，回归概念教学，只要理解概念，运用概念的定义完全可以突破计算的难点。

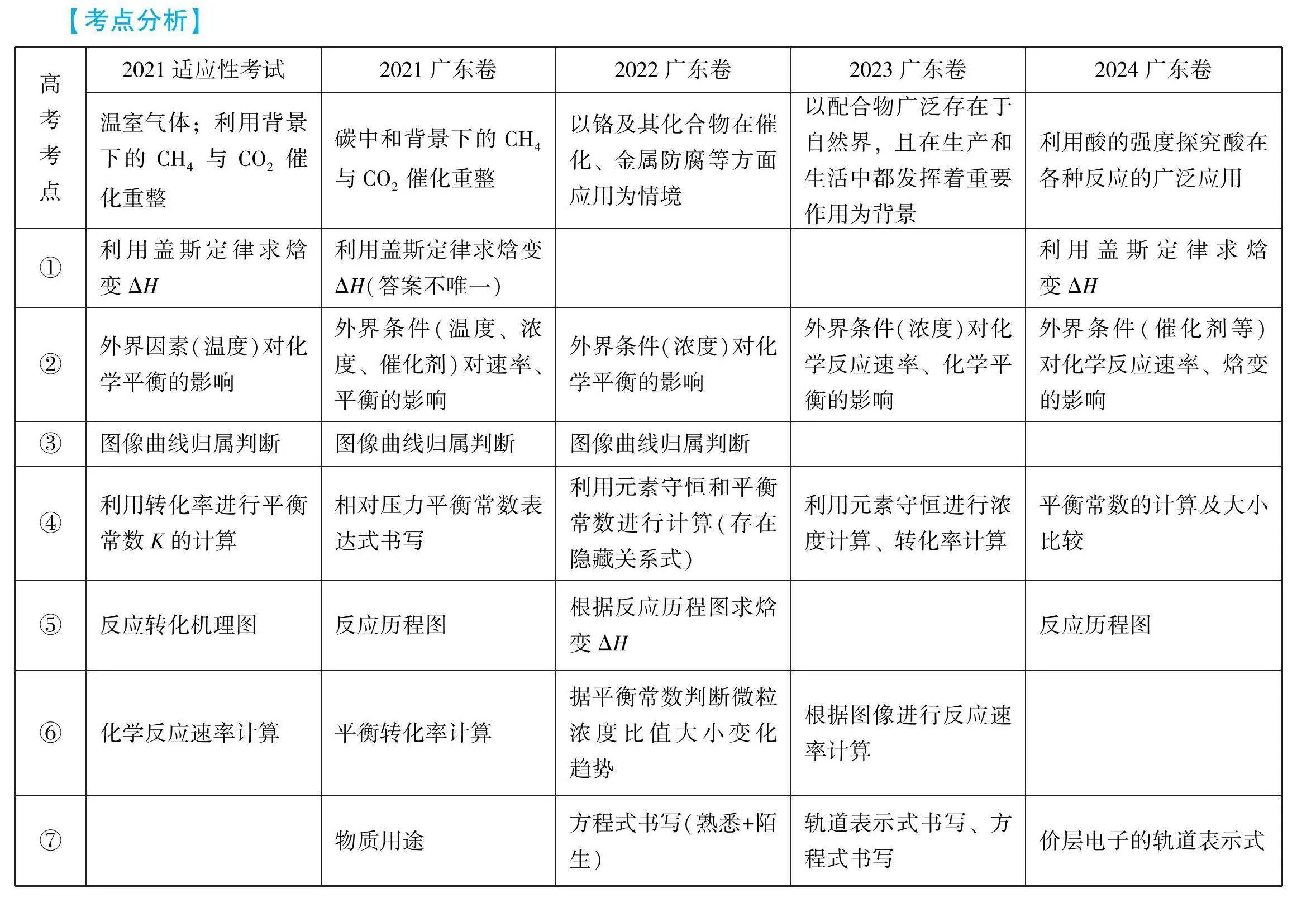
【考点分析】

一、曲线归属

【例1】（2023·新课标全国卷节选）向AgCl饱和溶液（有足量AgCl固体）中滴加氨水，发生反应Ag++NH3＼[Ag（NH3）＼]+和＼[Ag（NH3）＼]++NH3＼[Ag（NH3）2＼]+。lg＼[c（M）/（mol×L-1）＼]与lg＼[c（NH3）/（mol×L-1）＼]的关系如图1所示（其中M代表Ag+、Cl-、＼[Ag（NH3）＼]+或＼[Ag（NH3）2＼]+）。

【问题】如何判断图像中四条曲线的归属？

【解析】定性视角：根据平衡移动原理，分析各微粒浓度随氨水的不断滴入呈现出的变化趋势。根据题干信息分析，在AgCl饱和溶液中，存在平衡：AgCl（s）Ag+（aq）+Cl-（aq）。

Ag+和Cl-的浓度相等，向该饱和溶液中滴加氨水，由于氨水中的NH3·H2O与Ag+结合，导致溶液中Ag+浓度减小，Cl-浓度增大、＼[Ag（NH3）＼]+浓度增大，继续滴加氨水，＼[Ag（NH3）＼]+增大的幅度小于＼[Ag（NH3）2＼]+，则曲线I、Ⅱ、Ⅲ、Ⅳ分别表示＼[Ag（NH3）2＼]+、＼[Ag（NH3）＼]+、Ag+、Cl-的浓度随NH3浓度变化的曲线。

【例2】（2023·山东高考节选）在含HgI2（s）的溶液中，一定c（I-）范围内，存在平衡关系HgI2（s）HgI2（aq）；HgI2（aq）Hg2++2I-；HgI2（aq）HgI++I-；HgI2（aq）+I-HgI-3；HgI2（aq）+2I-HgI2-4，平衡常数依次为K0、K1、K2、K3、K4。已知lgc（Hg2+）、lgc（HgI+）、lgc（HgI-3）、lgc（HgI2-4）随lgc（I-）的变化关系如图2所示。

【问题】如何判断图像中四条曲线的归属？

【解析】定性视角：根据平衡移动原理，分析各微粒浓度随c（I-）增加呈现出的变化趋势。

分析方程式：HgI2（aq）Hg2++2I-；HgI2（aq）HgI++I-；随c（I-）增大，平衡逆向移动，c（Hg2＋）和c（HgI＋）降低；分析方程式：HgI2（aq）+I-HgI-3；HgI2（aq）+2I-HgI2-4，随c（I-）增大，平衡正向移动，c（HgI-3）和c（HgI2-4）增大，由此可以把曲线分成2组：1和2一组【c（Hg2+）和c（HgI+）】，3和L一组【c（HgI-3）和c（HgI2-4）】。再注意观察方程式，I-的计量数越大，则改变相同c（I-）的时候，影响程度越小，则线的斜率越大，由方程式可知，c（Hg2＋）和c（HgI2-4）受影响的程度相对较小，斜率大，则直线1、2、3、L分别代表lgc（Hg2+）、lgc（HgI+）、lgc（HgI-3）、lgc（HgI2-4）随lgc（I-）变化的图像。

【例3】（2023·辽宁高考节选）某废水处理过程中始终保持H2S饱和，即c（H2S）=0.1mol·L-1，通过调节pH使Ni2+和Cd2+形成硫化物而分离，体系中pH与-lgc关系如图3所示，c为HS-、S2-、Ni2+和Cd2+的浓度，单位为mol·L-1。已知Ksp（NiS）>Ksp（CdS）。

【问题】如何判断图像中四条曲线的归属？

【解析】定性视角：根据平衡移动原理，分析各微粒浓度随pH增加呈现出的变化趋势。

注意纵坐标为-lgc，纵坐标越大，c越小。分析方程式：H2S（aq）H++HS-、HS-H++S2，随着pH的增大，H2S的浓度逐渐减小，HS-的浓度增大，S2-浓度逐渐增大，则有-lgc（HS-）和-lgc（S2-）随着pH增大而减小，S2-浓度逐渐增大会导致Ni2+和Cd2+浓度逐渐减小，则可以分为两组：③和④代表-lgc（HS-）和-lgc（S2-），①和②代表-lgc（Ni2+）、-lgc（Cd2+）；有根据“始终保持H2S饱和”，则pH相同时，HS-浓度大于S2-，即-lgc（HS-）小于-lgc（S2-），则③代表-lgc（S2-）-，④代表-lgc（HS-）【或者直接看起点也可以】。Ksp（NiS）>Ksp（CdS），即当c（S2-）相同时，c（Ni2+）＞c（Cd2+），则-lgc（Ni2+）小于-lgc（Cd2+），由此可知曲线①代表-lgc（Cd2+）、②代表-lgc（Ni2+）。

【例4】（2024·全国甲卷节选）将0.10 mmol Ag2CrO4配制成1.0 mL悬浊液，向其中滴加0.10 mol·L-1的NaCl溶液。lg［cM/（mol·L-1）］（M代表Ag+、Cl-或CrO2-4）随加入NaCl溶液体积（V）的变化关系如图所示。

【问题】如何判断图像中3条曲线的归属？

【解析】定量视角：根据平衡移动原理和特殊的点，寻找刚好完全反应的点突破曲线的归属问题。向1.0 mL含0.10 mmolAg2CrO4的悬浊液中滴加0.10 mol·L-1的NaCl溶液，发生反应：Ag2CrO4（s）+2Cl-（aq）2AgCl（s）+CrO2-4（aq），两者恰好完全反应时，NaCl溶液的体积为V（NaCl）=2×0.10 mmol0.10 mol/L=2 mL，2 mL之后再加NaCl溶液，c（Cl-）增大，据AgCl（s）Ag+（aq）+Cl-（aq），Ksp（AgCl）=c（Ag+）·c（Cl-）可知，c（Ag+）会随着c（Cl-）增大而减小，所以2mL后降低的曲线，即最下方的虚线代表Ag+，升高的曲线，即中间虚线代表Cl-，则剩余最上方的实线为CrO2-4曲线。

【解题策略】

注意审题，分清楚图像横坐标、纵坐标的含义，厘清图像是否为平衡状态的图像，注意获取题干中文字信息、方程式信息、巧妙利用图像特殊点（起点、交点、突变点、数值整数点等），深度理解勒夏特列原理，关注曲线变化趋势，以此来破解图像的归属问题。

二、经典计算

【例1】（2024·全国甲卷节选）甲烷转化为多碳化合物具有重要意义。一种将甲烷溴化再偶联为丙烯（C3H6）的研究所获得的部分数据如下。回答下列问题。

（1）已知如下热化学方程式：

CH4（g）+Br2（g）=CH3Br（g）+HBr（g）

ΔH1=-29 kJ·mol-1

3CH3Br（g）=C3H6（g）+3HBr（g）

ΔH2=+20 kJ·mol-1

（2）CH4与Br2反应生成CH3Br，部分CH3Br会进一步溴化。将8 mmol CH4和8 mmol Br2，通入密闭容器，平衡时，n（CH4）、n（CH3Br）与温度的关系见图5所示（假设反应后的含碳物质只有CH4、CH3Br和CH2Br2）。

（ⅰ）图中CH3Br的曲线是 （填“a”或“b”）。

（ⅱ）560℃时，CH4的转化α= ，

n（HBr）= mmol。

（ⅲ）560℃时，反应CH3Br（g）+Br2（g）=CH2Br2（g）+HBr（g）的平衡常数K= 。

【解析】本小题考查化学平衡的移动及曲线的归属，转化率和平衡常数的计算等问题，解答此类题的核心关键是列出表达式，一一求出对应的量，代入公式进行相关计算。

（ⅰ）根据方程式①，升高温度，反应向吸热反应方向移动，即平衡逆向移动，CH4（g）的含量增多，CH3Br（g）的含量减少，故CH3Br的曲线为a。

（ⅱ）观察图像可知，560℃时反应达平衡，剩余的CH4（g）的物质的量为1.6 mmol，其转化率α=转化的CH4起始的CH4=（8 mmol-1.6 mmol）8 mmol×100%=80%；若只发生一步反应，则生成6.4 mmol CH3Br，但此时剩余CH3Br的物质的量为5.0 mmol，说明还有1.4 mmol CH3Br发生反应生成CH2Br2，则此时生成的HBr的物质的量n=6.4+1.4=7.8 mmol。

（ⅲ）平衡时，反应中各组分的物质的量分别为n（CH3Br）=5.0 mmol、n（Br2）=0.2 mmol、n（CH2Br2）=1.4 mmol、n（HBr）=7.8 mmol，故该反应的平衡常数K=c（CH2Br2）·c（HBr）c（CH3Br）·c（Br2）=1.4V×7.8V5.0V×0.2V=10.92。

【答案】（ⅰ）a （ⅱ）80%，7.8 （ⅲ）10.92

【例2】（2024·广东卷节选）在非水溶剂中研究弱酸的电离平衡有重要科学研究价值。一定温度下，某研究组通过分光光度法测定了两种一元弱酸HX（X为A或B）在非水溶液中的Ka。

a.选择合适的指示剂HIn，Ka（HXn）=3.6×10-20;其钾盐为KIn。

b.向KIn溶液中加入HX，发生反应：In-+HXX-+HIn。KIn的起始的物质的量为n0（KIn），加入HX的物质的量为n（HX），平衡时，测得c平（In-）/c平（HIn）随n（HX）/n0（KIn）的变化曲线如图所示。

已知：该溶剂不电离，钾盐在该溶剂中完全电离。

①计算Ka（HA）。（写出计算过程，结果保留两位有效数字）

②在该溶剂中，Ka（HB） Ka（HA）;Ka（HB） Ka（HIn）。（填“>”、“<”或“=”）

【解析】本小题考查多重平衡中化学平衡常数的计算等问题，解答此类题的核心关键是列出表达式，找到特殊点为突破口，融合、进行关系的转换，再代入公式进行相关计算。

①确定HA曲线，选择特殊的点（1，3），此时，c平（In-）/c平（HIn）=3，n（HX）/n0（KIn）=1，根据KIn的起始的物质的量为n0（KIn），则起始的n（HX）=n0，再根据In元素守恒，平衡时候：n平（In-）=34n0，n平（HIn）=14n0。

根据Ka（HIn）=c（H+）·c（In-）c（HIn）=3.6×10-20，推出c（H+）=1.2×10-20mol·L-1

根据三段式：In-+ HX X-+ HIn

起始：n0 n0 0 0

变化：14n014n014n014n0

平衡：34n034n014n014n0

再根据Ka（HA）=c（H+）·c（A-）c（HA）=

c（H+）·n（A-）n（HA）=1.2×10-20×14n034n0=4.0×10-21。

②确定曲线HB，选择特殊的点（1，0.4），根据同样的方法，可以快速求出Kb（HA）=2.25×10-19。

【答案】①4.0×10-21②>，>

【例3】（2023·广东卷节选）（3）R的衍生物L可用于分离稀土。溶液中某稀土离子（用M表示）与L存在平衡：

M+LML K1

ML+LML2 K2

研究组配制了L起始浓度c0（L）=0.02 mol·L-1、M与L起始浓度比c0（M）/c0（L）不同的系列溶液，反应平衡后测定其核磁共振氢谱。配体L上的某个特征H在三个物种L、ML、ML2中的化学位移不同，该特征H对应吸收峰的相对峰面积S（体系中所有特征H的总峰面积计为1）如下表。

【注】核磁共振氢谱中相对峰面积S之比等于吸收峰对应H的原子数目之比；“<0.01”表示未检测到。

①c0（M）/c0（L）=a时，x= 。

②c0（M）/c0（L）=b时，平衡浓度比c平（ML2）∶c平（ML）= 。

（4）研究组用吸收光谱法研究了（3）中M与L反应体系。当c0（L）=1.0×10-5 mol·L-1时，测得平衡时各物种c平/c0（L）随c0（M）/c0（L）的变化曲线如图7所示。

c0（M）/c0（L）=0.51时，计算M的平衡转化率（写出计算过程，结果保留两位有效数字）。

【解析】本题以各种配合物为载体，通过对化学反应速率、转化率等知识进行设问，考查学生综合运用化学反应原理解释问题、解决实际问题的能力，吸收运用新知识的能力。

（3）①由信息“体系中所有特征H的总锋面积为1”可知c0（M）/c0（L）=a时，x+0.64=1，则x=0.36。

②c0（M）/c0（L）=b时，平衡浓度比c平（ML2）∶c平（ML）=12S（ML2）∶S（ML）=12×0.6∶0.4=3∶4。

（4）根据公式：α（M）=M（转化）M（起始）=c转（M）c0（M）

找到图像中特殊点：c0（M）/c0（L）=0.51时，则c0（M）=0.51c0（L）

根据纵坐标，c平（ML）=c平（L）=0.4c0（L）

由L守恒可得：c0（L）=c平（L）+c平（ML）+

2c平（ML2），则c平（ML2）=0.1c0（L）

c转（M）=c平（ML）+c平（ML2）=0.5c0（L）

α（M）=0.5c0（L）/0.51c0（L）≈98%。

【答案】（3）①0.36 ②3∶4（4）98%

【例4】（2024·顺德三模节选）Fe3+会与溶液中的Cl-形成多种配合物。当c（Cl-）＜0.1 mol·L-1时，溶液中主要存在下列两个平衡：

Fe3++Cl-FeCl2+

K1=101.8

FeCl2++Cl-FeCl+2

K2=100.6

改变Cl-起始浓度，测得平衡时Fe3+、FeCl2+和FeCl+2的物质的量分数δ（x）随lgc（Cl-）的部分变化如图8所示。

已知：δ（x）=c（x）c（Fe3+）+c（FeCl2+）+c（FeCl-2），若Q点Fe3+对应的起始浓度c0（Fe3+）=a mol·L-1

（Ⅰ）求Q点溶液中c（Cl-）= mol·L-1；

（Ⅱ）计算Q点溶液中Fe3+的平衡转化率。（写出计算过程，已知100.6≈4）

【解析】本题以铁的配合物为载体，通过对离子浓度、转化率的计算，考查学生读图能力、利用元素守恒法进行计算的技巧。

方法一：设Q点溶液中

c（Fe3+）=c（FeCl+2）=x mol·L-1：

根据K1=c（FeCl2+）c（Fe3+）c（Cl-）=101.8，推出：

c（FeCl2+）=100.6x

则α（Fe3+）=c（FeCl2+）+c（FeCl+2）c（Fe3+）+c（FeCl2+）+c（FeCl+2）=

100.6x+xx+100.6x+x=56

方法二：设Q点溶液中c（Fe3+）=c（FeCl+2）=x mol·L-1，c（FeCl2+）=y mol·L-1

已知c（Fe3+）+c（FeCl+2）+c（FeCl2+）=amol·L-1

K1=c（FeCl2+）c（Fe3+）c（Cl-），即y10-12x=101.8

2x+y=a y=100.6x=4x

得：x=a6 y=2a3

M点溶液中Fe3+的转化率为83.3%（或56）。

【根据第2个方程式计算同样可以，合理方法都行】

【解题策略】

回归基础，理解转化率、反应速率、各种平衡常数的定义并且能够活用，例如：α=变化量起始量，

v=变化的量时间，这个“量”可以是物质的量、浓度、质量、压强等；K=生成物（x）的幂之积反应物（x）的幂之积，

如果“x”代表浓度，则K为一般的浓度平衡常数；如果“x”代表分压，则K为压力平衡常数（Kp）；如果“x”代表相对分压，则K为相对压力平衡常数（Krp）。无论是何种计算，都离不开利用方程式进行三段式计算或根据元素守恒，结合题目中的特殊点进行突破。

三、综合应用

【练习1】（2021·广东卷节选）我国力争于2030年前做到碳达峰，2060年前实现碳中和。CH4与CO2重整是CO2利用的研究热点之一。该重整反应体系主要涉及以下反应：

a）CH4（g）+CO2（g）2CO（g）+2H2（g） ΔH1

b）CO2（g）+H2（g）CO（g）+H2O（g） ΔH2

c）CH4（g）C（s）+2H2（g） ΔH3

d）2CO（g）CO2（g）+C（s） ΔH4

e）CO（g）+H2（g）H2O（g）+C（s） ΔH5

（4）设Krp为相对压力平衡常数，其表达式写法：在浓度平衡常数表达式中，用相对分压代替浓度。气体的相对分压等于其分压（单位为kPa）除以p0（p0=100 kPa）。

反应a、c、e的lnKrp随1T（温度的倒数）的变化如图9所示。

①反应a、c、e中，属于吸热反应的有 （填字母）。

②反应c的相对压力平衡常数表达式为lnKrp= 。

③在图9中A点对应温度下、原料组成为n（CO2）∶n（CH4）=1∶1、初始总压为100 kPa的恒容密闭容器中进行反应，体系达到平衡时H2的分压为40 kPa。计算CH4的平衡转化率，写出计算过程。

【解析】图9所示为Krp～1T之间的线性关系，根据化学平衡常数K与化学反应热效应之间的关系可知：对于吸热反应，随着温度升高，平衡常数K值增大；对于放热反应，随着温度升高，平衡常数K值减小。图9中所示横坐标为1T（温度的倒数），则lnKrp随着1T的增大而减小的曲线对应的反应为吸热反应，故答案为ac。

根据题干中的信息可知，相对分压平衡常数为生成物气体的相对分压幂之积比上反应物气体相对分压幂之积，由于C为固态，不写入平衡常数表达式。

由图可知，A点对应反应c的lnKpr=0，则

Kpr=（p（H2）p0）2p（CH4）p0=1

即p平（CH4）=p2（H2）p0

已知反应平衡时p平（H2）=40 kPa，则

p平（CH4）=p2（H2）p0=（40 kPa）2100 kPa=16 kPa

且已知初始状态时

p始（CH4）=12×100 Pa=50 KPa

故CH4的平衡转化率

α（CH4）=p始（CH4）-p平（CH4）p始（CH4）×100%=

50 kPa-16 kPa50 kPa×100%=68%

【答案】（4）①ac ②（p（H2）p0）2p（CH4）p0 ③68%

【练习2】（2020·全国甲卷节选）二氧化碳催化加氢合成乙烯是综合利用CO2的热点研究领域。回答下列问题。

（1）CO2催化加氢生成乙烯和水的反应中，产物的物质的量之比n（C2H4）∶n（H2O）= 。

（2）理论计算表明，原料初始组成n（CO2）∶n（H2）=1∶3，在体系压强为0.1 MPa，反应达到平衡时，四种组分的物质的量分数x随温度T的变化如图所示。

图中，表示C2H4、CO2变化的曲线分别是 、 。

（3）根据图中点A（440K，0.39），计算该温度时反应的平衡常数Kp= （MPa）-3（列出计算式。以分压表示，分压=总压×物质的量分数）。

【解析】（1）根据题意，CO2催化加氢生成乙烯和水的化学方程式可表示为2CO2+6H2→CH2=CH2+4H2O，可得n（C2H4）∶n（H2O）=1∶4。

（2）一定要认真注意审题：“反应达到平衡时，四种组分的物质的量分数x随温度T的变化如图所示”，本题考查的是平衡后温度的影响，很多同学容易出错：b、d一直减小为反应物，a、c增加为生成物。由题中信息可知，两反应物的初始投料之比等于化学计量数之比，由于消耗的n（CO2）和n（H2）也为1∶3，因此平衡时n（CO2）；n（H2）始终等于1∶3，产物中n（C2H4）∶n（H2O）始终等于1∶4，找出图中曲线的起点或特殊点坐标，可知a为H2，c为CO2，b为H2O，d为C2H4。

（3）理解分压和Kp的含义，代入公式。总压p=0.1 MPa，且根据反应物之间的物质的量的关系，n（CO2）∶n（H2）=1∶3，n（C2H4）∶n（H2O）=1∶4

2CO2（g）+6H2（g） C2H4（g）+4H2O（g）

平衡分压

0.393p0.39p0.394p0.39p

平衡常数Kp=0.394×0.3940.396×0.3932×10.13（MPa）-3=94×10.0393（MPa）-3。

【答案】（1）1∶4 （2）d c （3）94×10.0393或0.394×0.3940.396×（0.393）2×10.13

纵观近几年化学平衡题，占分比重一直在增加，但是学生得分率一直不高，究其原因，并不是题目太难，只是很多学生对图像和计算存在畏惧心理，实际只要同学们静下心来认真分析，寻找突破口，列出公式，寻找公式中的数值，步步为营，一定会解决这类问题。另外，在平时的复习中，多研究历年高考真题，高考试题永远是经典，特别是广东高考化学试题，真正把课本知识与“具体真实的世界”联系起来，通过优化考查内容、丰富呈现方式、创新设问角度等途径，突出对关键能力的考查，查学生灵活运用所学知识方法分析和解决实际问题的能力，引导学生在解决实际问题的过程中建构知识、培养能力、提升素养，让善于独立思考、认知能力强的学生脱颖而出。特别是广东高考原理题，强调思维过程和思维方式，鼓励学生多角度主动思考、深入探究，发现新问题、找到新规律，引导学生在学习和备考中减少死记硬背和机械刷题，真正做到了有效引导教学，实现高考由“以纲定考”到“考教衔接”的转变。

【作者简介：中学化学高级教师，顺德区教育发展中心高中化学教研员。曾获荣誉：顺德区骨干教师、顺德区教书育人优秀教师、佛山市首届高中化学优秀青年教师、佛山市优秀班主任等】

责任编辑 李平安