把正态分布的根留住

2024年是高考数学题型（8+3+3+5）改革的第一年，除了较难的个别大题的末小问考查数学创新能力与数学素养之外，其它题目都能找到课本中的原型与出处，体现了“回归课本应知应会，考查素养挑选人才”这两层命题意图．下面以试题中第9题有关正态分布的知识考查为例，阐述试题特点，思考2025年高考复习方略，以提高学子高考数学成绩.

一、高考试题

【2024年高考数学新课标第9题（多选题）】试题如下：

为了解推动出口后的亩收入（单位：万元）情况，从该种植区抽取样本，得到推动出口后亩收入的样本均值x-=2.1，样本方差s2=0.01，已知该种植区以往的亩收入X服从正态分布N1.8，0.12，假设推动出口后的亩收入Y服从正态分布N（x-，s2），则（ ）

（若随机变量Z服从正态分布Nu，σ2，P（Z<u+σ）≈0.8413）

A． P（X>2）>0.2 B． P（X>2）<0.5

C． P（Y>2）>0.5 D． P（Y>2）<0.8

【答案】BC

【解析】如图1-1，根据正态分布的3σ原则，

依题可知，x-=2.1，s2=0.01，

所以Y～N2.1，0.12，

由曲线的对称性可得：

PY>2=PY>2.1－0.1=

PY<2.1+0.1≈0.8413>0.5，

C正确，D错误；

因为X～N1.8，0.12，所以PX>2=PX>1.8+2×0.1，

因为PX<1.8+0.1≈0.8413，所以由曲线可得PX>1.8+0.1≈1－0.8413=0.1587<0.2，

而由曲线可得PX>2=PX>1.8+2×0.1<PX>1.8+0.1<0.2，

B正确，A错误，

故选：BC．

二、试题出处

试题出处在课本选择性必修三课本P87练习第2题，习题7.5复习巩固第2题．

1． 选择性必修三课本P87练习第2题

设随机变量X～N0，22，随机变量Y～N0，32，画出分布密度曲线草图，并指出PX≤－2与PX≤2的关系，以及PX≤1与PY≤1之间的大小关系．

答案：分布密度曲线草图如图2-1．

由曲线的对称性得PX≤－2=1－PX≤2，PX≤1>PY≤1.

2． 习题7.5复习巩固第2题

某市高二年级男生的身高X（单位：cm）近似服从正态分布N170，52，随机选择一名本地高二年级的男生，求下列事件的概率：

（1）165<X≤175； （2）X≤165； （3）X>175．

答案：

（1）P165<X≤175≈0.6827．

（2）PX≤165=PX≤170－P165<X≤170

≈121－0.6827≈0.1587．

（3）PX>175=121－P165<X≤175

≈121－0.6827≈0.1587．

三、把根留住

1．正态分布的概念

（1）若随机变量X的概率密度函数为f（x）=1σ2πe－（x－μ）22σ2，x∈R，其中μ∈R，δ>0为参数，则称随机变量X服从正态分布，记为X～Nμ，δ2．如图3-1为钟形正态曲线，关于直线x=μ对称．

特别地，当μ=0，δ=1时，称随机变量X服从标准正态分布，如图3-2．

（2）若X～Nμ，δ2，则X取不超过x的概率PX≤x为图中阴影部分的区域A的面积，而Pa≤X≤b为区域B的面积．如图3-3．

2．正态分布的期望与方差

若X～Nμ，δ2，则E（x）=μ D（x）=δ2.

3．正态曲线的性质

①曲线在x轴的上方，与x轴不相交；

②曲线关于直线x=μ对称；

③曲线在x=μx=μ时达到峰值1σ2π；

④曲线与x轴之间的面积为1；

⑤当x<μ时，曲线从左向右上升；当x>μ时，曲线从左向右下降．并且当曲线向左、右两边无限延伸时，以x轴为渐进线，向它无限靠近；

⑥曲线的形状由σ确定，σ越大，峰值1σ2π越小，曲线越“矮胖”，表示总体的分布越分散；σ越小，峰值1σ2π越大，曲线越“瘦高”，表示总体的分布越集中．

4．3σ原则

假设X～N（μ，σ2），对于给到的k∈N*，Pμ－kδ<x≤μ+kδ是一个只与k有关的定值，特别地，

Pμ－δ<x≤μ+δ=0.6827；

Pμ－2δ<x≤μ+2δ=0.9545；

Pμ－3δ<x≤μ+3δ=0.9973．

在实际应用中，尽管正态变量的取值范围是－SymboleB@，+SymboleB@，但在一次试验中，通常认为服从于正态分布Nμ，δ2的随机变量几乎总是落在区间μ－3δ，μ+3δ内，而在此区间以外的取值概率大约只有0.0027，我们把这一规律简称为3δ原则．

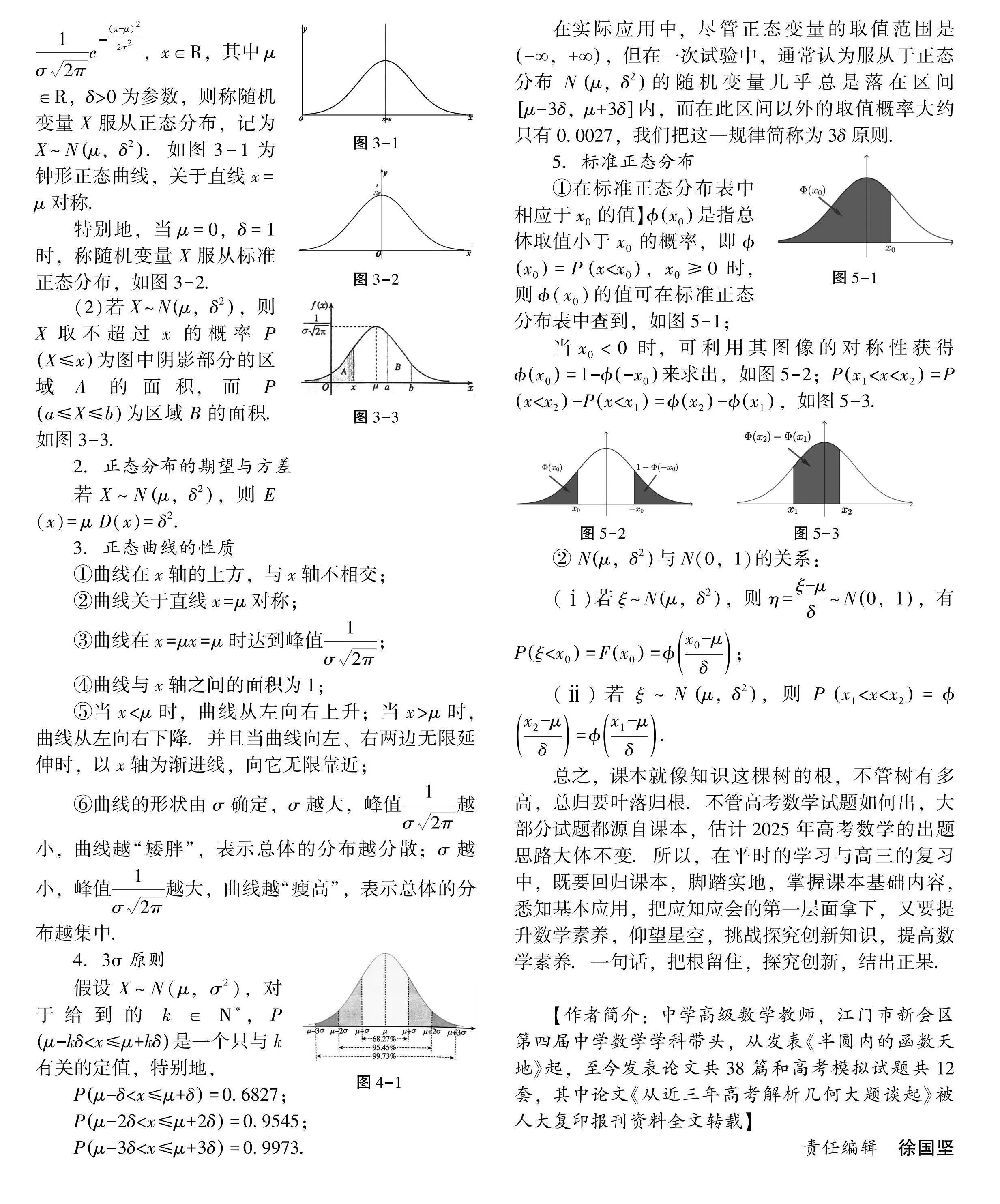
5．标准正态分布

①在标准正态分布表中相应于x0的值】x0是指总体取值小于x0的概率，即x0=Px<x0，x0≥0时，则（x0）的值可在标准正态分布表中查到，如图5－1；

当x0<0时，可利用其图像的对称性获得x0=1－－x0来求出，如图5－2；Px1<x<x2=Px<x2－Px<x1=x2－x1，如图5－3．

图5-2图5-3

② Nμ，δ2与N（0，1）的关系：

（ⅰ）若ξ～Nμ，δ2，则η=ξ－μδ～N0，1，有Pξ<x0=Fx0=x0－μδ；

（ⅱ）若ξ～Nμ，δ2，则Px1<x<x2=x2－μδ=x1－μδ．

总之，课本就像知识这棵树的根，不管树有多高，总归要叶落归根．不管高考数学试题如何出，大部分试题都源自课本，估计2025年高考数学的出题思路大体不变．所以，在平时的学习与高三的复习中，既要回归课本，脚踏实地，掌握课本基础内容，悉知基本应用，把应知应会的第一层面拿下，又要提升数学素养，仰望星空，挑战探究创新知识，提高数学素养．一句话，把根留住，探究创新，结出正果．

【作者简介：中学高级数学教师，江门市新会区第四届中学数学学科带头，从发表《半圆内的函数天地》起，至今发表论文共38篇和高考模拟试题共12套，其中论文《从近三年高考解析几何大题谈起》被人大复印报刊资料全文转载】

责任编辑 徐国坚