基于核心素养的小学数学“教—学—评”一体化研究

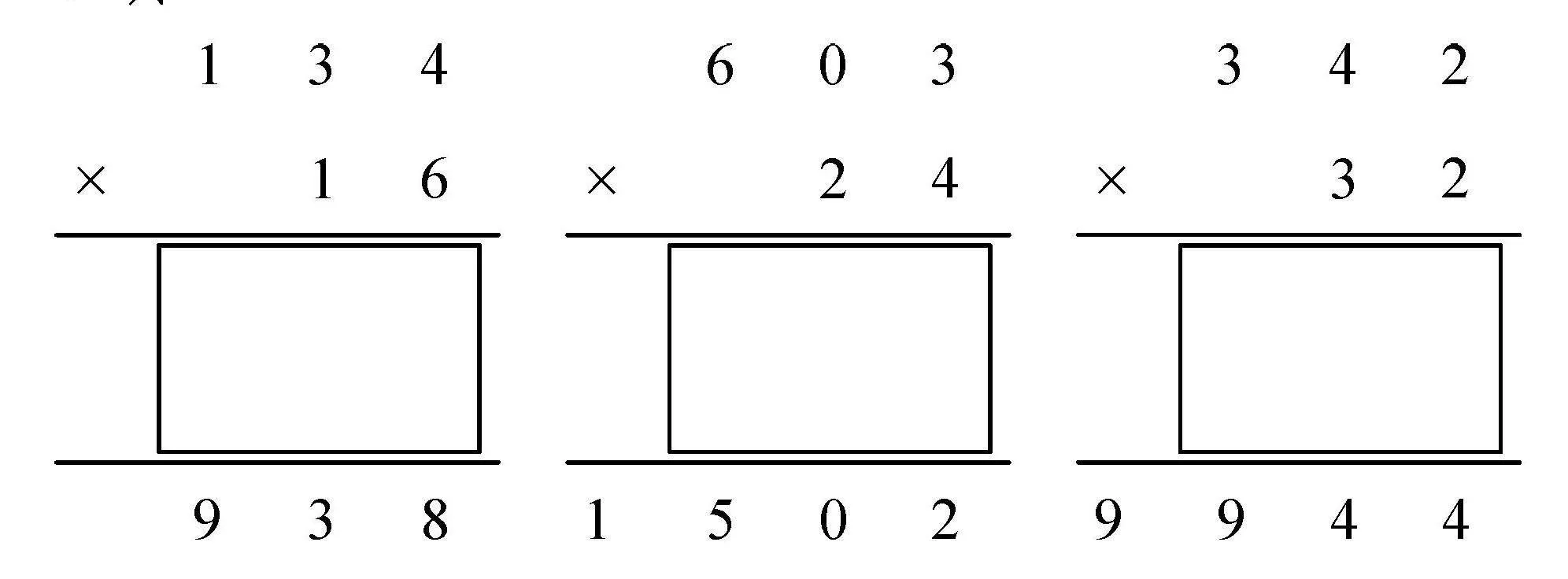
摘 要：

新课标明确提出了“教—学—评”一体化的要求，并予以细致指导.在此背景下，如何以数学核心素养为导向，基于学业质量标准，落实“教—学—评”一体化成为中小学教学改革的重点，也对一线教师提出了新的要求和挑战.本文构建了核心素养导向的小学数学“教—学—评”一体化设计工具，旨在为教师落实“教—学—评”一体化理念提供工具帮助.

关键词：核心素养；小学数学；“教—学—评”一体化；数与算数

《义务教育数学课程标准（2022年版）》

（以下简称“新课标”）

背景下，“教—学—评”一体化旨在以目标为导向确定评价标准，指导教师的教与学生的学.在此背景下，本文以小学数学“数与运算”知识点教学为例，开展核心素养导向的小学数学“教—学—评”一体化研究，助力以数学核心素养为依据的学习目标的确定、评价标准的制定以及教学活动的设计，将数学核心素养的形成和发展贯穿教学始终，将数学核心素养的培养落到实处.

1 创设情境，导入新课

问题1 今年暑假，老师去领略了一番青藏铁路的壮观.我从福州市出发，先自驾到青海省西宁市，汽车行驶速度为65千米每小时 ，一共行驶了43小时.我想知道从福州市到西宁市一共行驶了多少距离？

生：65×43.

师：为什么用乘法？

生1：因为汽车行驶的速度是每小时65千米，一共行驶了43小时，也就是求43个65是多少，所以用乘法.

生2：65是汽车行驶的速度，43小时是汽车行驶的时间，要求总路程就用速度乘时间.

学生独立计算后，教师利用投影仪展示学生的答案.

问题2 到达西宁市后，老师再从西宁市出发，乘坐青藏铁路线，一路向西，到达拉萨市.列车运行速度为145千米每小时、列车行驶时间为21小时.请大家列式求出总路程.

生：145×21.

【设计意图】新课程改革倡导“真情境”“真问题”.教师在数学教学时应将问题置于真实情境中，以真实的生活情境唤起学生的生活经验，以学科情境唤起学生的认知基础，使学生在面对富有挑战性的问题情境时，整体调用已有知识、经验、思想与方法.学生经历问题求解、探究发现的过程，建立对新知的理解.［1］因此，在本节课的教学设计中，笔者创设了从福州市到拉萨市旅游的问题情境，既帮助学生回忆了“两位数乘两位数”的计算方法，又引出了本节将要学习的“三位数乘两位数”，为学生比较两者的异同并实现知识迁移提供了支架.

教学评价：本环节的设计旨在帮助学生在复杂的问题情境中提取与问题相关的数学信息，培养学生的数学信息素养和“用数学的眼光观察”的能力.相比于教材中的例题，该问题情境蕴含的数学信息较多，学生需要将汽车和列车的速度与时间区分开并进行对应.从教学效果来看，学生在本环节的目标达成度较高.

2 理法交融，培养运算能力

2.1 竖式计算

师：145×21如何计算？具体步骤是怎样的？

生：第一步，用21的个位1乘145，等于145，求的是1个小时行驶了145千米；第二步，用21的十位2乘145，等于290，求的是20个小时行驶了2900千米；最后一步，把两层积相加，得到3045，求的是21个小时一共行驶的距离.

师：这里的145和290分别表示什么？

生：145表示的是145个一，末位对齐个位，290表示的是290个十，末位对齐十位.

2.2 算法多样

师：除了竖式计算，还有哪些计算方法？

生1：将竖式计算转化为求大长方形面积（如图1）.上面大长方形的面积是145乘20，与竖式计算中第二层积计算的是一样的，下面小长方形的面积是145乘1，与乘法竖式中第一层积表示的算式是一样的.两个长方形的面积之和等于整个大长方形的面积，就相当于我们在乘法竖式中把两层积加起来.

图1

生2：用“表格法”，每一格的乘积对应其中一部分结果，最后把每一格的得数加起来就是最终的得数（见表1）.

表1

100405

2020008001002900

1100405145

21008401053045

生3：第三种方法有点不一样，把21变成3×7，将三位数乘两位数转化成三位数乘一位数.145×21=145×3×7=435×7=3045.

生4：第三种方法和第一种方法类似，都是把21进行拆分.第一种方法是将21拆成整十数和个位数，第三种方法是拆成两个数相乘.

师：这两种方法之间有怎样的联系？

生1：这些方法都是把乘数进行拆分，只不过拆分的方式不同，有的拆成两个数相加，有的拆成两个数相乘，但是最后都要把各部分加起来.

生2：我们刚才学的竖式计算也是这样，列竖式计算是把第二个乘数拆成整十数和个位数，再分别去乘第一个乘数的每一个数，最后再把结果加起来.

生3：不管哪种方法，都是先拆分，再合起来.

2.3 对比类推，算法迁移

师：如果是三位数乘三位数，如“145×121”，算法有什么区别？

生：多一步用百位上的1去乘145，最后把三次的乘积加起来.

师：三位数乘两位数是把两次的乘积加起来，三位数乘三位数是把三次的乘积加起来.在计算时，用百位上的数去乘，得到的积就表示几个什么？

生：表示几个百.

师：以此类推，四位数乘四位数怎么计算？有什么变化？

生：四位数乘四位数要乘四次，第四次是用千位上的数字去乘，表示几个千.

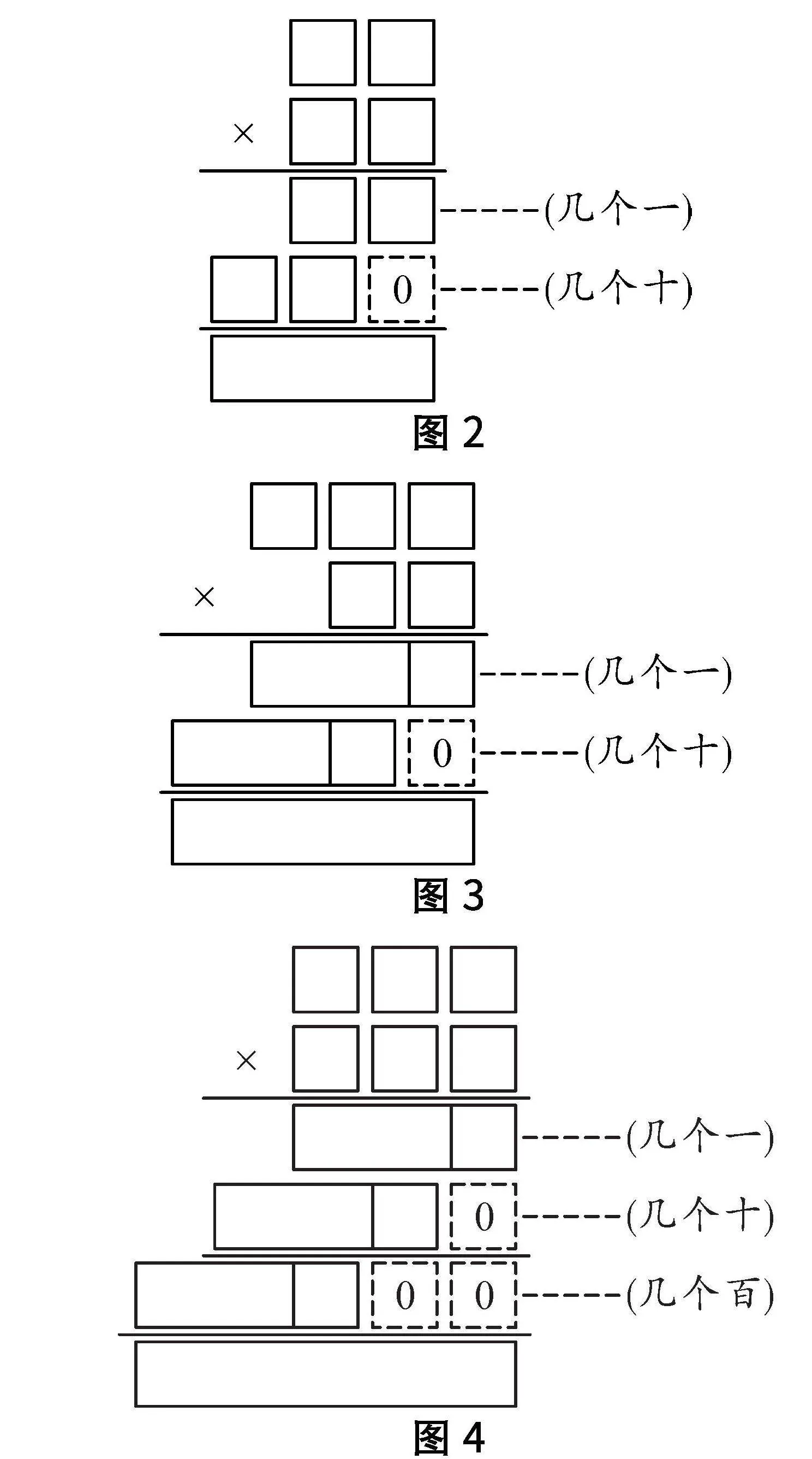
教师结合学生回答，在 PPT 上逐步出示如下乘法模型（如图2、图3、图4）.

图2

图3

图4

□□×□□

□□□

【设计意图】学生对算理算法的理解程度对其运算能力的形成和发展具有重要作用.本环节的设计旨在通过多种算法引导学生发现算法和算理内在的“一致性”，深化其对算理算法的理解.［2］同时，教师在引导学生观察对比的过程中，帮助学生逐步建立乘法模型.

教学评价：本环节的教学旨在帮助学生理解竖式中

每一步计算的是什么，表示什么含义.教学时，教师结合“面积图法”与“表格法”帮助学生厘清算理并将“三位数乘两位数”的算法扩展到“多位数乘多位数”，使学生建立乘法模型.在教学过程中，大部分学生虽然明白算理，但是无法用数学的语言逻辑清晰地表示出来.对此，教师在教学过程中应及时调整教学进度，通过不断地追问、引导，带领学生逐渐建立“乘法模型”.

3 巩固练习，深化算理理解

（1）计算140×20.

生：这道题可以直接口算14×2或2×14，最后再把末尾的两个“0”添上.

师：如果列成竖式，有什么办法？具体计算过程是怎样的？

生：列式时先不看末尾的两个“0”，算出14×2=28，然后再添上末尾的两个“0”，就等于2800.

师：列式计算时，为什么可以先不看末尾的两个“0”？

生：因为“0”乘任何数都等于“0”.

（2）计算104×23.

师：如果把末尾的“0”放在乘数的中间，变成“104×23”，计算过程是怎样的？

生：第一步先算“3×104”.

师：第二步用23十位上的2乘104，这个“2”代表的是什么？

生：两个十.

师：算出来等于208，这里的208表示的是208个什么？

生：表示208个十，所以最后等于2392.

师：在计算时如果没有进位的情况，要怎样处理？

生：写上“0”占位.

【设计意图】乘数中间、末尾有“0”的两类算式作为“三位数乘两位数”教学中的两类特殊计算，教学重点有所区别.对于乘数末尾有“0”的乘法，希望学生能在口算的基础上探究竖式的简便算法并理解末尾“0”不参与运算的原理；对于乘数中间有“0”的乘法，则重在对比有进位时和没有进位时的情况.

教学评价：本环节的教学希望学生能根据“数的意义”解释为什么在计算的过程中可以先不计算末尾的“0”，并借助乘数末尾有“0”的乘法竖式计算理解乘法运算的本质是“计数单位”个数的运算.在计算“末尾有‘0’”的乘法时，有三分之一的学生不知道在计算时可以先不将末尾的“0”参与运算，剩余的三分之二学生虽然知道简便算法，但都认为是因为“0”乘任何数都得“0”，所以可以先不参与计算，未涉及算理层面.针对学生的表现，教师从“计数单位”的角度予以解释.

4 辨析反思，培养估算能力

不计算，快速判断这三道竖式计算题结果是否正确.

134×16

938

603×24

1502

342×32

9944

生：第一道题肯定错，因为积不可能是三位数.

师：三位数乘两位数的积不可能是三位数，那三位数乘两位数的积可能是几位数？

生：可能是四位数，也可能是五位数

师：有没有可能是六位数？

生：没可能.最大的三位数是999，最大的两位数是99，即使都把它们往大估算，1000×100=100000，乘积是最小的六位数，所以三位数乘两位数的积最大只可能是五位数.

师：那最小呢.

生：最小的三位数是100，最小的两位数是10，100×10=1000，所以三位数乘两位数的乘积最小是1000.

师：同学们说得都很清晰，借助计算器，我们知道刚才同学说的999×99=98901，所以我们可以确定三位数乘两位数的乘积一定在什么之间？

生：1000～98901之间.

师：除了根据乘积的位数来判断，我们还有什么方法可以直接判断计算结果是否正确？

生1：可以用估算的方法.把603估成600，把24估成20，600×20=12000，因为两个乘数都是往小估了的，所以结果一定比12000大，所以第二题肯定是错的.

生2：也可以用看个位的方法.比如第一题，4×6=24，所以积的末尾一定是4.

【设计意图】估算活动是促进学生数感发展的重要途径，估算涉及对数字大小的理解能力以及修正调整数字的能力等.因此，在本课的教学过程中，教师设计“辨析反思”学习任务，引导学生在不计算的情况下，对“三位数乘两位数”的积做出合理估算，旨在培养学生的估算能力，进而促进学生数感的发展.［3］

教学评价：在本环节的教学过程中，学生除了提出根据乘积的位数以及末位数字判断计算结果是否正确外，还提出了利用“大、小估”的方式估计乘积的合理范围，进而做出判断，说明学生在本轮的学习中能够有意识地进行估算且具备一定的估算能力.在介绍估算思路的过程中，学生能够较为清晰地表达自己的思考过程，教学效果较好.

5 渗透文化，促进融会贯通

师：不同的国家在计算乘法算式时有不同的计算方法.让我们通过一节数学微课，探究中国古代的“画线法和算筹法”以及意大利的“格子算法”计算原理.

生1：这些方法只是写法不一样，形式不一样，道理却是一样的.

和竖式一样，都是用一个乘数的每一位去乘另一个乘数的每一位，都要“满十进一”.

师：乘法计算的方法还有很多，除了我们今天学习的竖式计算，以及微课中介绍的格子算法、算筹法和画线法之外，古埃及还有倍乘法，古印度、意大利还有竖式乘法.虽然方法不同，但是它们的道理都是一样的，感兴趣的同学课后可以用这些方法进行尝试，并探索其他与众不同的计算方法.

【设计意图】本环节教师除了为学生提供教材中有关意大利“格子算法”的数学微课，还为学生提供了中国古代的“画线法”与“算筹法”，通过多种方法的对比，帮助学生发现乘法计算本质上的共通之处，激发学生对数学文化的中国自信，鼓励学生在前人的基础上进行大胆创新.

教学评价：本环节设计希望学生通过数学文化的学习，建立起对数学文化的中国自信，激发对数学学习的兴趣与热爱.在教学过程中，“数学微课”的形式对四年级的学生有着较大的吸引作用，课堂上学生的注意力集中、兴奋度高.

6 结语

核心素养导向的小学数学“教—学—评”一体化教学设计能够促进学生数学核心素养形成与发展.在“教—学—评”一体化的设计中，学习目标始终发挥着“统领”作用，决定评价标准的制定以及教学活动的设计.以核心素养为导向的小学数学“教—学—评”一体化教学无论是在确定学习目标、制定评价指标还是设计教学活动中，都始终以核心素养为导向，将核心素养的培养贯穿始终.

参考文献

［1］黄燕萍.基于核心素养的小学数学统计与概率“教—学—评”一体化研究［J］.教育界，2024（16）：53-55.

［2］李娟.探究“教—学—评”一体化课堂促进学生核心素养发展——以小学数学学科为例［J］.试题与研究，2024（3）：28-30.

［3］温海澍.核心素养导向下小学数学“教—学—评”一体化教学评价探索——以人教版数学五年级下册“长方体、正方体的认识”教学为例［J］.广西教育，2023（22）：54-58.