机翼前缘蜂窝夹层结构力学性能分析

摘 要：研究机翼前缘蜂窝夹层结构在上翼面均布气动载荷作用下的力学性能。首先给出蜂窝夹层结构芯层等效弹性参数，用修正后的Gibson模型，将离散蜂窝芯结构按照力学等效的原则转化为均质的三维正交各向异性材料；然后用内聚力单元对蜂窝芯和面板之间的胶接界面进行建模，用壳单元对碳纤维增强复合材料面板进行建模；最后，利用有限元方法，对整个蜂窝夹层结构进行力学性能分析，显示了蜂窝芯和复合材料面板之间的剥离过程，对蜂窝芯和面板剥离破坏模式以及复合材料面板损伤破坏模式进行了分析。

关键词：蜂窝夹层结构；等效弹性常数；破坏模式；有限单元法；内聚力单元

中图分类号：V214.6" " " " " " " 文献标识码：A" " " " " " "文章编号：1007 - 9734 （2024） 05 - 0013 - 07

DOI：10.19327/j.cnki.zuaxb.1007-9734.2024.05.002

0 引 言

蜂窝夹层结构与一般的层合板结构相比，具有抗弯刚度高、热膨胀系数小、吸音、吸波、气动表面光滑等诸多优点，被广泛应用于机翼前缘、机舱地板、轻型通用飞机的主次承力结构、卫星结构和高速列车制造中[1-3]。对结构进行分析时，现在常用的大型商业有限元软件中没有蜂窝夹层结构的材料库。必须对结构进行等效处理，即将夹层结构中离散的蜂窝折算成等效的连续体，将夹芯层等效成一层三维各项异性材料，把它看作层合板的一个特殊单层。

早在1969年，Allen等人[4]对夹层结构早期的试验和分析方法做出了巨大贡献。对于蜂窝夹层结构的宏观力学行为，很多国内外学者提出了各种简化模型和计算理论。在常用的计算模型中，位移模型理论应用最广[5-7]。Gibson 等[8]在1982年利用等壁厚正六边形蜂窝模型，建立了在剪切载荷和面内拉压载荷作用下蜂窝结构的变形模式，并给出了各等效弹性参数的计算公式。王颖坚等[9]通过对Gibson的方法进行修正，建立了满足平衡条件的等壁厚蜂窝和非等壁厚蜂窝结构在面内剪力作用下的变形模式，并根据新建立的变形模式导出了新的计算公式，计算结果与实测结果相符。由于Gibson公式忽略了蜂窝壁板伸缩变形的刚度，导致对结构进行数值分析时夹芯层材料的弹性矩阵表现出不确定性。针对这一问题，富明慧等[10]考虑了蜂窝壁板的弯曲变形和伸缩变形对面内刚度的影响，对Gibson公式进行了修正。所得结果不但克服了Gibson公式面内等效泊松比不合理的缺陷，同时还提出了考虑夹芯层面内刚度的一种简化方案。

蜂窝夹层结构在拉压、剪切载荷作用下的主要失效模式分为总体失效和局部失效。局部失效主要包括蜂窝失效、面板失效和胶接界面失效。赖士洪等[11]在1989年通过一系列的剥离试验分析了胶粘剂的剥离强度与蜂窝夹层结构剥离破坏模式的关系，提出了蜂窝芯粘接边强度的概念。张广成等[12]通过实验发现，当有胶层存在时，结构的剥离强度明显增大。当蜂窝芯和面板之间无胶层时，破坏始终发生在蜂窝芯和面板的胶接面上。Shen 等[13]以不锈钢点阵结构为芯材的夹层结构作为研究对象，通过准静态到动态的加载，研究结构的层间断裂韧性，通过夹芯梁的三点弯曲试验测得结构面板和芯材之间的分层性能。

本论文主要研究蜂窝夹层结构面板和蜂窝芯之间的胶接界面力学性能和面板失效问题。建立蜂窝、复合材料面板、粘接界面的有限元模型，应用有限元软件计算、分析结构的强度，预测面板和蜂窝芯的剥离，复合材料面板的失效等情况，展示蜂窝夹层结构内部的损伤发展过程。

1 蜂窝夹层结构芯层弹性参数

1.1" 蜂窝芯层等效弹性参数的Gibson模型[8]

对蜂窝夹层结构应用有限元进行分析时，须对结构进行力学等效处理。先将蜂窝芯等效为一层三维正交各项异性层，把它作为层合板的一个特殊单层处理，将蜂窝芯等效为均质的正交各向异性层。对于二维正交各向异性材料，有如下的应力－应变关系：

[σxσyσxy=Dεxεyγxy，" D=E11-μ1μ2E1μ21-μ1μ20E2μ11-μ1μ2E21-μ1μ2000Gxy]（1）

式中，σx，σy为x和y方向的主应力，σxy为剪切应力，ɛx，ɛy为x和y方向的主应变，γxy为剪切应变，D为弹性矩阵，E1，E2为x和y方向的杨氏弹性模量，m1，m2为x和y方向的泊松比。另外，由于正交各向异性材料弹性矩阵的对称性，弹性常数应该满足关系式

[E1μ2=E2μ1] （2）

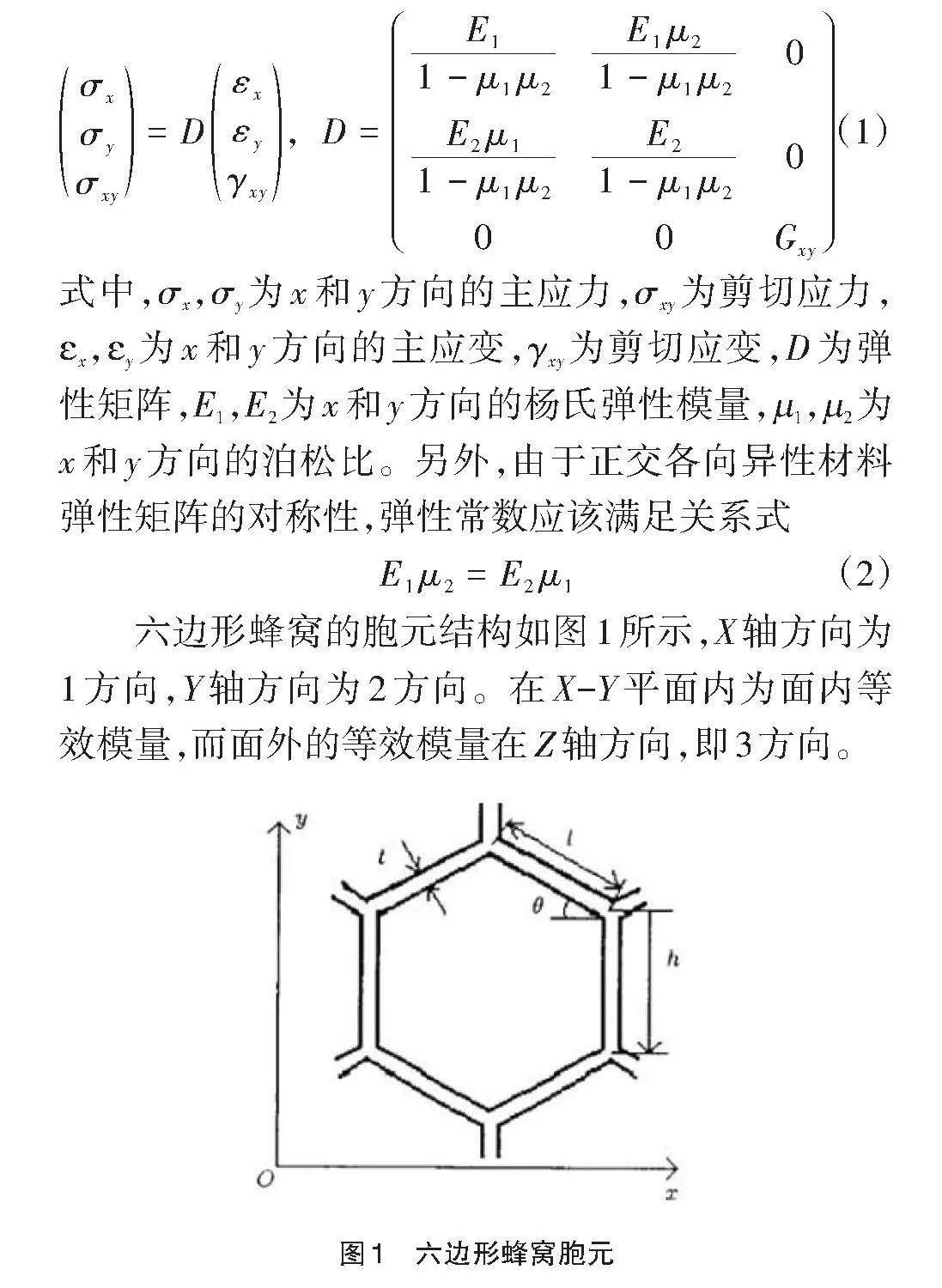
六边形蜂窝的胞元结构如图1所示，X轴方向为1方向，Y轴方向为2方向。在X-Y平面内为面内等效模量，而面外的等效模量在Z轴方向，即3方向。

图中，l为蜂窝胞元斜臂长度，h为直臂长度，t为胞壁厚度，θ为蜂窝特征角。

Gibson给出了图1中的面内等效弹性常数：

[E1=Est3l3cosθβ+sinθsin2θμ1=cos2θβ+sinθsinθE2=Est3l3β+sinθcos3θμ2=β+sinθsinθcos2θG12=Est3l3β+sinθβ22β+1cosθ] （3）

式中，Es为蜂窝基体材料的弹性模量［10］，β=h/l。对于正六边形蜂窝，h=l，β=1，θ=30o，则式（3）变为：

[E1=43Est3l3μ1=1E2=43Est3l3μ2=1G12=13Est3l3] （4）

从以上关系式可以看出，式（3）和式（4）明显符合式（2），而且两个泊松比满足，因此弹性矩阵D是奇异的，即通过式（3）和式（4）无法给出确定的弹性矩阵D。导致式（3）和式（4）无法直接使用，出现这一问题的原因是Gibson只考虑了蜂窝壁板的弯曲变形而未考虑其伸缩变形。由于蜂窝芯层受面板约束，其伸缩变形的刚度并非小到可以忽略。

1.2" 考虑蜂窝壁板伸缩变形的等效弹性参数

由于Gibson推出的等效公式有上述缺陷，所以无法为有限元分析提供准确的数据。必须对上述公式进行修正，考虑蜂窝壁板在面内力作用下的伸缩变形。对于正六边形蜂窝，h=l，β=1，θ=30o，考虑蜂窝壁板伸缩变形之后可以得到如下的等效公式：

[E1=43Es1-3t2l2t3l3μ12=1-4t2l2E2=43Es1-5t2l2t3l3μ21=1-83t2l2G12=13Est3l3] （5）

考虑面外等效弹性模量时，则有：

[E1=43Es1-3t2l2t3l3E2=43Es1-5t2l2t3l3E3=2γ3tl3Es，G12=3γ2tl3Gs，G13=3γ2tlGs，G23γ3tlGsμ12=1-4t2l2，μ13=E1E3μs，μ23=E2E3μs] （6）

式中：Gs为蜂窝基体材料的剪切模量；μs为蜂窝基体材料的泊松比；l为蜂窝胞元臂板长度；t为胞壁厚度；γ为修正系数，与蜂窝结构的制造工艺有关，一般取0.4—0.6。

观察式（6）可以发现，由于蜂窝结构的胞壁厚度t与蜂窝胞元臂长h相比尺寸很小，所以t与l的比值远小于1，导致蜂窝芯在面内具有很弱的正交各向异性。1方向的弹性模量略大于2方向的弹性模量，3方向的弹性模量远大于1方向和2方向的弹性模量，面外的剪切模量明显大于面内剪切模量。

1.3" 蜂窝芯层密度计算方法

蜂窝夹层结构的动力学性能与其密度密切相关，芯层的密度由蜂窝结构的各个参数决定，一般可用如下公式计算：

[ρ=23tlρs] （7）

式中：ρ为蜂窝芯层等效密度；ρs为蜂窝基体材料的密度。

2 蜂窝夹层结构的失效模式

蜂窝夹层结构在载荷作用下会出现不同形式的损伤破坏，如整体失稳、面板皱屈、剪切皱损等[14]。本文只考虑蜂窝芯与复合材料面板之间的剥离问题，以及复合材料面板的失效问题，即由于胶黏剂剪切强度不足，导致蜂窝芯和面板脱胶的剪切皱损问题和面板破裂问题。

2.1" 蜂窝芯和复合材料面板的剥离

在分析蜂窝夹层结构时，可以将蜂窝芯等效为一层连续的三维正交各向异性材料，把它看作复合材料层合板的一个特殊单层来处理。所以蜂窝芯和复合材料面板之间的剥离强度问题就转化为层合板两个单层板层间强度的问题。本文使用内聚力单元来模拟蜂窝芯和复合材料面板之间的胶层。当某一个或多个内聚力单元满足特定的应力或应变条件时，就可以认为在该处胶接界面失效。将失效的单元删除，即可模拟蜂窝芯和复合材料面板之间的剥离现象。

用有限元建模时，在蜂窝芯层和复合材料面板间定义一个新区域，用该区域模拟胶层，其主要作用是粘接复合材料面板和蜂窝芯。在这个粘接面上有三种作用力[15]：一个法向正应力σn和两个切向剪应力σs、σt。

本文采用双线性本构模型描述胶层界面的损伤扩展过程。如图2所示。

图中：δ0为单元刚度降阶的临界位移值；δ为当前加载过程中的有效位移；δmax为界面单元失效的临界位移值。

当δlt;δ0时，胶层界面处于线弹性阶段，未出现软化损伤。当δ=δ0时，损伤起始，胶层界面发生软化。当δ0lt;δlt;δmax时，胶层界面处于线性软化阶段。当δ=δmax时，层间开裂，材料完全失去承载能力。

2.2" 复合材料面板的损伤破坏

Hashin失效准则[16]可以准确预测各种不同的失效模式，包括纤维拉伸破坏、压缩破坏，基体拉伸破坏、压缩破坏等。对于本文中的复合材料面板的破坏，忽略其层间应力的影响，用二维Hashin准则对其损伤进行判定。二维Hashin失效准则如下：

纤维受拉破坏（[σ11≥0]）：

[Ftf=σ11Xt2+ατ12SL2] （8）

纤维受压破坏（[σ11lt;0]）：

[Fcf=σ11XC2] （9）

基体拉伸破坏（[σ22≥0]）：

[Ftm=σ22Yt2+τ12SL2] （10）

基体压缩破坏（[σ22lt;0]）：

[Fcm=σ222ST2+Yc2ST2-1σ22Yc+τ12SL] （11）

式（8）-（11）中：SL为纵向剪切强度；ST为横向剪切强度；α为系数，表征剪应力对纤维拉伸破坏的贡献程度；[σ11，σ22，τ12]为有效应力分量。只要各应力分量满足式（8）-（11）中的任意一个，就认为材料发生了相应的破坏。

3 蜂窝夹层机翼前缘结构力学性能有限元分析

3.1 机翼前缘结构有限元建模

图3为蜂窝夹层机翼前缘结构示意图，该结构由外侧复合材料面板、蜂窝芯和内侧复合材料面板三部分组成，复合材料面板和蜂窝芯由胶层粘接在一起。

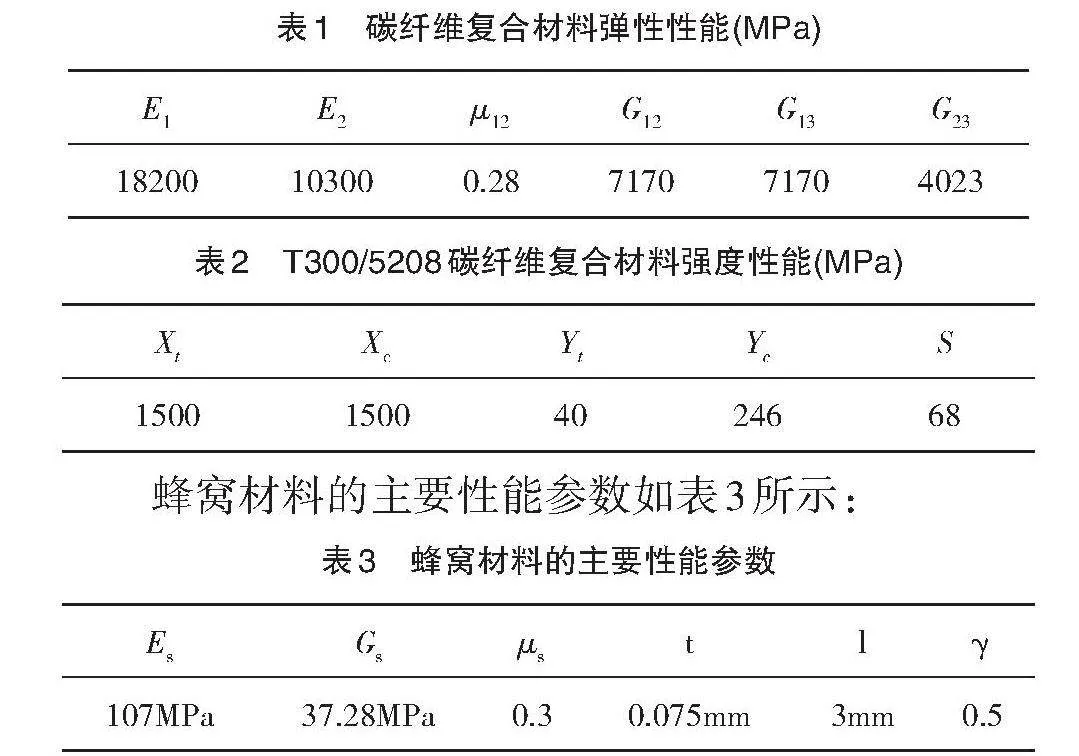
结构有限元模型中，面板由T300/5208碳纤维增强复合材料单向板铺设而成，蜂窝材料参数参考文献[17]选取。表1为T300/5208碳纤维增强复合材料的弹性性能参数，表2为T300/5208的强度性能参数。

蜂窝材料的主要性能参数如表3所示：

商业有限元软件对蜂窝夹层结构进行力学性能分析时，由于软件中没有蜂窝结构的材料库，所以必须对蜂窝进行力学等效处理，将其等效成一层特殊的、均匀的、各向异性的单层材料。将表3中的值带入式（6），可得蜂窝芯层的等效弹性参数，如表4所示：

本文采用ABAQUS中的孤立网格技术，先对蜂窝芯层划分网格，将其划分为三维8节点线性实体单元C3D8R，共计1782个单元。然后在已经划分单元的蜂窝芯内外侧各偏移出一层8节点三维内聚力单元COH3D8。这两层实体单元模拟蜂窝芯和复合材料层合板之间的粘接胶层，厚度均为0.1mm。

图4为蜂窝芯层等效材料及有限元网格示意图。将蜂窝芯等效为三维正交各向异性实体材料，将表4中的蜂窝材料工程常数赋给这一单层，这样就将整个蜂窝芯层看作由一层单向板铺设而成的铺层。采用离散坐标系，材料的3方向为蜂窝芯层曲面的外法线方向，1方向为沿着机翼前缘蜂窝芯的长度方向，于是2方向可按右手螺旋法则确定。

图5为外侧面板的铺层信息及有限元网格。覆盖在蜂窝芯层上的外侧碳纤维增强复合材料面板的铺层信息为[0/45/90/0/90/-45/0]，共7层，单层厚度为0.25mm，每一层材料的参数如表1和表2所示。

图6为内侧面板的铺层信息及有限元网格。内侧碳纤维增强复合材料面板的铺层信息为[0/90/90/0]，共4层，单层厚度为0.25 mm，每一层材料的参数如表1和表2所示。铺层同样采用离散坐标系，材料的3方向为内侧面板的外法线方向，1方向为长度方向。

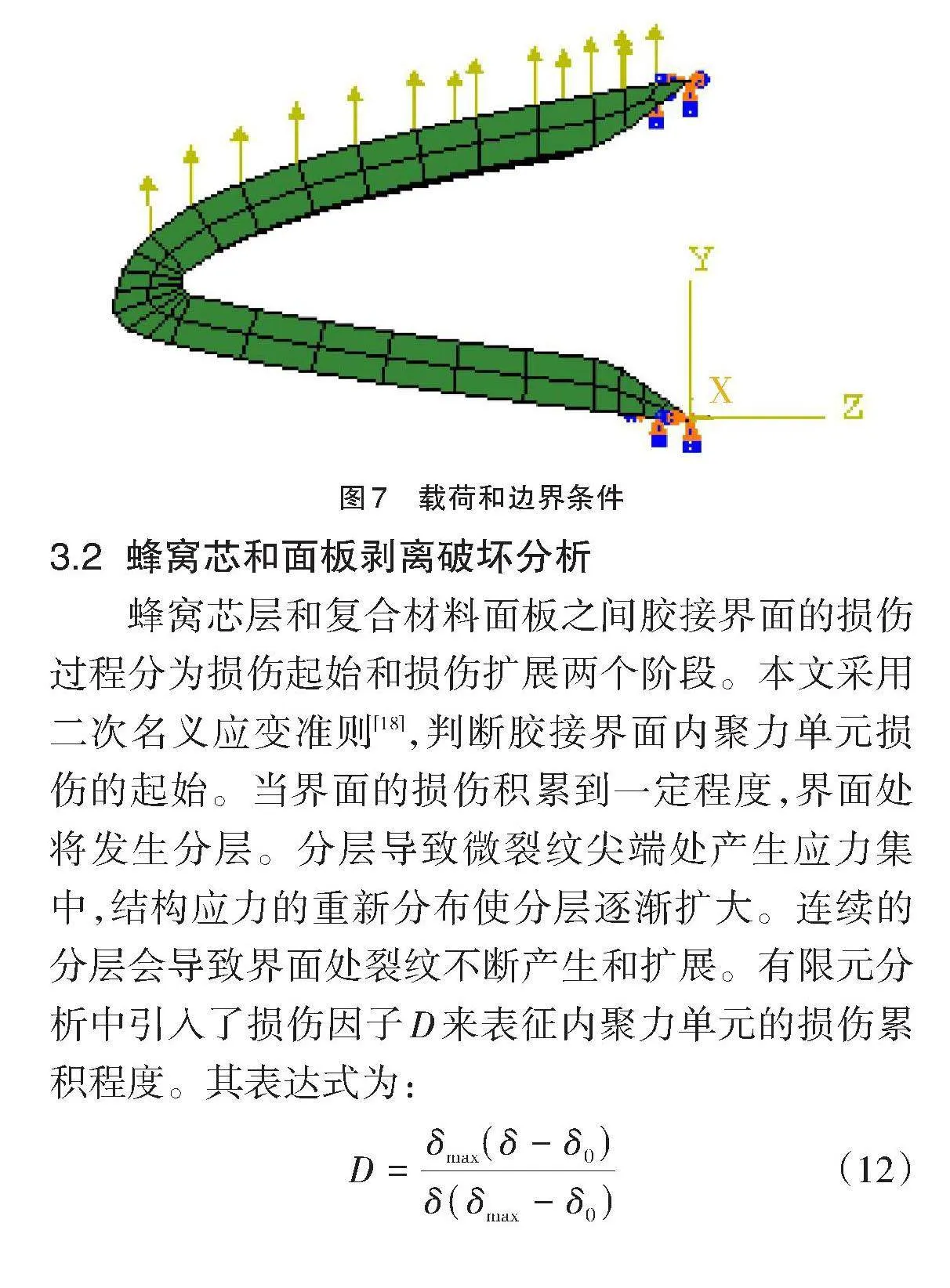
对机翼前缘结构的各个部分分别给定材料属性之后，按照图7所示施加载荷和边界条件。载荷作用区域共有374个节点，在每个节点上施加Y轴正方向的力，用以模拟施加在机翼前缘的均布气动载荷。

3.2" 蜂窝芯和面板剥离破坏分析

蜂窝芯层和复合材料面板之间胶接界面的损伤过程分为损伤起始和损伤扩展两个阶段。本文采用二次名义应变准则[18]，判断胶接界面内聚力单元损伤的起始。当界面的损伤积累到一定程度，界面处将发生分层。分层导致微裂纹尖端处产生应力集中，结构应力的重新分布使分层逐渐扩大。连续的分层会导致界面处裂纹不断产生和扩展。有限元分析中引入了损伤因子D来表征内聚力单元的损伤累积程度。其表达式为：

[D=δmaxδ-δ0δδmax-δ0] （12）

当D=0时，表示胶接界面层还未屈服或刚开始屈服。当0lt;Dlt;1时，表示材料内部出现损伤，胶层开始软化，D=1时材料发生破坏。本文用内聚力单元形心处的损伤因子D表征单元的损伤程度。

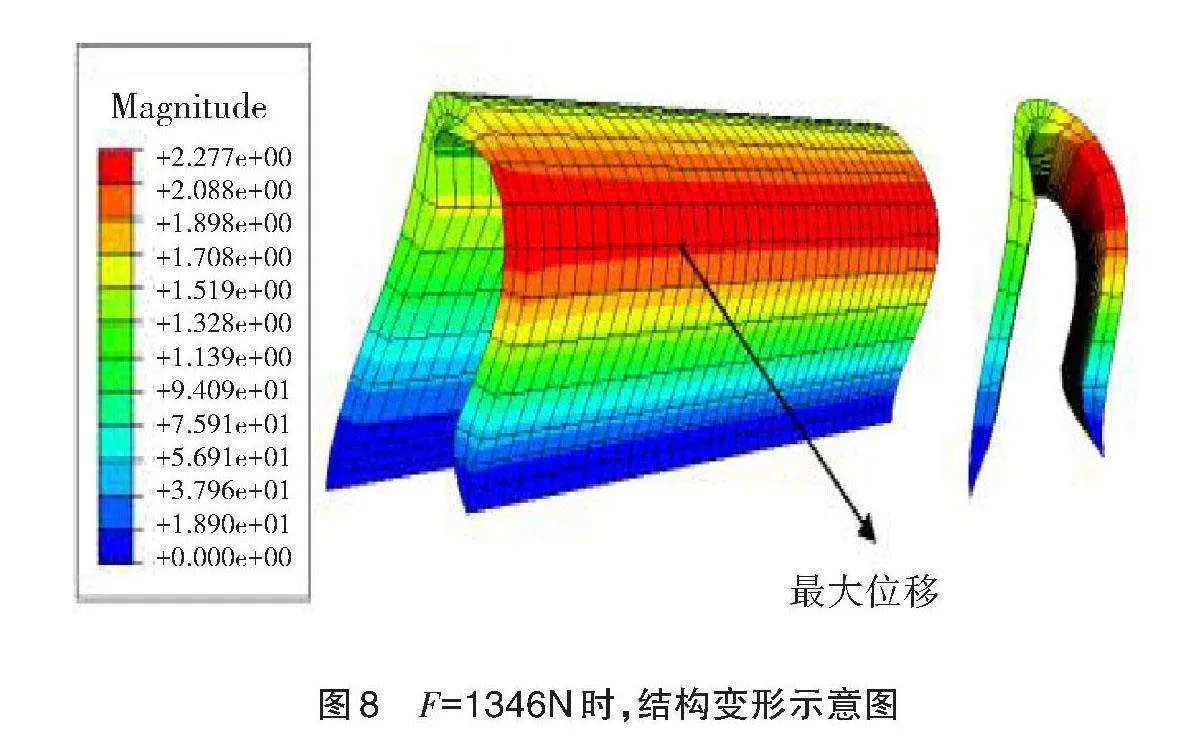
通过有限元逐步施加载荷，当总的气动力Flt;1346N时，连接内侧复合材料面板和蜂窝芯的内侧胶层处于线弹性阶段，D=0。当气动载荷F=1346N时，内侧胶层开始屈服，发生软化损伤，屈服部位的单元损伤因子D=8.36✕10-4。而外侧面板和蜂窝芯之间的外侧胶层依然保持完好，材料仍处于线弹性阶段，D=0。此时机翼前缘结构变形如图8所示，可见结构的最大位移（毫米）出现在前缘结构上翼面位置。

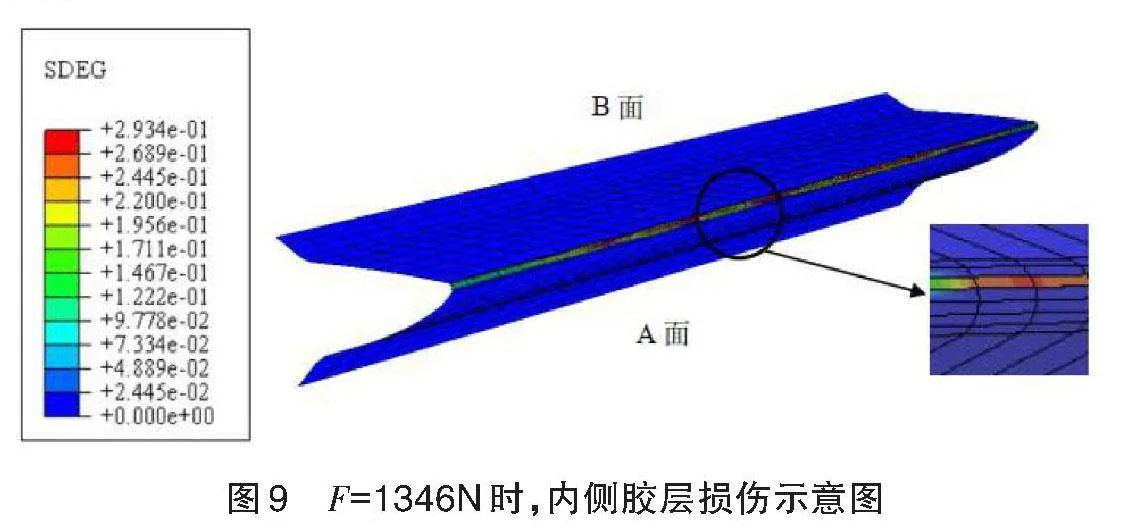
图9为当F=1346N时，结构中连接内侧复合材料面板和蜂窝芯的内侧胶层的软化损伤区域示意图。

观察图9可知，内侧复合材料面板和蜂窝芯之间的胶接区域最先出现损伤。损伤区域出现在A、B面的交接处。在这一区域胶层的上表面与蜂窝芯相连，下表面与内侧复合材料面板相连。由于两者的刚度相差很大，导致在外力作用下蜂窝芯和复合材料面板之间的胶层受到较强的剪切作用。当单元的应变满足二次名义应变准则时，材料开始发生屈服。虽然该胶层局部区域发生屈服（软化），但是还未发生破坏。因此结构仍保持完好，可继续承载。

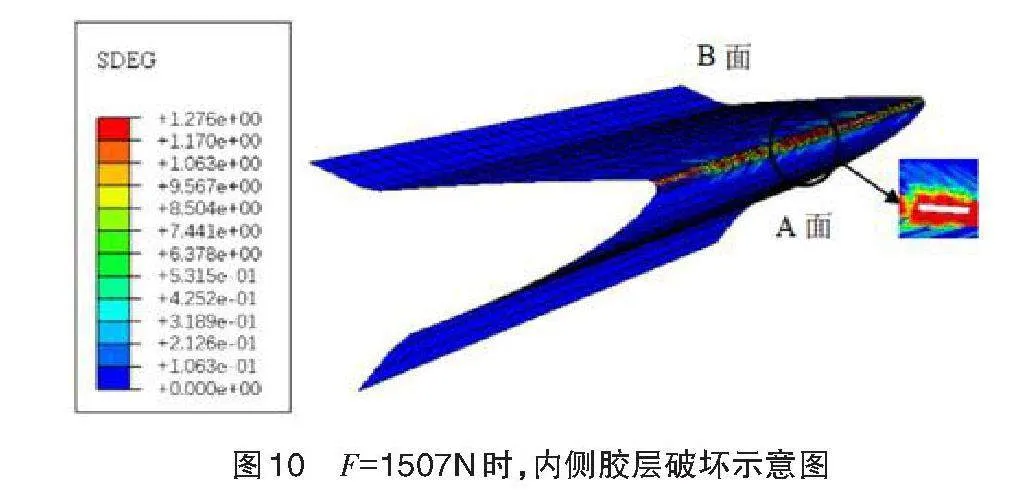
随着载荷进一步增大，内侧面板和蜂窝芯之间的损伤区域将逐渐增大。当气动载F=1507N时，单元的应变能达到内聚力单元应变能释放率的临界值，内侧胶层开始出现破坏。破坏面积SD=302mm2，约占内侧胶层总面积的0.72%。内侧面板和蜂窝芯出现剥离现象，如图10所示。

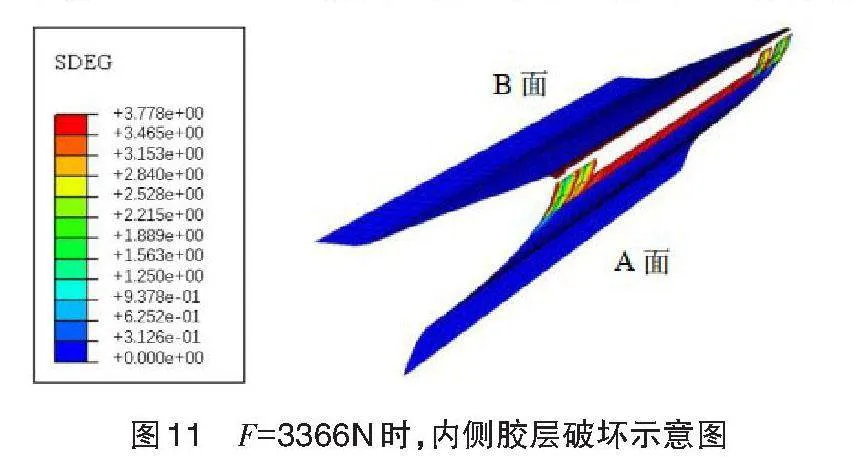
当F=3366N时，内侧胶层A、B面交界段处被彻底破坏。然后破坏区域迅速向A面扩展，蜂窝芯和内侧复合材料面板之间出现大面积剥离，破坏面积达到SD=18068mm2，占内侧胶层总面积的4.61%，如图11所示。此时连接外侧复合材料面板和蜂窝芯的外侧胶层还处于线弹性阶段，未出现软化损伤。

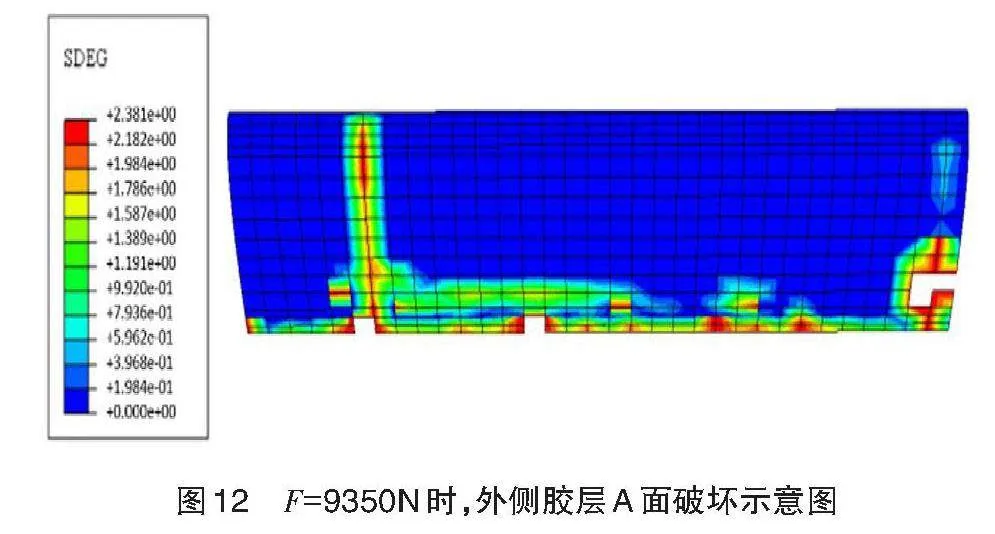
F=9350N时，外侧胶层在A面靠近固支端的区域和前缘根部发生破坏。损伤区域在整个外侧胶层的A面扩展，如图12所示。

3.3" 机翼前缘结构复合材料面板损伤破坏分析

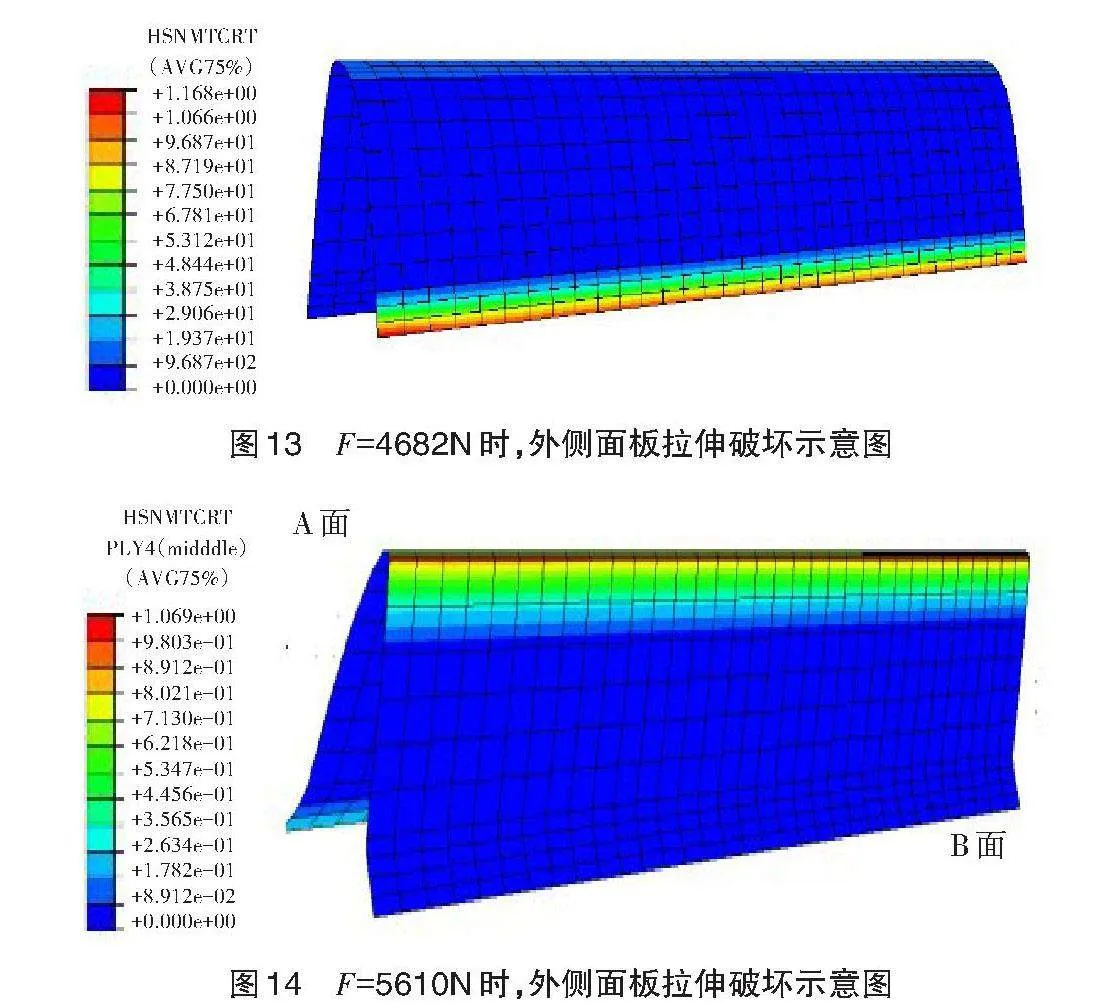
当气动载荷F=4862N时，机翼前缘结构外侧复合材料面板发生破坏。破坏主要出现在机翼前缘结构外侧复合材料面板A面靠近固支端的部位，如图13所示，该部位铺层发生严重的基体拉伸破坏，最先破坏的是第1层即0°纤维铺层，该铺层靠近蜂窝芯。而内侧复合材料面板并未发生破坏。

当F=5610N时，内侧复合材料面板的第4层即0°铺层出现基体拉伸破坏。损伤出现在内侧面板B面靠近A、B面交界的区域，如图14所示。

在以上加载过程中，未出现纤维拉伸破坏、纤维压缩破坏和基体压缩破坏模式。

4 结 论

本文主要对机翼前缘蜂窝夹层结构进行有限元建模和力学性能研究，模拟当结构上翼面受均布气动载荷作用时，蜂窝芯和复合材料面板之间的剥离现象。

从以上分析可以看出，若不考虑蜂窝芯层的破坏，结构在气动外载荷作用下的损伤主要出现在碳纤维增强复合材料面板和蜂窝芯之间的胶接界面上。其中蜂窝芯和内侧复合材料面板之间的胶接界面最先出现破坏，结构的完整性被破坏，承载能力开始下降。随着载荷的增加，损伤区域扩大，外侧复合材料面板和蜂窝芯之间的胶接界面也出现破坏，结构刚度进一步降低。如果再增大载荷，胶接区域的破坏面积迅速扩展，复合材料面板最终将和蜂窝芯发生剥离，结构失去承载能力。外侧纤维增强复合材料面板在载荷作用下先出现的破坏模式主要为基体拉伸破坏。当载荷进一步增大时，内侧复合材料面板也出现基体拉伸破坏。

参考文献：

［1］M AMRAEI，M SHAHRAVI，Z NOORI，et al.Application of Alu-minum honeycomb sandwich panel as an energy absorber of high-speed train nose［J］.Journal of Composite Materials，2014，48（9）：1027-1037.

［2］程文礼，袁超，邱启艳，等.航空用蜂窝夹层结构及制造工艺［J］.航空制造技术，2015（7）：94-98.

［3］柳敏静，武湛君.复合材料蜂窝夹层结构在飞机中的应用［J］.科技导报，2016，34（8）：21-25.

［4］ALLEN G.Analysis and design of structural sandwich panel［M］. Oxford UK： Pergamon Press，1969.

［5］E REISSNER.Finite deflection of sandwich plates［J］.Journal of Aerospace Science，1948，15（7）：435-440.

［6］H J HOFF.Bending and buckling of rectangular sandwich plates ［J］.NASA TN，1950：2225.

［7］杜庆华.三合板的一般弹性理论［J］.物理学报，1954，10（4）：395-411.

［8］L J GIBSON，M F ASHBY，G S SCHAJER.The mechanics of two-dimensional cellularmaterials［J］.Proc. R. Soc. Lond， 1982，A382：25-42.

［9］王颖坚.蜂窝结构在面内剪力作用下的变形模式［J］.北京大学学报（自然科学版），1991，27（3）：301-307.

［10］富明慧.蜂窝芯层的等效弹性参数［J］.力学学报，1999，31（1）：113-117.

［11］赖士洪，唐发伦，邹贤武.胶接铝蜂窝结构的剥离破坏分析［J］.航空材料，1989，9（3）：22-28.

［12］张广成，赵景利.蜂窝夹层结构复合材料的力学性能研究［J］.机械科学与技术，2003，22（2）：280-282.

［13］YI-OU SHEN，WESLEY CANTWELL，YAN LI.Skin-core adhesion in high performance sandwichstructures［J］.Jour-nal of Zhejiang University-SCIENCE A（Applied Physics amp;Engineering），2014，15（1）：61-67.

［14］芦颉.金属蜂窝芯结构的疲劳行为研究［D］.哈尔滨：哈尔滨工业大学，2011.

［15］滕锦，李斌太，庄茁.Z-pin 增韧复合材料层合板低速冲击损伤过程研究［J］.工程力学，2006，23（1）：209-216.

［16］Z HASHIN.Failure criteria for unidirectional fiber com-posites［J］.Journal of AppliedMechanics，1980，47：329–334.

［17］梁海州，张元龙.复合材料蜂窝夹层结构翼梁优化设计［J］.机械制造研究，2009，38（3）：3-5.

［18］韩刘，齐辉，门坤发，等.基于界面单元的蜂窝夹层结构失效分析及验证［J］.哈尔滨工程大学学报，2022，43（6）：787-793.

责任编校：裴媛慧，陈 强

Analyses of Mechanical Properties of Honeycomb Sandwich Leading Edge of Wing Structures

ZHAO Hui1，WU Xiaoqiang2

（1. School of Aircraft Engineering， Xi’an Aeronautical University， Xi’an 710077， China;

2. School of Aeronautics， Northwestern Polytechnical University， Xi’an 710072，China）

Abstract：The mechanical properties of the whole honeycomb sandwich structure under the uniform aerodynamic loads of leading edge of the wing are studied in this paper.Firstly，the equivalent elastic parameters of the core layer of honeycomb sandwich structure are given，and the discrete honeycomb core in the structure is transformed into a homogeneous three-dimensional orthogonal anisotropic material according to the principle of mechanical equivalence by using the modified Gibson model.Then The bonding interfaces between the honeycomb core and the panels are modeled by the cohesive elements，and the carbon fiber reinforced composite panels are modeled with shell elements.Finally，the mechanical properties of the whole honeycomb sandwich structure are analyzed by using finite element method，showing the delamination process between the honeycomb core and the composite panel and the failure modes of the leading edge structure of the wing are obtained.

Key words：honeycomb sandwich；equivalent elastic constant；failure mode；finite element method；cohesive element

收稿日期：2024-01-25

作者简介：赵 慧，山西忻州人，讲师，研究方向为飞机结构强度。