多场耦合作用下凸轮轴摆动磨削工艺对残余应力影响规律分析

摘" 要： 为探讨摆动磨削工艺下，不同工艺参数对残余应力的影响规律，基于ABAQUS子程序DLOAD与DFLUX模拟磨削中的磨削热与磨削力进行热-力多耦合，建立多场耦合作用下凸轮轴摆动磨削残余应力场有限元模型，研究不同工艺参数对残余应力的影响，并通过XRD进行试验验证.结果表明，建立的有限元模型与试验误差少于16%，模型合理、可靠；摆动磨削能产生更大的残余压应力；增大摆动与幅度可以起到辅助加工的作用.研究结果为凸轮轴摆动磨削工艺提供了优化途径.

关键词： 凸轮轴；摆动磨削；热力耦合；残余应力

中图分类号：TG580""" 文献标志码：A""""" 文章编号：1673-4807（2024）01-062-06

DOI：10.20061/j.issn.1673-4807.2024.01.010

收稿日期： 2022-04-13""" 修回日期： 2021-04-29

基金项目： 中国博士后科学基金面上项目（2023M730939）

作者简介： 陈建志（1992—），男，博士，讲师，研究方向为先进结构钢表面完整性与疲劳性能.E-mail：jzchen@just.edu.cn

引文格式： 陈建志，柏小祥，李国超，等.多场耦合作用下凸轮轴摆动磨削工艺对残余应力影响规律分析［J］.江苏科技大学学报（自然科学版），2024，38（1）：62-67.DOI：10.20061/j.issn.1673-4807.2024.01.010.

Influence of camshaft swing grinding process on residualstress under multi-field coupling

CHEN Jianzhi， BAI Xiaoxiang， LI Guochao， GUAN Xiaoyan， WANG Yan， ZHOU Honggen

（School of Mechanical Engineering， Jiangsu University of Science and Technology， Zhenjiang 212100，China）

Abstract：In order to investigate the influence of different process parameters on residual stress in swing grinding process， the influence of different process parameters on the residual stress is discussed by developing ABAQUS subroutine DFLUX and DLOAD to simulate grinding heat and grinding force in the thermal-mechanical coupling， the finite element model of camshaft swing grinding residual stress field under the action of multi-field coupling was established， the influence of different process parameters on the residual stress is discussed， and the experimental verification is carried out by XRD. The results show that the error of the finite element model is less than 16 %， and the model is reliable. Swing grinding can produce larger compressive residual stress. Increasing the swing and amplitude can play an auxiliary role in machining. This study provides a way to optimize the camshaft swing grinding process.

Key words：camshaft， swing grinding， thermal mechanical coupling， residual stress

摆动磨削作为一种精密的磨削技术，在凸轮轴磨削过程中体现了较强的优越性.残余应力是评估工件表面完整性的最重要的因素之一，不合理的残余应力分布会影响工件的疲劳寿命、耐蚀性和可靠性［1］.因此，对于可控应力磨削工艺进行研究具有十分重要的意义［2-3］.

目前，磨削工艺参数对残余应力的影响研究较多.文献［4］利用回归分析方法得出了磨削表面残余应力与磨削因素的关系式，得出砂轮速度和磨削深度增大，磨削残余应力及应力层深度均增大；进给速度对磨削残余应力的影响较小，且随进给速度增大，磨削残余应力及应力深度均较小.文献［5］基于热力顺序耦合方法建立工件平面磨削残余应力场的有限元模型，分别对磨削深度、砂轮线速度及进给速度因素对工件表层残余应力研究，结果表明：在磨削过程中，工件表层同时存在着残余拉应力和残余压应力，与其他磨削参数相比，磨削深度对残余应力的影响最为显著.文献［6］研究了不同磨削工艺参数下螺旋伞齿轮残余应力分布规律，研究结果表明：齿轮凸面平行磨削方向残余压应力最小，磨削过程使齿面产生拉应力而亚表层产生压应力，热力耦合有限元仿真法能有效用于螺旋伞齿轮磨削残余应力的预测和分析.文献［7］提出了一种基于随机分布晶粒的磨削残余应力热力耦合残余应力建模方法，并通过试验验证耦合模型能准确的预测温度和残余应力上的多物理场.

但关于凸轮轴摆动磨削工艺对残余应力影响规律研究却鲜有研究，特别是摆动幅度、摆动频率、砂轮直径、砂轮宽度对磨削残余应力影响研究几乎没有.为此，文中基于ABAQUS/Standard通过编写DFLUX与DLOAD子程序模拟磨削中的磨削热与磨削力进行多场耦合作用下有限元模型的建立，探讨凸轮轴摆动磨削工艺参数对残余应力的影响规律，并通过X射线衍射法测得加工后凸轮轴残余应力进行试验验证.

1" 凸轮轴摆动磨削工艺分析

随着柴油机凸轮设计宽度的不断增加，加工难度不断加大，加工过程中残余应力超差风险增大，传统的切入法磨削不再适用.摆动磨削是指在磨削过程中砂轮除了与C轴联动沿X轴做直线运动外，还可以通过程序设置，沿Z轴做直线往复运动（图1）其摆动可用f（t）=Fsin（2πft）表示.通过摆动磨削可消除砂轮修整型面对凸轮型面磨削精度的影响，延长零件使用寿命.

凸轮轴在摆动磨削加工过程中，凸轮型面是一种曲率时刻变化的非圆轮廓，因此在顶圆处（D）、过渡区（G1、G2）、基圆处（J）磨削深度是一个逐渐增加的过程.使用VK-X1000共聚焦激光显微镜测量磨削后的凸轮轴表面形貌，测得磨削深度在D处为磨削深度变化范围为0～26.569 μm，在G1处磨削深度变化范围为0～9.837 μm，在J处磨削深度变化范围为0～61.081 μm，在G2处磨削深度变化范围为0～28.844 μm.

2" 有限元建模

2.1" 几何模型的建立及网格划分

凸轮型面在磨削过程中，在D、G1、G2、J处磨削深度是一个逐渐增加的过程，因此，将凸轮型面进行简化，以一个具有一定倾斜角度的平面磨削来模拟凸轮型面的磨削过程，为保证较高的计算精度，靠近磨削面划分较细的网格（0.003 mm），远离磨削面的划分.

2.2" 材料参数设置

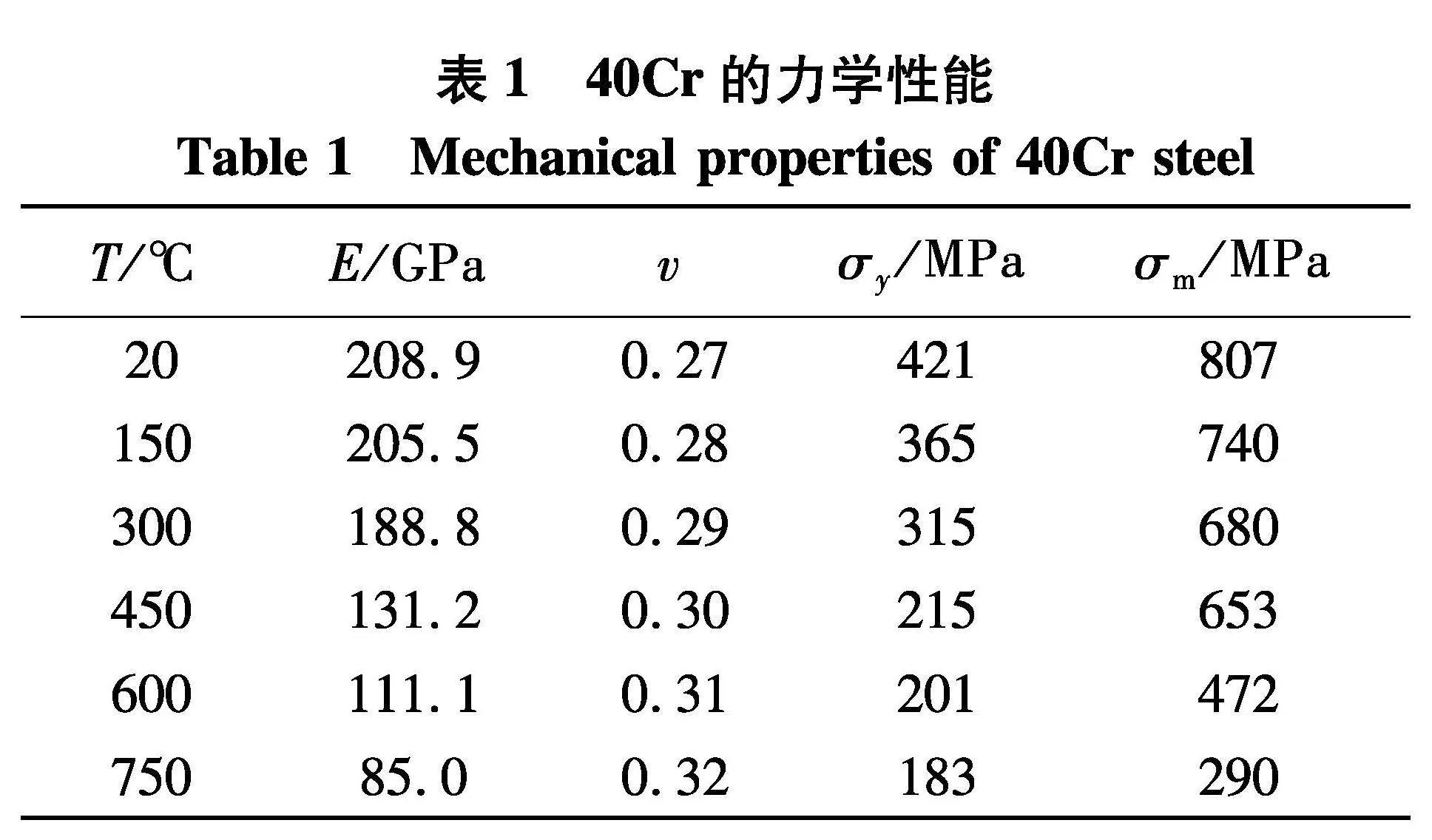
为了使仿真与实验结果具有可比性，模拟工件应与实验材料（40Cr钢）相同，弹性模量（E）、泊松比（v）、屈服强度（σy）、抗拉强度（σm）如表1，其导热率、热膨胀系数和比热取自文献［8］.

2.3" 温度场有限元模型的建立

在凸轮型面磨削加工过程中，工件材料的去除会消耗大量的热量并积聚在磨削区；与工件接触并发生切削行为的砂轮相当于一个移动热源，随着工件的进给，热源也在不断的向前移动.为分析磨削过程中产生的磨削热，需建立热源模型来将工艺参数与产生的磨削热联系起来［9］，热源模型的选择与仿真的精度密切相关，不同的热源模型，其仿真精度不同［10］.考虑到热源的接触来源；假设接触区域的摩擦系数是均匀的，则理论上压力和相应的热流分布应根据滑动/滚动接触方式建模.由于砂轮与凸轮型面的压力分布是呈椭圆形的，采用椭圆形的热源模型是合理的，热源的长度等于砂轮与工件之间的接触长度（2a=lc）.因此，进入工件的热流分布为：

qx=2Qπa" （1-x2a2）（1）

式中：Q为总热量（W/m）

在ABAQUS@/Standard中，移动热源通过FORTRAN子程序DFLUX集成到有限元模型中，热源沿水平（X+）轴移动.

磨削区产生的总热流密度包括流入工件的热流密度、流向砂轮的热流密度、流向磨屑的热流密度以及进入磨削液的热流密度［10］，与磨削区热量分配模型对应的方程为［11］：

qt=Ft·vsS=Ft·vsb" ap·D=qw+qch+qf+qs（2）

式中：qt为磨削区产生的总热流密度；S为工件与砂轮的接触面积；b为砂轮宽度；ap为磨削深度；D为砂轮直径；qw为流入工件的热流密度；qch为流向磨屑的热流密度；qf为进入磨削液的热流密度；qs为流向砂轮的热流密度.

2.4" 应力场有限元模型的建立

采用顺序耦合法，首先分析温度场，然后改变分析类型，将温度场的分析结果与外加力载荷耦合计算.其中外加力载荷由经验公式计算为［12-13］：

Fn=Fncut+Fnplow+Fnrub

Ft=Ftcut+Ftplow+Ftrub（3）

式中：Fn为法向磨削力；Ft为切向磨削力；Fncut为法向切削形成力；Ftcut为切向切削形成力；Fnrub为法向摩擦力；Ftrub为切向摩擦力；Fnplow为法向滑动力；Ftplow为切向滑动力.

将磨削力编写为ABAQUS的DLOAD子程序，其运动方式、摆动幅度、摆动频率、进给速度等参数均与热载荷DFLUX相同.具体多场耦合步骤如下：

步骤1" 复制工件模型，保持初始的材料属性.采用Static General替代Heat transfer分析步，将DC3D8单元转变为C3D8R单元类型.

步骤2" 对工件施加获取的磨削温度预定场，按每一增量步读取磨削温度场结果.

步骤3" 施加磨削力、约束条件等边界条件.

步骤4" 耦合磨削热、磨削力进行多场耦合计算，分析计算结果.

3" 试验验证

为验证建立有限元模型的合理性，采用X射线衍射法测量摆动磨削加工后凸轮型面的残余应力及其分布.

3.1" 凸轮型面残余应力测量

凸轮轴工件在完成外轮廓磨削加工并自然冷却后，为保证实验数据的准确性，分别在D、G1、J、G2处切割尺寸为3 mm×5 mm×2 mm且具有一定倾斜角度的方块，忽略线切割对残余应力的影响；检测每一块试样表面的残余应力，并对比测得的每个样件结果.实验采用加拿大Proto公司的高功率X射线残余应力分析仪进行试样检测.选用与凸轮轴相同材料的40Cr钢靶材，布拉格角为156.1°，采用侧倾法，扫描方式为固定φ角法，φ角分别取0、11.8°、-11.8°、17.48°、-17.48°、25°和-25°.

测量时，先用无水乙醇对试样表面进行清洗，然后吹干测量.每个凸轮型面分别检测线切割下来的4个块，每个块选取中间的3个点进行测量.

共检测12个点获得其沿凸轮型面轴向残余应力分布.每个检测点获得X、Y两个方向的残余应力，取3个点的平均值作为该处的残余应力值.

3.2" 仿真模型的验证

为验证仿真模型的合理性，随机选取如下加工工艺参数（表2）的工件进行测量.在仿真模型表面随机选取10个点，采用TRIMMEAN函数计算残余应力值.工艺1、2、3的实验值与仿真值对比如图2～4.结果表明：实验值与仿真值X方向上最大误差为15.6%，最小误差为2.32%，平均误差为4.94%；Y方向上最大误差为13.26%，最小误差为0.13%，平均误差为9.85%，仿真模型比较合理、可靠.在X方向上残余应力值分布为G2gt;Dgt;G1gt;J，在Y方向上残余应力值分布最大处为D，其余地方的分布不明显.

4" 结果与讨论

采用固定磨削深度ap=0.002 mm、固定砂轮线速度vs=65 m/s以及固定的工件转速n=2 200 mm/min，探讨砂轮直径D、砂轮宽度B、摆动频率f、摆动幅度F这4个因素对凸轮型面G2处摆动磨削表面残余应力的影响，采用单因素法（表3）设计仿真模拟方案.

图5为F=2 mm，f=120 次/min，D=125 mm，B=15 mm仿真模拟云图.仿真结果如图6～9.

由图6～9可知，不同工艺参数下X方向残余应力与Y方向残余应力表面与沿深度方向变化规律具有一致性.由图6可知，X方向上与Y方向上摆动磨削产生的残余应力比不摆动磨削要大；残余应力随摆动幅度的增加先增加然后趋于平缓.沿深度方向当表面残余应力较大时，其趋于0的斜率更大.由图7、8可知摆动频率、砂轮宽度对表面残余应力的影响以及沿深度方向残余应力分布情况与摆动幅度的影响大致相当，但砂轮宽度的影响比摆动幅度与摆动频率更大.由图9可知，当砂轮直径增加时表面残余应力逐渐减小，沿深度方向，随着砂轮直径的增加，残余应力减小的越平缓.

对于上述现象可解释为：随着砂轮宽度的增加，加工区域增加，磨削力增大，有更多的磨削热产生，从而导致残余应力增加；当砂轮宽度增加到一定时，其加工区域不再增加［14］.增大摆动幅度与摆动频率亦可增大加工区域，然而增加的区域也是有区间的.增加砂轮直径，接触弧长增加从而导致磨削力减小，残余应力减小［15］.在磨削深度、砂轮线速度、工件转速相同的情况下，砂轮直径、砂轮宽度、摆动频率与摆动幅度对凸轮轴摆动磨削残余应力的影响中，砂轮直径的影响最显著，其次是摆动频率、摆动幅度，影响最小的是砂轮宽度.在实际加工中，应选择合适的加工参数，才能使得加工结束后，凸轮轴残余应力值在一个合理的范围内，从而使得加工质量更好.

5" 结论

基于ABAQUS用户子程序DFLUX和DLOAD模拟磨削中的磨削热与磨削力进行多场耦合作用下摆动磨削残余应力有限元模型，并进行XRD试验测量加工后凸轮轴残余应力验证有限元模型，得出以下结论：

（1） 摆动磨削残余应力的有限元分析是合理可靠.试验值与模拟值在X方向的最大误差为15.6%，平均误差为4.94%.在Y方向，最大误差为13.26%，平均误差为9.85%.

（2） 摆动磨削比普通切入法磨削具有更好的加工性能.在相同条件下，摆动磨削产生的残余压应力比普通切入法磨削产生的残余压应力至少增加20.9%，这是由于摆动磨削增加了散热面积和磨削力导致的.

（3） 在磨削深度、工件速度和砂轮线速度相同的情况下，通过增大砂轮的摆动幅度与摆动频率能增加磨削后工件的残余压应力，从而获得更好的磨削性能.

参考文献（References）

［1］" ZUBAIROVA L K， SVIRSHCHEV V I. Residual stress in grinding［J］. Journal of Materials Processing Technology，2014，34（9）： 603-605.

［2］" ZHANG H， LIU J， ZUO X. Numerical study of the effects of residual stress on fretting fatigue using XFEM［J］. Materials，2015，8（10）： 7094-7105.

［3］" AMM U， ALESSANDRA C， AKIHIKO K， et al. Elucidating grinding mechanism by theoretical and experimental investigations［J］. Materials， 2018， 11（2）：274.

［4］" 任敬心，孟庆国.磨削残余应力的有限元计算［J］.磨料磨具与磨削，1995（3）：31-35.

［5］" 李满宏，王克军，裴天河，等.基于ANSYS的磨削残余应力场仿真研究［J］.工具技术，2014，48（4）：32-36.

［6］" 梁志强，黄迪青，周天丰，等.螺旋伞齿轮磨削残余应力分布规律及仿真分析［J］.机械工程学报，2018，54（21）：183-190.

［7］" NIE Z G， WANG G， WANG L P， et al. A coupled thermomechanical modeling method for predicting grinding residual stress based on randomly distributed abrasive grains［J］. Journal of Manufacturing Science and Engineering，2019，141（8）： 1-12.

［8］" GUI J X， KANG K S， YI H， et al. Prediction and experimental research of abrasive belt grinding residual stress for titanium alloy based on analytical method［J］. The International Journal of Advanced Manufacturing Technology，2021， 115 （4）： 1111-1125.

［9］" LIU T， DENG Z H， LV L S， et al. Theoretical and experimental study of temperature field in noncircular high-speed grinding［J］. The International Journal of Advanced Manufacturing Technology，2020，107（8）： 3581-3592.

［10］" MARIUSZ D， LINUS L， ECKART U. Thermal and technological aspects of double face grinding of C45 carbon steel［J］. Journal of Manufacturing Processes，2021，64： 1036-1046.

［11］" 何玉辉，徐彦斌，唐进元，等. 磨削弧区高阶函数热源分布模型研究［J］.机械工程学报，2019，55（7）：199-206.

［12］" HUANG X， REN Y， ZHOU Z， et al. Experimental study on white layers in high-speed grinding of AISI52100 hardened steel［J］. Journal of Mechanical Science and Technology，2015，29（3）： 1257-1263.

［13］" TANG J Y， JIN D， CHEN Y P. Modeling and experimental study of grinding forces in surface grinding［J］. Journal of Materials Processing Technology，2009，209（6）： 2847-2854.

［14］" 李琛，张飞虎.稀土氧化物激光晶体超精密磨削机理及工艺研究［J］.机械工程学报，2021，57（24）：131-132.

［15］" 葛德亮，陈科钧，郭德琅，等.硬质合金材料磨削机理的仿真与实验研究［J］.冶金管理，2020（9）：22-23.

（责任编辑：曹莉）