培养小学生数学模型意识的实践与思考

［摘 要］模型意识是数学模型普适性的初步体验，是形成模型观念的经验基础。在教学中，引导学生学会用“数学的眼睛”观察生活、用“数学的思维”思考现象、用“数学的语言”表述本质，使学生的模型意识逐步从朦胧走向清晰，最终达到深刻的理解。

［关键词］数学模型；小学数学模型；模型意识

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）29-0094-03

《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）指出，在数与代数领域的学习过程中，应着重培养学生的模型意识。《课程标准》提出具体教学要求，即通过创设恰当的问题情境，引导学生分析情境中的数量关系，并能够用数学语言准确表述情境中的数量关系。笔者对苏教版四年级下册数学教材中的“常见的数量关系”进行了深入探索，并设计一节以“路程、时间与速度”为主题的建模课。该课程的教学流程分为三个阶段：提炼生活问题→建立速度模型→应用速度模型。在创设的情境中，学生能够逐步认识到速度、路程和时间三者的关系。

一、感性表述在情境中提炼

（一）从数据中提出数学问题

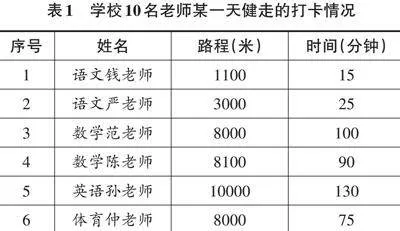
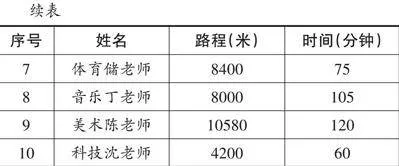
师：同学们，近期我们市将举行第九届全民“万步有约”健走激励大赛，学校将从报名的10名老师中选择1名老师参加这个活动。这是某天报名的老师的打卡数据（见表1）。学校想从报名的10名老师中选择1名老师参赛，如果你是评委，你会选择哪位老师，为什么？

（二）从讨论中提出比较快慢

生1：我会选择美术陈老师，因为他走的路程最远。

生2：我觉得可以根据花费时间的长短来选择，英语孙老师的运动时间最长，我会选择孙老师。

生3：我不同意他们俩的说法，我觉得哪位老师走得快就选择哪位老师。

生4：可是怎么样才能知道哪位老师走得最快呢？

师：从4名同学的发言中，我们听到了三种选择标准，一是选择路程远的，二是选择时间长的，三是选择走得快的。但是，走得快慢不太好比较。我们大家一起来看一看、想一想，有没有一眼就能比较出快慢的数据。

生5：我发现有三名老师的路程都是8000米，但是时间不一样，时间最短的是体育仲老师，只用了75分钟，所以这三名老师中体育仲老师是走得最快的。

生6：我们还可以看到体育仲老师和体育储老师用的时间都是75分钟，但是储老师走的路程更远，所以储老师走得比仲老师快。

师：这两名同学比较得有理有据，有谁能描述一下他们分别是怎么比较快慢的？

生7：如果所走的路程一样，就看所用的时间，用的时间长的走得慢，用的时间短的走得快；如果所用的时间一样，就看所走的路程，路程远的走得快，路程短的走得慢。

师：很棒！路程和时间都能够影响快慢。

生8：但是，这样比较还是有漏洞。

师：漏洞在哪儿呢？

生8：在前面的比较中，我们可以知道在数学范老师、音乐丁老师、体育仲老师和体育储老师四名老师中，体育储老师走得最快的。可是，体育储老师跟其他老师怎么比呢？

二、理性刻画在思考中发生

（一）定标准

时间不同、路程也不同，如何比较快慢？如何将时间或路程进行统一呢？教师可以引导学生定标准，寻找不同的策略。

师：我们来研究体育储老师和科学沈老师的速度，这两位老师所用的时间不同，所走的路程也不一样，谁走得更快呢？

（学生分组探究，然后集体交流）

师：哪个小组来汇报一下你们组的比较方法和结果？

生1：我们组先将两位老师的路程变成一样的，有两种方法。第一种：沈老师走4200米用了60分钟，如果按这个速度再走一个4200米，还需要60分钟，这样沈老师走8400米的话，就用了60+60＝120（分钟），而储老师走8400米只需要75分钟，储老师走得快些。第二种：将储老师的8400米看作是2个4200米，时间也要平均分成2份，这样储老师走4200米需要37.5分钟，储老师走4200米的时间比沈老师短，储老师走得快些。

生2：我们组跟他们组不一样，我们是想办法将两位老师的时间变成一样。储老师所用的时间除以5，所走的路程也跟着除以5，这样储老师15分钟走了1680米；沈老师所用的时间除以4，所走的路程也跟着除以4，这样沈老师15分钟走了1050米。所以，储老师走得快些。

生3：我们组比的是两位老师1分钟的路程，用储老师的路程8400米除以75，算出她1分钟走112米；用沈老师的路程除以60，算出沈老师1分钟走70米。所以，储老师走得快些。

师：刚才三个小组汇报了他们的方法，这三种方法有什么相同的地方和不同的地方呢？

生4：生2所在的小组和生3所在的小组都是用“时间相同比路程”的方法，生2的小组把时间统一成15分钟，在15分钟里谁走的路程多谁就快；生3的小组把时间都统一成1分钟，在1分钟的时间里谁走的路程多谁就快。

生5：生1的小组采用“路程相同比时间”的方法，第一种是把沈老师的路程扩大变成8400米，这样两位老师的路程都是8400米，此时谁用的时间少说明谁走得快；第二种方法是把储老师的路程缩短到和沈老师一样，此时，谁用的时间短说明谁走得快。

生6：不管是哪种方法，只要统一路程或者统一时间，都可以比较出快慢。

（二）调标准

师：通过上面的讨论，我们知道了只要统一路程或者时间中的任何一个量，都可以比较出快慢。如果在刚刚的比较中再增加语文钱老师一起比较，你会采用哪种方法比较谁走得最快，谁走得最慢呢？

生7：前面已经知道储老师走得比沈老师快了，我们组就先比较沈老师和语文钱老师的快慢，采用的是“时间相同比路程”的方法。将时间都变成60分钟，我们发现钱老师60分钟能走4400米，所以钱老师比沈老师走得快，说明沈老师走得最慢；然后再将储老师和钱老师进行比较，时间统一为15分钟，钱老师15分钟能走1100米，储老师15分钟能走1680米，说明储老师是走得最快的。

师：听出来了，他们组是两两统一时间比路程。

生8：我们组觉得两两比较麻烦，我们组分工合作，分别算出每位老师1分钟走的路程，这样很快比较出走得最快和最慢的。

……

师：我发现没有小组采用“路程一样比时间”的方法，这是为什么？

生9：我们组尝试过将路程变成一样去计算，但是太麻烦，中途放弃了这种方法。

师：数学思考让比较变得简单。如果要一起比较10名老师谁走得最快，你选择哪种方法？

生10：用“路程÷时间”算出1分钟走的路程，再比较快慢的方法最简洁、最快。

生11：我赞成。

（三）揭速度

师：刚才大家都觉得把时间统一为1分钟，比较1分钟走的路程的方法最简洁。在数学中，将“一个单位时间内所走的路程称为速度”（板书）。刚才大家都是采用比较速度的方法来比较出快慢的。小结一下，怎么求速度？

（根据学生的回答，板书：路程÷时间=速度）

师：也就是说，哪些因素可以影响速度？

生（齐）：路程和时间。

在本模块的三个环节中，学生经历了比较两人、三人、多人快慢的过程，充分感受到统一时间的必要性，并从60分钟、15分钟、1分钟的比较中再次感受到统一单位时间的简洁与快捷，从而理解了速度就是单位时间内的路程这一概念。在此基础上，学生抽象出速度的概念，并概括出影响速度的两个主要因素，同时明确了速度与路程、时间之间的相互关系。

三、模型价值在运用中拓展

速度作为描述“快慢”的概念，具有抽象性，教学中，理解速度单位是一大难点。只有通过适当的练习，增加学生对“数”和“量”的认识，才能深化他们对速度单位的理解，并让他们认识到统一速度单位的重要性。

（一）在解决问题中感受价值

师：用路程除以时间算出每一名老师的速度，这样，即使运动的路程不同、时间也不同，我们也很容易能比较出快慢。

（教师用公式计算出每个老师的速度，并按“速度”进行降序的排列，绘制成表，表略）

生1：我发现“路程÷时间=速度”这个公式是万能的，这个公式统一了单位时间，方便我们比较快慢，比“相同路程比时间”的方法简单多了。

（二）在丰富素材中理解速度

师：提到速度快，不得不提到200米短跑运动员谢震业。

（教师播放谢震业200米跑的视频，并板书“谢震业跑200米用时19.88秒”）

师：观看了谢震业跑200米的视频。你有什么感受？会计算他的速度吗？

（学生回答计算速度的方法，教师用计算器计算出谢震业跑200米的速度为1秒跑10.06米）

师：也就是说谢震业1秒大约跑10米，哪个同学来形容一下1秒跑10米的速度有多快。

生1：“滴答”一声，他能从我们教室前面黑板这儿跑到后面黑板还不止，因为我们教室前后长只有9米。

师：人们常用“像蜗牛一样慢”来形容一个人的速度慢，蜗牛的速度究竟有多慢，我们来看一组数据。

（课件出示：蜗牛爬10米大约要1小时）

师：这组数据中也有“10米”，谁能描述一下这个“10米”的意思？

生2：这个“10米”的意思是1小时爬10米，也就是3600秒爬了10米。

师：从生2回答中我听出了蜗牛确实速度慢，3600秒才爬10米，而谢震业1秒就能跑10米。我们不能简单粗暴地给他们的速度都写“10米”，而是要加上单位名称，这样才能准确地表述出速度的快与慢。（板书如图1）

综上所述，只有让学生经历用“数学的眼睛”观察生活，用“数学的思维”思考现象，用“数学的语言”表述本质的过程，才能逐步让学生的模型意识从模糊走向清晰直至深刻。

［ 参 考 文 献 ］

［1］ 付丽，边靖.基于真实情境建构数学模型：“路程、时间与速度”教学实践与思考[J].小学教学（数学），2024（3）：72-75.

［2］ 李国强.2022年版课标中“数量关系”主题的价值意蕴与教学策略[J].教学月刊小学版（数学），2024（4）：9-14.

［3］ 马云鹏.怎样理解“数量关系”学习主题[J].小学数学教育，2022（11）：11-13.

【本文系江苏省教育科学“十四五”规划课题“基于整体建构的小学数学建模教学研究”（课题批准号：C-b/2021/02/79）的阶段性研究成果。】

（责编 梁桂广）