煤系岩体三维裂隙网络随机生成研究与应用

摘 要：【目的】更加清晰且直观地展现煤系岩体结构面的空间分布特征。【方法】基于地质学统计方法对实际裂隙资料进行分析，得到裂隙位置与密度、直径及产状等概率分布函数，借助MATLAB编辑程序，并利用Monte-Carlo随机模拟算法生成满足一定分布函数的随机变量。在此基础上，以Baecher圆盘替代实际裂隙，得到较为精准的三维裂隙网络模型。【结果】该模型不仅高度还原了实际裂隙的形态特征，还精确地再现了裂隙之间的空间关系，包括裂隙的相互交叉、平行分布和聚集区域等。【结论】将三维裂隙网络随机生成技术运用于煤系岩体裂隙探查中，不仅是研究裂隙几何特征的一种重要手段，而且可为后续岩体渗透性及开采安全性评估提供技术支持。

关键词：煤系岩体；三维裂隙网络；Monte-Carlo算法

中图分类号：TK124 文献标志码：A 文章编号：1003-5168（2024）16-0106-05

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.16.021

Study and Application of Random Generation of Three-Dimensional Fracture Network in Coal Measure Rock Mass

ZHANG Yichen LU Haifeng

（Anhui University of Science& Technology， Huainan 232000，China）

Abstract：[Purposes] This paper aims to reflect the spatial distribution characteristics of coal measures rock mass structural plane more clearly and intuitively. [Methods] The probability distribution functions of fracture location， density， diameter and occurrence were obtained based on geological statistical analysis of actual fracture data， and random variables satisfying certain distribution functions were generated by MATLAB editing program and Monte-Carlo stochastic simulation algorithm， thus forming a three-dimensional fracture network model. On this basis， the accuracy of the model was tested by comparing the parameters of the simulated crack model with those of the measured crack model. [Findings] The model not only highly restores the morphological characteristics of the actual cracks， but also accurately reproduces the spatial relationship between the cracks， including the cross， parallel distribution and aggregation area of the cracks.[Conclusions] The application of 3D fracture network random generation technology in coal measure rock fracture exploration is not only an important means to study the geometric characteristics of fractures， but also provides technical support for the subsequent evaluation of rock permeability and mining safety.

Keywords： coal measure rock mass; three-dimensional fracture network; Monte-Carlo algorithm

0 引言

随着我国对煤炭资源需求的不断增长，开采深度也以每年8～10 m的速度增加。开采深度增加的同时，时常会因为岩土体裂隙过大或过多，导致岩体不稳，引发重大工程事故［1］。在实际开采过程中，岩体变形破坏和抗压强度大小均与裂隙面的强度和产状紧密相关。因此，分析煤系岩体工程问题时，岩体裂隙的空间分布特征是首要考虑的关键因素［2］。

由于岩体裂隙的成因十分复杂且分布具有随机性和多样性，直接进行测定非常困难。目前，只能通过少量的露头裂隙面及钻探等方式获取相关信息，但这些数据数量有限，且难以准确获取结构面的实际形态和大小。对此，三维裂隙网络随机生成技术为岩体内部裂隙结构面探索提供了一种可行途径。该技术可以高效、精准地模拟煤炭开采过程中岩体的裂隙空间分布特征，为煤炭开采提供技术支撑［3］。目前，国内外学者已对这一问题进行了深入研究，并取得了诸多成果。陈剑平［4］采用裂隙网络模拟技术及界面投影法获取了岩体关键位置；何忱等［5］利用等效列信息网络模型，构建了三维裂隙岩体渗流方法；王晋丽等［6］利用随机模拟技术生成了二维渗透裂隙网络；杜景灿等［7］通过蒙特卡罗算法确定了裂隙岩体的综合抗剪强度。

传统的二维裂隙模拟方法仅考虑平面展布，忽略了方位角度变化，与实际裂隙网络差异较大。三维地质随机模拟技术则更精确，能充分研究地质变量属性间的关系，确定裂隙变化趋势，为采矿设计等领域提供科学依据。本研究在已有数据的基础上，对淮南某一煤矿的岩体空间结构进行深入分析，结合Monte-Carlo算法与MATLAB编辑软件，并充分考虑裂隙产状和迹长，按照特定的分布规律建立三维裂隙网络。该方法不仅提高了煤矿开采的工作效率，还在极大程度上提升了开采过程的安全性，能够为后续各种工程实践开展提供数据支撑。

1 三维裂隙网络模拟原理

1.1 裂隙圆盘模型

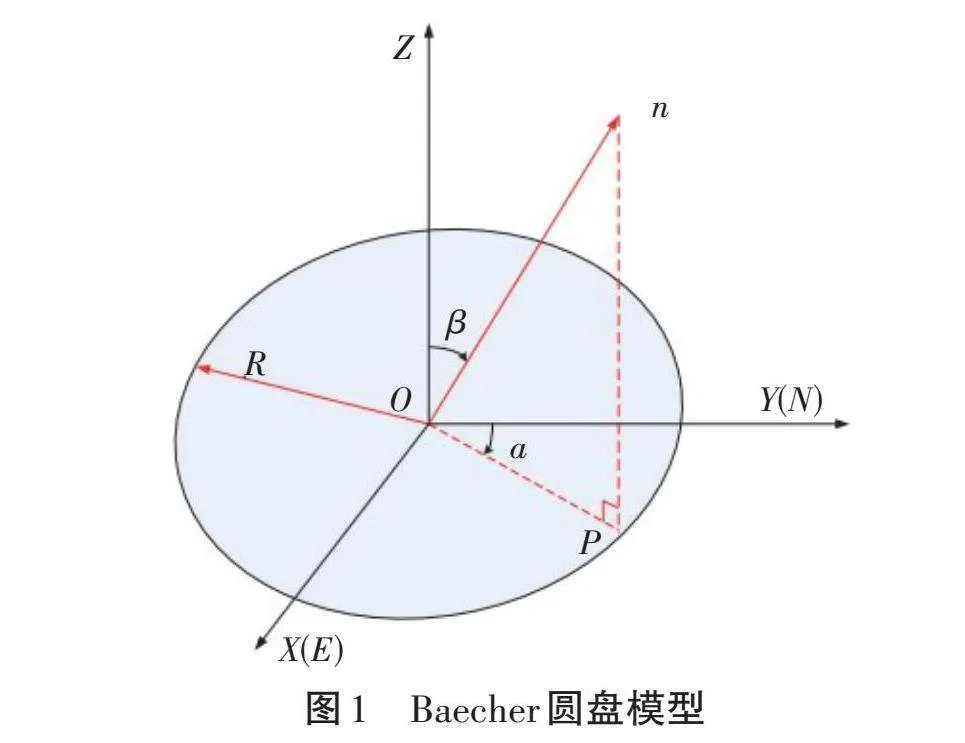
岩体裂隙形成于复杂的地质过程中，具有特殊的内部结构与复杂的分布规律。考虑实际裂隙形状未知，在建模过程中假定裂隙面为二维平面，采用Baecher［8］ 模型将裂隙简化为圆盘，以便于参数估计和数学建模。因此，每个三维裂隙圆盘均由圆心位置、产状（倾角、走向）唯一确定。Baecher 圆盘模型如图1所示。

圆盘裂隙可表示为式（1）。

[C=cO，V，R] （1）

式中：O为裂隙圆盘中心点坐标；V为裂隙产状（倾角与走向）；R为裂隙半径；其中[O=x0，y0，z0]，[V=α，β]，n为裂隙圆盘法向量，其关系式为式（2）。

[AX-x0+BY-y0+CZ-z0=0X-x02+Y-y02+Z-z02≤R2A=sinβsinαB=sinβcosαC=cosβ] （2）

其中：①裂隙圆盘倾角与走向相互独立且服从同一概率模型；②裂隙圆盘半径相互独立且具有相同分布类型；③裂隙圆盘的半径与产状互不影响。

1.2 煤系岩体三维裂隙网络模拟流程

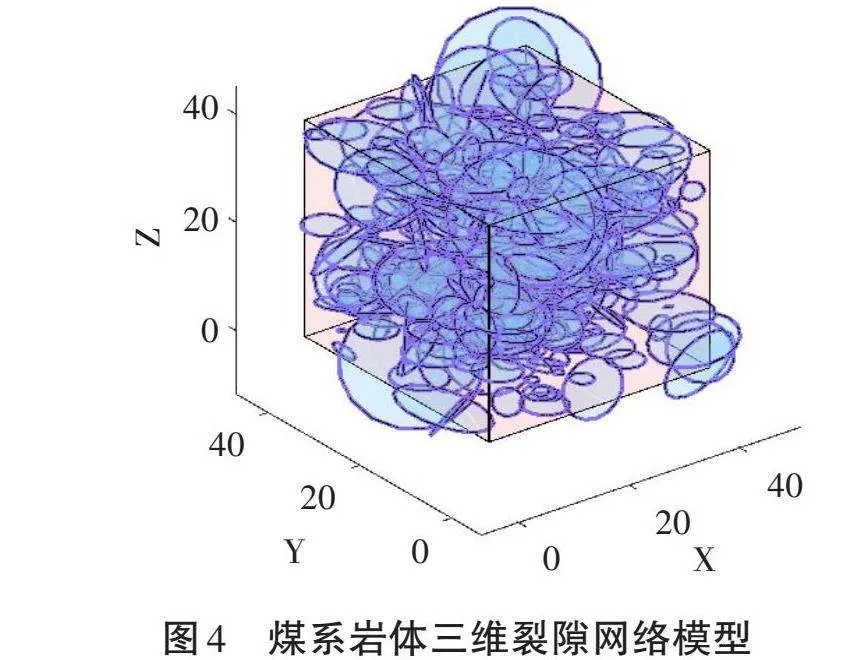
要建立Baecher圆盘模型，首先需要确定裂隙的半径、中心点坐标、倾角和走向等参数，本研究采用Monte-Carlo模拟产生裂隙参数。Monte-Carlo是以概率论为理论基础，通过一定的随机数生成方法，生成服从某一概率分布形式的随机数序列变量［9］。在实际工程项目中，煤系岩体裂隙分布随机且数量庞大，对其进行模拟具有一定的难度，但大量实践证明，裂隙的参数数据往往服从一定的概率分布。基于Monte-Carlo算法建立三维裂隙网络的过程是现场采样统计的逆过程：通过现场样本数据将裂隙进行分组，获取各个裂隙组参数均值、方差等数据，并建立相应的概率密度函数。在这些概率分布组合中随机组合圆盘圆心点、产状与直径大小构成三维裂隙网络模型，同时将模拟的裂隙网络与实际裂隙信息进行对比，验证其可靠性。具体流程如图2所示。

2 裂隙参数分析

2.1 裂隙位置及密度分析

煤系岩体的裂隙大多隐藏于地下，仅在煤炭开采过程中有少量裂隙露头，由于观测数据有限，很难精准掌握岩体裂隙的真实空间分布。根据数据统计经验，本研究假定圆盘裂隙中心点坐标遵循三维空间泊松点的过程。在模拟过程中每个裂隙被视为独立个体，裂隙中心点坐标[x0，y0，z0]服从均匀分布函数。此外，在构建裂隙圆盘中心点的泊松过程中，首先要确定裂隙结构面的空间密度特征。

在三维岩体裂隙随机模拟中，裂隙密度是重要的参数，它反映出一定研究区域内裂隙的发育程度，并控制着岩体的完整性。裂隙面发育程度越高、岩体强度越低、完整性越差，此时岩体渗透性较强。反之，则表明岩体强度较高、渗透系数较差。因此，在煤炭开采过程中常常会选择岩体发育程度较低的基岩，保障开采的安全性［10］。本研究以体密度的形式对煤系岩体三维裂隙密度进行计算，其计算公式为式（3）。

[Vρ=i=1nr3iV] （3）

式中：n为裂隙总数目；[ri]为裂隙平均迹长；[Vρ]为裂隙体密度系数；[V]为岩体体积。

通过对研究区域内每一个单元格裂隙中心点数据的计算，获取各个岩体单元中的裂隙密度，并根据Monte-Carlo算法模拟出三维裂隙片空间分布。Monte-Carlo随机模拟方法的基本原理是利用［0，1］区间标准均分随机数，根据已知裂隙几何参数的密度分布函数，求得的抽样公式来获得服从给定裂隙几何参数分布形式的随机变量。抽样公式主要包括：变换抽样法、复合抽样法和直接抽样法（又称反函数法），其中直接抽样法精准性较高、较为常用。具体思路方案为：假设随机变量[v]服从积累分布函数[Tv]和分布函数[tv]，则[Tv]的值域为［0，1］，[xi]为[Tvi]的函数值，其中[v]与[x]的对应关系为式（4）［11］。

[x=Tv=01tvdv] （4）

对式（4）进行变换，其反函数为式（5）。

[v=T-1x] （5）

将计算机随机产生的一系列均匀分布随机数[v1，v2，v3......vn]代入公式（5），即可得到随机变量V的模拟模型式（6）。

[Vi=T-1xi，i=1，2......n] （6）

式中：n为三维裂隙模拟次数，模拟的次数越多，结果越精准其分布频率越接近真实值。根据上述流程，计算出煤系岩体裂隙密度具有正态分布特征，在随机模拟出单位体积内的裂隙数目后，可得出裂隙圆盘的三维空间分布图

2.2 裂隙直径分析

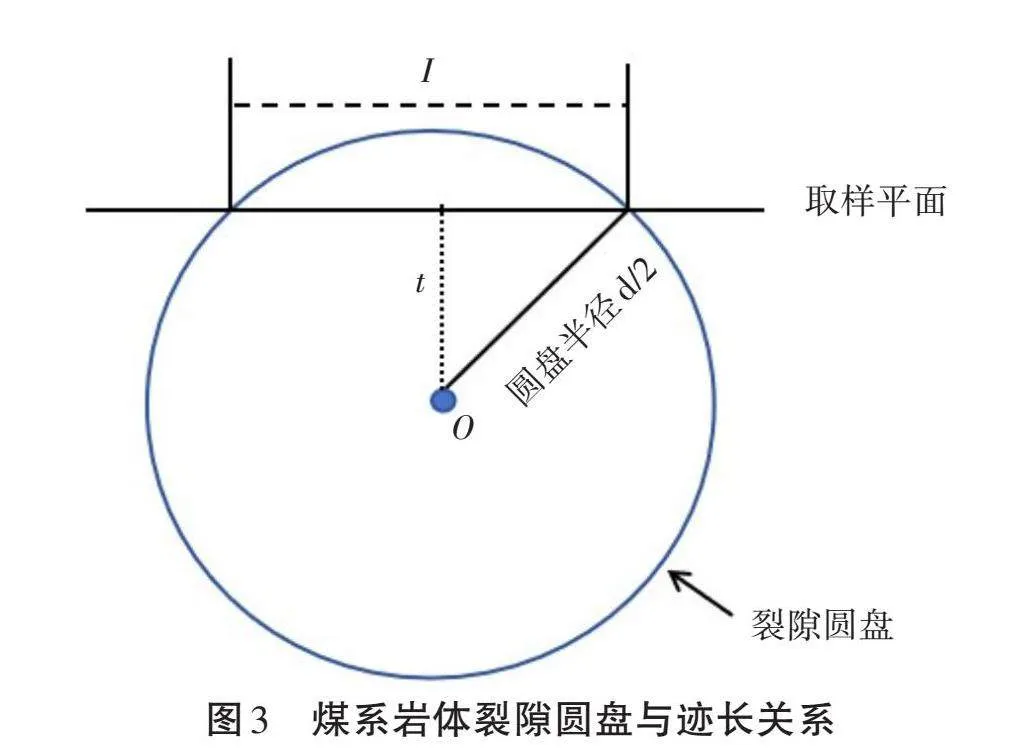
裂隙迹长是判断裂隙面大小的重要指标，但根据现有技术无法直接获取裂隙面的迹长。因此，若想确定圆盘裂隙的大小，首先要求出裂隙迹长与模拟圆盘之间存在的数学关系。在Baecher模型中将露头或开挖面上出露的裂隙迹长实际上就是裂隙圆盘的一条弦（如图3所示），且传统意义上认为真实裂隙迹长与模拟圆盘弦长具有相同的概率分布函数。模拟裂隙迹长的基本思路如下：假定模拟隙圆盘的直径遵循某一特定的函数分布规律。基于这一假设，利用式（7）直接推导出模拟裂隙迹长的拟合值，从而进一步确定裂隙迹长的分布几何特征［12］。这一过程不仅实现了对裂隙迹长与圆盘直径间复杂概率分布关系的有效简化，而且显著减少了传统方法中因误差校正而引入的复杂性与不确定性。

[t2+l22=d22] （7）

式中：裂隙圆盘半径为d/2；裂隙圆盘在取样平面迹长为l；迹长到圆盘圆心距离为t。

本研究采用对数正态分布函数形式表示裂隙迹长，对数正态分布函数的相关性质公式［13］见表1。

基于上述讨论，在假定三维裂隙圆盘直径服从对数正态分布函数的情况下，计算出统计窗内实际裂隙迹长相关参数，最终获取模拟裂隙圆盘直径的相关信息。

2.3 裂隙产状分析

在构建煤系岩体三维裂隙网络的过程中，一个关键特征是裂隙产状。它不仅对岩体裂隙空间方位状态及延展形态进行描述，而且对于裂隙优势组划分起着决定性作用。通常采用倾角与倾向两个变量来表征裂隙产状。在实际煤炭开采过程中，岩体中裂隙可能会呈现一个或几个聚集性优势组方向，每组裂隙平均产状计算时，由于坐标系不具有连续性，并不能直接将所有产状数据相加取其平均值。因此，在模拟不同产的裂隙时，裂隙结构面优势组划分及其函数分布形式也值得深入研究［14］。裂隙产状[V=α，β]通常服从均匀分布、对数分布、正态分布和对数正态分布等。

3 工程实例模型建立

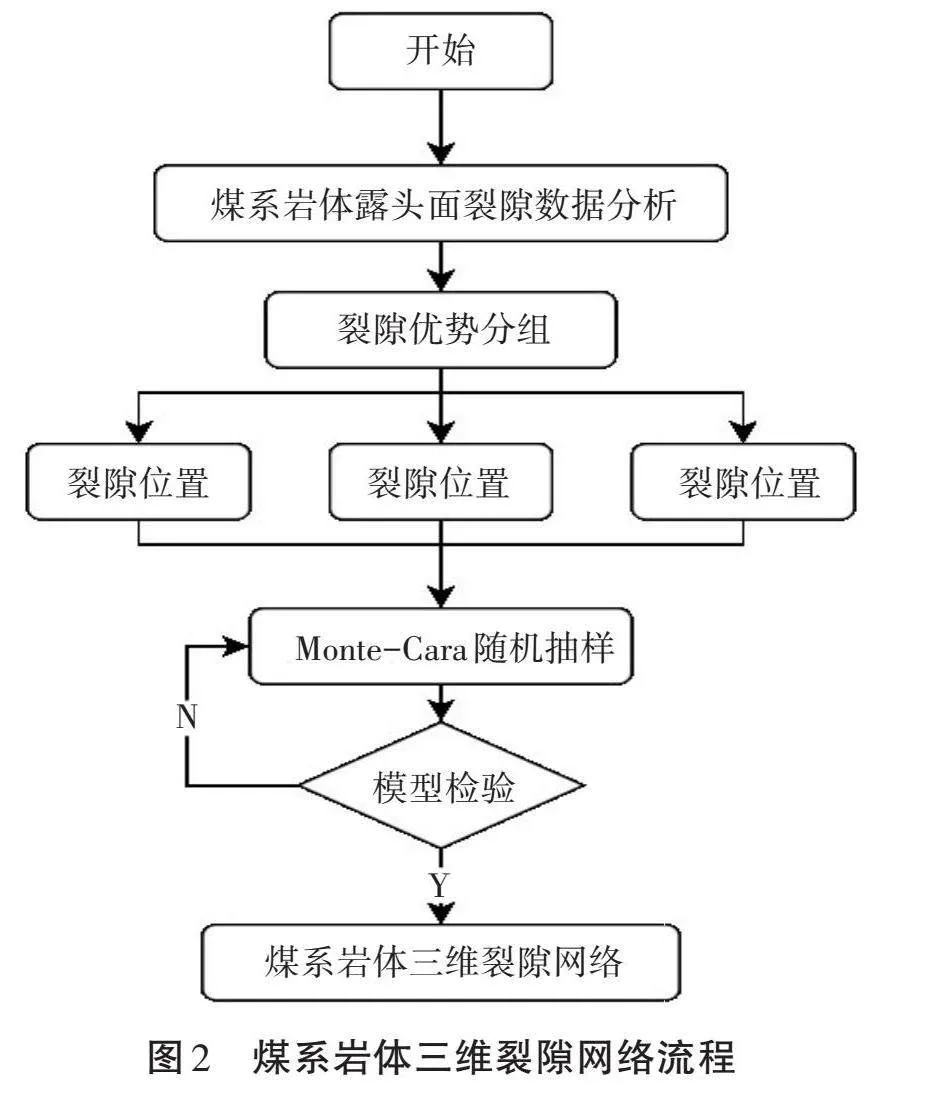
本研究以淮南某煤矿为例，对开采过程中露头面裂隙信息进行采样与统计分析，并建立各个参数的概率分布函数见表2。通过Monte-Carlo算法随机生成满足不同概率分布函数的岩体裂隙参数数据文件，结合MATLAB编辑程序生成三维裂隙图形（如图4所示），其中，模型尺寸为[X×Y×Z=40 m×40 m×40 m]。通过随机生成的三维裂隙网络模型，可以为开采人员提供较为直观的岩体裂隙图像资料，同时根据当前地质资料，可对煤炭开采过程中危险性和渗透性进行评估，为裂隙渗流计算和顶底板采动破坏提供较为准确的三维网络模型。

对模拟生成三维裂隙网络的各个参数进行统计，结果见表3。由表3可以看出，MATLAB程序生成的三维裂隙网络参数与实际较为接近，准确度较高，具有一定的实用性。

4 结论

本研究首先对三维裂隙网络随机生成的基本原理进行总结概括，了解三维裂隙网络生成的具体流程。其次对裂隙迹长、产状及空间位置概率分布进行分析，并采用Baecher圆盘模拟替代实际裂隙，根据淮南某煤矿具体数据完成三维裂隙网络模型的建立。利用Monte-Carlo算法，并结合露头面裂隙的统计数据，对煤系岩体中的裂隙网络进行三维随机模拟，不仅为岩体裂隙结构面的建模提供了一种较好的思路，而且对于后续岩体强度岩石质量指标评估及渗透性计算提供了技术支持。

参考文献：

［1］尹光志，李星，鲁俊，等.深部开采动静载荷作用下复合动力灾害致灾机理研究［J］.煤炭学报，2017，42（9）：2316-2326.

［2］张亚，彭乐文.基于Monte-Carlo的岩体三维裂隙网络模型研究［J］.甘肃科学学报，2020，32（2）：124-131.

［3］沈瑞文.裂隙网络的三维随机模拟方法研究［J］.黑龙江工程学院学报，2020，34（5）：11-16.

［4］陈剑平， 卢波， 谷宪民， 等. 用投影法求算岩体裂隙面三维连通率［J］. 岩石力学与工程学报. 2005（15）： 2617-2621.

［5］何忱， 姚池， 杨建华， 等. 基于等效离散裂隙网络的三维裂隙岩体渗流模型［J］. 岩石力学与工程学报. 2019， 38（S1）： 2748-2759.

［6］王晋丽，陈喜，张志才，等.基于离散裂隙网络模型的裂隙水渗流计算［J］.中国岩溶，2016，35（4）：363-371.

［7］杜景灿， 陈祖煜， 弥宏亮， 等. 三维条件下应用遗传算法与 Monte-Carlo 法确定节理岩体的综合抗剪强度［J］. 岩石力学与工程学报. 2004（13）： 2157-2163.

［8］BAECHER G B. Statistical analysis of rock mass fracturing［J］. Journal of the International Association for Mathematical Geology， 1983， 15（2）： 329-348.

［9］GUO L ， HU X ， WU L ，et al.Simulation of fluid flow in fractured rocks based on the discrete fracture network model optimized by measured information［J］.International Journal of Geomechanics，2018，18（10）：05018008.1-05018008.26.

［10］韩帅，李明超，王刚.基于控制圆法和迭代反演的岩体多边形裂隙网络模拟方法［J］.岩石力学与工程学报，2019，38（8）：1635-1646.

［11］魏亚强，董艳辉，周鹏鹏，等.基于离散裂隙网络模型的核素粒子迁移数值模拟研究［J］.水文地质工程地质，2017，44（1）：123-130，136.

［12］雷光伟.岩体节理几何特征研究及三维网络模拟［D］.重庆：重庆大学，2015.

［13］于青春，陈德基，薛果夫，等.裂隙岩体一般块体理论初步［J］.水文地质工程地质，2005（6）：42-48.

［14］ZHU Y，WANG X，DENG S，et al.Grouting process simulation based on 3d fracture network considering fluid-structure interaction［J］.Applied Sciences，2019，9（4）：667.