基于相对安全率的新型挡土墙安全系数标定

摘 要：【目的】为解决挡土墙设计中安全系数存在无法考虑土体参数不确定性影响的缺陷，进行新型挡土墙安全系数标定研究。【方法】通过结合相对安全率的定义和不确定分析方法，进行不确定性分析，得到可靠度指标相对安全率，并结合相对安全率的基本原理和新型挡土墙安全系数研究标定，最终得到新型挡土墙安全系数的标定值。【结果】结果表明，基于不确定性分析和相对安全率基本原理求得的抗倾稳定安全系数允许值为1.37，抗滑稳定安全系数允许值为1.39，与规范规定的安全系数标准值1.6存在一定差异。【结论】研究成果可为新型挡土墙安全系数标定提供思路。

关键词：新型挡土墙；抗倾稳定安全系数；相对安全率；安全系数标定

中图分类号：TU476 文献标志码：A 文章编号：1003-5168（2024）16-0072-04

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.16.014

Calibration of Safety Coefficient for New Type Retaining Wall Based on Ratio of Safety Margin

TU Yaocheng ZHANG Han

（Chongqing Water Conservancy and Electric Power Construction Survey，Design and Research Institute Co.， Ltd.， Chongqing 404100，China;

2.Zhongshui North Survey Design and Research Co.， Ltd.， Tianjin 300000，China）

Abstract： [Purposes] To solve the defect that the safety factor cannot consider the influence of soil parameter uncertainty in the design of retaining wall， the calibration of safety factor of new retaining wall is studied. [Methods] By combining the definition of ratio of safety margin with uncertainty analysis methods， uncertainty analysis is made to get the reliability ratio of safety margin. Utilizing the basic principles of safety coefficient， the safety factor for the novel retaining wall is calibrated， ultimately obtaining the calibrated value. [Findings] The results show that the ratio of safety margin for overturning stability and sliding stability， derived from uncertainty analysis and the basic principles of ratio of safety margin， are 1.37 and 1.39， respectively. These values exhibit certain discrepancies with the specified safety factor standard value of 1.6. [Conclusions] The analytical results presented herein can offer insights into the calibration of safety factors for novel retaining walls.

Keywords： new type retaining wall; safety factor for overturning stability; ratio of safety margin; calibration of safety coefficient

0 引言

我国《水工挡土墙设计规范》（SL379—2007）为水利工程挡土墙设计提供了重要参考，给出了不同级别挡土墙的安全系数规范值，对于1～4级挡土墙安全系数允许值分别为1.35、1.30、1.25、1.20，可见对于不同等级的水工挡土墙，我国规范给出了不同的安全标准［1-2］。然而通过对，《加拿大地基手册》和美国公路局相关规范的查阅可知，不同国家的规范允许值存在较大差异，其中《加拿大地基手册》规定的允许值为1.5～2.0。因此，水工挡土墙岩土参数的固有不确定性为挡土墙稳定安全分析带来了挑战。由于规范的制定依赖于工程经验且存在一定的滞后性，如何拟定安全系数允许值，对工程设计至关重要。为了解决以上两个问题，考虑岩土参数不确定性对安全分析影响的可靠性分析方法，在水利工程和岩土工程中广泛应用［3］。陈祖煜等［4］基于可靠性分析结果和确定性计算指标（安全系数），建立了可靠度理论指导下的安全系数标定关系。提出相对安全率，并指出基于相对安全率的安全系数标定结果能够提供与可靠度相同的岩土结构安全富裕度。李典庆等［5］在此基础上建立了广义可靠指标相对安全率指标，实现了安全系数任意概率分布条件下的安全系数和可靠指标广义相对安全率的合理应用。可见，通过相对安全率对安全系数进行标定，可以进行规范之外的挡土墙安全系数允许值判定，是对现有挡土墙设计规范的有效补充。新型挡土墙的出现，很大程度上解决了传统挡土墙在施工周期和经济环保上的弊端。然而，对这类新型挡土墙的安全性的研究还相对较少，特别是现有规范允许值对其安全分析的适用情况还不清楚。因此，有必要对新型挡土墙安全系数标定进行研究。

鉴于此，本研究在相对安全率和可靠性设计基本理论的指导下，结合某一新型挡土墙工程，通过标定新型挡土墙的安全系数允许值，定量给出新型挡土墙确定性安全分析的安全富裕度，同时明确岩土参数不确定对新型挡土墙安全富裕度的影响，分析岩土参数变化对新型挡土墙安全的影响规律，为新型挡土墙的结构设计和安全评价提供依据。

1 相对安全率的定义

1.1 安全系数相对安全率

陈祖煜等［1-2］给出了不同概率分布条件下相对安全率的公式，当安全系数（FS）符合正态分布时，安全系数相对安全率[ηF]见式（1）。

[ηF=FSkFSa] （1）

式中：[FSk]为安全系数系数标准值，见式（2）；[FSa]为安全系数系数允许值。

[FSk=R（xk）S（xk）] （2）

式中：R为挡土墙的抗力；S为作用在挡土墙上的主动力；[xk]为确定性计算中参数的[xi]的标准值；k为参数的总数。

当FS符合对数正态分布时，[ηF]见式（3）。

[ηF=MkMa=lnFSk+1lnFSa+1] （3）

式中，[Mk]、[Ma]是中间变量；[FSk]为安全系数系数标准值；[FSa]为安全系数系数允许值。为便于分析通过中间变量M，将对数正态分布条件下的极限状态方程（M-1=0）转化为正态分布条件下的极限状态方程[FS-1=0]相同的形式。

分析式（1）和式（3）可知，当FS符合正态分布时，[ηF]>1保证了[FSk>FSa]，结构处于安全状态。另外由于对数函数是单调递增函数，当[ηF]>1，式（3）保证了[FSk>FSa]。因此在式（1）和式（3）中，通过不同的表达形式保证了一致的安全判据。

1.2 可靠度指标相对安全率

与安全系数相对安全率的定义过程类似，陈祖煜等［1-2］研究了可靠度指标相对安全率，从而实现确定性计算和不确定性计算之间的定量关系。针对正态分布和对数正态分布两种形式，给出了相对安全率的定义，正态分布可靠度指标相对安全率[ηR]见式（4），对数正态分布可靠度指标相对安全率[ηR]见式（5）。

[ηR=β-βaσFS+1] （4）

[ηR=β-βaσM+1] （5）

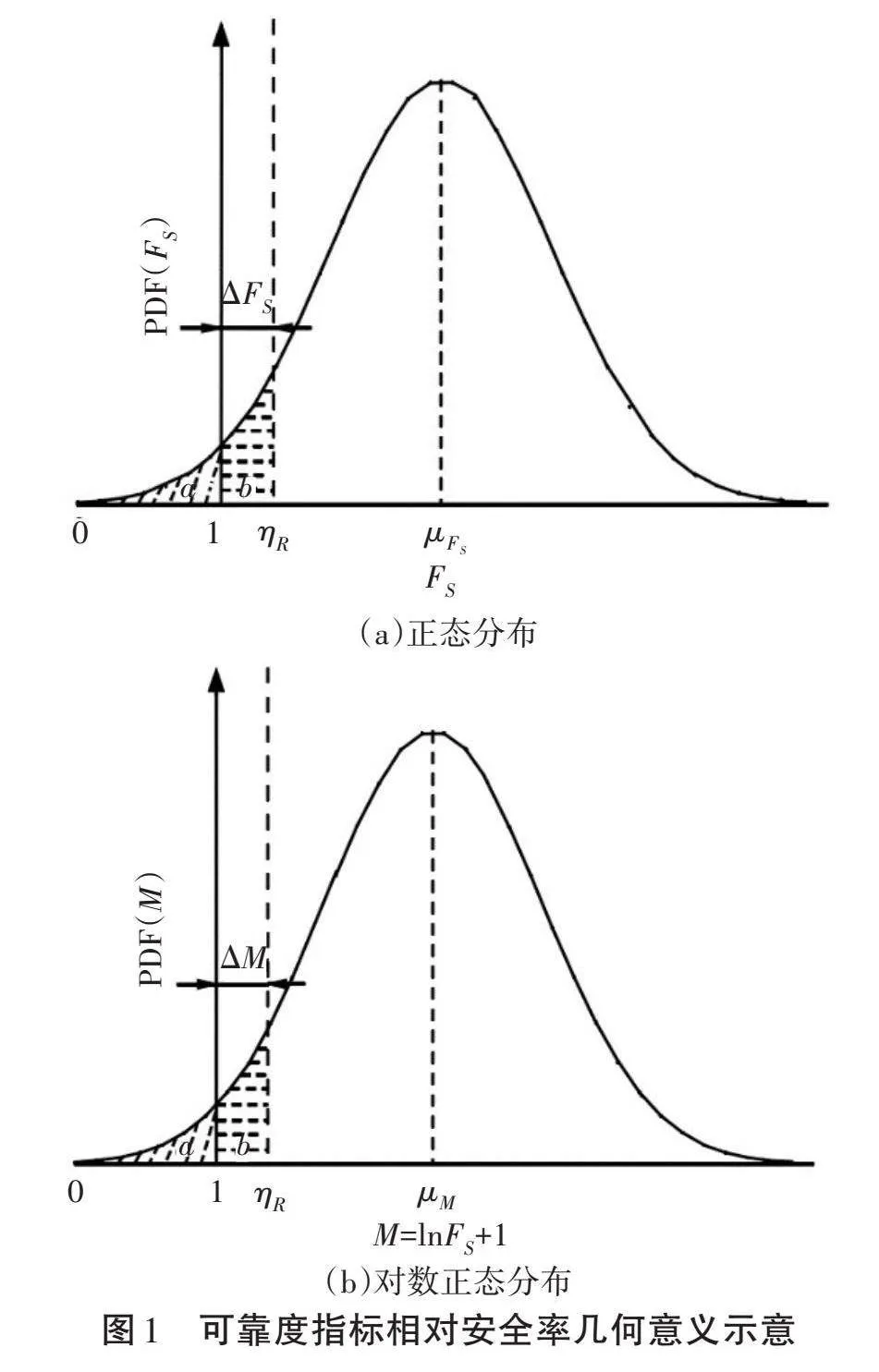
式（4）和式（5）中，[σ]为标准差。为便于理解，图1分别根据正态分布和对数正态分布的概率密度函数，对可靠度指标相对安全率[ηR]进行了进一步解释。在正态分布分布情况下，[FS=1]代表结构的失效边界，显然，[ΔFS=ηR-1]代表与结构失效边界的距离，即为结构的安全富余。类似在对数正态分布中，[ΔM=ηR-1]代表与结构失效边界的距离。从图1中可以看出，[ΔFS]和[ΔM]在结构安全富余度的表征上是一致的。

对于某一特性结构，存在一个规范规定的可靠性指标[βa]，当[ΔFS]或者[ΔM]为0时，即[ηR]=1，表明结构的可靠度富余为0。陈祖煜等［1-2］通过工程实例证明可靠度指标相对安全率[ηR]和安全系数相对安全率[ηF]在结构安全富裕度的表征上是等价的。也就是结构在两种相对安全率为[ηR=ηF]时，结构确定性设计和不确定性设计（可靠度设计）的富裕度相等，两种设计方式等效。因此，可以通过可靠度设计对确定性设计的安全系数进行标定，从而实现对安全系数的合理标定，对规范允许值进行补充。

2 新型挡土墙安全系数标定

2.1 案例分析

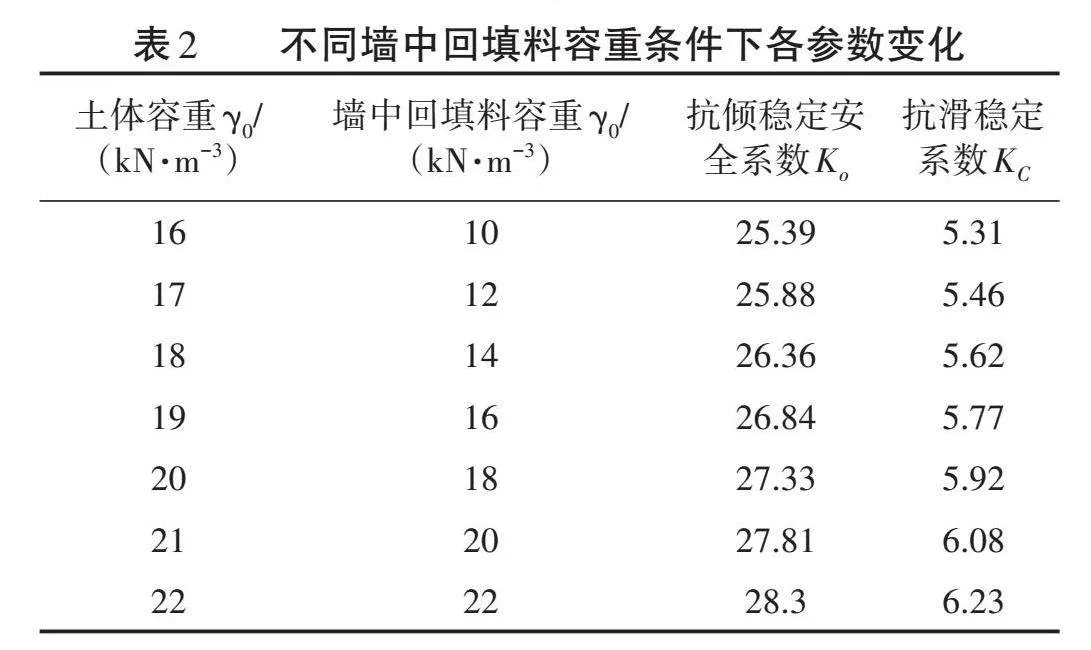
确定性计算是不确定计算的基础。本研究对该新型挡土墙进行抗滑稳定计算、墙体抗倾覆计算以及墙体基底压力验算。墙背土压力计算见式（6）、式（7），被动土压力计算公式见式（8）、式（9）。为便于分析，各参数见表1。

[Fa=12γH2Ka] （6）

[Fa=12γH2Kp] （7）

[Ka=cos2（φ-ε）cos2εcos（φ+δ）+[1+sin（φ+δ）（φ-β）cos（φ+δ）cos（ε-β）]2] （8）

[Kp=cos2（φ+ε）cos2εcos（φ-δ）+[1-sin（φ+δ）（φ+β）cos（ε-δ）cos（ε-β）]2] （9）

抗倾覆稳定和抗滑稳定安全系数是反映挡土墙稳定性的重要指标。本文以抗倾覆稳定和抗滑稳定为研究对象，分析挡土墙的稳定性，并计算相应的安全系数，计算公式可参考式（10）和式（11）。

[ηR=β-βaσFS+1] （10）

[ηR=β-βaσM+1] （11）

式中：[Ko]为抗倾稳定安全系数；[KC]为抗滑稳定安全系数。

2.2 不确定性分析

本文采用蒙特卡洛模拟执行不确性分析，建立基于灰狼优化算法（GWO）优化的支持向量（SVM）代理模型，用于替代蒙特抽样的计算过程［6］。GWO优化SVM流程如下：①初始化GWO，设置基本参数P、T和N，获得狼群初始位置；②初始化SVM，构造准确率为标注的适应度函数，设置超参数c、g搜索范围；③输入数据，计算当前适应度值，进行迭代计算，迭代次数≤N，获得最佳超参数c、g；④将GWO寻优获得的最佳超参数c、g带入SVM模型，即获得GWO优化的SVM最优模型。

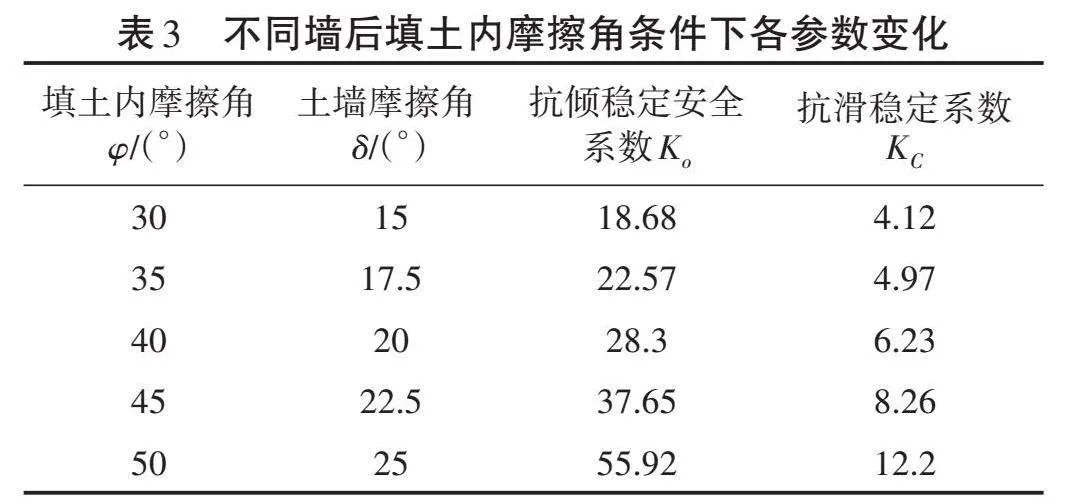
将表2、表3的基础数据作为GWO-SVM模型的训练数据进行训练。为了评价GWO-SVM模型的代理效果，选择4种模型性能指标用于衡量模型的综合表现，分别是均方根误差（RMSE），平均绝对误差（MAE），平均绝对百分比误差（MAPE），决定系数（R2）。以抗倾稳定安全系数预测结果为例，在测试集上GWO-SVM模型的R2为0.96，RMSE、MAE和MAPE均较小，代替模型精度较高，能够实现对确定性计算的替代，见式（12）至式（15）。

[MAE=1nni=1|yi-yi|] （12）

[RMSE=1nni=1yi-yi2] （13）

[MAPE=100nni=1|yi-yiyi|] （14）

[R=ni=1（yi-y）yi-yni=1yi-y2ni=1yi-y2] （15）

式中：n为测试样本中样本点个数；yi为测试集中第i个样本的实测值；[yi]为测试集中第i个样本的预测值；[y]为测试集预测值均值；[y]为测试集实测值的均值。

结合前人研究，确定本文涉及的土体参数的变异系数和分布形式，其中土体容重符合正态分布N～（18.9，1.55^2），变异系数为0.08；墙中回填料容重符合正态分布N～（15.71，3.05^2），变异系数为0.19；填土内摩擦角符合正态分布N～（40，7.07^2），变异系数为0.18；土墙摩擦角符合正态分布N～（20，3.54^2），变异系数为0.18。执行100 000次蒙特卡洛抽样，代入代理模型进行统计分析进而得到不确定分析结果可靠度指标，计算见式（16）。在本文中对抗倾稳定安全系数[Ko]和抗滑稳定系数[KC]对应的可靠性指标分别进行求解。求得抗滑稳定可靠性指标[β]为6.1，抗倾稳定可靠性指标[β]为7.5，远大于规范值一类破坏Ⅲ级规范值2.7。可见分析的新型挡土墙的安全富余还较大，因此对挡土墙安全系数允许值进行重新标定。

[β=μzσz] （16）

式中：[μz]为安全指标的期望；[σz]为安全指标的期望的方差。

3 新型挡土墙安全系数标定

通过和可靠度指标第2节计算得到的抗滑稳定可靠性指标[β]为6.1，抗倾稳定可靠性指标[β]为7.5。结合允许的规范值[βa]=2.7。根据式（4）求得相对安全率进行[ηR抗倾=1.61]，[ηR抗滑=1.76]。通过第1节分析指出，相对安全率[ηR=ηF]，结构确定性设计和不确定性设计（可靠度设计）的富裕度相等。根据蒙特卡洛计算结果，抗倾稳定[FSk]为2.21，抗滑稳定[FSk]为2.46。根据式（1）和[ηR=ηF]的前置条件，求得抗倾稳定[FSa]为1.37，抗滑稳定[FSa]为1.39。可见对于不同的安全指标（抗倾稳定和抗滑稳定系数），得到的安全系数允许值存在差异，但比较接近。另外，通过与规范规定的安全系数标准值1.6比较发现，规范值和标定的允许值存在一定的差异。研究表明，规范值未考虑材料参数不确定性对计算结果的重要影响，通过相对安全率来衡量挡土墙的安全富余更合理。

4 结论

①通过GWO-SVM替代确定性计算，能够获得较好的模拟精度，在测试集上GWO-SVM模型的R2为0.96，代理模型的高精度计算为不确定性分析和安全系数的标定提供了重要基础。

②通过对抗倾稳定和抗滑稳定安全系数进行标定，求得抗倾稳定的安全系数允许值为1.37，抗滑稳定安全系数稳定值为1.39，与规范规定的安全系数标准值1.6存在一定差异。

③通过不确定分析和抗倾稳定和抗滑稳定安全系数标定结果发现，该新型装配式挡土墙存在一定的安全富余，还有进一步优化设计空间。在设计挡土墙时，应该重视土体材料参数变异性对标定结果的影响。

参考文献：

［1］陈祖煜， 黎康平， 李旭， 等. 重力式挡土墙抗滑稳定容许安全系数取值标准初探［J］. 岩土力学， 2018， 39（1）： 1-10.

［2］陈祖煜. 建立在相对安全率准则基础上的岩土工程可靠度分析与安全判据［J］. 岩石力学与工程学报， 2018， 37（3）： 521-544.

［3］李典庆，唐小松，周创兵，等.基于Gaussian Copula函数的相关非正态岩土体参数不确定性分析［J］. 中国科学：技术科学，2012，42（12）：1440-1448.

［4］陈祖煜， 章吟秋， 宗露丹， 等. 加筋土边坡稳定分析安全判据和标准研究［J］. 中国公路学报， 2016， 29（9）： 1-12.

［5］李典庆， 周强， 曹子君. 基于广义可靠指标相对安全率的岩土工程设计安全判据［J］. 岩土力学， 2019， 40（10）： 3977-3986.

［6］王朝兵， 靳福涛， 张龙， 等. 基于ICEEMDAN与支持向量机的轴承故障诊断方法［J］. 机械设计与研究， 2023， 39（3）： 115-120.