隧道塌方风险评估研究

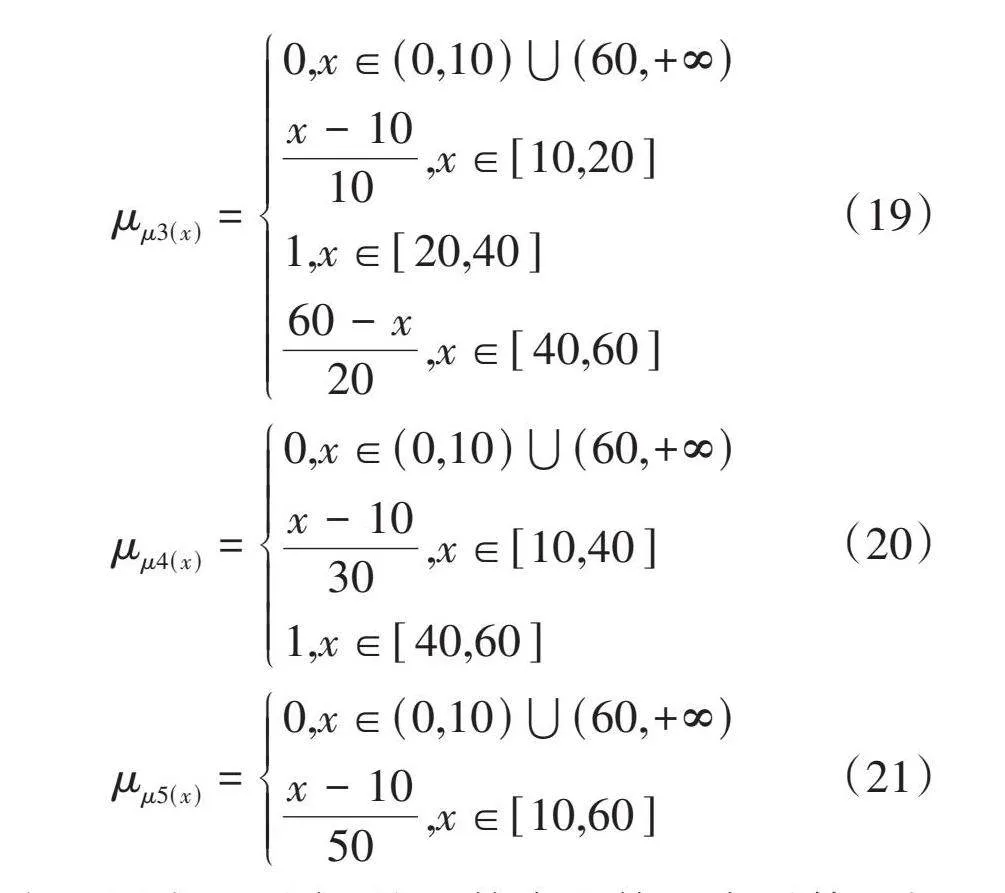
摘 要：【目的】随着“一带一路”倡议的推进，各类隧道不断建设，其间，工程事故也时有发生，其中尤以岩溶隧道塌方居多，为了确保隧道施工安全，进行岩溶隧道塌方风险评估尤为重要。【方法】针对模糊层次分析法定量分析不足的缺点，在计算权重值时引入Borda序值法，选取围岩级别、开挖跨度、埋深、地下水、施工技术与管理水平等5个指标，以优化后的模糊层次分析法建立了岩溶隧道塌方风险评估模型。【结果】以优化后的模糊层次分析法对某隧道塌方风险进行评估，判断其最终风险等级为Ⅲ级。【结论】通过引入Borda序值法，能有效降低模糊层次分析法的主观性，使用该模型评估的岩溶区隧道塌方风险等级与案例实际情况基本一致，说明该模型具有较好的实用性。

关键词：岩溶隧道；风险评估；模糊层次分析法；Borda序值法

中图分类号：U458.3 文献标志码：A 文章编号：1003-5168（2024）16-0058-08

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.16.012

Study on the Risk Assessment of Tunnel Collapse

—Application of Fuzzy Analytic Hierarchy Process（AHP） Optimization Model by Introducing Borda

Sequence Value Method

ZHANG Jun1，2 XIE Dingxi1，2 ZHANG Xin1，2 BAI Yongzhi3

（1.School of Civil Engineering， Changsha University of Science & Technology，Changsha 410114， China;

2.Key Laboratory of Bridge Engineering Safety Control by Department of Education， Changsha University of Science and Technology，Changsha 414000， China; 3.Xing'an League Jingwei HighwpGLGkj1kGwd+pDLy6W7AqA==ay Survey and Design Co.， Ltd.，Xing'an League 137400， China）

Abstract： [Purposes] With the implementation and advancement of the Belt and Road Initiative， all kinds of tunnels are continuously constructed， and some engineering accidents also come one after another， especially the collapse of karst tunnels.In order to ensure the safety of tunneling. The risk assessment of collapse of karst tunnels has become a top priority. [Methods] Aiming at the shortcomings of fuzzy AHP which is insufficient for quantitative analysis， this paper intmJwkqrCpEzQeqhlRCA4gwg==roduces the Borda sequence value method in calculating the weight values， selects five indicators， including the level of surrounding rock， excavation span， depth of burial， groundwater， construction technology and management level， and establishes a karst tunnel collapse risk assessment model with the optimized fuzzy Borda sequence value method. [Findings] The optimized fuzzy AHP was used to assess the risk of collapse of the tunnel， and the final risk level was judged to be Class Ⅲ. [Conclusions] By introducing the Borda sequence value method， the subjectivity of the fuzzy AHP can be effectively reduced， and the risk level of tunnel collapse in karst area assessed by using the model is basically consistent with the actual situation of the case， which indicates that the model has good practicability.

Keywords： karst tunnel; risk assessment; fuzzy AHP; Borda sequence value method

0 引言

针对岩溶地区隧道工程塌方灾害的研究一直是业内最关注和最前沿的问题，其对铁路、公路、水利水电等重大工程领域的安全施工和防灾减灾具有重要意义。隧道建设不可避免地会遇到各种严峻的挑战，如地形复杂、地质条件恶劣等，特别是塌方的发生，极大地威胁着地下施工的安全［1］。

我国虽然在岩溶隧道风险评估方面起步较晚，但发展迅猛，尤其是近几年，随着云南、贵州、四川等地区铁路、公路隧道的修建，国内学者针对目前的发展趋势，着重对岩溶隧道风险管理进行了相关研究，大大降低了岩溶地区隧道的风险。李术才等［2］针对翻坝高速鸡公岭隧道的复杂岩溶环境，首次提出并成功实施了一种基于岩溶隧道施工风险动态评估的风险控制新机制；廖欣［3］采用多种评价方法，形成了一种较为实用的衡量因素危害的方法，并通过这种方法顺利对岩溶中可能发生的危害进行了评价；李志林等 ［4］在突水灾害研究中引入了小波神经网络，阐述了各类探测方法的优缺点，并多方面融合构建了一种新的探测方法；贾磊等［5］为解决隧道施工突水灾害因素繁多且相互关联的问题，提出利用模糊综合评价法来评判隧道突水风险；朱珍等［6］探讨了一种避免各种结果相互矛盾且专一性更强的理论来衡量岩溶隧道可能存在的危害，构建相应模型进行研究，并与实际工程情况相验证。吴贤国等［7］在武汉长江盾构隧道施工过程中，对长江隧道进行风险识别后，运用半定量的方法计算出了风险发生概率；郭威等［8］基于贝叶斯网络不确定性的推理，构建了岩溶隧道涌水风险的贝叶斯网络模型，并运用Netica软件的案例学习功能对统计数据进行分析，并结合地质雷达及红外探水手段进行研究。

综上所述，岩溶隧道塌方的风险性由危险性和危害性等两方面决定，其分别指发生灾害的可能性和造成的损失。然而，大多数研究都对隧道塌方的危险性进行了详细深入的分析，而对灾害的危害性研究较少。在研究方法方面，主要采用专家评判法、层次分析法（AHP）、模糊数学法等，但这些方法大都存在较多的主观因素影响、风险因素考虑不够全面、风险因素隶属函数的构造不够符合实际等问题，使得风险评估结果不够客观，在一定程度上偏离了实际情况，大大降低了评价结果的可信度［1］。

本文在前人研究的基础上，重点对岩溶隧道塌方风险评估进行研究，构建了模糊层次优化评估模型，并以某隧道为例，开展了岩溶隧道施工的风险评估工作，依据计算得到的风险等级，为施工提供指导，并且该方法可为其他岩溶隧道工程提供参考，具有一定的工程应用价值。

1 岩溶隧道塌方风险评估模型

1.1 隧道塌方风险因素辨识

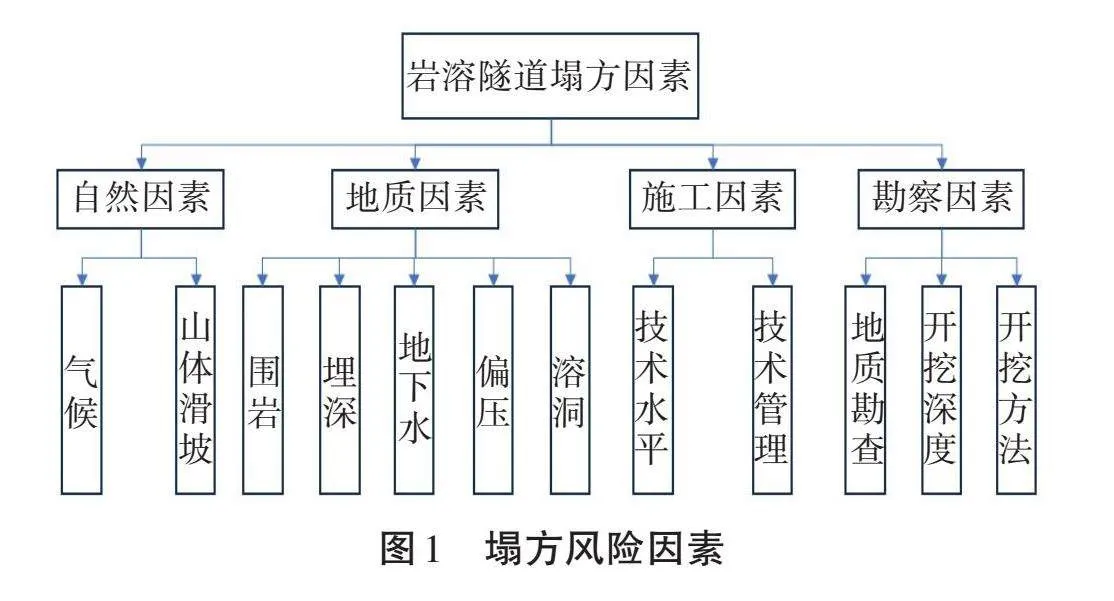
本研究根据现有文献、参考资料和已有的科研成果，在前人的基础上，得到影响塌方的各项因素指标如下。①自然条件影响：自然降雨、地震等；②地质条件影响因素：围岩的级别、埋深、地下水含量、是否存在偏压、有无断层破碎带等；③施工与管理条件影响因素：施工方技术水平、施工方管理水平等；④勘察设计影响因素：地质勘查是否准确合理、开挖方法选择的合理性、开挖跨度大小等。 通过分析，建立岩溶隧道塌方风险的因素解析图，如图1所示。

1.2 Borda序值法对模糊层次分析法的改进

目前，国内学者所运用的模糊层次分析法［9-10］都是建立在统计数据的基础上，存在很大的主观成分，因而使得隧道的风险评估基本是定性或半定量的评估。其中权重值的计算与专家的主观性密不可分，其是根据专家的经验以及对该风险因素的认知程度进行评判，因此需要对模糊层次法进行一定的优化，具体为改进第四步中权重值的确定，通过借鉴Borda序值法来计算各风险因子的序值，再通过层次分析法来确定各风险因子的权重，最后得出风险评价结果，具体步骤如下。

①建立因素集。因素集即包含所有风险要素，表示为式（1）。

[U=u1，u2，…，un] （1）

②建立评价集。评价集是把所有针对因子的评价整合起来，一般以程度语言或评定取值区间作为评价目标，表示为式（2）。

[V=v1，v2，…，vk] （2）

③确定函数的隶属度。在x对于y的隶属度中，以［0，1］区间的取值来度量x对y的重要程度。

④确定因素等级的权重值。本研究采用Borda序值法计算出不同风险因子间的重要性次序，结合这些风险因子的排序，将其反馈到层次分析法中的专家判断矩阵，使各风险因子的权重更加客观。其算法见式（3）、式（4）。

[B（Ri）=T=1Q（M−rin）， i=1，2，…，M] （3）

[rin=j：CNRi<CNRj， j=1，2，…，M] （4）

以上式中，i为某一特定指标；M为风险因子总数；Q为风险准则总数；[rin]为风险因子i在准则n下的风险等级；n是不同风险评价准则（本文构建的隧道塌方风险矩阵中有3个准则：本文设定当n=1时，表示风险影响；当n=2时，表示风险概率；当n=3时表示风险等级）；| |表示集合元素的个数。

Borda序值法的计算步骤：步骤1 ，确定M、Q的值；步骤2，确定风险Ri在评价准则N下的分值[CNRi]；步骤3，计算[rin]；步骤4，计算[B（Ri）]；步骤5， 计算[ORi]见式（5）；步骤6，输出风险[Ri]的排序[ORi]。

[ORi=M−j：BRi>BRj，j=1，2，…，M] （5）

将计算出的各风险因素的Borda值作为专家打分依据，由专家将风险因素进行两两比较，构建判断矩阵。

⑤一级模糊综合评价。将单因素的模糊评价，整合到一起，综合考虑所有基本风险因素的影响，得出对上一层次风险因素科学的评价结果，来处理好因素的模糊性。一级模糊矩阵见式（6）至式（8）。

[B=Ai·Ri=（ai1，ai2…aik）ri11……ri1n⋮⋱⋰⋮⋮⋰⋱⋮rik1……rikn][=（bi1，bi2，…bik）] （6）

[ bin=aijbijn] （7）

[B=B1⋮⋮Bn=b11……b1k⋮⋱⋰⋮⋮⋰⋱⋮bn1……bnk] （8）

⑥建立因素权重集。因素权重集反映的是各风险因素对于评价对象的影响程度，对于任一对象可定义权重为aij，则权重集见式（9）。

[A=a1，a2，…，an] （9）

其中因素的权重应满足归一化条件，见式（10）。

[1nai=1] （10）

相对量级可用等级表示，因而在运算时Ai可代入任意对象。

⑦二级模糊综合评价。一级模糊综合评价由于涉及因素较多，为了综合考虑各风险因素对最终评价结果的总体影响，需要进行二级模糊综合评价。对所有因素进行评价时，可得到模糊综合评价集见式（11）。

[C=A·B=（a1，a2，…，an）bi1……bik⋮⋱⋰⋮⋮⋰⋱⋮bn1……bnk] （11）

⑧评价结果。根据最大隶属度原则，取式（11）计算结果中的最大值对应评价集所对应的评价指标[Vl]，即为最终的评价结果。

1.3 风险指标分级标准

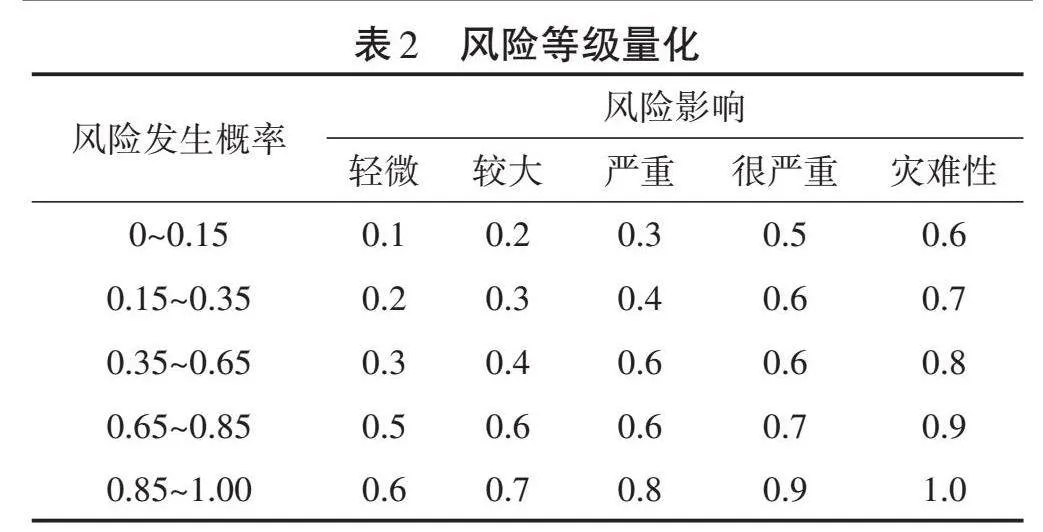
为了使模糊层次分析法更适用于岩溶隧道塌方风险评估工作，且评价结果更加精确，还需要对其中涉及的风险概率进行分级，对风险等级进行量化，主要改进结果见表1和表2。

经过对模糊层次分析法的优化，再根据上述详细步骤，可以建立一个隧道塌方风险模糊层次优化评估模型框架［11-12］，评估模型的实施过程如图2所示。

2 案例分析

2.1 工程概况

该隧道是永顺至吉首高速公路中的一座双洞单向交通隧道，全长1 010 m，该隧道所处地貌属于剥蚀溶蚀低山地貌，地形起伏大，山高坡陡，隧道轴线通过地面高程为430.60～567.10 m，相对高差约136.50 m，隧道最大埋深约127.44 m。山坡覆盖层较薄，基岩多出露，植被发育，主要为灌木、草丛。

2.2 隧道塌方风险评估

由于YK10+945～YK11+035段为浅埋偏压段，围岩中岩溶化程度高，溶蚀裂隙发育，甚至出现溶洞、落水洞等，围岩自稳能力差，雨季地表水沿岩溶裂隙和构造裂隙下渗，洞顶、洞壁可能产生淋雨状出水或股状出水，甚至出现塌方，因此有必要对该段进行塌方风险评估。

2.2.1 建立因素集。对该段进行详细的调查分析后，确定了5个主要因素，分别为：①围岩，该段全段经勘察后诊断为五级围岩，且在开挖掌子面处发现岩体较为破碎，多含大块孤石，含泥较多；②开挖跨度，此处隧道为双车道隧道，设计跨度为10.25 m，但由于所处山体岩体破碎且含泥，应做主要研究；③埋深，该段所处位置恰好为两山之间的山谷段，埋深较浅，隧道开挖后形成的自然拱不够稳定，地表植被发育，土壤松软；④地下水，该地区由于地理位置及气候原因，多雨且雨期持续时间长，而山体中裂隙发育，地表水容易顺着裂隙渗透进去；⑤施工技术与管理水平，由于资金跟技术水平有限，该隧道施工方能力并非国内顶尖水平，且施工工艺与管理与隧道施工安全息息相关，因此应重点考虑。

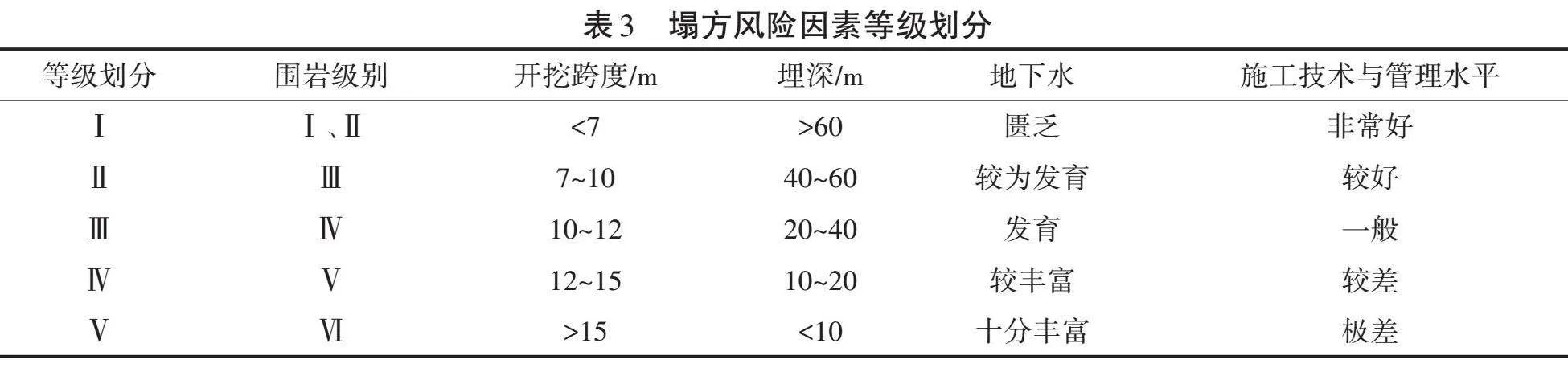
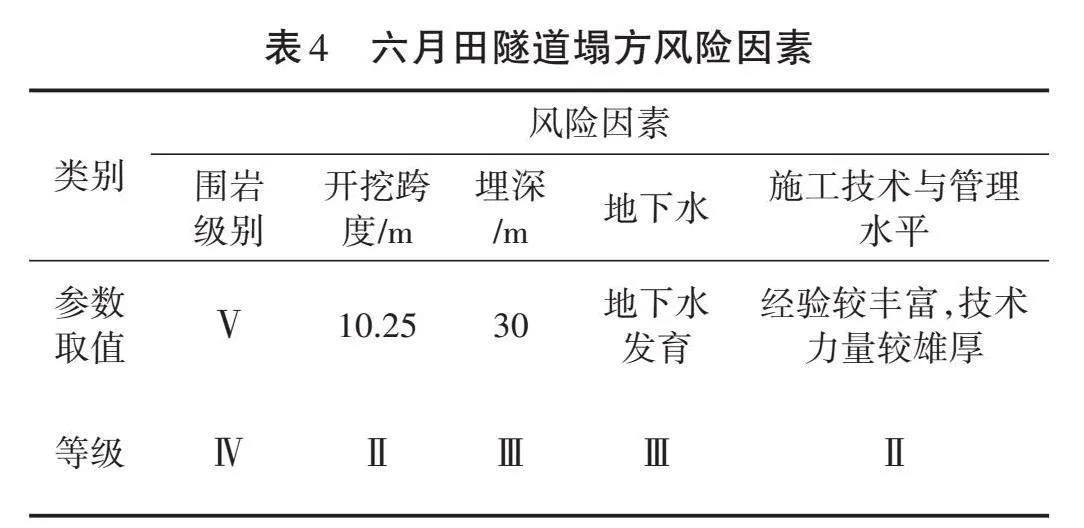
2.2.2 建立风险评价集。在判定风险时，为了使笼统性概念和不确定因素具体化，建立评价集为V=｛[v1，v2，v3，v4，v5]｝。一般用模糊语言进行描述，评价指标V为模糊评价的程度大小；[v1]为十分频繁发生，[v2]为很可能发生，[v3]为有可能发生，[v4]为很少发生，[v5]为不太可能发生。5个风险因素等级划分见表3。该隧道塌方风险因素等级划分，见表4。

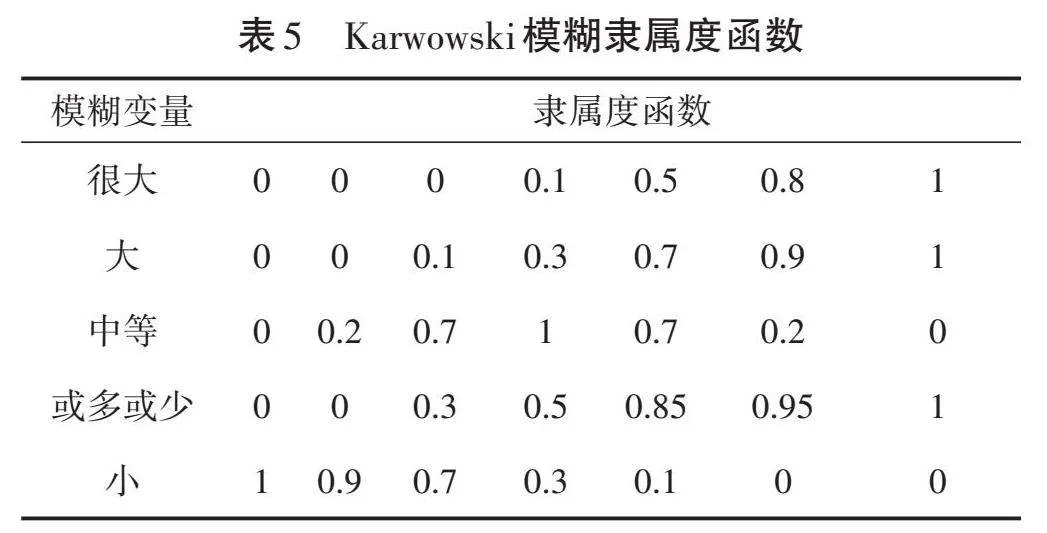
2.2.3 确定隶属度。对于不同对象的对应量级，可以赋予其一个定值，定值的大小表示优劣程度，把所有值综合起来制成函数表。可以借鉴工程风险分析上应用最多、最普遍的Karwowski［13-14］模糊隶属度函数，见表5。

本文对开挖跨度、埋深两个因素采用梯形隶属度函数，开挖跨度因素隶属度函数见式（12）至式（16）。

[μμ1（x）=0，x∈（0，7）x-78，x∈[7，15]1，x∈（15，+∞）] （12）

[μμ2（x）=0，x∈（0，7）⋃（15，+∞）x-75，x∈[7，12]1，x∈[12，15]] （13）

[μμ3（x）=0，x∈（0，7）⋃（15，+∞）x-73，x∈[7，10]1，x∈[10，12]15-x3，x∈[12，15]] （14）

[μμ4（x）=0，x∈（0，7）⋃（15，+∞）1，x∈[7，10]15-x5，x∈[10，15]] （15）

[μμ5（x）=1，x∈（0，7）⋃（15，+∞）15-x8，x∈[7，15]] （16）

埋深因素隶属度函数见式（17）至式（21）。

[μμ1（x）=1，x∈（0，10）⋃（60，+∞）60-x50，x∈[10，60]] （17）

[μμ2（x）=0，x∈（0，10）⋃（60，+∞）1，x∈[10，20]60-x40，x∈[20，60]] （18）

[μμ3（x）=0，x∈（0，10）⋃（60，+∞）x-1010，x∈[10，20]1，x∈[20，40]60-x20，x∈[40，60]] （19）

[μμ4（x）=0，x∈（0，10）⋃（60，+∞）x-1030，x∈[10，40]1，x∈[40，60]] （20）

[μμ5（x）=0，x∈（0，10）⋃（60，+∞）x-1050，x∈[10，60]] （21）

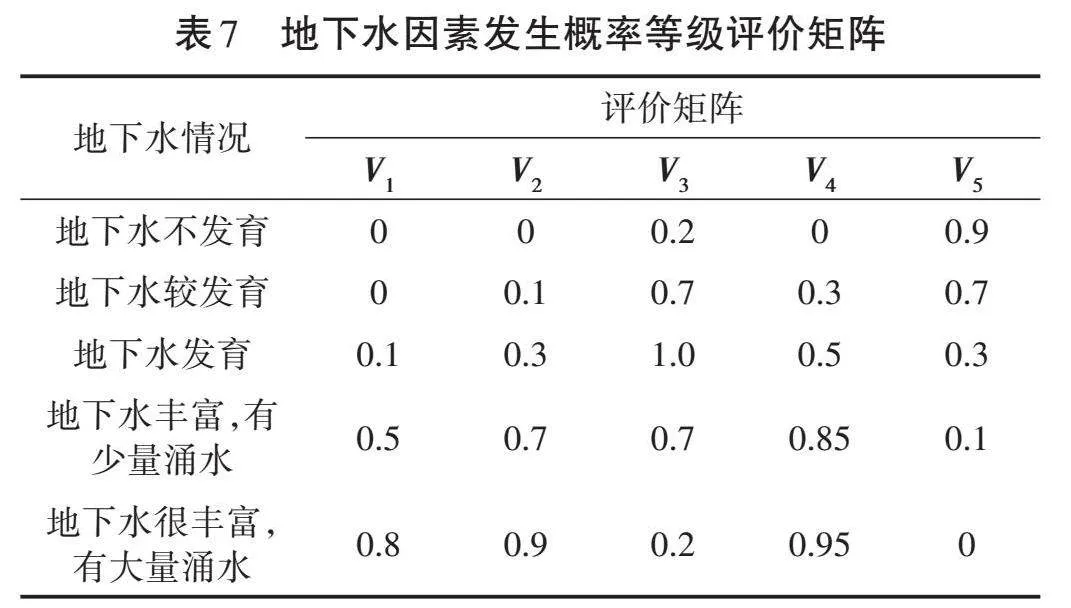
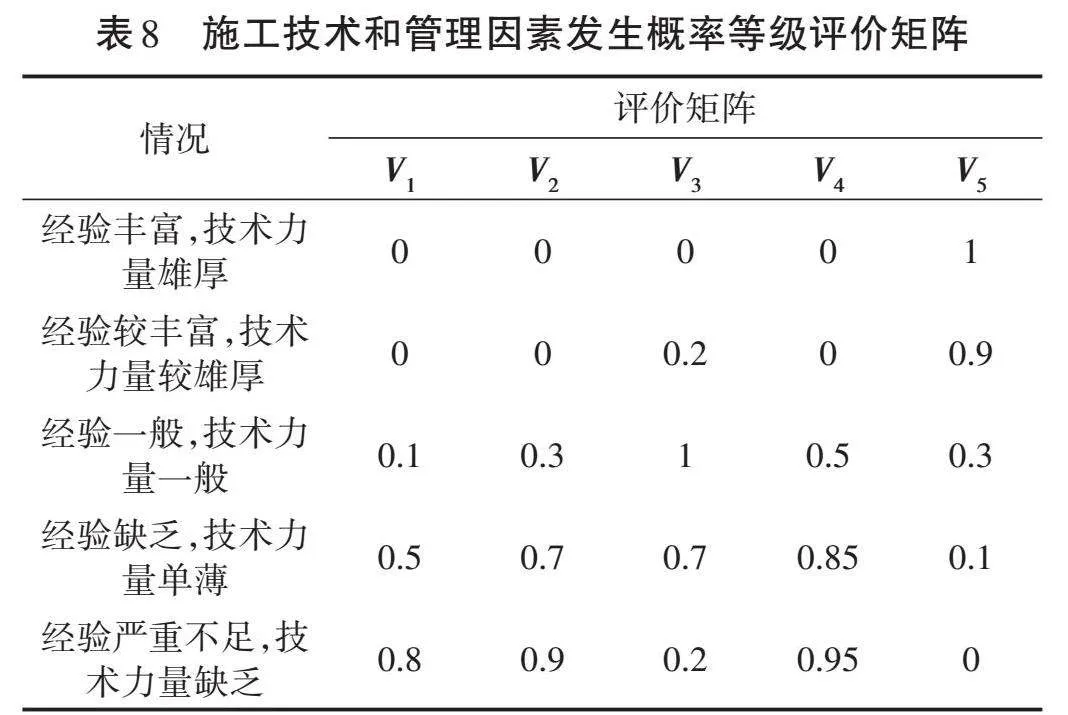
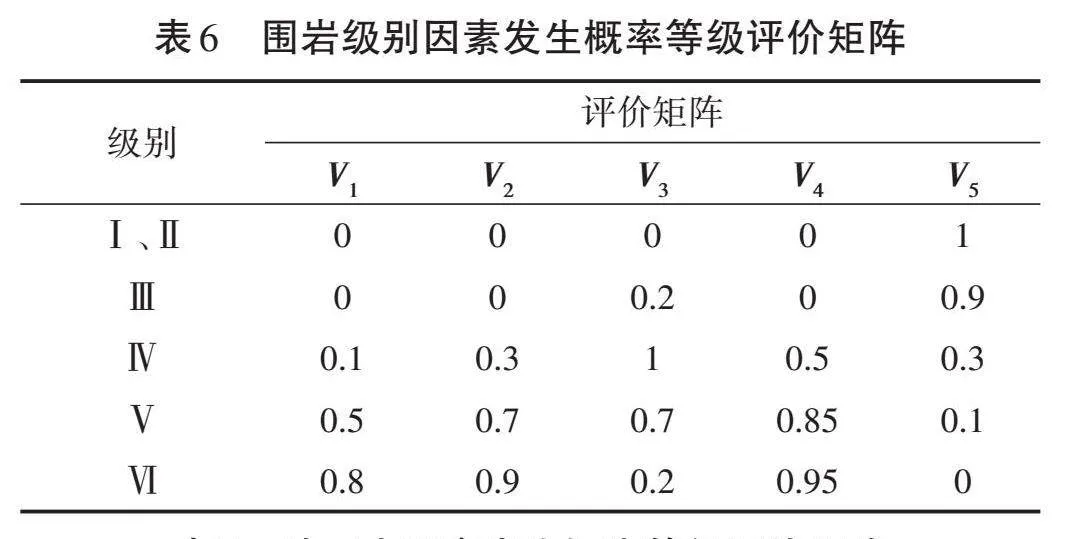
由于围岩地下水、施工技术和管理水平等3个因素为定性因素，因此只能采用Kaiwowski等［14］提出的在工程中常被采用的模糊隶属度评价矩阵进行分级，见表6至表8。

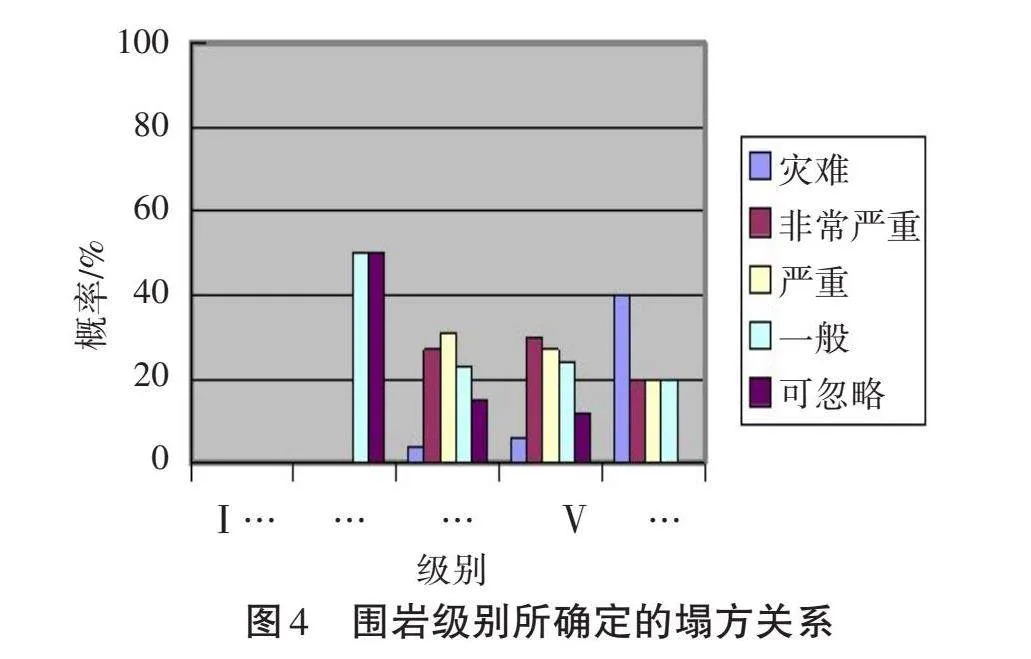
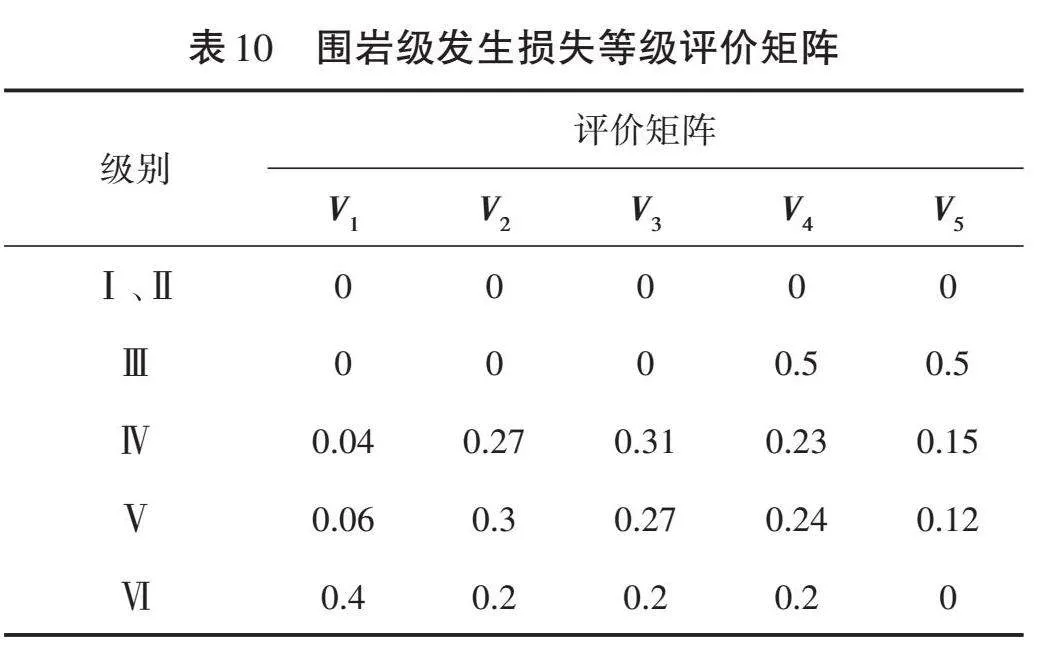
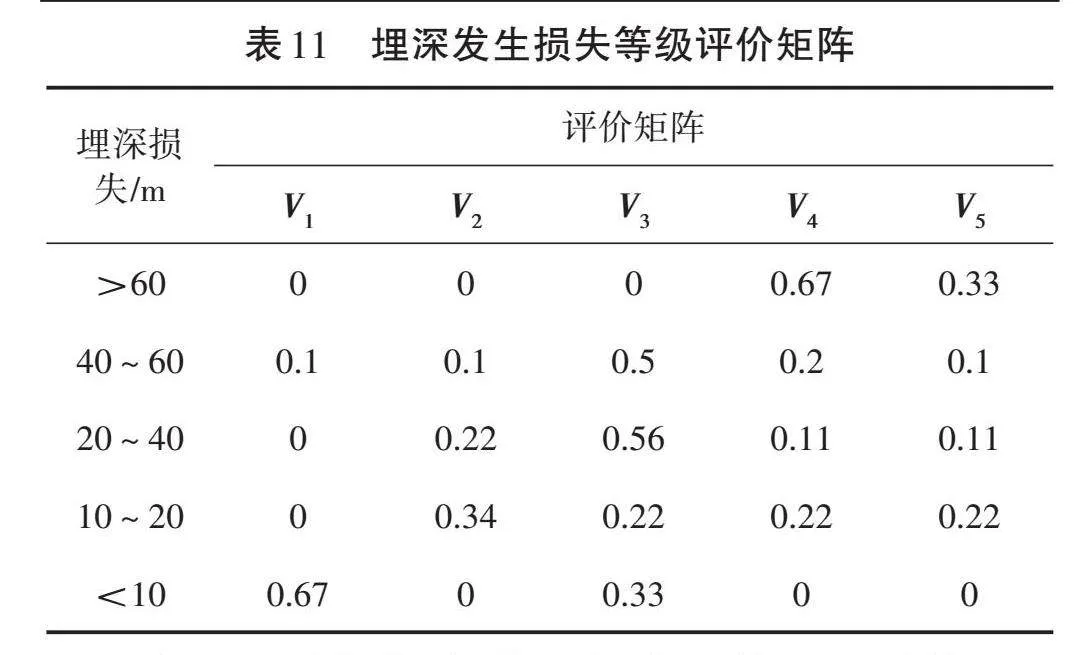
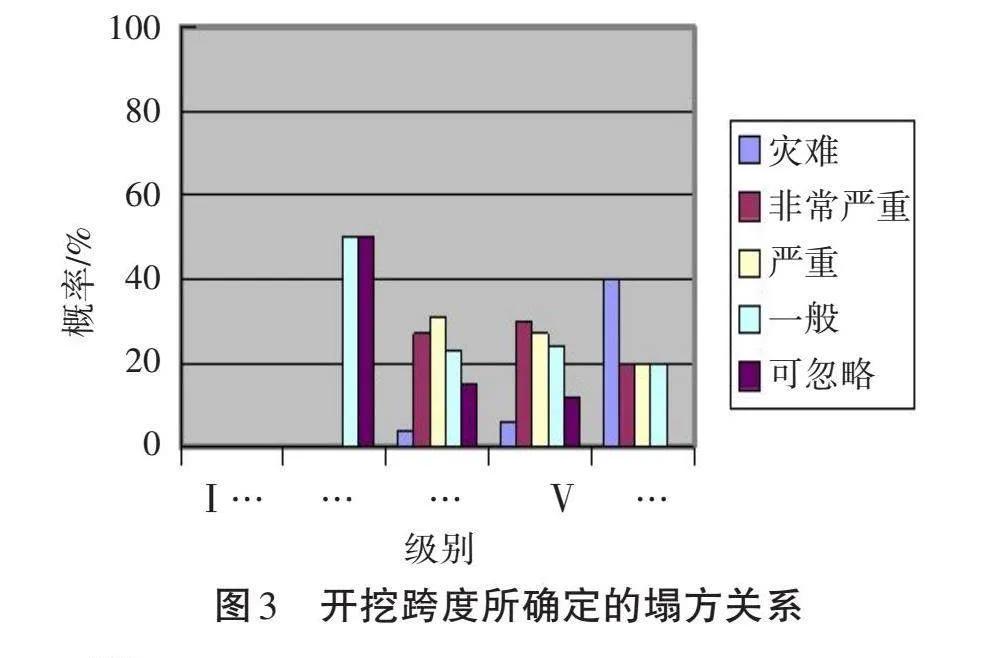
对于不可直接量化的对象，可采取一定的迂回方法，例如可以从塌方后的塌方量及直接经济损失来替代其不可确定的量级，即在对塌方量、直接危害和间接危害进行统计后，结合开挖跨度、围岩、埋深等3个因素关于塌方的概率直方图（图3至图5），进行类比分析得出其所产生的塌方损失而分别所得的等级矩阵。为保持塌方发生损失和塌方发生概率的因素一致，遂采用同样的因素集和因素等级划分来估算塌方损失。

由图可得出3个因素等级的隶属度，见表9至表11。

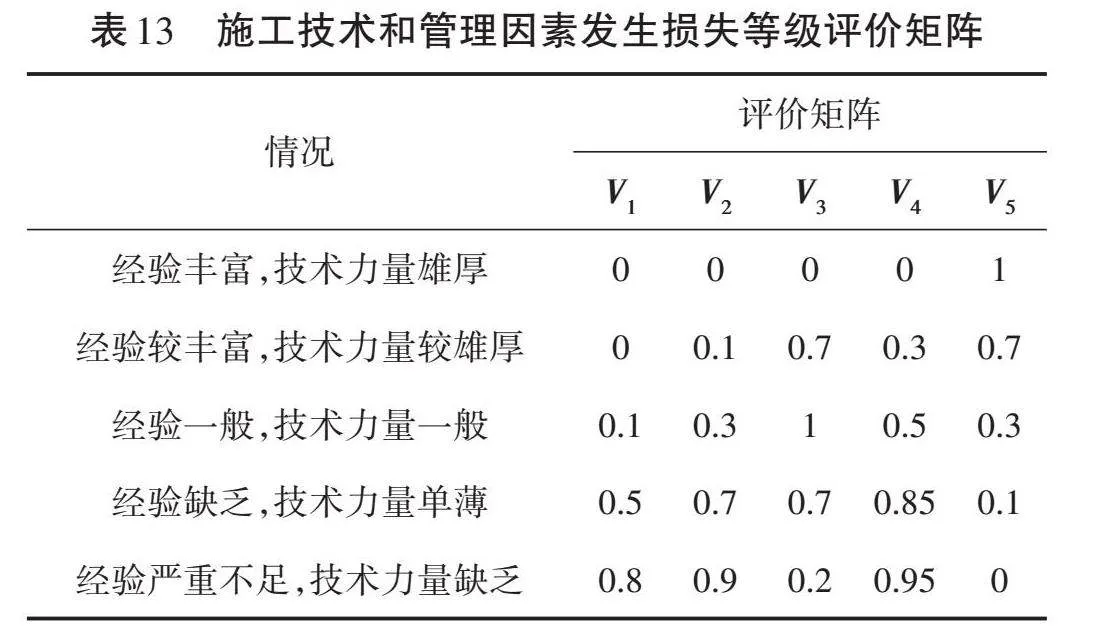
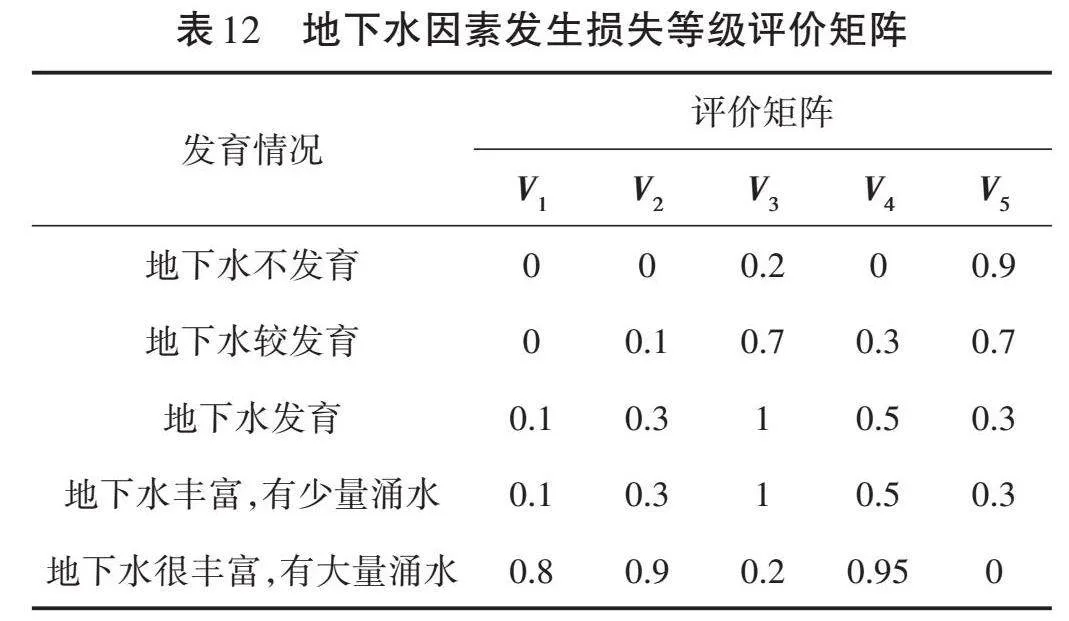
由于地下水状况、施工技术和管理水平等两个因素属于定性指标，无法进行数据统计，因此依然采用Karwowski等提出的隶属度函数来确定等级评价矩阵，具体见表12和表13。

通过建立的隧道塌方发生概率隶属度函数和等级评价矩阵，以及隧道塌方发生后果隶属度函数和等级评价矩阵，取所对应的向量组成，可得到该隧道塌方风险发生概率评价矩阵R1和发生后果评价矩阵R2分别见式（22）和式（23）。

[R1=0.50.70.70.850.10.410.651.00.950.590.60.751.00.670.40.10.31.00.50.300.10.70.30.7] （22）

[R2=0.060.30.270.240.120.050.260.260.370.0500.220.560.110.110.10.31.00.50.300.10.70.30.7] （23）

3 建立因素权重集

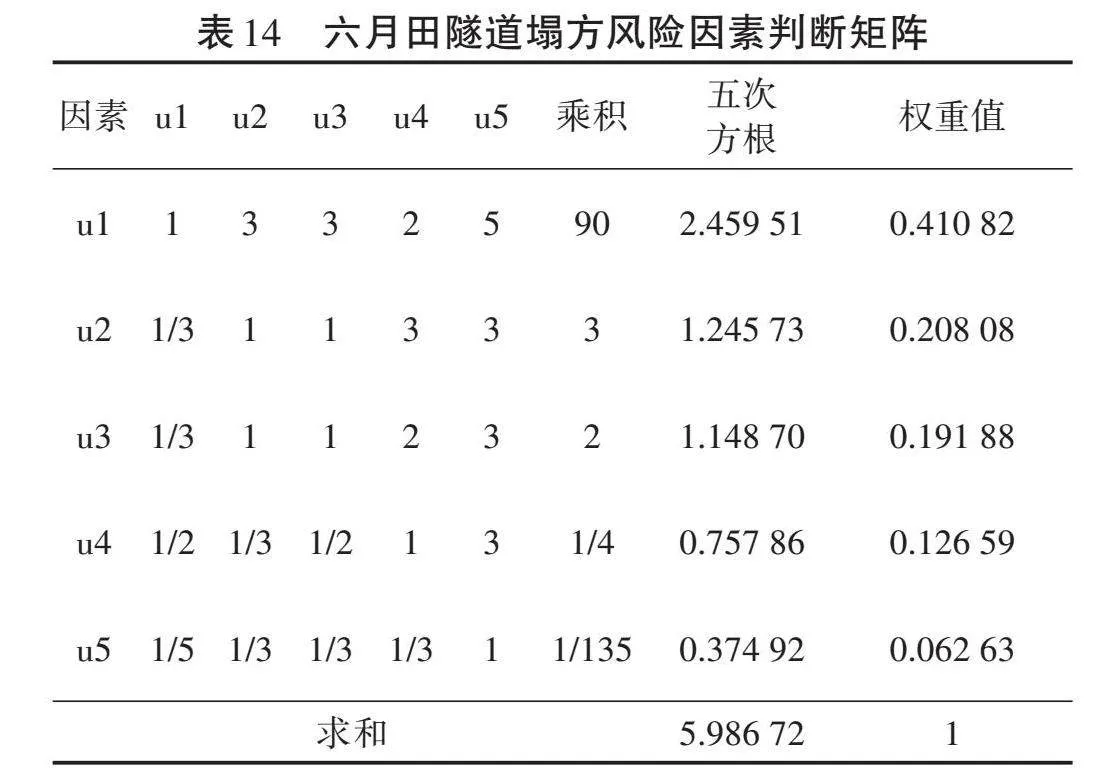
首先确定各风险因子Borda值、Borda序值。本文共选取了5个主要风险因子作为研究对象，各风险因子Borda值计算如下：[b1=k=13（N−rik）=5−r11+5−r12+5−r13=8]；[b2=][k=13（N−rik）=5−r21+5−r22+5−r23=5]；[b3=k=13（N−rik）=5−r31+5−r32+5−r33=11]；[b4=k=13（N−rik）=5−r41+5−r42+5−r43=4]；[b5=k=13（N−rik）=5−r51+5−r52+5−r53=7]。

根据上面得出的Borda值来计算该隧道塌方各个因素的权重，根据隧道实际情况由专家进行两两比较，从而构造出塌方风险综合判定矩阵，并采用方根法求得[λmax]和[ω]，见表14。

4 判断矩阵一致性检验及求二级模糊评价矩阵

进行一致性检验时，通过验证表14，运用式（24）至式（27）评估求得的评价矩阵是否满足性要求。

[λmax=i=1nCωinωi] （24）

[CI=λmaxn−1] （25）

[CR=CIRI] （26）

[CR≤ 0.1] （27）

根据表14计算得出因素权重集合为：[A1=A2=（0.41，0.21，0.19，0.13，0.06）]。

根据前文得出的R1、R2两个矩阵及得出的因素权重集，利用式（28），得出二级评价矩阵，YK10+945～YK11+035段为[C1=（0.42，0.61，0.86，0.76，0.32）]，[C2=]（0.05，0.26，0.44，0.28，0.16）。根据前文的最大隶属度法得出，塌方发生概率和塌方损失程度的等级同为Ⅲ级。

[C=A·B=（a1，a2…an）bi1……bik⋮⋱⋰⋮⋮⋰⋱⋮bn1……bnk] （28）

5 结论

经过计算得出YK10+945～YK11+035段隧道塌方发生概率和塌方损失程度的等级同为Ⅲ级；根据表2风险等级量化表，即可得到六月田隧道塌方风险等级为高风险（Ⅲ级）。

本文在风险概率、风险影响，风险等级等三方面对六月田隧道塌方风险进行了研究。分析结果可知，六月田隧塌方风险的主要风险因子为围岩级别、地下水、开挖跨度、埋深、施工技术与管理水平等，再利用优化后的模糊层次分析法对六月田隧道进行塌方风险计算各风险因素权重值，建立风险因素评价集，最后得出风险总值，确定了风险等级为Ⅲ级，说明本项目必须采取风险应对措施，以把风险造成的负面影响降到最低。

参考文献：

［1］朱建群，李天正.基于突变理论的岩溶隧道突水突泥风险评估模型及其应用研究（英文）［J］. Journal of Central South University，2020，27（5）：1587-1598.

［2］李术才，周宗青，李利平，等. 岩溶隧道突水风险评价理论与方法及工程应用［J］. 岩石力学与工程学报［J］.2012（9）：1858-1867.

［3］廖欣. 基于层次分析法的铁路隧道岩溶风险评估与处理措施研究［J］. 四川建筑，2011（3）：90-92.

［4］李志林，王星华，谢李钊.基于模糊小波神经网络的岩溶隧道风险评估及综合超前地质预报技术［J］.现代地质，2013，27（3）：719-726.

［5］贾磊，李源，章岩.隧道突水突泥灾害的模糊预测和控制措施［J］.灾害学，2014，29（2）：69-71.

［6］朱珍，王旭春，袁永才，等.基于加权平均法的岩溶隧道突涌水风险评估［J］.公路工程，2015（6）：51-54.

［7］吴贤国，吴刚，骆汉斌.武汉长江隧道工程盾构施工风险研究［J］.中国市政工程，2007（1）：51-53.

［8］郭威，陈秋南，阳跃朋，等.基于贝叶斯网络的岩溶隧道涌水风险评估［J］.工程地球物理学报，2017，14（1）：20-25.

［9］詹润涛.层次分析法判断矩阵可靠性探讨［J］.数学的实践与认识，2009，39（21）：122-128.

［10］孙锡玉.模糊数学及其应用［M］.武汉：武汉大学出版社，2002.

［11］王卓甫，陈登星.水利水电施工进度计划的风险分析［J］.河海大学学报，1999，27（5）：87-89.

［12］李洪兴.工程模糊数学方法及应用［M］.天津：天津科学技术出版社，1993.

［13］KARWOWSKI W， MITAL A.Applications of approximate reasoning in risk analysis［J］.Advances in Human Factors/Ergonomics，1986，6：227-243.

［14］谢季坚，刘承平.模糊数序方法及其应用［M］.3版.武汉：华中科技大学出版社，2006：37-46.