基于瓦斯风险预警的最佳逃生路线计算系统

摘 要：【目的】瓦斯爆炸事故是煤矿面临的重大安全隐患之一，考虑到煤矿井下环境的复杂性以及瓦斯灾害发生时环境的突变性，优化逃生路径变得至关重要。【方法】通过LSTM模型实现对井下各节点瓦斯浓度的预测，并结合逻辑回归模型判别该节点是否存在风险，根据判别结果实时更新巷道拓扑结构，实现基于预测结果的最优避灾路线规划。【结果】该系统重新生成的最佳逃生路线更加科学、有效，可为井下人员提供更加安全、可靠的逃生路线。【结论】在模型的综合作用下，路线规划更加合理，增加了人员逃生成功的概率。

关键词：瓦斯浓度；LSTM模型；逻辑回归模型；避灾路线；动态调整

中图分类号：TD712 文献标志码：A 文章编号：1003-5168（2024）16-0017-05

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.16.004

The Best Escape Route Calculation System Based on Gas Risk Warning

DING Weiyou LIU Xiaoli

（North China University of Science and Technology， Tangshan 063000，China）

Abstract： [Purposes] Since gas explosion accident is one of the major safety hazards faced by coal mines， optimizing escape routes has become crucial due to the complexity of the underground environment in coal mines and the sudden changes in the environment during gas disasters.[Methods] The best escape route regenerated by this system is more scientific and effective， providing reliable escape routes for underground personnel， which will effectively increase the probability of escape for underground personnel.[Findings] The best escape route regenerated by the system is more scientific and effective， which can provide safer and more reliable escape routes for underground personnel.[Conclusions] Under the comprehensive effect of the model， route planning is more reasonable， and finally increases the probability of success of personnel escape.

Keywords： gas concentration; LSTM model; logistic regression model; disaster avoidance route; dynamic adjustment

0 引言

我国作为世界能源大国，能源结构在相当长的时间内以煤炭为主，煤炭的消耗量占一次性能源构成的70%以上［1］。煤矿瓦斯是煤层开采过程中产生的高危气体，主要由甲烷、二氧化碳、氮气等组成，瓦斯爆炸事故是煤矿面临的重大安全隐患之一。

生产矿井通常根据已有经验、实际情况和灾害种类提前制定应急预案，规划避灾路线。对于井下工作人员，在事故发生后选择正确、合理的避灾路线可以大大提高生还概率。然而，由于矿井下巷道环境的复杂性以及灾害发生时环境的突变性，既定避灾路线很可能已经不是当前的最优路径，按照既定路线逃生很有可能会有新的危险。因此，许多专家、学者在避灾路线规划方面展开了诸多研究。徐志奇［2］根据井下有害气体蔓延趋势，并结合实时监测得到的有害气体浓度、风向等数据，生成动态的避灾路线；杨林等［3］探讨了井下瓦斯突出前后最佳避灾路线的异同，利用Dijkstra算法求解最佳路径，指导人员逃生；黄运爽等［4］通过综合考虑影响工作人员正常通行的因素（包括巷道因素和灾害因素），以求得最短逃生时间为目标，构建避灾模型，规划避灾路线；郭昕曜［5］探讨了瓦斯爆炸直接伤害、次生伤害与避难硐室的位置关系，基于Flody算法分析了最优疏散路径。尽管以上研究考虑了有害气体蔓延趋势、爆炸次生灾害等因素对最优逃生路径的影响，但仍然是建立在固有模型的基础上，无法根据实际情况和潜在危险进行实时调整［6］。

本研究针对既定逃生路线无法根据井下实际情况和潜在危险进行自动调整的局限，提出融合LSTM瓦斯浓度预测、逻辑回归风险判别、Dijkstra路径规划等方法，实现井下最佳逃生路线的规划。具体而言，首先，基于LSTM模型实现井下瓦斯浓度变化趋势的预测；其次，基于逻辑回归风险判别模型对预测数据进行分析，判断是否存在潜在风险；最后，基于Dijkstra算法更新最优逃生路线，指导井下人员快速地逃生。

1 基于LSTM模型构建瓦斯浓度预测模型

1.1 LSTM模型

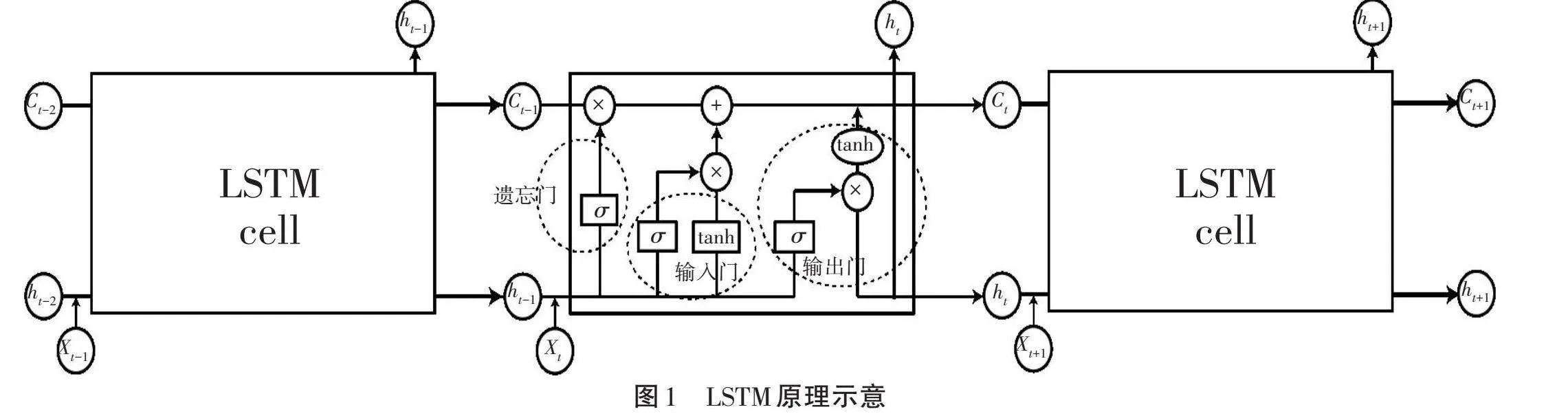
长短期记忆（Long short-term memory， LSTM）模型是RNN模型的变体，与经典RNN相比能够有效捕捉长序列之间的语义关联， 缓解梯度消失或爆炸现象。LSTM的关键在于神经单元的信息状态，神经单元的信息流传通过遗忘门、输入门、输出门控制，其中遗忘门的任务是筛选细胞状态中的信息，并将信息有选择性地遗忘 ［7-8］，其公式见式（1）、式（2）。

[ft=sigmoidWf∙ℎt−1， xt+bf] （1）

[Ct=tanhWc∙ℎt−1， xt+bc] （2）

式中：[ft]为遗忘门；[xt]为时刻[t−1]神经元的输入；[ℎt−1]为时刻[t−1]神经元的输出；[Wf]代表遗忘门权重矩阵； [bf]代表遗忘门阈值向量；sigmoid为神经元激活函数； [Ct]为t时刻的新信息；[Wc]代表单元信息更新权重矩阵； [bc]代表单元信息更新阈值向量；tanh为双曲正切函数。LSTM原理示意如图1所示。

输入门的功能是有选择地记录新的信息到细胞状态，并决定储存哪种新信息到细胞状态（单元模块）中。输入门包括sigmoid层和tanh层，sigmoid层确定何值的更新，tanh层生成新的候选记忆，添加补充丢弃的属性信息。其公式见式（3）、式（4）。

[it=sigmoidWi∙ℎt−1， xt+bi] （3）

[Ct=ft∙Ct−1+it∙Ct] （4）

式中：[it]为输入门；[Ct]为更新后的单元信息状态；[Wi]代表输入门权重矩阵；[bi]代表输入门阈值向量；[it]决定[Ct]是否加入t时刻状态。

将二者进行乘积，从而获得最终输出信息。其公式见式（5）、式（6）。

[ot=sigmoidWo∙ℎt−1，xt+bo] （5）

[ℎt=ot∙tanh（Ct）] （6）

式中：[ot]为输出门；[Wo]代表输出门权重矩阵； [bo]代表输出门阈值向量；[ℎt]为输出门最后的输出。

1.2 瓦斯浓度预测

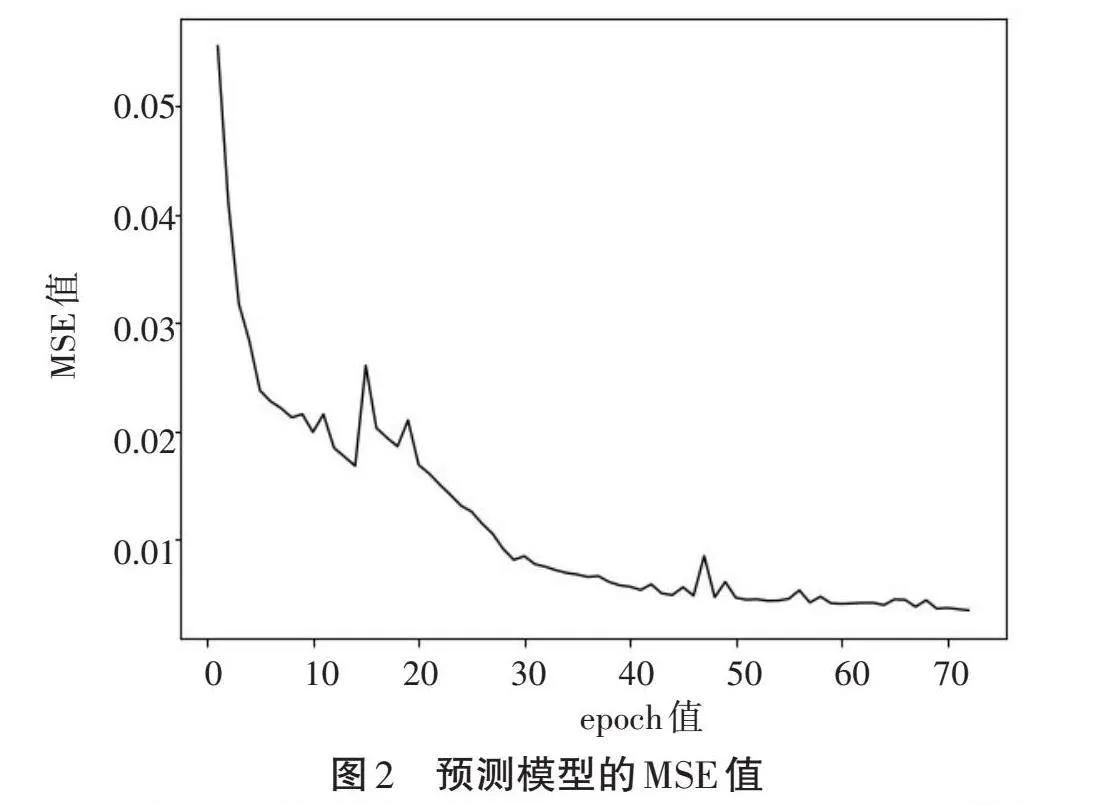
选取贵州某煤矿20916掘进工作面2012年12月15日0时至2012年12月18日13时这一时间段内，采集的800条以5 min/次为间隔的瓦斯浓度原始监测数据作为试验数据［9］。将数据库中70 %的数据作为训练集，30 %作为测试集。对于LSTM模型，本研究设置隐藏层数目为4，隐藏层节点单元数目为75，激活函数选择线性函数。权值初始化采用Xavier方法，利用Adam算法优化梯度下降的过程。采用均方误差（MSE）作为评价指标，定义为[MSE=1ni=1n（yi−yi）2]，其中[yi]为实际值，[yi]为预测值。如图2所示，经过训练，预测模型的MSE从最初的0.055降低到了0.0003。

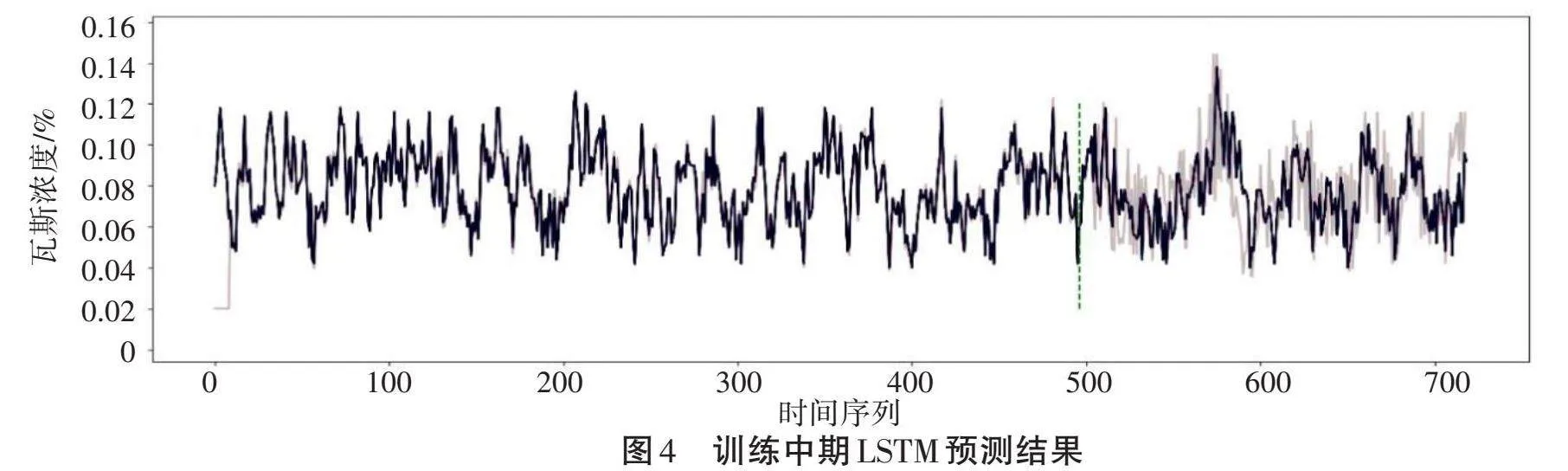
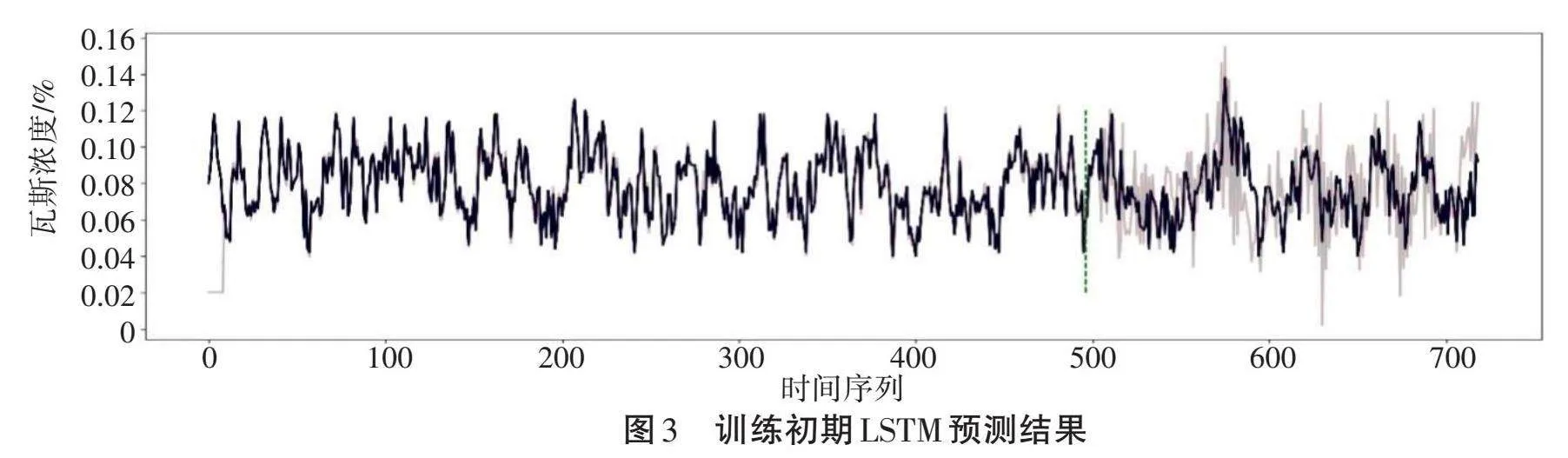
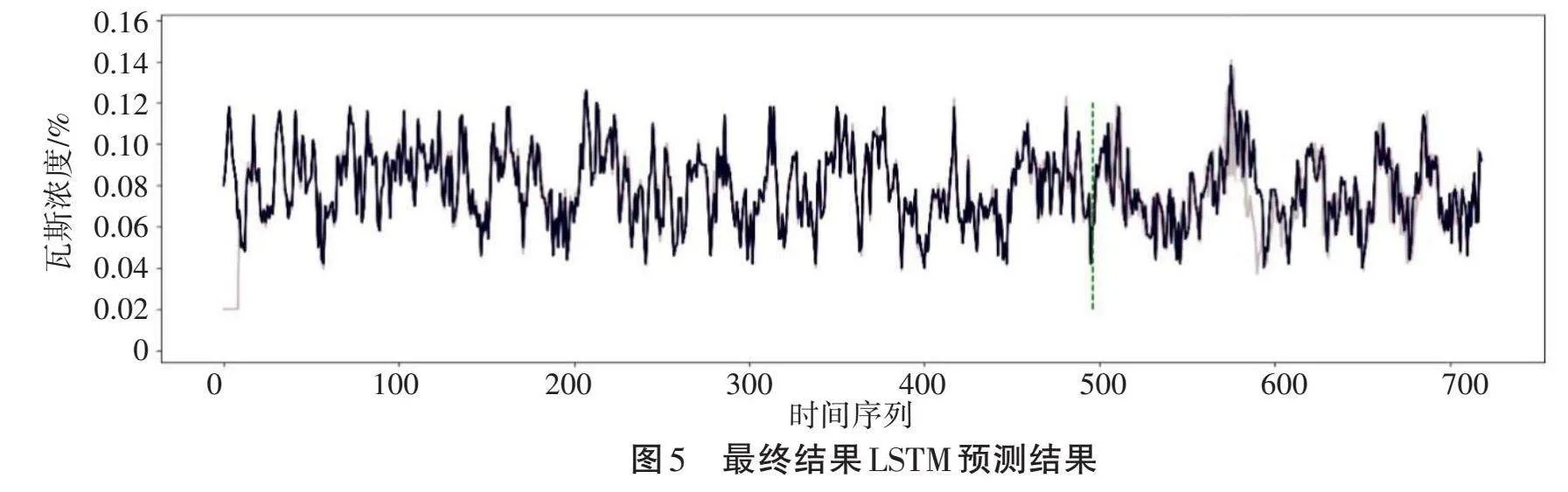
图3是训练初期（epoch=10，MSE=0.021）的结果，黑色为真实值，灰色为预测值。可以看到，此时训练集有了初步拟合，但是对于测试集，预测值和真实值仍有很大差距。图4是训练中期（epoch=40，MSE=0.020）的结果，可以看到此时训练集和测试集的效果都有了进一步提高。图5是训练最终结果（epoch=72，MSE=0.0003），可以看到此时测试集准确率趋于稳定不再上升。结果表明，经过训练的LSTM模型可以有效预测该地点下一时刻气体中瓦斯浓度的值。

2 基于逻辑回归模型实现风险判别

逻辑回归（ Logistic Regression） 是一种广义的线性回归分析模型，假设[yx]服从伯努利分布，且自变量x与因变量y存在线性关系。逻辑回归通过sigmoid函数引入了非线性因素，是一种用于解决二分类（0/1分类）问题的机器学习方法［10］。

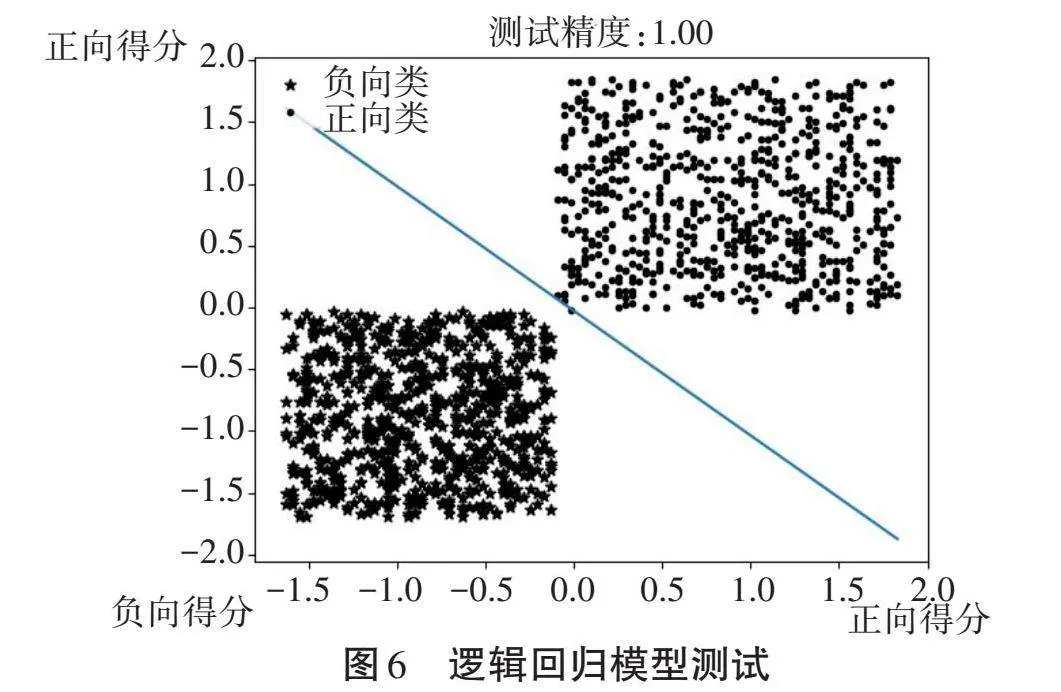
本研究将上述数据中80%的数据作为训练集，20%的数据作为测试集。当工作面的瓦斯浓度数据异常但未达到报警浓度为1%的阈值，通过逻辑回归模型对数据进行分析。异常数据为正向类，正常数据为负向类。在求解模型的过程中，定义了sigmoid作为激活函数，定义交叉熵作为损失函数，选用梯度下降法求解模型参数（alpha=0.001，迭代次数=15 000）。图6展示了经过训练的模型在测试集上的表现，预测准确率为100%。

3 基于Dijkstra算法更新最优逃生路线

3.1 构建井下巷道带权重拓扑图

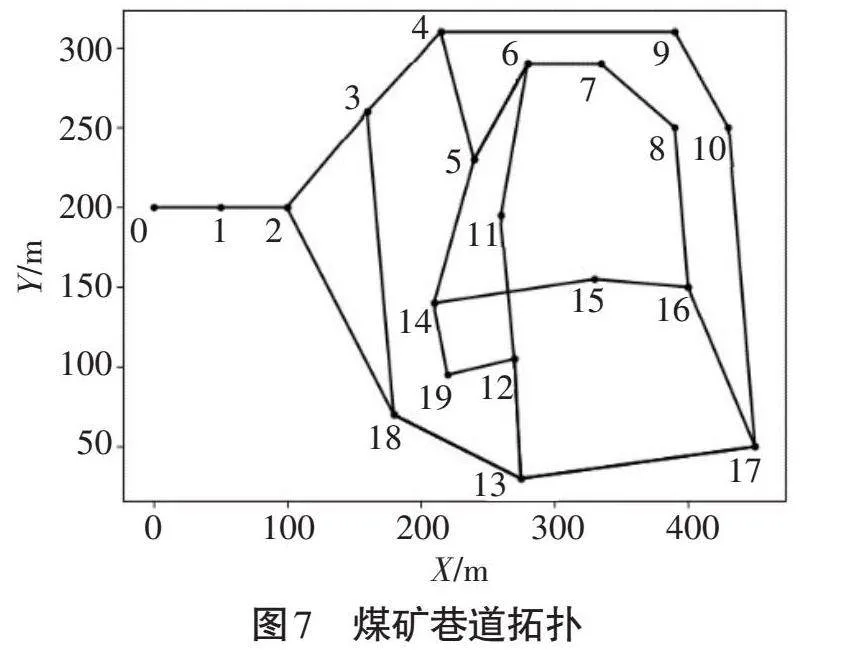
本研究使用煤矿巷道的拓扑图为逃生路线规划示意图，巷道拓扑如图7所示。图中点12、15、16为避难硐室。

拓扑图中线段长度代表巷道长度，但逃生路线规划并不能仅依赖于巷道长度，而是一种融合巷道逃生困难程度的当量长度。各路段当量长度见表1。

3.2 基于Dijkstra算法规划避灾路线

Dijkstra算法是一种典型的基于贪心策略的最短路径规划算法，用于计算一个节点到其他所有节点的最短路径，常用于解决非负权重图的单元最短路径问题。该算法的核心思想是将图所有点的集合S分为2部分，V和U。V集合是已经得到最短路径的点的集合，在初始情况下V中只有源点s；U集合是还未得到最短路径点的集合，在初始情况下是除s的所有点。因为每次迭代需要指明当前正在迭代的V集合中的某点，所以将该点设为中间点。因此应先将s设为中间点k，再开始迭代。在每一次迭代过程中，取得U中距离k最短的点k，将k加到V集合中，将k从U集合删除，并设为中间点v。重复此过程直到U集合为空［11］。

本研究中，为了实现根据井下实际情况及潜在危险情况进行避灾路线的自动调整，将先根据上述LSTM模型预测的各个节点的瓦斯气体浓度和风险识别结果对拓扑图进行更新，再基于Dijkstra算法更新最佳逃生路线。具体而言，正常情况下，巷道权重为距离长度，一旦出现风险识别结果为高风险的情况，则该节点巷道权重记为无穷大，判定相应路段可能无法安全通行，随后进行路径重新计算与修正提示。

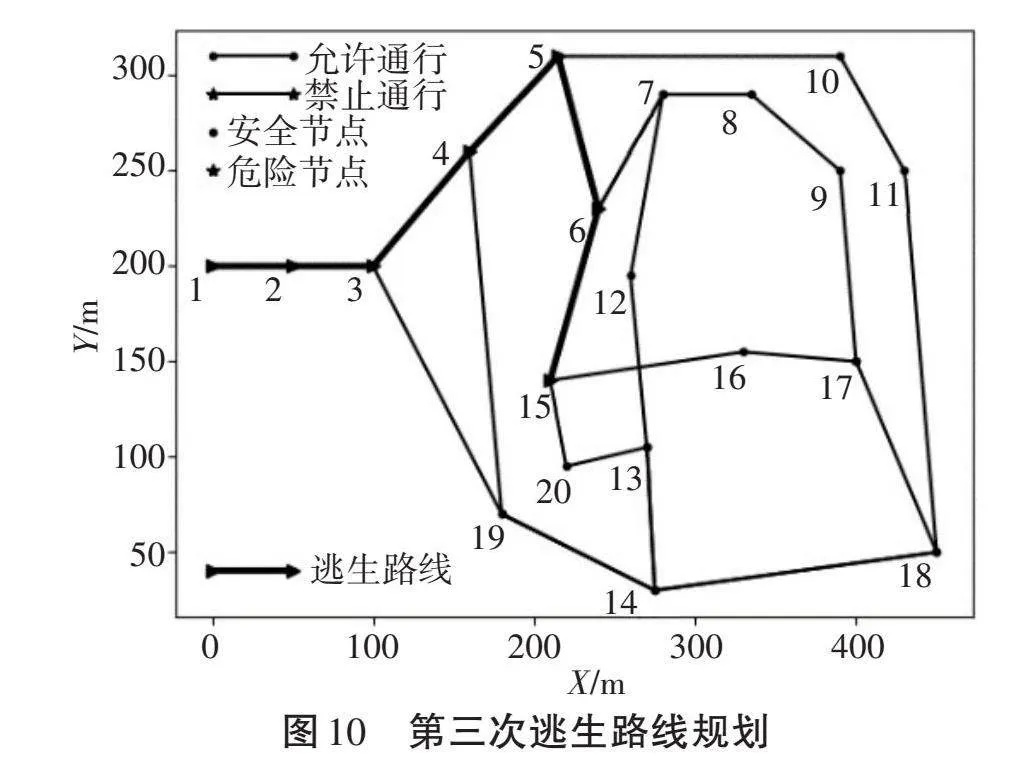
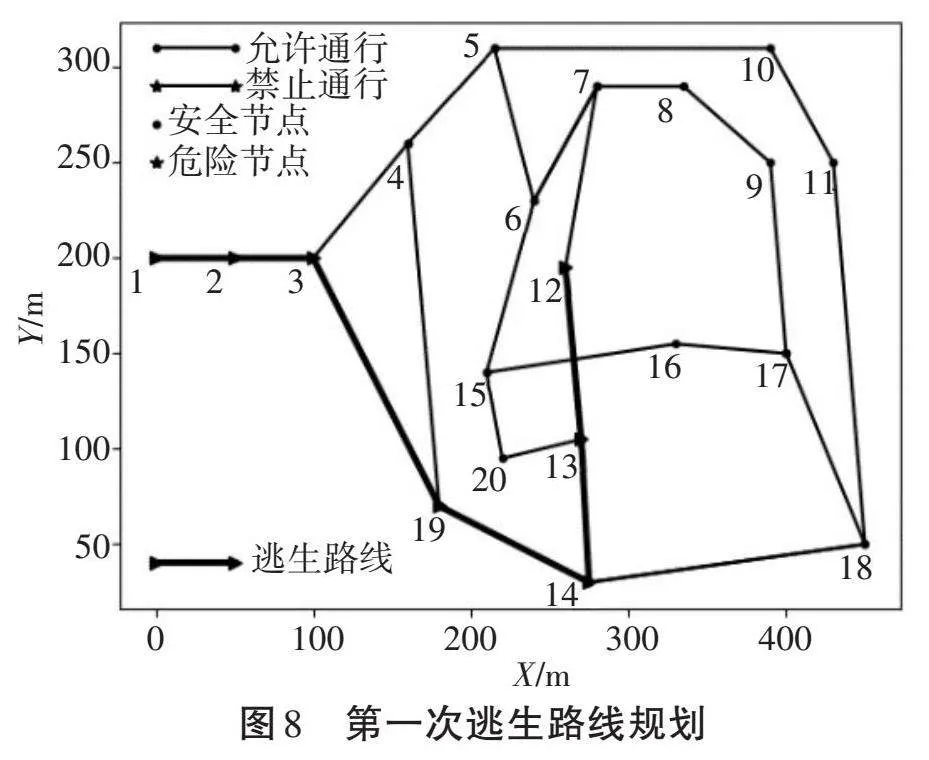
如图8所示，井下危险发生后，系统提示井下人员最佳逃生路线为1—2—3—19—14—13—12；然而在下一时段，系统经过动态刷新，判断路线3—4及路线19—14有危险预警，此时系统更新最佳逃生路线为1—2—3—19—4—5—6—7—12，逃生路线如图9所示；如果点12不能再作为安全避难点，系统自动规划其临近的点15为最终目标，此时更新逃生路线为1—2—3—4—5—6—15，逃生路线如图10所示；同理，若下一时段系统检测到路线3—4及路线19—14有危险预警，将重新规划路线为1—2—3—19—4—5—6—15，逃生路线如图11所示。如果点12、点15都不能再作为安全避难点，系统将选定距离较远的点16作为最终目标，并以类似上述方式进行路线规划。经过重复试验表明，融合了预测模型输出和风险判别模型输出的系统，重新生成的最佳逃生路线科学、有效，能够为井下人员提供可靠的逃生路线，将有效提高井下人员脱险的概率。

4 结论

针对煤矿井下瓦斯浓度危险性对工作人员带来的潜在危险，本研究通过LSTM模型实现对井下各节点瓦斯浓度的预测，并结合逻辑回归模型判别该节点是否存在风险，进而根据判别结果实时更新巷道拓扑结构，从而实现基于预测结果的最优避灾路线规划。模拟结果表明：①在瓦斯浓度预测模型和风险判别模型的综合作用下，可以使得路线规划更加合理，增加人员逃生成功概率；②该系统可以最大限度地减少因逃生过程中危险规避不及时造成的人员伤亡和财产损失。

参考文献：

［1］刘业娇，袁亮，薛俊华，等. 2007—2016年全国煤矿瓦斯灾害事故发生规律分析［J］. 矿业安全与环保，2018，45（3）：124-128.

［2］徐志奇. 井下瓦斯蔓延趋势分析与避灾路线动态规划方法［J］. 内蒙古煤炭经济，2017（13）：128-129.

［3］ 杨林，刘勇，江成玉. 煤与瓦斯突出后最佳避灾路线的研究［J］. 煤炭技术，2014，33（12）：213-215.

［4］ 黄运爽，刘阳，张良良，等. 煤矿采场灾害人员疏散模型及避灾硐室布置［J］. 煤矿安全，2017，48（6）：112-115.

［5］ 郭昕曜. 高突矿井瓦斯风险评估方法与管控技术研究［D］.武汉：武汉理工大学，2019.

［6］赵慧敏，李超，曾庆田.煤矿井下应急逃生最优路径规划算法研究综述［J］.软件导刊，2018，17（5）：1-5.

［7］ 荀晓玉，苏璨，李威，等. 基于CNN-LSTM的煤矿瓦斯浓度预测［J］.现代信息科技，2020，4（20）：149-152.

［8］ 刘莹，杨超宇. 基于多因素的LSTM瓦斯浓度预测模型［J］. 中国安全生产科学技术，2022，18（1）：108-113.

［9］ 张震，朱权洁，李青松，等. 基于Keras长短时记忆网络的矿井瓦斯浓度预测研究［J］.安全与环境工程，2021，28（1）：61-67，78.

［10］ 廖英雷. 基于逻辑回归模型的瓦斯浓度异常值检测与预警［J］. 陕西煤炭，2020，39（4）：13-18，44.

［11］ 康宁. 基于改进Dijkstra算法的煤矿井下应急路径规划研究［D］.西安：西安科技大学，2020.