基于卷积神经网络的主网继电保护在线整定方法

摘 要：【目的】受主网故障状态的多样性和整定规则的适应性影响，继电保护的闭环阶跃响应振幅难以得到有效控制，为此，提出了基于卷积神经网络的主网继电保护在线整定方法。【方法】将主网中的同种保护功能涉及的定值变量作为一个集合，并构建主网继电保护在线整定数学模型。在开展具体的主网继电保护定值设置阶段，引入卷积神经网络，利用损失函数，计算在随机梯度下降机制下的最优正则化继电保护定值。【结果】测试结果表明，该方法测试的电网继电保护在闭环阶跃响应的振幅在50 s以内实现了快速收敛，且相较于对照组而言更加平稳。【结论】该方法在闭环阶跃响应方面取得了显著的优势，不仅提高了系统的收敛速度，而且改善了系统的振幅稳定性。有助于提升电网继电保护系统的运行效率和可靠性，具有实际的应用价值和推广潜力。

关键词：卷积神经网络；主网继电保护；在线整定；数学模型；定值设置；损失函数；随机梯度；最优正则化

中图分类号：TP262 文献标志码：A 文章编号：1003-5168（2024）16-0013-04

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.16.003

Online Tuning Method of Main Grid Relay Protection Based on

Convolutional Neural Network

YANG Zhongzhe LIU Yanbo CHEN Jia JIN Wanglei

（State Grid Shanghai Fengxian Power Supply Company， Shanghai 201499， China）

Abstract： [Purposes] Due to the diversity of fault states of the main grid and the adaptability of the setting rules， the closed-loop step response amplitude of the relay protection is difficult to be effectively controlled. Therefore， an online setting method for the relay protection of the main grid based on convolutional neural network is proposed. [Methods] The same protection function in the main grid is taken as a set of fixed value variables， and the online setting mathematical model of the main grid relay protection is constructed. In the specific setting stage of the main grid relay protection， convolutional neural network is introduced， and the loss function is used to calculate the optimal regularization relay protection setting under the stochastic gradient descent mechanism. [Findings] In the test results， the amplitude of the closed-loop step response of the test grid relay protection under the design method not only realized rapid convergence within 50s， but also was more stable than that of the control group. [Conclusions] It is shown that the design method has a significant advantage in the closed-loop step response， which not only improves the convergence speed of the system， but also improves the amplitude stability of the system，which is helpful to improve the operation efficiency and reliability of power grid relay protection system， and has the potential of practical application and popularization.

Keywords：convolutional neural network; main grid relay protection; on-line setting; mathematical model; set the value; loss function; stochastic gradient; optimal regularization

0 引言

随着电网规模的不断扩大，主网继电结构变得更加复杂，对于主网继电保护进行整定是极为必要的。首先，整定继电保护是为了确保设备的安全运行。电气设计的理论值与设备的实际运行值之间可能存在客观偏差［1］。如果这个偏差超出预定的范围，那么继电保护设备就会触发动作，从而有效地保护人身安全和设备安全。其次，电网中的不同回路或负载的保护动作电流是不同的，需要根据特定的负载选定继电器的动作值［2］。例如，一个具有特定调节范围的继电器需要在电流达到某一特定值时触发，需要对这个继电器的动作值进行相应的调整。最后，对于特定的继电器类型，如电磁继电器，其吸合电流值通常要大于返回电流值［3］，这是由于吸合前的磁路气隙大于吸合后的气隙所导致的滞环（也称为回差）。因此，整定继电器的动作值可以确保设备在出现异常情况时能够及时且准确地作出反应，从而避免设备损坏或安全事故。总的来说，对主网继电保护进行整定不仅可以提高电力系统的稳定性，还可以降低设备损坏的风险，保护人身安全，从而确保电力系统的正常运行。多吉次仁等［4］提出的含双回线路并列运行的110 kV电网继电保护整定计算方案探讨，详细研究了电网继电保护整定计算的运行方式选择、主要整定计算原则及各种典型故障，并探讨了整定计算过程中可能出现的各种问题。但整定计算涉及大量的参数和运行数据，需要耗费大量的时间和资源。徐宇等［5］提出的基于改进海鸥算法的新能源接入配电网继电保护定值优化方法，分析了新能源接入后对继电保护的影响，以分布式新能源接入后的保护灵敏性、速动性、可靠性为约束条件，构建了定值优化模型。但算法中涉及的参数选择会影响算法的性能和收敛效果。综上所述，本研究提出了基于卷积神经网络的主网继电保护在线整定方法，并开展了对比测试，分析验证了该方法的应用效果。

1 主网继电保护在线整定方法设计

1.1 主网继电保护在线整定数学模型构建

对于主网继电保护而言，在对其进行在线整定处理时，需要计算的参数涉及多个方面，对应每种保护类型需要兼顾的整定原则也具有多样化的属性特征。为了能够适应这一特点，需要为每种整定原则构建多个整定公式以满足对应的需求，而在每个整定公式中，又包含多个差异化的定值变量参数［6-7］。结合上述的分析，本研究将主网中的同种保护功能涉及定值变量作为一个集合，并构建主网继电保护在线整定数学模型［8］，具体见式（1）。

[Rv=f（K， X， Y， Z）] （1）

式中：[Rv]为主网继电保护在线整定数学模型；[K]为主网继电保护的电气设备参数涉及定值变量集合；[X]为主网继电保护的故障信息涉及定值变量集合；[Y]为主网继电保护整定规则中涉及定值变量集合；[Z]为主网继电保护整定阶段除上述参数之外的定值变量集合。

结合式（1），对主网继电保护在线整定数学模型涉及的4个数据集合构成的具体信息进行分析，见表1。

按照上述所示的方式，实现对复杂整定规则下具体变量信息的全覆盖，确保在后续的主网继电保护在线整定阶段［9］，处于离散状态的非连续变量可以完整地映射到系统中，使得保护定值能够结合故障信息发生的变化作出适应性调整。

1.2 基于卷积神经网络的主网继电保护定值设置

结合构建的主网继电保护在线整定数学模型，本研究在开展具体的主网继电保护定值设置阶段，引入卷积神经网络，借助卷积神经网络在主网故障特征提取方面的优势，为继电保护定值的设置提供可靠的数据支撑。

首先，将主网历史故障数据（故障类型、故障位置、故障时间、故障电流、故障电压等信息）作为卷积神经网络的输入参数。考虑到构建的主网继电保护在线整定数学模型中涉及变量较多，本研究采用的卷积神经网络架构为ResNet。在卷积处理阶段，选择更加适配于时间序列数据的一维卷积方式，对输入参数的特征进行提取，具体见式（2）。

[g（X）=i=1nZk⊕f（Y）xi] （2）

式中：[g（X）]为一维卷积对主网历史故障数据特征的提取结果；[xi]为具体的主网历史故障数据参数；[Zk]和[f（Y）]分别为[xi]主网历史故障数据状态下对应的其余定值变量参数和整定规则涉及定值变量参数；[⊕]为卷积计算。

在此基础上，将主网继电保护的电气设备参数与正常状态一致程度最高的继电保护定值，作为当前故障的最优主网继电保护整定结果，并通过全连接层将其映射到输出空间中。按照上述方式，可以得到一个映射集。对于实际的主网继电保护定值设置而言，可以将实际的、具体的故障信息输入到卷积神经网络中，利用损失函数计算在随机梯度下降机制下，最优正则化继电保护定值即可，具体计算见式（3）。

[ξ=min（Zk-1λ）Rv*f（Y）xi] （3）

式中：[ξ]为随机梯度下降机制下，满足最优正则化的继电保护损失函数；[λ]为主网继电保护定值整定模型的损耗系数。

按照上述方式，实现对主网继电保护定值的设置，最大限度保障主网运行的稳定性。

2 测试与分析

2.1 测试环境

在分析本研究设计的主网继电保护在线整定方法的应用效果时，以某HT250 配电网环境为基础开展对比测试。对测试环境的基础配置情况进行分析，其中，测试HT250 配电网服务对象为一个中型城市，主要任务是承担居民、商业和工业用户的供电。在运行模式上，测试HT250 配电网采用“环网结构+开闭所”分散供电方式，对应的供电具有较高的可靠性和灵活性。具体运行阶段的额定电压为10 kV，频率为50 Hz。在此基础上，对测试HT250 配电网的继电保护配置情况进行分析。

在线路保护方面，每条10 kV线路均配置过电流保护、方向保护和零序保护。过电流保护定值为最大负载电流的1.3倍，对应的方向保护角度为45 °，零序保护定值为线路电容电流的1.8倍。在变压器保护方面，每台变压器均配置差动保护、过负荷保护和温度保护。具体的差动保护定值根据变压器的额定容量和短路阻抗适应性进行设置，过负荷保护定值则为变压器额定电流的1.2倍。在母线保护方面，采用备自投装置实现母线失电时的自动切换，具体的备自投延时时间设定为0.8 s，执行切换的条件为母线电压低于额定电压的60 %，且持续时间超过0.2 s。

以上述的HT250 配电网继电保护配置和参数信息为基础，开展具体的整定效果分析。分别设置文献［4］提出的含双回线路并列运行的110 kV电网继电保护整定计算方案和文献［5］提出的基于改进海鸥算法的新能源接入配电网继电保护定值优化方法作为测试的对照组。

2.2 测试结果

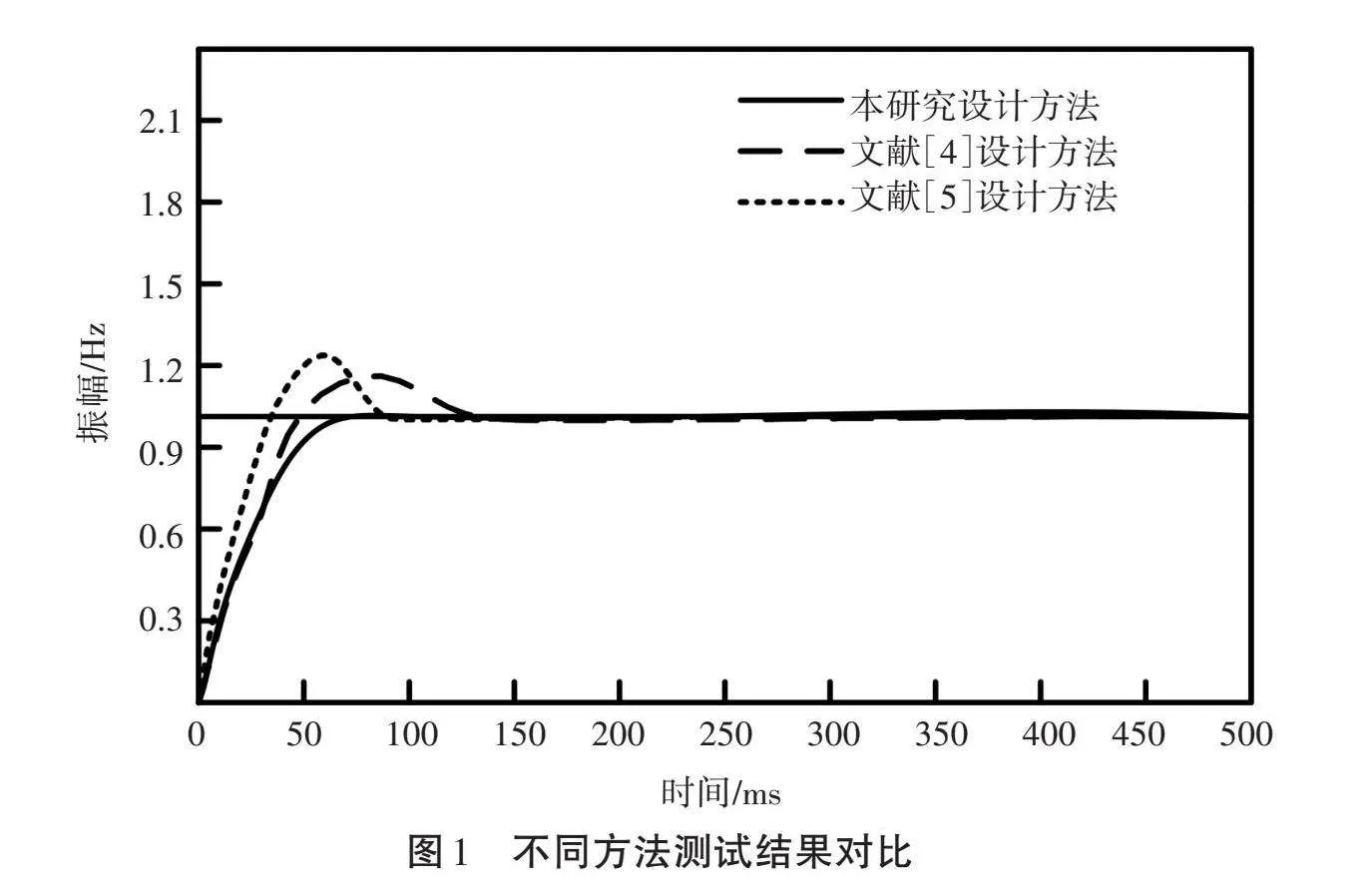
在对具体的测试结果进行分析时，本研究以测试HT250 配电网继电保护在闭环阶跃响应方面的振幅作为具体的评价指标，得到的测试结果如图1所示。

由图1可知，在3种不同的继电保护整定方法测试下，HT250 配电网继电保护在闭环阶跃响应方面的振幅表现出不同的发展趋势。其中，在文献［4］提出的含双回线路并列运行的110 kV电网继电保护整定计算方案下，振幅达到稳定收敛的时间较长，达到180.0 ms；在文献［5］提出的基于改进海鸥算法的新能源接入配电网继电保护定值优化方法下，振幅的过拟合程度较大，最大振幅达到1.40 Hz；在本研究所提出的方法下，闭环阶跃响应振幅不仅在50 s以内实现快速收敛，且对应的振幅相对于对照组而言更加平稳。综合上述测试结果可知，本研究所提出的继电保护在线整定方法具有良好的实际应用效果。

3 结论

本研究提出的基于卷积神经网络的主网继电保护在线整定方法，借助卷积神经网络能够自动地从大量的数据中学习和提取特征的技术优势，实现对不同类型故障和不同系统条件的针对性处理，表现出较强的泛化能力。结合系统故障的潜在规律和模式，能够保障配电网继电保护在闭环阶跃响应方面的收敛性和可靠性。同时，希望本研究能够为提高电力系统的安全性和稳定性提供有价值的参考。

参考文献：

［1］王洋，张永伍，杨畅，等. 基于量子遗传分析架构的分布式电网继电保护定值优化方法［J］. 制造业自动化，2023，45（7）：184-188.

［2］何有良，韦金国，余仕丹，等. 基于Simulink的变压器变斜率比率制动式差动保护仿真校核［J］. 红水河，2023，42（6）：96-101.

［3］马显映，刘小状，陈小松. 电流互感器磁饱和特性对继电保护的影响及防范［J］. 电工技术， 2023 （22）：190-192.

［4］多吉次仁，郝兴宏，蒋双全，等. 含双回线路并列运行的110kV电网继电保护整定计算方案探讨［J］. 大众用电，2023，38（11）：36-37.

［5］徐宇，杨鹏杰，李磊. 基于改进海鸥算法的新能源接入配电网继电保护定值优化方法［J］. 电工技术，2023（21）： 36-41.

［6］廖清阳，陈晓，王军，等. 基于改进花授粉算法的配网继电保护整定优化方法［J］. 粘接， 2023， 50（9）：183-186.

［7］程秀芝，程军，关付生，等. 基于距离保护的输电线路继电保护设计研究［J］. 能源技术与管理，2023，48（5）： 36-38，55.

［8］黄磊，李梅. 基于CSM的含DG配电网自适应过电流保护优化整定计算［J］. 兰州工业学院学报，2023，30（5）：54-60.

［9］霍耀佳，孙帆，马莉，等. 考虑分布电容影响的煤矿供电系统漏电故障分析及定值整定［J］. 宁夏电力，2023 （5）：58-65.