基于学生理解的小学数学计算教学研究

【摘要】当前小学数学计算教学存在四个问题：重法轻理、理法不分、理法不融和前后不关联.要有效解决这些问题，教师需要依据新课标理念和理解计算课的“关联性”“直观性”和“申辩性”三个特征，提出相应的解决策略.文章运用听课调研、课例研究、文献研究等方法，提出厚实经历、找准关联点、用好主题图和学会提炼四个解决问题的途径，以强化教师关注学生对算理的理解，促进学生认知结构化，提升学生运算能力和数学思维.

【关键词】感悟；迁移；理解；结构化

引 言

小学教学计算教学对学生今后的数学学习有着重要意义.为了解小学计算教学现状，笔者坚持多年深入课堂，大量听课，通过总结，发现许多教师在上计算课时，普遍表现出重法轻理、理法不分、理法不融和前后不关联等问题，严重制约课堂教学质量的提升.为有效提升小学计算教学质量，夯实学生数学学习基础，我们需要研究探索有效解决问题的办法，以帮助教师通过计算教学，让学生在感悟中建模，在迁移中掌握算法，在直观中理解算理，在对比中发展结构化思维，提升学生的运算能力和数学思维.

一、当前小学数学计算课堂存在的一些问题

（一）重法轻理

《义务教育数学课程标准（2022年版）》下面简称《新课标》中核心素养主要表现之一运算能力的内涵中指出：能够通过运算数学推理能力的发展.在计算教学中，要落实运算能力的核心素养不仅是让学生学会按照计算法则进行计算，还要让学生在理解算理的过程发展数学推理能力.所以算法如不是建立在对算理的理解之上，那么算法就是无源之水，学生的学习只是机械的操作，谈不上有意义的建构.

如在教学除数是一位数的除法时，教师只是让学生按照教师教学的方法去进行计算，但是为什么除法竖式与加、减、乘不一样呢？教师没有讲到，还有商为什么写在十位或是个位呢？也没有讲，只是告诉学生被除数前面一位数学不够除所以要看前两位，所以商要写在十位上，学生只需要按照教师所讲的方法进行计算就可以了.

这种机械操作，讲练结合的教学方式造成学生对于计算只知其一，不知其二.由于对算理没有理解，学生就不会有认知的迁移，到了除数是两位数除法时，教师又得重新再教学一次.这样的教学严重制约了学生思维的发展，不利于学生的可持续学习的发展.

（二）理法不分

算法即计算的具体操作方法，而算理则是操作的理由，也就是解释操作的合理性.但是在很多时候教师在教学的过程中却出现了法理不分的现象，错把算理当成算法.

如在教学“整十、整百、整千数乘一位数”口算的这节课中，教师出示20×3，让学生自主探究如何计算时，

生1：先用2乘3得6，再在6的后面添1个0.

生2：用2个十乘3得6个十，即60.

师对两种方法都做了肯定，并说：“这两种方法都可以算出结果”.

其实，生2所说的其实是生1的算理，也就是解释为什么用2乘3得到的结果要添1个0，而不是添2个0，所以生1说的是算法，生2说的是算理.显然教师在备课时理法不分，错把算理当算法来教.

（三）理法不融

《新课标》指出：运算能力主要是指“……理解算法和算理之间的关系.”但是在计算教学中，理法不融的现象还是普遍存在的.

如在“两位数乘一位数不进位”一课时教学中，教师出示12×3，并要求学生用自己的方法解决.学生有的用连加的方法：12+12+12=36，有的用分组算法：10×3=30，2×3=6，30+6=36，也有学生用竖式计算法：

教师让这三名学生分别展示之后，直接告诉学生，前面我们已经学习了用加法和口算方法计算，今天我们就一起来学习竖式计算.接着让学生说一说，积中的6是怎样算出来的，3是怎样算出来.然后让学生按照这样的方法进行计算.

口算与竖式计算有着密切的联系，竖式计算的每一步都是有相应的口算，只有教师把口算与竖式计算联系起来，融合为一体，学生才能明白积的每一位表示的意义，才能理解竖式计算，而不是机械操作.

（四）前后不关联

在小学数学教材编排中，知识之间存在内部逻辑，也正是这个内在的逻辑构建了整个课程的体系，因此知识之间有着千丝万缕的联系.《新课标》在课程实施中指出：了解数学知识的产生与来源、结构与关联、价值与意义…….在数学教学中要重视学生的前知识，重视新旧知识的关联，帮助学生把未知转化为已知，自主建构个人知识体系.

可是在课堂中常看到，一些教师在教学中仅着眼当前，没有关注学生眼脱肛所学知识，没有关注新知与旧知的关联点，开展的是碎片式的教学.

如在教学“多位数乘两位数”时，教师可以把这个内容当成一个全新的内容来教学，忽略了学生原来所学过的多位数乘一位数的算法及算理，教学还是按原来方法一样，这样的教学学生失去了，迁移旧知理解新知，自主建构的过程，使学生所学之知识碎片化，零散而没有结构，这样不利于学生对知识的理解及掌握，更不利于形成化未知为已知的思维培养.

二、理解的计算课的特征

理解，即“学习就是理解，理解就是一个意义赋予的过程，即学生必须依据自己已有的知识或经验对建构的对象做出解释，在新的学习材料与主体已有的知识和经验之间建立起实质性的联系，从而获得真正的意义的认知.理解的计算课一般体现以下三个方面的特征.

（一）关联性

关联指新旧知识之间的关联，算理与算法融合，让学生在旧知迁移过程中自主建构知识.如前面所讲的多位数乘两位数的教学是建立在多位数乘一位数的算理及算法的基础上的，因此，理解的计算教学是，教师利用学生原有知识，找到原有知识与新知识的关联点，做好充分的铺垫，让学生跳一跳就可以摘到苹果.

（二）直观性

数学的抽象特性决定着学习数学的困难，因此，理解的计算教学强调通过直观来帮助学生理解符号的推算.

（三）申辩性

申辩是一种深度学习的行为，通过申辩可以加深人们对问题的认识，同时在申辩的过程中，通过倾听别人的观点，可以拓展一个人对问题的全面理解，也是对学生数学思维及数学语言的培养，能促进学生学会有理有据地表达能力的培养.理解的计算教学提倡学生之间的申辩，注重给学生创设可申辩的课堂氛围和申辩的问题.

三、实施理解性计算教学的方法

理解性计算教学是在教学中以学生的原有认知为基础，力求让学生在经历探索算理和算法的过程中，进行有意义的迁移，帮助学生在建立新旧知识联系中，实现学生对知识的自主建构.

（一）厚实经历，在感悟中建模

《新课标》在原来的“双基”的基础上提出了“四基”.四基是指：基础知识、基本技能、基本活动经验、基本思想.只有丰富的经历，学生才能在领悟中理解算理，掌握算法，感悟其数学思想.因此在新课标引领下要重视学生的学习过程，让学生充分地经历探究，特别是计算教学更要注重学生感悟的过程，这样学生才能在掌握算法的过程中感悟数学思想方法，培养学生的数学眼光和数学思维，发展学生的核心素养.

如在教学“两位数乘一位数”一课中，教师让学生通过动手操作理解了竖式与横式所表示的意义，理解了竖式的计算方法及其中的道理之后，教师并没有直接告诉学生最简单的竖式书写方法，而是让学生按照最原始的竖式书写方法计算6道练习题.学生算完了之后，教师引导学生观察、思考，提问：“你对这些算式的书写有什么想说的吗？”通过教师的提问，学生认真观察6个算式，有一个同学发现，其实第二步算出的几十可以直接写在第一步结果的十位上，这样整个算式书写起来就简便多了，经这位同学提醒，其他的同学也发现了.

正所谓山重水复疑无路，柳暗花明又一村.教师并没有把最优的方法直接告诉学生，而是让学生在计算的过程中经历观察、思考、交流、发现、总结出来，在解决问题中感悟，在感悟中建模，发展学生的核心素养.

（二）找准关联点，在迁移中掌握算法

数学教学活动必须建立在学生的认知发展水平和已有知识经验基础之上.特级教师曹培英在《跨越断层，走出误区：“数学课程标准”核心词的解读与实践研究》一书中说：新授课前的复习、铺垫而言，它的初衷：一是为了通过再现或再认识等方式激活学生头脑中已有的相关知识；二是作为新授的过渡或分散新授的难点.

小学数学教材的编排，知识是呈现螺旋上升趋势的，前面的知识往往是后面知识的基础，知识之间存在着密切的联系，特别是计算教学内容的编排就更为明显，所以理解的计算教学要找到知识的连接点，做好铺垫，让学生实现知识的迁移，让学生在迁移的过程中理解算理掌握算法.

如在教学“20以内进位加法”时，教师复习、铺垫的有效性非常突出.其中最关键的铺垫是：口算9+1+1，9+1+2，9+1+5……

教师：为什么你们算得这么快？学生：因为前面都是9+1，正好凑成十.

然后接着让学生口算9+2，9+3，9+5……

教师：为什么你们还是算得这么快？根据学生的回答，教师板书：

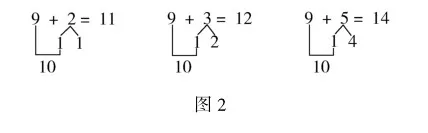
接下来，让学生独立口算8+3，8+4，8+6……小组交流自己是怎么算的……就这样，学生拾级而上，很快领悟了凑十的算法.

凑十法的教学是建立在10加几基础上进行教学的，在这节课中教师抓准新旧知识的关联点，没有直接讲什么是“凑十法”，而是让学生经历对比计算，利用前面的学习经验和口算基础进行引导，学生从看到到想到，实现知识迁移，理解“凑十法”.

（三）用好主题图，在直观中理解算理

《新课标》提出要培养学生“三会”，即用数学的眼光观察现实世界，用数学的思维思考现实世界，用数学的语言表达现实世界.“三会”能力的培养与现实世界都有关.因此，在教学中教师要善于利用和创设有意义的情境，让学生在生活情境中发现、提炼数学问题，培养学生的数学眼光.

教材在每个单元中都会有一个主题图，专家们对主题图的选取并非单一，而是内涵丰富，主题图能把问题置于情景中，让学生在经历情景中抽象出数学信息，直观理解算法，建构数学模型，发展数学的眼光和数学的思维.

如在教学“乘法分配律”一课中，教师出示主题图，如图3，并在主题图旁边出示文字表述：一共有6个小组，每个小组里4人负责挖坑、种树，2人负责抬水、浇树.一共有多少名同学参加这次植树活动？

教师让学生先读一读题，接着问：“这小段话都告诉了我们什么数学信息吗？”

生：一共6个小组，每小组4人负责挖坑、种树，2人负责抬水、浇树，要求一共多少人参加植树.

师：认真观察主题图，你能从图中找到相对应的量的并圈出来吗？

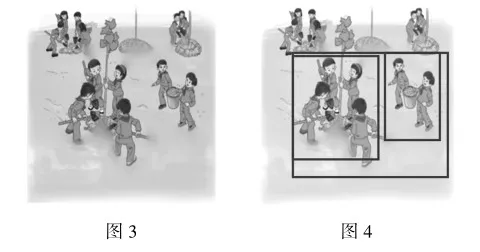
通过教师的提问引导，学生对照主题图找到相应的量，根据学生的回答，教师在图中圈出相对应的量，如图4.接下来，教师让学生根据圈出来的量列出不同的算式来解决这个问题.最后教师让学生对照主题图汇报列式的道理，使学生明白乘法分配律及其互逆关系.

利用主题图，让学生在观察主题图的过程中，培养学生发现信息及对信息加工处理的能力，让学生在处理信息的过程中算理直观化，培养学生数学的眼光.通过主题图的圈一圈，让学生把文字表述与主题图建立联系，帮助学生更好地理解数量关系，使学生自觉把主题图与乘法意义结合起来直观理解乘法分配律的算理.

（四）学会提炼，在对比中发展结构化思维.

特级教师蔡圣宏说：“之所以死记硬背，那是因为不理解”.建构主义哲学认为：学习就是一种用旧知识建构新知识的过程.小学数学计算的法则较多，如果机械记忆只能消耗学生更多的能量，所以要提高计算教学效果，教师需要帮助学生建构知识体系，使知识结构化，才能达到提质减负增效.

通过初步的理解，再到异分母分数的加减法，最后到找共同点，这样分步比较，分步提炼，抓住加减法的本质，帮助学生自主把分数加减法和原来的整数、小数加减法知识建立联系，把分数加减法知识纳入原来加减法的知识体系，形成知识结构，提升了学生的认识水平和认识维度.

结 语

运算能力是数学学习的核心能力，也是数学学习的基础，但是计算并不等同于技能，更是思维能力的培养，因此，新课标视域引领下的计算教学中，教师要注重学生对知识的理解，强化知识的结构化，才能有效地帮助学生提高运算能力和思维能力.

【参考文献】

[1]孔凡哲曾峥.数学学习心理学（第2版）[M].北京：北京大学出版社，2012.

[2]曹培英著.跨越断层，走出误区：“数学课程标准”核心词的解读与实践研究[M].上海：上海教育出版社，2017.

[3]徐戍丹.小学数学计算教学优化策略探微[J].数学学习与研究，2023（30）：62-64.