“面积的测量”的教学探索

【摘 要】学习迁移的必要条件是同时具备共同性与差异性。因此，在《义务教育数学课程标准（2022年版）》中新增“面积的测量”的教学内容。要实现迁移，仅理解面积概念远远不够，还需明确面积测量与长度测量的内在联系与本质区别。然而，当前教学实践普遍侧重两者基于度量单位累加的共性，而对其差异有所忽视。教师应致力于澄清面积测量与长度测量的差异，剖析忽视此差异导致的学习困难，并通过“知一求二”的课堂实践，在学习目标、学习任务以及评价方式等方面进行面积测量教学的探索。

【关键词】概念转变；长度测量；面积测量；度量单位

《义务教育数学课程标准（2022年版）》（以下简称“2022年版课标”）在第二学段课程目标中强调，学生的数学学习应“经历平面图形的周长和面积的测量过程”。与《义务教育数学课程标准（2011年版）》中要求学生“经历用不同方式测量物体长度的过程”相比较，在2022年版课标中新增了“面积的测量”的教学内容。这一变化反映了数学教育对度量本质（即单位累加）的重视，可以促进学习迁移。在讨论学习迁移时，瑞典教育家马飞龙（Ference Marton）在其变异理论中指出：“共同性与差异性同等重要，没有共同性不会有迁移，但是没有差异性也不会有迁移。”［1］因此，要实现迁移，仅关注知识间的共性是不够的，还必须重视其差异性。换言之，“意义源于差异，差异始于比较”［2］。那么，对面积测量和长度测量进行比较，它们之间究竟存在哪些差异？如果忽略这些差异，学生在学习中会遇到哪些学习困难？如何通过教学来探索彰显面积测量与长度测量之间的差异？这样的教学探索蕴含着怎样的教育价值？

一、面积测量与长度测量的差异

什么是测量？17世纪，德国著名哲学家、数学家莱布尼茨（Gottfried Wilhelm Leibniz，1646—1716）指出：“测量是被测物与单位（Unit）的比较（Comparison）。”［3］一旦度量单位得以明确，即确立了“一”的概念，测量过程就是“知一求几”的过程。这一过程的核心在于对连续量进行细分。当一个适当的度量单位被选定后，连续量被分解为离散状态，通过度量单位的选择、确定及迭代，原本难以计数的连续量转化为可计数的离散量。通过“知一求几”，连续量不仅被赋予了具体的数值，还在量与数之间建立了联系，从而“实现了数与量之间一一对应的关系”［4］。在面积测量与长度测量中，尽管它们都遵循度量单位迭代这一基本原则，体现了测量的共性，但两者之间也存在着明显的差异。

测量是用数表达量的过程，其核心在于与度量单位的比较。在长度测量中，具体化为长度单位与被测物的比较。以厘米为单位测量长度为例，首先确立厘米作为度量单位，然后通过该单位的重复累加，直至覆盖被测长度，从而得出以厘米为单位的测量结果。这一过程可以理解为多个厘米单位的线性排列或累加。例如，测量一条2厘米线段的长度，先确定的是长度单位1厘米，再用它重复2次，就得到2厘米的长度（如图1）。从直观上看，2厘米的长度即为两个1厘米长度的累加。无论这个图形如何绘制，只要是2厘米长度，其呈现出来的形状都是一样的。这体现了长度测量的一个显著特点“量等形同”。简而言之，长度测量确保了等长线段在二维空间中的表现形式具有唯一性。

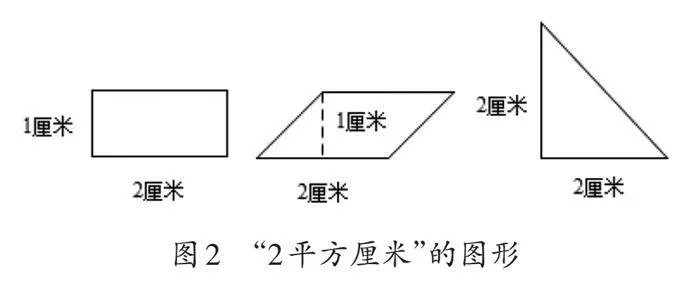
在进行面积测量时，若以平方厘米作为度量单位，有一个显著的特点：即使两个图形的面积相等，它们的形状亦可呈现多样性。例如，一个面积为2平方厘米的图形，可以是长为2厘米、宽为[1]厘米的长方形，也可以是底为2厘米、高为[1]厘米的平行四边形，还可以是一个底为2厘米、高为2厘米的三角形（如图2）。这种多样性揭示了面积测量的一个独特现象：即便图形面积等量，其外在形状也并不唯一。可将这种现象称为“量等形异”。因此，面积测量与长度测量之间的一个明显差异就是：前者允许在面积相等的情况下体现形状的不确定性，而后者则严格遵守等量必同形的规则。

在探讨长度和面积的测量时，会展现出两者的本质区别。长度测量涉及被测物和度量单位之间的线性关系，即单位长度的重复累加，呈现出“同倍增减”的特征。相比之下，面积测量则涉及一维和二维之间的关系，即边长与面积之间的关系。这种关系超越了简单的线性“同倍增减”，转而表现为“此起彼增”的协变关系，即边长增加或减少会导致面积以非线性的方式相应增加或减少。显然，面积为2倍关系的两个正方形，其边长之间并非简单的线性比例关系，而是涉及无理数的概念，这进一步凸显了面积测量的独特性和复杂性。因此，面积测量和长度测量的第二个明显差异就是：前者涉及面积和边长之间这种独特的协变关系，而后者没有。在学习过程中，这些明显差异可能导致学生认知上的困难。

二、忽视差异导致的学习困难

在面积测量教学中，若过分强调其与长度测量的一致性，聚焦于度量单位的累加，可能会产生一个常见的误解：正方形的边长扩大2倍时，面积也随之扩大2倍。为了探究这一问题，笔者对北京一所小学的四、五、六年级学生进行了专项测试，这些学生已经学习过“面积”这一概念。测试内容围绕小学数学教科书中“关于1平方厘米的定义”（如图3），旨在通过调查研究了解学生对正方形面积与边长之间关系的理解情况。测试结果表明，这一误解在不同年级中普遍存在，尽管随着年级的升高，误解的比例有所下降，但仍保持在较高的水平：四年级约有80%的学生、五年级约有60%的学生、六年级约有50%的学生持有此类误解。

在已有的研究中，此类误解被称为“线性误解”，即学生倾向于认为一个变量的变化直接导致另一变量等比例变化，表现为当一个物体的某个向度扩大n倍或增加n，另一个向度也会被认为扩大n倍或增加n［5］。这样的误解普遍存在。例如，在三年级学习了面积单位后，学生被问及边长为1厘米的正方形面积是1平方厘米，用符号表示为1 cm2，那么边长为2厘米的正方形面积，用符号应如何表示？约有66%的五年级学生和30%的六年级学生错误地写成2 cm2，这进一步印证了学生在理解面积与边长的协变关系上存在线性误解。

分析线性误解产生的原因，不难发现，学生受到已有经验中“同倍增减”线性关系（如“1双袜子2只，2双袜子4只”）的影响。瑞士心理学家皮亚杰（Jean Piaget，1896—1980）对儿童面积概念认知规律的研究也证实了这一观点，当正方形的边长扩大为原来的2倍时，儿童会对面积变为4倍感到惊讶，但无法解释为什么，原因是他们的认知水平仍停留在“线性测量”上［6］。

综上所述，面积测量教学不能仅关注其与长度测量基于单位累加的共性，还应重视二者之间的差异。正如变异理论所揭示的，对任何事物的理解都不能脱离其与其他事物的相互联系。人们之所以能够辨识某一事物的特征，是因为这些特征在与其他事物的比较中，凸显出差异。迁移的发生正是这种差异性与共同性交织作用、共同推动的结果。也就是说，在面积测量的教学中，不仅要将长度测量作为度量单位累加的核心概念进行迁移，还要对长度测量和面积测量的差异进行区分，而后者正是本研究强调的重点。已有研究表明，“关注面积测量和长度测量的差异，要对面积测量中‘知一求二’（即使用面积为1平方厘米的正方形构造出2平方厘米的正方形）的探究活动给予足够的重视”［7］。因此，面积测量教学一个重要的目标是促使学生的认知从线性关系向非线性关系转变，对长度测量经验进行改变、拓展与提升，实现思维中的“概念转变”。那么，如何在教学中实现这一目标呢？

三、“从否认到确认”的面积测量教学

在对已有经验进行改变的过程中，先要感知已有经验的不足，并对其加以否认。在学习面积测量之前，学生所积累的长度测量经验包括“度量单位的累加、量等形同以及线性关系”等。如果未能对这些经验进行适当的区分，直接迁移到面积测量学习中，就会产生一些理解上的偏差，从而阻碍新知的学习。因此，学生要正确理解面积测量中边长与面积的协变关系，必须对在长度测量中积累的线性经验进行否认，这是概念转变的第一步。

实现概念转变，不仅需要掌握“是什么”和“为什么是”的学科逻辑，还应具备“如何知道并相信”的认知逻辑，即一种“从否认到确认”［8］的认知过程，可以分解为“枚举—否认—承认—确认”的基本认知框架（如图4）。

首先，基于学生已有经验枚举出“可能是什么”；其次，通过比较和筛选多种可能性，排除“不可能是什么”，从而产生“不能这样做，可以怎样做”的想法；接着，在筛选的基础上，承认“可以这样做”并进一步形成“应当是什么”的想法；最后，在承认的基础上，进一步证实“应当这样做”，并坚信“一定是什么”。这一认知过程遵循“先识其非，方知其是”的思维路径，强调了否认作为承认与确认的先决条件，意味着要对“是什么”进行认定，必须先经历对“不是什么”的辨析与排除。

这种“从否认到确认”的认知方式，可以广泛应用于小学数学课程教学中，特别是在需要进行概念转变的教学实践中。在面积测量中认识“协变关系”时，学生应在承认和确认面积测量“是协变关系”的同时，也明确其“不是线性关系”，即予以否认。同理，对“为什么是协变关系”的解释和对“为什么不是协变关系”的解读也应共存并相互支持。只有在排除了“不是协变关系”的可能性之后，才能真正相信并确定“是协变关系”以及“为什么是协变关系”。以下，将以面积测量中“知一求二”的学习任务设计与实施为例进行说明。

●任务一：已知边长1分米的正方形面积为1平方分米，画一个面积为2平方分米的正方形。

实践研究表明，学生受长度测量经验中线性关系的影响，全班35名学生出现了以下三种尝试（如图5）：边长为2分米的正方形（约占85.71%），边长为1.5分米的正方形（约占8.57%），长为2分米、宽为1分米的长方形（约占5.72%）。值得注意的是，这些学生在初始阶段均未意识到自己的错误。如何引导学生对这些想法进行否认呢？

在教学中，教师引导学生围绕核心问题“这幅作品是否为2平方分米的正方形？请说明理由”展开讨论，学生逐渐认识到：边长为2分米的正方形面积过大，边长为1.5分米的正方形面积不够精确，长为2分米、宽为1分米的长方形在形状上不符合。这一共识的达成，标志着学生开始意识到他们无法直接通过长度测量的方法确定面积。

这一任务不仅是学生概念转变的起点，还是他们认知升级的关键一步。他们开始意识到，在面积测量中，不能简单地将长度测量的经验套用过来，从而感知“不能这样做”，进而想到“应当怎样做”。这样，下一个任务的出现则水到渠成。

●任务二：从任务一的三种作品中，挑选易于改造的作品进行改造，以得到2平方分米的正方形。

学习材料：如图6中情况1和情况2的彩纸，一把剪刀。

如何引导学生认识到“应当怎样做”以达成对面积测量的认同？教师提出核心问题让学生边操作边思考：“我是怎样改造原图，使其变成2平方分米的正方形的？我是怎么想到这个方法的？”在全班交流中，用这个核心问题不断引导学生关注图形与图形之间的关系，从而找到解决问题的办法。

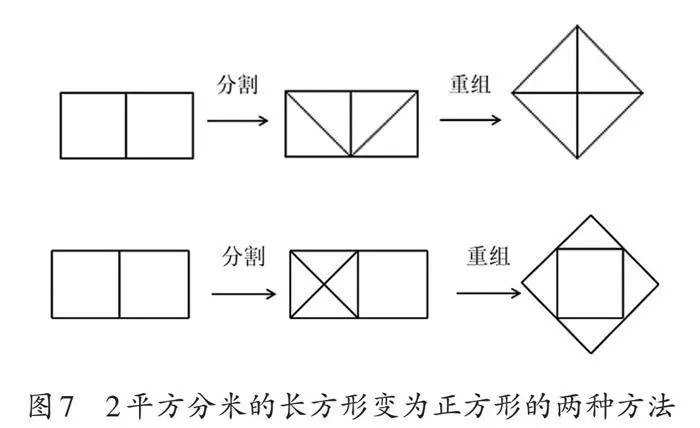
针对情况1，学生展现出非凡的创造力，他们不仅缩小了单位面积，还巧妙地运用了图形的运动。有的将两个正方形进行分割，形成4个面积是0.5平方分米的三角形，再将它们重新组合得到正方形；还有的将一个正方形进行分割，形成4个面积是0.25平方分米的三角形，再进行重组得到正方形（如图7）。

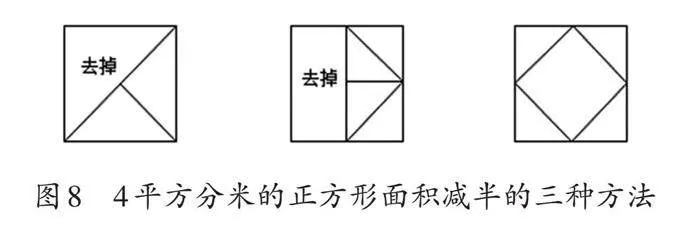
在情况2的处理上，学生同样运用了多样化的方法。其中，两种是先对正方形进行减半，形成面积为2平方分米的三角形或者长方形，随后通过分割与重组，将其转化为正方形；另一种更为直观，通过折叠找到正方形每条边上的中点依次连接，直接构造出面积为2平方分米的正方形（如图8）。

学生观察到图形与图形之间的关系，借助以前学习图形运动的经验，得到了想要的2平方分米的正方形实物，由此体会到“可以这样做”的合理性。但是，画一个2平方分米的正方形，除了每次都这样减半、分割、旋转，还有没有别的办法？由此引出“应当怎样做”的任务。

●任务三：在1平方分米的正方形中找2平方分米正方形的边长，可以画一画，描一描。

教师为了引导学生理解“应当怎样做”，提出了核心问题：“在1平方分米的正方形中，2平方分米正方形的边长如何确定？”实践证明，尽管该任务具有一定的挑战性，但仍有部分学生迅速洞察到其中的关系——1平方分米正方形的对角线长度恰好等于2平方分米正方形的边长（如图9）。这一发现激发了学生“无中生有”的想象力，有助于培养他们数学的眼光。完成此任务不但帮助学生通过图形关系确定了2平方分米正方形的边长，而且为他们后续重新绘制2平方分米正方形提供了有力支持。

●任务四：请你们画一画面积为2平方分米的正方形。

在这个任务中，学生借助前两个任务中积累的经验，提出了多种解决方案。一些学生选择在原有作品的基础上进行改造，通过连接中点等方法得到目标图形；一些学生则采用分割与重组的方法；更有学生直接应用了任务三中的发现，利用1平方分米正方形的对角线作为边长绘制出精确的2平方分米正方形。这一系列操作不仅展示了学生丰富的想象力与创造力，而且彰显了他们在数学学习过程中的成长与进步。

学生的学习活动轨迹，从“初尝失败，反思为何不能如此”到“勇于创新，探寻可行路径”，再到“数学眼光，确定最佳方案”，最终“运用经验，探索更多可能性”。其思维过程也经历了“不能这样做—可以怎样做—应当怎样做—还可以怎样做”的转变。学生逐渐从困惑走向清晰，深入思考，并实现了从长度测量的线性关系到面积测量的协变关系的转变。

四、面积测量教学新探索的价值

在2022年版课标背景下，尽管面积测量中“知一求二”的学习任务并非现行小学数学教科书中明确的教学内容，但在课堂实践中却有其丰富的教学价值。

学习目标定位，从知识掌握转变为素养提升。本次教学探索体现了以素养为导向、以育人为本的教育理念。它超越了传统面积测量教学中单一关注公式推导、记忆应用的模式，转而重视培养学生的数学眼光和量感。通过引导学生对正方形对角线“无中生有”的想象，将面积为4平方分米的正方形沿对角线分割减半，以图形运动的方式转化为2平方分米的正方形。此类活动聚焦于量的本质及其相互关系，淡化了对公式的依赖与计算的强调，可称之为“量推理”［9］，直指量感的形成。此外，变异理论的运用促使学生从线性水平迈向非线性水平，实现了概念转变，促进了数学思维的提升。学生的认知虽然始于已有经验，但不应囿于其中，已有经验的转变、拓展与提升应成为数学课程教学的目标。

学习任务设计，从教师直接告知转变为学生主动探索。本次探索改变了以往教学中将知识直接告知的方式，巧妙设计了富有挑战性的学习任务，利用反常现象激发学生的好奇心与求知欲。例如，在绘制2平方分米正方形时，学生无法直接得出边长，这一困惑成为推动学生深入探索的动力。通过对错误作品的比较、分析与改造，学生直观感知量与量之间的关系，深化对面积测量意义的理解。此外，基于对已有经验差异的理解，让学生从“意义源于差异”的视角，把握长度测量和面积测量的不同，经历从否认到确认的学习过程。在这样的框架下设计学习任务系列，让学生在独立思考、动手实践、自主探索、合作交流中触及新知本质，发生真实的学习，发展核心素养。

评价方式转型，从否定错误到激励成长。在面积测量教学中，摒弃了以往简单否定学生错误的做法，转而将其视为宝贵的教学资源与成长契机。任务一中引导学生通过正视错误、分析错误、反思错误，理解了“不是什么”和“为什么不是”，并转换角度寻找新的解决之道，帮助学生建立正确的错误观与成长观。这种评价方式的转型不仅减轻了学生的心理负担，更激发了他们的探索欲望与创新精神。这种关注过程、激励成长的评价方式正是2022年版课标所倡导的，也是未来教学评价改革的重要方向。

参考文献：

［1］陈建翔．“变异理论”对传统迁移观的超越及启发［J］.中国教育学刊，2009（1）：30-33．

［2］ MARTON F. Necessary conditions of learning［M］. New York：Routledge，2015：48.

［3］ RESCHER N. Leibniz’ conception of quantity，number，and infinity［J］. The philosophical review，1955，64（1）：108-114.

［4］ RUSSELL B. The principles of mathematics［M］. Cambridge：Cambridge University Press，1903：176.

［5］ STAVY R，TIROSH D. How students （mis-）understand science and mathematics ［M］. New York：Teachers College Press，2000：3.

［6］ PIAGET J，INHELDER B，SZEMINSKA A. The child’s conception of geometry［M］. London：Routledge and Kegan Paul，1960：406.

［7］ 郜舒竹，吕港丽. 面积测量中值得重视的“知一求二”［J］. 教学月刊·小学版（数学），2022（10）：4-8.

［8］ 郜舒竹，李娟. 平行四边形的面积：从否认到确认［J］. 教学月刊·小学版（数学），2022（12）：4-8，17.

［9］郜舒竹，罗玉晓. 面积测量与计算中的“眼光”［J］. 教学月刊·小学版（数学），2022（11）：4-8，62.

（1.北京市北京小学丰台万年花城分校

2.首都师范大学初等教育学院）