除数是非整十数的除法：巩固算理，初识算法

【摘 要】以“除数是整十数的除法”为基础，探索一条基于算理一致性，且学生易于理解的“除数是非整十数的除法”的学习路径，以此凸显除法运算的通性通法。通过承接已有知识，引导学生将除数是整十数的除法的算理迁移到除数是非整十数的除法的计算中，感悟除法运算算理的一致性；经历计数单位细分的过程，解决除数是非整十数除法的算法难题。学习路径凸显以理带法，帮助学生通过计数单位的细分，理解算理，掌握算法，提高运算能力。

【关键词】除法；计数单位；单位细分；学习路径

一、问题提出

“除数是非整十数的除法”承接“除数是整十数的除法”的学习内容，与其在算理上具有一致性，均是“计数单位的细分”。但相较于“除数是整十数的除法”，“除数是非整十数的除法”更具有一般性。因此，让学生在“除数是非整十数的除法”的学习中继续经历计数单位细分的过程，有助于凸显除法运算的通性通法。

现行教材中，除数是非整十数的三道除法算式84÷21、430÷62和197÷28，它们的商都是一位数，学生无法充分体会计数单位细分的过程。而且由于除数和被除数间的差距较小，学生通过口算即可得出准确商，也难以体现将除数估成整十数试商的价值。因此，笔者将商是两位数和商是一位数的除法整合在一起进行教学，使学生通过对比深入理解计数单位细分的过程，感悟运算的一致性。

本研究将继续聚焦“计数单位的细分”，以“除数是整十数的除法”为基础，探索一条基于算理一致性，且学生易于理解的“除数是非整十数的除法”的学习路径，以此凸显除法运算的通性通法。研究主要围绕以下两个子问题展开。

（1）如何进一步经历计数单位细分的过程，将“除数是整十数的除法”的算理迁移到“除数是非整十数的除法”的计算中，以凸显除法运算算理的一致性？

（2）如何利用计数单位细分的过程，解决商的位置和商“0”的算法问题？

基于此，笔者选取杭州市YHSY小学四年级两个平行班（分别记为甲班和乙班）共58名学生作为研究对象，按照研究设计的学习路径进行教学。通过比较两个班级学生的学习情况，检验优化后的学习路径的教学效果。学习路径优化的具体流程如图1所示。

二、路径优化

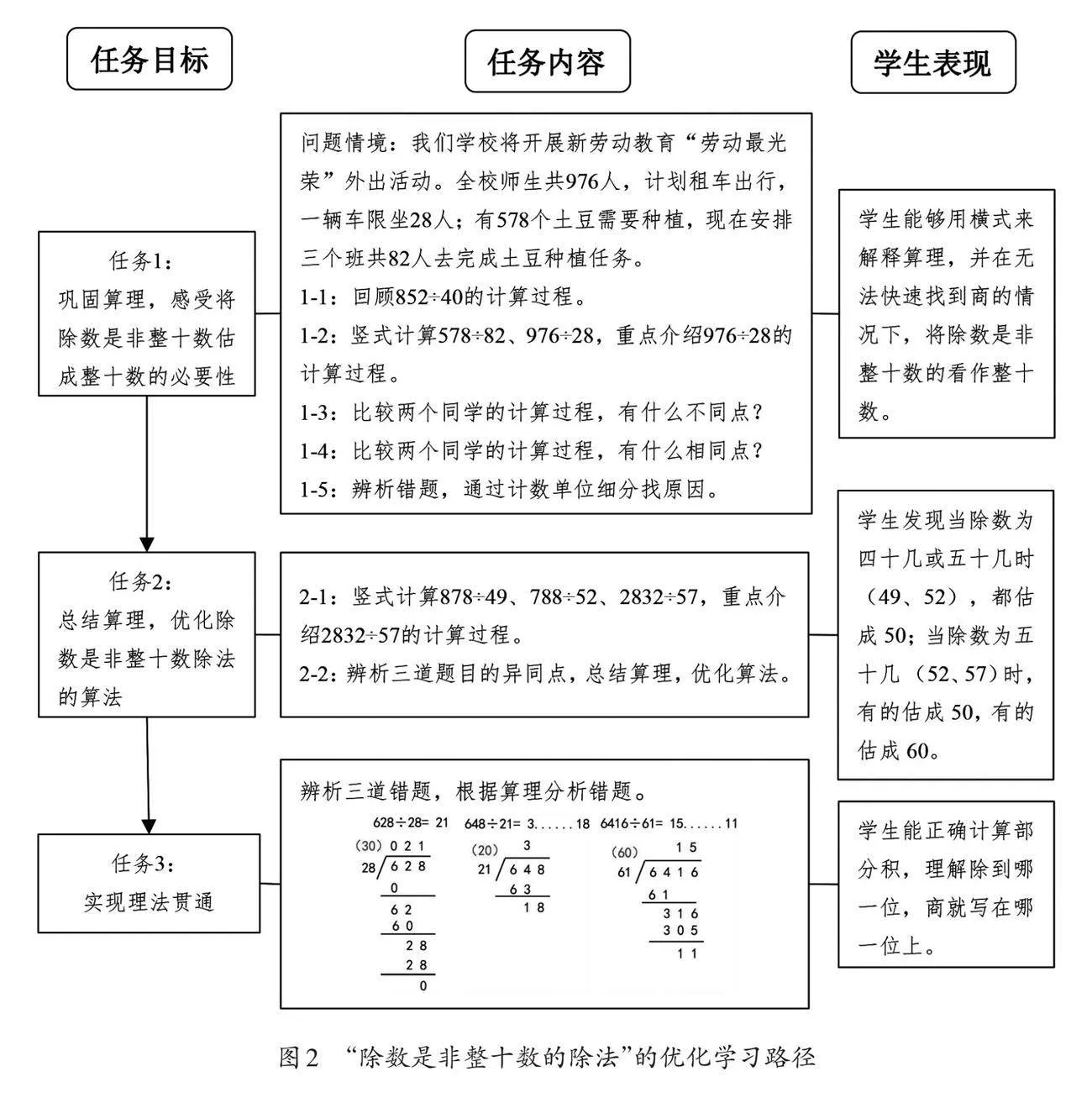
图2是优化后的“除数是非整十数的除法”的学习路径，分三个任务逐步推进教学。首先，任务1借助三道除法算式852÷40、578÷82、976÷28，引导学生回顾“除数是整十数的除法”的运算过程，并将其算理迁移到“除数是非整十数的除法”的计算中，使学生再次经历计数单位细分的过程，贯通除数是整十数的除法和除数是非整十数的除法算理的一致性。其次，基于除法运算的算理，任务2选用三道除数是非整十数且接近50的除法题目，通过异同比较，引导学生感受用四舍五入法将除数估成最接近的整十数最为便捷，能够提高运算效率。最后，任务3围绕三道改错题展开，引导学生以算理解决算法问题，强调所有算法问题均可通过计数单位细分的过程来解决，凸显除法算理的重要性。

（一）承续旧知，贯通算理，从除数是整十数走向除数是非整十数

任务1首先引入除数是整十数的除法算式852÷40，通过计数单位细分的过程，带领学生回顾算理，再由情境自然引出两道除数是非整十数的除法算式578÷82、976÷28，重点讨论976÷28的计算过程，迁移除数是整十数除法的算理。教师在书写竖式的过程中，同时呈现每一步的横式，与竖式一一对应，凸显算理的一致性，即除法就是计数单位细分的过程，均从大的计数单位开始，逐渐分到小的计数单位。板书设计如图3所示。

【教学片段1】

师：同学们，上一节课我们学习了什么？

生：除数是两位数的除法，而且除数都是整十数。

师：那我们来计算一下852÷40。

生：8个百除以40，不够除；85个十除以40等于2个十余5个十，再用52个一除以40等于1个一余12。

师：我们学校将开展新劳动教育“劳动最光荣”活动。仔细观察，你们能提出哪些用除法解决的问题？

生：需要租几辆车？每个人平均要种几个土豆？

师：这两个问题可以用什么方法解决？

生：列除法算式。第一个是578÷82，第二个是976÷28。（教师板书）

师：这两个算式跟我们上节课学的内容有什么不同的地方？

生：上节课我们所学的除法算式中的除数都是整十数，而这节课的除法算式中的除数都是非整十数。

（学生先估算，再进行竖式计算，教师反馈总结976÷28的计算过程）

师：那么这两道题有没有相同的地方？

生：它们都是从高位算起，一位一位往下除的。

师：哪个同学能够帮我们完整地回顾如何计算976÷28？

生：先用百位上的9去除，不够除，百位上商0；再用97个十除以28，把28看成30，得到3个十，十位上商3；最后用136个一除以28，把28看成30，个位上商4，最后余24。

师：请同桌再互相说说578÷82的计算过程。

（二）巩固算理，突破难点，瞄准商的位置

在除数是非整十数的除法竖式的计算过程中，学生往往难以找准商的位置，这是因为他们对除法运算的算理理解不够透彻［1］。因此，在任务1-5中，笔者借助分析商是一位数、商是两位数的除法的错例，让学生再次经历计数单位细分的过程，帮助学生认识到商是几位数并不重要，重要的是瞄准商的位置。

【教学片段2】

（教师出示图4所示的学生错例）

师：请问这个同学遇到了什么问题？

生：他不确定“7”应该放在个位上还是十位上。

师：那应该怎么思考呢，谁来帮帮他？

生：我们可以通过验算来解决。如果把“7”写在十位上，表示“7个十”，70×82就远远大于578，这样算显然是不对的。

生：我认为应该把“7”放在个位上。因为这里是用“578个一”除以82，所以结果应该是“7个一”，而不是“7个十”。

师：大家明白了吗？我们也可以这样理解，当我们计算到十位时，用57个十除以82，不够除，这时如果要商，应该商几？

生：商0。

师：算个位时才够除，所以个位上商“7”。我们一起来回顾一下刚才是怎样计算578÷82的？

生：先用百位上的5去除，不够除，商0；再用57个十除以82，仍不够除，商0；最后用578个一除以82，可以商7，余4。

（三）应用算理，打破壁垒，解密商“0”难题

任务3包含三道改错题，旨在引导学生经历应用计数单位细分的过程，厘清商“0”现象，理解在什么情况下应商“0”。三道改错题通过精心选择设计。第一，选择了一道被除数是四位数且商为三位数的题目（6416÷61），将本内容的算理算法拓展到商是三位数的除法算式中，凸显通性通法。第二，三道除法题目的错误原因各不相同，第一题涉及部分积问题，第二题是商末尾为0，第三题是商中间有0。教师要引导学生发现问题，剖析错误原因并加以修正。例如，在探讨第二道错题时，须着重引导学生理解商3表示“3个十”，再用18个“一”除以21，不够除，因此个位上商“0”。这样，通过计数单位细分的过程，商“0”不再成为难题。

【教学片段3】

（教师出示图5所示的三道错误计算题）

师：请同学们担任小老师，检查一下这三道计算题错在哪里。

生：第一题错在没有使用准确的数来进行计算。这里的“60”是用30乘2得到的，不是准确的数。实际上，应该使用原除数28乘2，等于56余6。

师：我们继续计算下去。计算个位，68个一除以28，可以把28看作30，商2个一，余12。因此结果是22余12。

生：第二题的商的个位少了一个0。因为用18个一除以21，商0余18个一，所以个位上商0，最后结果是30余18。

师：那么最后一道题呢？

生：在计算百位时，64个百除以61，应该商1个百余3个百，但他把这个1写在十位上了。

师：我们一起来计算一下。

生：6个千除以61等于0个千余6个千，64个百除以61等于1个百余3个百，31个十除以61等于0个十余31个十，最后316个一除以61等于5个一余11个一。

师：在计算除数是非整十数的除法时，我们需要注意什么？

生：除到哪一位，商就要写在哪一位上面。即使不够除，也要写0占位。

三、效果检验

为了检验优化后的学习路径的实施效果，本研究设计了三道“除数是非整十数的除法”的后测题（如图6），以评价学生对算理的一致性的理解水平。问卷的Cronbach’s α系数为0.91，表明该问卷具有较高的信度。后测主要从“知识理解、知识迁移、知识创新”三个水平进行检测［2］。各水平任务评分标准如下：学生能运用竖式计算正确，说明达到“知识理解”水平，得1分，回答错误或未作答计0分，评价对象为第（1）题、第（2）题，共2题。学生既能用横式记录笔算过程，又能运用四舍五入法将除数由非整十数转化为整十数进行计算，说明达到“知识迁移”水平，得2分，仅写出横式计1分，计算错误或未作答计0分，评价对象为第（1）题、第（2）题，共2题。学生能将算理算法迁移应用到商是三位数的除法中，且能用横式记录笔算过程并计算正确，说明达到“知识创新”水平，得2分，仅列出竖式计1分，计算错误或未作答计0分，评价对象为第（3）题。

基于此，对甲、乙班的后测结果进行定量分析，得出他们在各水平任务上的平均得分情况（如表1）。从表中数据可以看出，乙班学生有两个水平上的得分率均高于甲班学生，尤其是在“知识迁移”上的表现，两个班级存在显著差异。

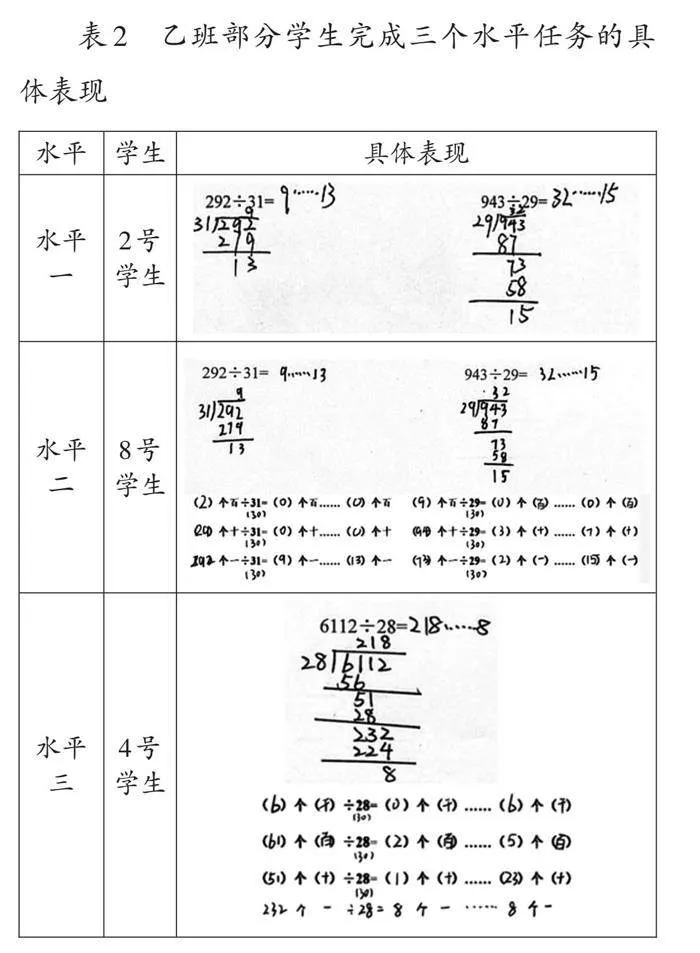
乙班部分学生的问卷答题情况如表2所示。学生能利用竖式计算正确（如2号学生）。他们不仅能用横式记录笔算的过程，还能用四舍五入法将除数由非整十数转化为整十数进行计算（如8号学生）。另有学生能将算理算法迁移应用到商是三位数的除法计算中，用横式记录笔算的过程，又能计算正确（如4号学生）。

由此可见，优化后的“除数是非整十数的除法”的学习路径，在帮助学生打通除数是整十数的除法和除数是非整十数的除法的算理，强化计数单位的细分，理解算理，掌握算法等方面具有较好的效果。

参考文献：

［1］陈雪娇.错误化开 算法自来：“笔算除数是整十数的除法”教学赏析［J］.课程教材教学研究（小教研究），2023（3/4）：76-77.

［2］喻平.《义务教育数学课程标准（2022年版）》学业质量解读及教学思考［J］.课程·教材·教法，2023，43（1）：123-130.

（1.杭州师范大学经亨颐教育学院

2.杭州师范大学中国教育现代化研究院）