以动驭少引题魂 拾级而上筑题阶

摘 要：在注重核心素养的教学理念下，教师的命题理念应当随之改变. 一道题目命制的过程应该是教师进行教学研究的过程，才能让试题实现其应有的价值. 以一道几何压轴题的命制过程为例，简要阐述其命题理念与过程.

关键词：核心素养；正方形；命题；几何

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）09-0051-05

引用格式：周炼. 以动驭少引题魂 拾级而上筑题阶：谈一道几何题的命制与打磨［J］. 中国数学教育（初中版），2024（9）：51-55.

一道好题应该是命题者选取一个熟知度高且包容性广的知识为切入口，将自身视为研究者，用尽可能简约的元素进行沉浸式探索与开发，还能以客观的角度从不同视角进行理性分析，以语言得当、逻辑严密、结构完整的表述形态来呈现，给学生和教师都留有思考的余地和想象的空间. 下面笔者结合自己对好题的理解，简要阐述一道几何题的命制灵感、过程及个人思考.

一、试题呈现

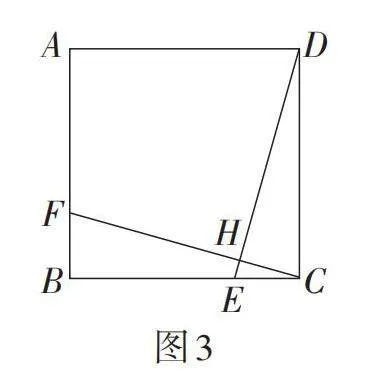
题目 如图1，在正方形ABCD中，点E，F，G分别是边BC，AB，CD上的点，且FG垂直平分DE，交DE于点H，AB = 3.

（1）求证：FG = DE.

（2）如图2，取FG的中点O，连接DO，并作DO的延长线交边AB于点I，连接EI，动点E从点C出发，沿着CB方向由点C向点B运动，到达点B后立刻停止运动.

① 在点E的运动过程中，IB + BE与CG的比值是否会随着点E的运动而变化. 若不变，求出这个定值；若改变，说明理由.

② 求点O运动的路径长.

二、命题的源起、设想与阅卷预设

1. 命题的源起

选择正方形作为命题背景是因为正方形兼具轴对称性与中心对称性，有很大的研究价值与空间，是初中阶段发展学生几何直观、推理能力等数学核心素养的优质素材. 在明确了选题的大方向后，笔者便开始研究教材，在翻阅苏科版《义务教育教科书·数学》八年级下册（以下统称“苏科版教材”）的过程中，第9章“中心对称图形——平行四边形”单元复习巩固中一个类似“十字形”的图形吸引了笔者的注意. 这个图形仅仅是在正方形的基础上添加了两条线段，就能在已知两条线段垂直的位置关系时，通过推理得到两条线段相等的数量关系，反之亦成立. 证明的过程更是将正方形与全等三角形、矩形、余角等图形的性质完美地融合了起来，综合性较强，有较大的挖掘空间. 于是确定以此图形作为命题的基本背景，经过一番研究后，让一个本就不错的几何图形绽放更多的光彩.

2. 命题的设想

选择的图形虽不复杂，但作为一道立足探究、体现素养的几何题，需要考查学生对几何图形的分析理解能力，关注学生探究动态几何问题的方法与策略，以及学生对数学知识之间相互迁移的水平，建构几何与代数之间的联系，用数形结合思想从不同维度思考问题. 由于选材本身已经在正方形的基础上有了一定的拓展，所以在增加条件的过程中所添加线段尽量不超过1 ～ 2条，力求在图形本身的简约性的基础上适当增添一些变量，通过特殊位置的确定赋予其更多的可研究性，并以此作为命题的主线. 否则，当条件过于复杂时，既容易干扰学生的思维，又会让整道题显得杂乱无章，不成体系.

3. 检测目标的设定与阅卷预设

根据要求，本次命题的检测目标是在注重基础知识与基本技能的同时，充分体现学生的数学核心素养水平与综合探究能力. 如此看来，整道题的结构设置应该遵循先易后难、层层递进的原则，让学生先迈出一步，解决一些简单的问题. 随着探究的深入，再逐渐体现学生的能力和素养. 内容的选取要从多个维度出发，确保学生尽可能地发散思维，站在不同的角度看问题，希望在阅卷的过程中能够看到“遍地开花”的方法与策略，在“条条大路通罗马”的命题理念下充分展现学生的核心素养与关键能力.

三、命制与打磨的过程

1. 试题的产生过程

（1）来之不易的两个“一”.

① 基于原题的一条线.

由于题目想以尽可能简约的方式考查学生的探究能力，所以需要让原图的一些元素“动”起来. 于是，尝试将点E设置为线段BC上的动点，其余构成要素不变. 比较有研究价值的是点H在一个圆上运动. 虽然这是一个不错的研究背景，但是这样的构图方式学生已经比较熟悉，缺乏新意. 笔者便想到继续扩大动态因素的运动范围. 试着又增加了一个变量，将点G也设置为线段上的一个动点（如图4）. 但这样设置后，此题中就存在两个主动点，使得学生对探究没有关联的双变量有些摸不着头绪. 最后，决定将变量的运动范围缩小. 经历这样的取舍过程还是有收获的. 在移动FG的过程中，发现可以取一个更特殊的位置来研究问题，即线段DE的中点. 如图5，作DE的垂直平分线交AB，CD于点F，G. 这相较于之前的情况既增加了新意和研究难度，又扩大了动点的运动范围，但相对于完全动点又有所约束，这样的尺度恰到好处.

② 跳出原题的一个点.

有了基本框架后，如何让它焕然一新，成为一道基于教材原题却又不失个性色彩与创造力的新题呢？由于将命题的方向定位于动态几何，所以几何画板软件是一个有力的辅助工具. 在用几何画板软件画出整个图形之后，通过拖动点E，观察其在运动过程中线段之间是否存在不变的关系或者存在有研究价值的问题. 在操作中发现点E在线段BC上从右向左运动时，很多点都在有规律地运动. 例如，点H一直在与边BC平行的水平线上移动，点F，G分别沿着竖直方向向上、向下运动，唯独线段FG的中点位置像过山车一般忽上忽下，这个现象引起了笔者的关注. 由此，取线段FG的中点O，通过几何画板软件的追踪点功能重新将点E从点C到点B再次拖动一遍，结果不出所料，点O经历了先上升（如图6）到达最高处（如图7），随后又下降（如图8）的过程. 由此看来，这个点的运动路径属于“来回型”，既新颖又有研究价值，于是决定以此作为命题的主要研究问题.

（2）数与形的双重表述.

① 以数悟形，直观形象的理性视角.

从几何画板软件的演示过程可以看出点O的运动情况较为复杂，只通过几何画板软件的演示或许可以测量出点O的运动路径长，但对其内在的数学原理及其轨迹的确定并不能解释清楚. 由于涉及该点的条件实在过少，仅从几何角度入手研究并没有太多的思路，于是想到从代数角度入手，从而以点B为原点，BC所在直线为x轴建立平面直角坐标系（如图9）. 设AB = a，CE = x，通过相似、中点公式和函数等知识计算出点O的坐标为[a2， a2-x2+ax2a]. 根据点O的横坐标可以证明点O在直线[x=a2]上移动. 将纵坐标配方为[-12ax-a22+5a8]. 根据二次函数的性质可得，当x从0逐渐增大到a时，点O的纵坐标先由[a2]上升到[5a8]，再由[5a8]下降到[a2]. 那么，在整个过程中，点O运动的路径长为[a4]. 但这仅限于命题者研究问题的一种理性策略，由几何图形研究转向代数建模并非一蹴而就，这中间还有几何画板软件直观层面的引导. 要让初中生用这种方法研究问题几乎不太可能，也不符合学生的认知发展水平，所以还需要寻求更好的命题方式与条件设置，同时需要寻求更好的解题方法.

② 以形托数，聚焦动点的制约关系.

点O是一条动线段的中点，或许从上述代数角度可以通过运算探究其轨迹，但单纯从几何层面来看，点O所处的载体与环境似乎有些“单薄”. 那么，如何才能将研究背景变得充盈、有层次感呢？笔者想到了两种方案. 第一种是过点O作线段BC的垂线，分别交边AD，BC于点M，N（如图10）. 这样暗中提供了点O的运动路径. 同时，点O是点E的从动点，找到了一条能用字母表示且能直接研究路径长的线段ON. 设CE = x，用含x的式子表示线段ON的长，再用二次函数的知识来研究便水到渠成. 然而细想后发现，这样设计给学生直接呈现了轨迹，似乎少了一些探究的乐趣. 于是想到了第二种方案：能否以转化思想为原则将研究点O转化为研究更好操作的点呢？由于点O是线段FG的中点，且AB∥CD，所以联想到可以构造“X型”全等，即延长DO交边AB于点I（如图11），那么点O也是DI的中点，发现点O与点I不仅同属于一个运动层级，而且它们在某一时段内走过的路径长始终构成中位线关系. 于是想到将研究点O转化为研究点I. 连接E，I后，设AB = a，CE = x，根据相似三角形的性质等几何知识可以求得IB =[-1ax-a22+][a4]. 再由二次函数的性质可知IB的最大值为[a4]. 连接BD，取BD的中点[O′]，根据中位线的相关知识不难得出点O的运动路径长为[a4].

（3）探索图形变化中的不变.

一道体现核心素养、综合性强的几何题的命制应该以凸显学生的探究能力、思辨能力及观察能力为导向，立足几何直观、推理能力等数学核心素养，使学生形成合乎逻辑的思维方式和有条理的表达能力. 因此，此时题目虽然有了大致框架，但依然值得通过分析边与边之间的数量关系找到一个变化中不变的结论作为第二个研究话题. 继续利用几何画板软件研究，但这次是站在全局的高度观察图形中的各条线段，发现随着点E的运动很多线段长度都随之改变，这些线段之间一定有值得探索的数量关系，于是决定将研究方向聚焦于此. 要探索这些线段之间的关系，有一条辅助线必不可少，过点G作AB的垂线，交AB于点K（如图12）. 因为CE = FK，而FK与AF，FI，IB共线，所以能够起到通路架桥的作用. 经分析，发现AB = AF + IB + FI，CD = DG + GC，且AB = CD，所以AF + IB = CG，即CG - AF = IB. 由于BK + AF = BE，即CG + AF = BE，将CG - AF = IB与CG + AF = BE两式相加，可得2CG = IB + BE，即[IB+BECG]= 2. 也就是说，无论点E运动到何处，线段IB与线段BE的和恒为线段CG的2倍. 这样的发现可谓意料之外又在情理之中. 意料之外是因为在主问题已经足够精彩的情况下，该图形还能碰撞出这样的火花；情理之中是因为整个图形虽然简约明快，但仅有的几个基本图形之间却严丝合缝，相得益彰.

2. 试题的打磨与优化

（1）首问设置应全盘托底.

首问可以视为一道题的标杆，既是研究的起点，也应渗透研究的方法与策略. 设置好首问既有利于整个问题的连贯性与可研究性，也可以无形之中将学生包含在一个主题明确的思维场域中，以此为中心聚合学生学过的知识与方法解决问题.

原本第（1）小题是这样设置的：在正方形ABCD中，点E，F，G分别是边BC，AB，CD上的点，且FG垂直平分DE，交DE于点H，AB = 3. 若EC = 1，求DG的长.

解决方法是连接EG（如图13），通过线段垂直平分线的性质及勾股定理可得DG =[53].

但细细斟酌后发现该问题与后面要研究的内容几乎毫无关联，而“十字形”作为整个问题的主心骨是第（2）小题第①问及第（2）小题第②问研究路径的重要前提，若不在首问中体现出来线段间的关系，会对学生思维的延续造成障碍，故将第（1）小题改为证明FG = DE，既为学生的思维搭建了阶梯，又承担了全盘托底的重要功能. 此外，由于第（1）小题直接取材于教材，所以正确率应该较高. 从题目整体设计来看，第（1）小题起点较低，问题情境学生易于理解，学生能根据问题较好地调用已有经验，为后面深入分析问题提供思维基础，符合学生的认知发展规律.

（2）搭建“脚手架”需要边界.

① 给出支点让思路水到渠成.

题目快成型之时，对于有一处是否需要改动，笔者思索许久，即是否需要帮助学生将IE连好. 连的好处在于有了IE这条线段后“K型”相似跃然纸上，在“K型”相似的背景下构造二次函数模型，并得出点I呈迂回型轨迹，这对于学生是比较熟悉的，再加上点I与点O的关系，学生便能轻松转化. 但这样是否会失去一些探究的乐趣呢？带着这样的疑问，笔者将整个命题思路重新梳理了一遍，发现该题目设置的初衷是希望学生能够运用转化思想，但如果没有IE这条线段，学生可能就察觉不到关于点I的二次函数模型. 而当失去了对点I的“想象”后，学生很难再将点O与点I产生思维联系. 转化思想与函数建模同时出现已经增加了难度，若再要学生寻找这条辅助线就会让题目变得处处磕碰. 适当设置一个合理的支点并不会让题目显得索然无味，反而更能激起学生进行有逻辑地探究，拾级而上才能站得更高.

② 收回指引让策略四通八达.

在历经百般思考与打磨之后，最终决定将这道题编制出来. 但在进行难度综合考量时，发现该题难度略微大了一些，考虑要不要再给学生增加一个“脚手架”，让该题非常浓厚的“代数味”更容易被接受，让学生更轻松地想到用代数思维去解决几何问题，以理性驾驭感性. 若帮学生设好未知数，令CE = x，相信学生在解决第（2）小题时就会计算出BE = 3 - x，BI =[-13x2+x]，CG =[-16x2+32]，BE + BI =[-13x2+3]，BE + BI刚好是CG的2倍. 同时，在有了BI的表达式后，学生更容易发现BI的长度是一个二次函数，点I的运动路径就直接呈现出来了. 这样修改无疑可以给予学生更加明确的方向，也降低了题目的难度，但似乎该题的“探究味”也淡了许多，失去了很多本来应有的色彩，更像是一道“计算题”了. 或许有的学生会像笔者设计第（2）小题时一样，站在整体的角度综合分析各条边之间的数量关系求解，或许有的学生能够设两个未知数，如CE = a，CG = b，用更简单的代数运算去证明. 但是有了一个明确的指令后，这些“天外来物”都会“烟消云散”，哪怕略有一些难度，也要留给学生更多想象的空间，营造“条条大路通罗马”的解题氛围.

四、两点思考

1. 以少寓多方可包罗万象

命制一道几何综合题自然需要多包含一些要素让题目更有层次感与趣味性，但这种“复杂”不能建立在“烦琐”的基础上，而是要以“极简”的形承载“有层次”的核. 这需要命题人对初中阶段的几何图形及知识之间相互的关联有较深刻的理解，以少的结构寓多的内涵. 该题有这样几处遵循了“以少寓多”的命题理念. 首先，是素材的选择. 该题选择教材上较为简单的“十字形”模型为素材，在不添加任何线段的情况下，只是让图形“动”了起来，并将“十字形”中的一条线段设定为另一条线段的垂直平分线，再取该线段的中点，题目的雏形就此完成. 就是在这样平平无奇的图形中，却能探索图形运动过程中线段之间的数量关系与变化中的不变规律. 第（2）小题第②问涉及的转化思想、函数建模思想、轨迹思想都具有一定的综合性与发展性. 虽然以简单的图形起步，但稍作改编后却是精彩纷呈的大千世界. 其次，在第（2）小题两问的设置上最终没有继续添加条件“设CE = x”作为“脚手架”，适当留白才会给学生无限的可能. 命题者毕竟只有一个人的想法，而学生却有一群人的智慧，以自己的假设去揣度学生的思想是主观的，是具有掠夺性的，反而会限制学生的思路，使学生的思路变得狭隘，以少的牵引迸发多的灵感或许更能从解决问题的层面发展学生的数学核心素养. 最后，笔者近期又对该图形展开了研究，发现在给定线段垂直平分线的基础上，尝试只添加一条辅助线构成新的图形有三种方式，分别是连接BD交FG于点O（如图14），连接AC交FG于点O，交DE于点I（如图15），连接EF（如图16）. 这些图形都有很多值得研究的地方，在此不一一赘述. 看来一个真正意义上的好图形是不需要过于复杂的包装的. 越是简单，反而越能给予教师和学生更多的思考空间与可能性.

2. 循序渐进便能浑然天成

命制试题是一项急不得的慢活，就如泡一杯茶，盖一座房子，需要按照步骤一步一步进行，最终才能呈现出一道好题. 该题从图形探索到首问的设置再到支点的推敲无不循序渐进，从大局出发，整体与部分相结合地调整与打磨. 在图形探索阶段，从静态图形开始，通过增加一个变量让其“动”起来，经历了从“确定”到“任意”地扩大研究范围，再从“任意”到“确定”地寻求研究内容，以结构严密的命题方式最终确定了研究对象. 在问题设置阶段，注重首问的铺垫性，紧紧围绕该题的基本结构“十字形”展开，设置证明“十字形”的首问可以在方法与策略上引导学生完成对后续问题的深入思考与探究，使得题目更具有连贯性与探究性，更符合初中生现有的认知水平，主线、支线双线并进使得题目条理分明、主次突出. 在添加“脚手架”阶段，发现在研究动点O与可转化的动点I之间存在着太多的思维难点. 对学生来说，要想在轨迹探究、主次分析、转化思想、构造中位线等方面一步到位是非常困难的. 而给出辅助线IE后便能拉近点I与点O的距离，让学生能够更自然地找到转化的方向，使解题一气呵成，浑然天成.

参考文献：

［1］钱德春. 变化中的不变 任意中的确定：对一类函数试题特点及教学指向分析［J］. 中学数学杂志，2019（8）：32-36.

［2］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.