素养导向的初中几何起始单元教学策略

摘 要：在几何的起始单元教学中，要引导学生经历从现实情境中抽象出几何图形的活动，分析小学阶段几何研究方法的局限性，提出几何的研究内容，用推理论证的方法研究几何图形的性质和关系的必要性. 引导学生经历分离构成所有几何图形的基本要素活动，了解点、线、面、体的概念及它们之间的联系，用点、直线、平面这三类几何基本元素有逻辑地构造图形是论证几何的基础.

关键词：素养导向；初中几何；起始单元；教学策略

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）09-0025-05

引用格式：王华，吴增生. 素养导向的初中几何起始单元教学策略［J］. 中国数学教育（初中版），2024（9）：25-28，50.

初中阶段注重用推理论证的方法研究几何图形，体会欧几里得几何的基本思想和基本框架，进一步发展学生的空间观念、几何直观和推理能力，这需要追本溯源与逻辑建构. 这种追本溯源的过程为：先从实物中抽象出几何图形，分离出构成几何图形的基本元素，得到三类基本几何对象——点、直线、平面，然后通过尺规作图和运动变化有逻辑地构造直线、射线、线段、角、相交线、平行线、多边形、圆等几何图形，初步建立有逻辑的几何直观. 而逻辑建构的过程为：基于直观抽象图形与图形关系，通过定义明确论证对象，通过抽象基本事实确立论证的起点，通过证明确立论证的逻辑，通过命题确立论证的结果，构建初中几何命题的逻辑体系. 因此，在初中几何起始单元的教学中，教师应该注重设计直观观察与想象的活动，以及在此基础上的抽象活动，引导学生抽象几何图形的概念，认识立体图形和平面图形，建立点、线、面、体等概念体系，为用推理论证的方法研究几何图形及其关系奠定基础.

一、几何起始单元的主要内容和育人价值

初中几何起始单元“几何图形”的学习内容主要包括几何图形、立体图形、平面图形，平面图形与立体图形的关系，点、线、面、体及其关系. 该部分既是从直观的实验几何到论证几何的过渡内容，也是后面形成直线、射线、线段和角等几何概念，建立相关基本事实的基础. 小学阶段，从具体图形出发，学生经历了用直观的方法认识线段、射线、直线、角、三角形、四边形、圆等平面图形及长方体、正方体、圆柱体、圆锥、球等立体图形，并通过从不同的方向看和展开折叠活动认识立体图形的特征、立体图形与平面图形的关系. 初中阶段，则需要从实物中抽象出几何图形，进一步认识平面图形与立体图形之间的区别与联系，分离能构成所有几何图形的基本元素——点、线（主要是直线）、面（主要是平面），即希尔伯特所说的“直线几何基本元素——点，平面几何基本元素——点、直线，空间几何基本元素——点、直线、平面”，并着重在平面上建立基本事实，用推理的方法研究点与点、点与直线、直线与直线及由线段经过组合、交叠、运动所形成的三角形、四边形、圆等几何图形的性质和关系. 欧几里得的《几何原本》中，基于直观给出点、直线、平面的描述性“定义”，建立五条公设、五条公理来规定几何元素的关系，建立论证几何的基础，初中几何中点、线、面、体及其关系也是基于直观进行抽象的.

以点、线、面、体及其关系为核心内容的初中几何起始单元教学，起着从小学阶段的实验几何过渡到初中阶段的论证几何的作用，承担着做好中小学内容的衔接，激发学生学习兴趣的任务，能够让学生体会小学阶段直观研究方法的局限性，了解推理论证的几何研究方法，体会推理的必要性，从而发展学生的推理能力. 通过让学生经历抽象点、线、面等几何基本元素及其关系的活动，能进一步发展学生的空间观念，帮助学生建立几何直观，发展学生的抽象能力.

二、素养导向的几何起始单元教学策略

策略1：开展观察想象及回顾反思活动，提出初中几何的研究内容和研究方法.

（1）通过直观观察与想象建立初步的几何直观.

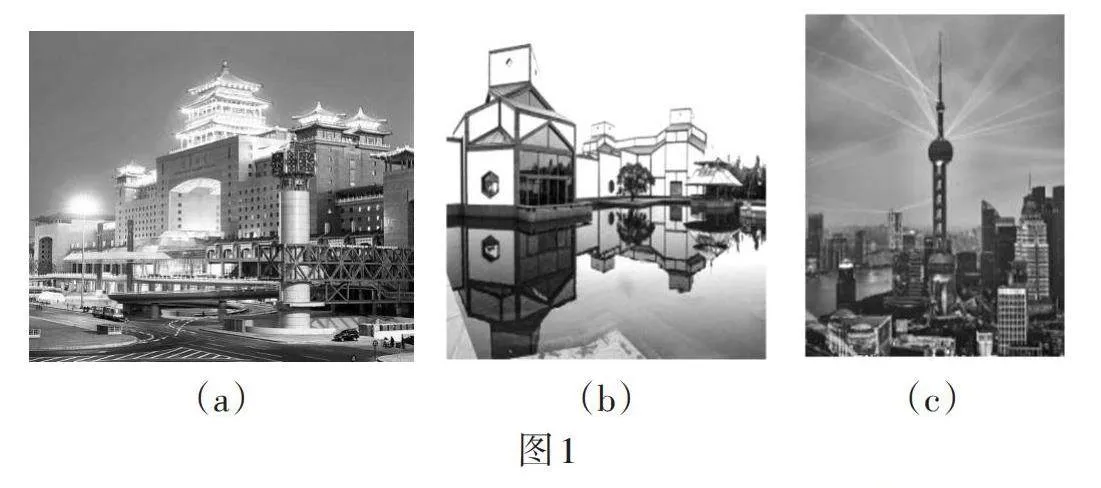
引导学生观察和想象如图1所示的图案中的现实情境，从中识别小学阶段学习过的几何图形，从而激发学生学习几何的兴趣，初步建立各类图形的几何直观.

（2）通过回顾思考总结小学所学的几何知识及学习的方法.

让学生回顾小学阶段学习了哪些几何图形，获得了哪些知识，是怎样获得这些知识的. 例如，小学阶段学习过立体图形和平面图形，知道了长方体、正方体、圆柱、圆锥、球等立体图形，能从不同的方向看立体图形，会展开长方体、正方体和圆柱，认识了线段、射线、直线和角，知道了直线的平行和垂直关系，认识了三角形、四边形、平行四边形、圆等平面图形，会测量线段的长度、角的度数，学习了三角形的内角和等于180°，学会了计算三角形、平行四边形、长方形、正方形、圆的周长和面积等. 进而引导学生总结小学的学习方法——观察、想象、测量、实验、归纳等.

（3）通过反思和质疑体会推理论证的必要性.

通过引导学生质疑小学阶段得到几何图形性质的可靠性与普适性，让学生知道用演绎推理的方法获得确定和普适结论的必要性. 例如，以“三角形的内角和等于180°”的学习为例，引导学生提出质疑，通过有限个三角形的测量和拼角实验得到这一结论不能说明对所有的三角形都成立，让学生体会用新的方法说明这一结论对所有三角形（无数个三角形）都成立的必要性，指出在初中阶段我们将学习这种新的研究图形及其关系的方法——推理论证的方法.

（4）提出初中几何的研究内容和研究方法.

引导学生思考如何用推理的方法研究所有的几何图形，不是逐个研究图形，而是要进行一般性研究. 首先，需要明确研究对象——什么是几何图形；其次，明确几何研究的基本内容——研究物体的形状、大小和位置关系；最后，提出初中几何研究的主题——用推理论证的方法研究物体及几何图形的形状、大小和位置关系.

教学策略1主要体现在章引言的教学活动中.

策略2：开展抽象几何图形及其关系的活动，发展空间观念、几何直观和抽象能力.

（1）通过实物的观察与想象抽象立体图形及平面图形的概念.

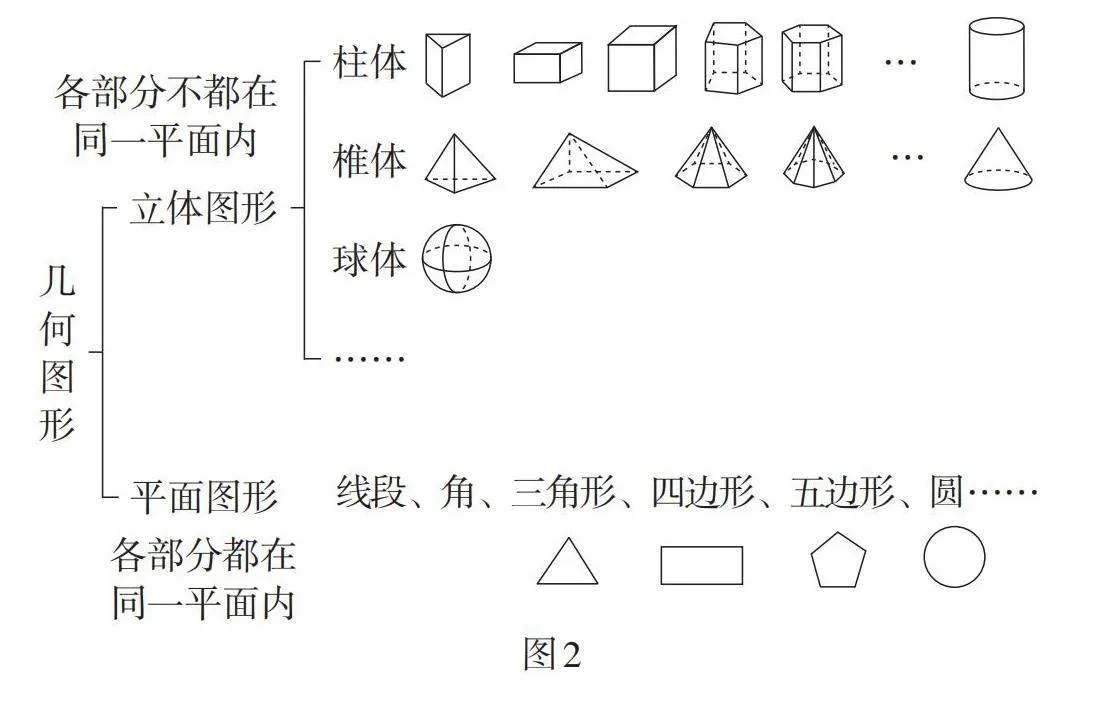
如图2，通过观察类似图1的情境中不同物体的结构，引导学生从形状、大小、位置的角度观察实物，获得立体图形和平面图形的概念，认识立体图形与平面图形的异同.

（2）建立立体图形与平面图形之间的联系.

通过设计从不同的方向看几何体的活动及展开与折叠几何体等活动，建立立体图形与平面图形之间的联系，发展空间观念，建立几何直观.

策略3：开展抽象几何基本元素及其关系的活动，发展空间观念、几何直观和抽象能力.

（1）引导学生经历分离构成几何图形的基本元素活动.

寻找能构成所有研究对象的基本元素，分析基本元素构成研究对象的普适机制，重构对象并研究其属性和关系，这是追本溯源地研究问题的基本思路. 用演绎推理的方法研究几何也是如此进行的. 先分离能构成所有几何图形的基本元素，即点、直线、平面；再分析由这些基本元素构成几何图形的普适方法，即尺规作图和运动变化，抽象出用这些基本元素构建几何图形的逻辑机制，形成基本事实；最后，根据基本事实，利用尺规构建图形，用演绎推理的方法研究图形的属性和关系.

在具体教学过程中，教师可以先对上述追本溯源的过程作简要介绍. 在此基础上，通过让学生观察各种立体图形和平面图形，使其体会点是构成图形及5f73136df1b0f77ab6e0f9b49c8fc0421da29600ab5bb2285c7b13623b32101d空间的最基本的元素，点、线、面能组成所有的几何图形. 点是直线的基本元素，点和直线是平面的基本元素，点、直线、平面是空间的基本元素. 这里，要设计观察三维空间中的几何体——长方体，分离出其各个侧面的活动. 通过想象形成平面的视觉表象，分离出棱并通过想象建立直线的视觉表象，通过观察长方体的顶点并想象切割棱建立点的视觉表象. 进一步地，通过只关注空间中物体的位置，把位置抽象成几何中的点，通过用沙粒堆沙堆的实例，把几何图形（包括直线、平面、三角形、长方体等）及空间看成由无数个点组成的点集，让学生体会点是构成所有图形的最基本的元素. 研究空间中点的位置关系是几何学研究的最基本问题.

（2）引导学生通过观察和想象建立点、线、面、体之间的联系.

首先，设计适当的观察和想象活动，帮助学生建立点、线、面、体之间联系的静态直观. 例如，通过观察长方体，让学生知道长方体由6个长方形的面围成，而长方形则由4条线段围成，长方体有8个顶点，围成长方形的线段由点排成. 这样就用静态的观点抽象得到构成几何图形的基本元素之间的联系.

其次，可以对3D打印过程的观察和想象，形成点动成线、线动成面、面动成体的动态直观，也可以让学生经历用笔画线，快速转笔和旋转直立硬币等活动，通过观察和想象形成点动成线、线动成面、面动成体的动态直观，让学生知道点沿着同一方向移动形成“直”的线，点沿着不同的方向运动形成曲线. 通过让学生想象直线按照固定的方向运动构成平面，平面沿着固定的方向运动构成三维空间的过程，使学生初步认识欧氏空间的连续性和平直性，知道欧氏空间（一维空间、二维空间、三维空间）是线性空间，体会点、直线和平面是欧氏空间的基本元素，这些基本元素之间的关系（结合、顺序、合同、连续、平行等关系）是欧氏几何的基本研究内容.

三、系统贯彻这些教学策略的途径——单元整体设计与课时落实

在教学实践中，可以通过单元整体设计、课时落实的思路系统贯彻上述教学策略.

1. 设计单元教学主线

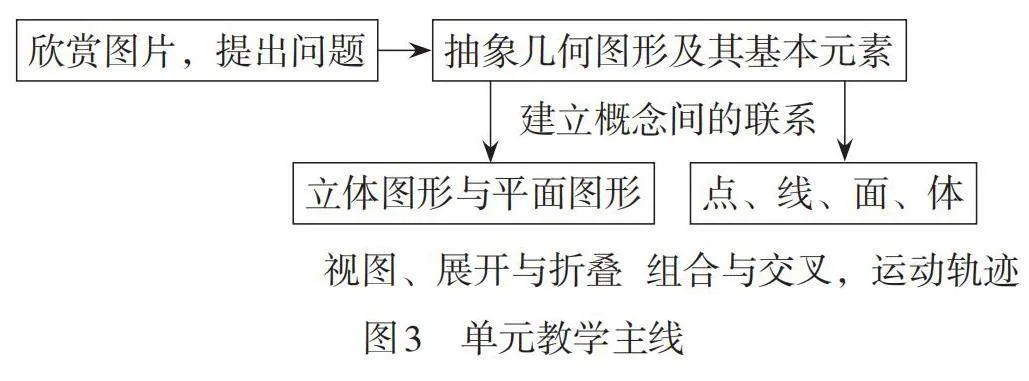
首先，根据单元知识发生发展的逻辑，设计单元教学主线.“几何图形”这一论证几何起始单元的知识发生发展的逻辑是：欣赏丰富多彩的图形，提出几何研究的内容及新方法，从实物中抽象出几何图形，建立立体图形和平面图形的概念，建立立体图形与平面图形的联系，分离出几何基本元素（点、直线、平面），建立点、线、面、体之间的联系，为进一步抽象直线、射线、线段、角等基本概念，建立相关的基本事实奠定基础. 根据这一知识发生发展的逻辑脉络，可以设计“立体图形和平面图形”单元的教学主线，如图3所示.

[欣赏图片，提出问题][抽象几何图形及其基本元素][立体图形与平面图形][点、线、面、体][建立概念间的联系][视图、展开与折叠][组合与交叉，运动轨迹] [图3 单元教学主线]

2. 设计核心素养导向的单元教学目标和课时教学目标

用“经历……，能、会、知道或体会……，发展……”的范式，设计融合“四基”“四能”和发展空间观念、几何直观、抽象能力等素养的单元教学目标，并针对单元教学目标，根据课时教学内容设计课时教学目标.

根据《义务教育数学课程标准（2022年版）》的内容要求及相关核心素养行为表现的内涵，设计如下的“几何图形”单元的教学目标.

（1）经历欣赏丰富多彩的几何图形的活动，激发学习几何的兴趣；经历回顾小学阶段学习过的几何图形及其研究方法的活动，通过质疑用直观的方法获得的结论的可靠性和普适性，体会用推理论证的方法研究几何图形及其关系的必要性，提出推理论证的新方法.

（2）经历从实物中抽象出立体图形和平面图形的概念，提出几何研究内容的活动，知道几何学是研究物体的形状、大小和位置关系的科学，能识别长方体、正方体、棱柱、圆柱、圆锥、球等简单的几何体，能辨别立体图形与平面图形，进一步发展空间观念、几何直观和抽象能力.

（3）经历从不同的方向看几何体，以及几何体的展开和折叠活动，能建立立体图形与平面图形之间的联系，发展空间观念，建立几何直观.

（4）经历分离几何基本元素点、直线、平面的活动，知道其意义，能用静态和动态的观点分析点、线、面、体之间的联系，建立几何直观，发展抽象能力.

在此基础上，设计不同课时的教学目标，明确其教学重点，通过学情分析确定教学难点. 例如，在第1课时“立体图形和平面图形”，设计的教学目标、重点和难点如表1所示.

3. 根据课时教学目标设计教学活动

有了课时教学目标和重点、难点，就可以根据课时教学目标设计教学活动，根据活动需要设计驱动性问题和任务，引导学生参与数学活动，设计启发性问题启发学生思考，并通过交流评价确定活动中发展核心素养的效果.

例如，针对教学目标（1）开展章引言教学，可以设计欣赏图片，回顾小学阶段学习的几何知识，评价质疑的活动，再根据活动的特点、育人价值设计驱动性问题和任务，进行启发性提问. 教学过程如下.

引言：丰富多彩的图形美化了人们的生活，无论是宏伟的大型建筑，还是精致的生活用具，都含有各种各样的几何图形. 在初中阶段，我们将在小学的基础上进一步研究几何图形及其关系.

问题1：在小学，我们已经初步认识了几何图形，你能说说学了哪些知识吗？是怎样学习的？

师生活动：学生回顾认识了线段、射线、直线、三角形、平行四边形、圆、正方体、长方体、圆柱等图形，会画线段并能测量线段的长度，知道了“三角形的内角和为180°”，会求三角形、平行四边形及圆的面积，等等.

问题2：小学中，我们通过测量和归纳得到“三角形的内角和为180°”，你觉得可信吗？

师生活动：教师引发学生质疑，提出需要进一步学习能使人信服的说理方法研究几何图形及其关系，即推理的方法. 学生思考、小组讨论.

【设计意图】通过创设情境，激发学生的学习兴趣，做好中小学内容的衔接，通过质疑使学生体会推理论证的必要性.

再如，针对教学目标（2）和教学目标（3），为了抽象几何图形的概念，建立点、直线、平面、几何体的视觉表象，可以设计如下的教学片断.

问题：如图4，如果只关注纸盒的形状大小，那么它是小学学习过的哪一类图形？你还能举出具有这种外形的其他物体吗？

追问1：观察长方体的各个面，看到的图形是什么？

追问2：长方体的各个面是由什么图形围成的？各条棱是什么图形？长方体的棱的端点是什么几何图形？

追问3：把线段向两端无限延伸，给我们什么图形的形象？把长方形或正方形向上、下、左、右四个方向无限延伸，给我们以什么图形的形象？把长方体向上、下、左、右、前、后六个方向无限延伸，给我们以什么图形的形象？

师生活动：学生观察包装盒的外形，从中抽象出长方体，并列举长方体形状的物体，观察长方体的各个面，抽象出长方形、正方形，观察长方体的棱及其端点，抽象出线段和点.

教师在此基础上给出几何图形的概念，并指出几何图形是数学研究的主要对象之一. 进一步引导学生想象，把线段向两端无限延伸，给我们以直线的形象，把长方形和正方形向上下、左右四个方向无限延伸，给我们以平面的形象，把长方体向上、下、左、右、前、后六个方向无限延伸，给我们以（三维）空间的形象.

【设计意图】让学生从实物中抽象出几何图形，形成直线、平面和空间的直观表象，建立几何直观，发展抽象能力.

四、结束语

基于数学的整体性分析单元内容的地位、作用和逻辑关系，分析知识的发生发展过程和应用知识过程中蕴含的发展核心素养的育人价值，在此基础上研究发展数学核心素养的教学策略，并通过单元分析和课时教学具体贯彻落实，这是在数学教学中把发展数学核心素养的育人目标落到实处的根本策略. 该单元的教学实践表明，在这样的教学活动中，能让学生在具体的数学活动中学会直观观察与想象，学会追本溯源地思考，学会从现实情境中抽象出图形与图形关系，学会分离几何基本元素，建立点、直线、平面和几何体的联系，直观理解欧氏空间的平直性和连续性，有效促进学生空间观念、几何直观和抽象能力的发展.

参考文献：

［1］ 中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］ 希尔伯特. 希尔伯特几何基础［M］. 江泽涵，朱鼎勋，译. 北京：北京大学出版社，2009.

［3］ 欧几里得. 欧几里得几何原本：第3版［M］. 兰纪正，朱恩宽，译. 西安：陕西科学技术出版社，2020.