“双减”背景下初中数学单元作业设计实践与思考

摘 要：以“解直角三角形”单元为载体，关注“教—学—评”一致性，从理解课程标准定方向、设计载体定作业、创新评价定成效三个方面形成作业设计策略. 通过作业设计淬砺教师专业素养，激发学生的学习热情，发挥作业的育人功能.

关键词：单元整体视角；作业设计；解直角三角形

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）09-0015-05

引用格式：张淑婷.“双减”背景下初中数学单元作业设计实践与思考：以“解直角三角形”单元为例［J］. 中国数学教育（初中版），2024（9）：15-19.

一、单元作业设计的必要性

作业是学生学习过程中的一种自主性、探究性、有意义的学习活动，可以检验学生对学习内容的掌握程度，对于提升学习效能具有积极作用.《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》（以下简称《意见》）中指出，要有效减轻学生作业负担，提高作业设计质量，加强作业完成指导. 作为数学教师，我们要积极探索初中数学单元作业设计策略，减轻学生的课业负担，确保学生深度学习，进一步提升教学效果，发展学生的数学核心素养，让作业真正成为教师教和学生学的“桥梁”.

下面以浙教版《义务教育教科书·数学》九年级下册（以下统称“浙教版教材”）“解直角三角形”单元为例，重点关注知识的前后联系和解决实际问题的方法（将实际问题抽象为数学问题），通过作业设计和实践，提出对单元课后作业设计的思考.

二、整体优化单元作业设计

教师要从整体视角理解课程标准与教材，确定单元教学目标，明确课时教学目标和课后作业目标，从落实基础、提炼方法、加强应用等方面设计作业，并创新评价形式，实现“教—学—评”的一致性. 一般地，单元作业设计的策略如图1所示.

1. 理解课程标准：定方向

（1）单元作业设计的目标.

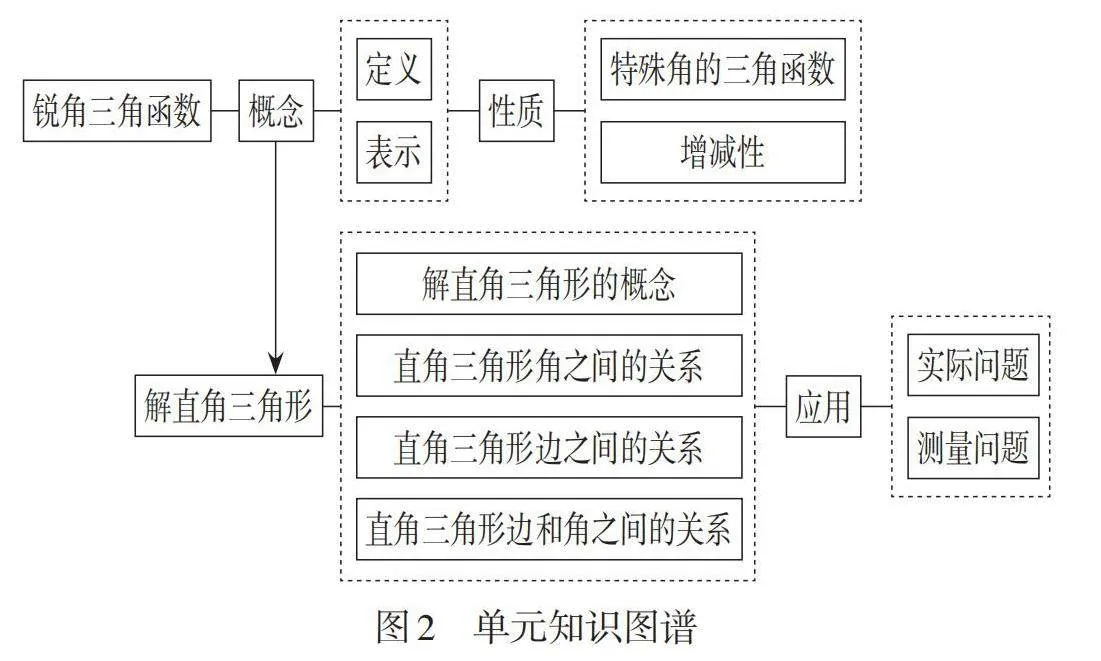
《义务教育数学课程标准（2022年版）》（以下简称《标准》）中对锐角三角函数的要求如下：（1）利用相似的直角三角形，探索并认识锐角三角函数（sin A，cos A，tan A），知道30°，45°，60°角的三角函数值；（2）会使用计算器由已知锐角求它的三角函数值，由已知三角函数值求它的对应锐角；（3）能用锐角三角函数解直角三角形，能用相关知识解决一些简单的实际问题. 在《标准》的基础上，笔者充分研读浙教版教材，确定了如图2所示的单元知识图谱.

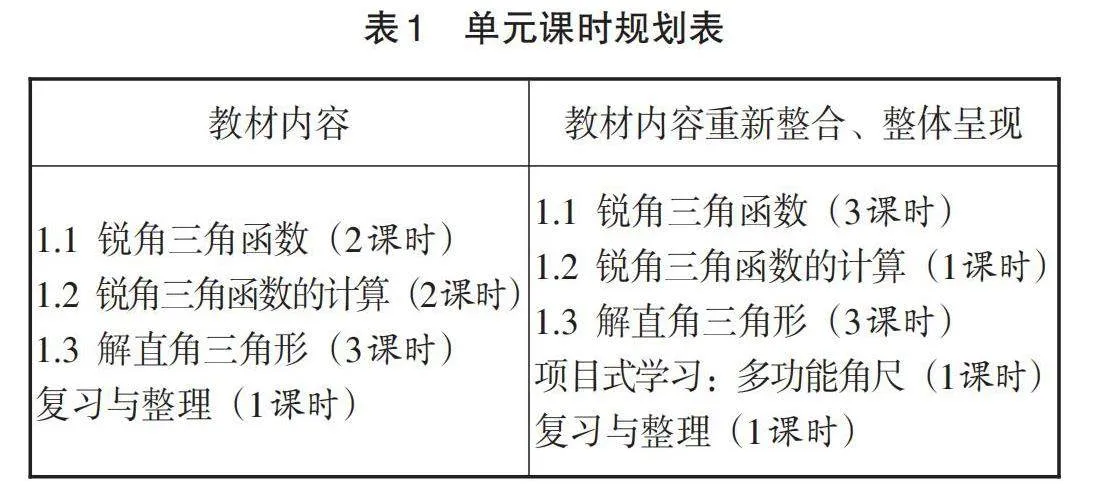
根据单元知识图谱，在单元整体视角下确定单元课时方案，如表1所示.

结合学情，将“1.1 锐角三角函数”增加1个课时，为后续研究锐角的余弦、正切的概念提供范例；增加项目式学习的内容，旨在培养学生应用所学知识创造性地解决问题的能力，发展学生的应用意识和创新意识.

根据对《标准》和浙教版教材的分析，确定每课时的教学目标，要对教学目标和作业目标进行区分，作业目标一定是可测的. 以“1.3 解直角三角形”第3课时为例，其教学目标和作业目标如表2所示.

（2）单元作业设计的原则.

“双减”背景下，教师要平衡好减负和提质的关系，重视作业设计的针对性、层次性和多样性. 有针对性（有效性）的作业应该基于教学目标和教学过程中学生的表现来设计，要指向作业目标的达成情况，反映课堂教学中的知识和数学思想方法. 作业设计还要注重层次性，可以根据学生的层次设计作业，针对同一问题从多角度设问，使各个层次的学生都能有所收获. 在常规作业的基础上，可以设计多样性（个性化）作业，帮助学生走向生活、走向实践，在真实而充盈的体验中完成对知识的内化.

（3）单元作业设计的形式.

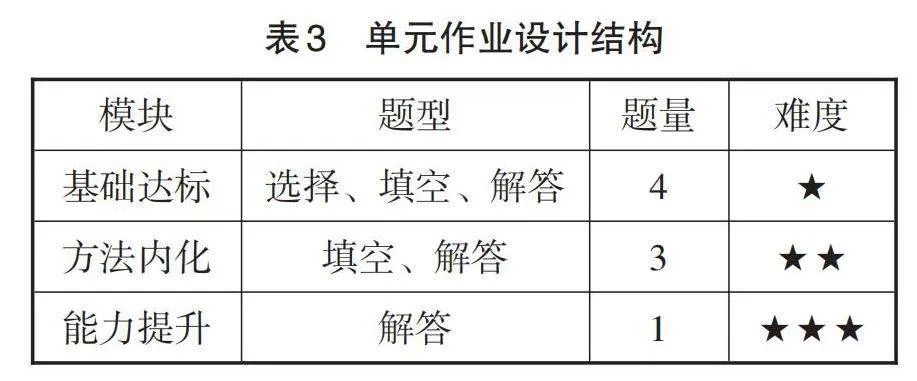
调查发现，与生活贴近、综合运用知识解决问题、方法巧妙的作业题更容易使学生印象深刻. 因此与作业容量相比，提高作业质量更能提升学生的学习水平.《教育部关于加强初中学业水平考试命题工作意见》中指出，要提升试题科学化水平，减少机械记忆试题和客观性试题比例，提高探究性、开放性、综合性试题比例，积极探索跨学科命题. 单元作业的设计要强调同一单元不同课时作业结构的统一和层次上的递进. 从知识、能力等方面出发，统一单元作业结构（题型、题量、时长等），如表3所示.

设计作业时应设计题卡，即写出每道作业题的知识点分类、检测目标解析、答案与解析和预估难度，以便根据学生的作业完成情况及时调整教学策略.

案例1：“1.1 锐角三角函数”第1课时作业题卡设计.

作业题：如图3，在△ABC中，sin B =[13]，tan C =[22]，AB = 3，则AC的值为___________.

此题的作业题卡设计如表4所示.

【设计意图】作业设计一定要基于“教—学—评”的一致性. 将其以题卡的形式呈现，能够方便学生和教师检验教学目标和作业目标是否达成一致.

2. 设计载体：定作业

（1）落实基础，层层递进.

作业能反映学生基础知识和基本技能的达成情况. 教师要设计符合学生年龄特点和学习规律、体现素质教育导向的基础性作业；将大量习题进行分类归整，设计有层次的练习题，引导学生在分层习题训练中对数学知识进行深度思考，举一反三.

案例2：“1.1 锐角三角函数”第1课时分层作业设计.

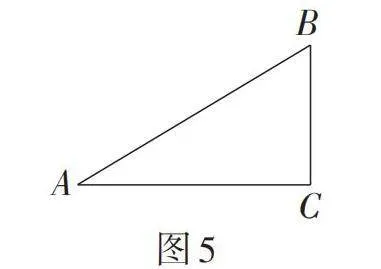
第1题（★）：（1）如图5，在Rt△ABC中，∠C = 90°，AC = 5，BC = 3，求sin A的值.

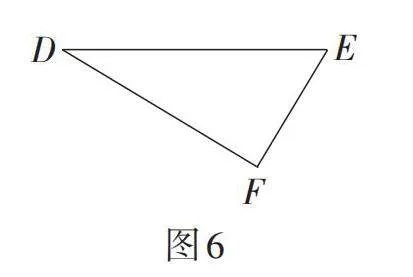
（2）如图6，在Rt△DEF中，∠F = 90°，DE = 4，EF = 2，求sin E的值.

第2题（★）：在Rt△ABC中，∠C = 90°，AC∶BC = 5∶3，求sin A的值.

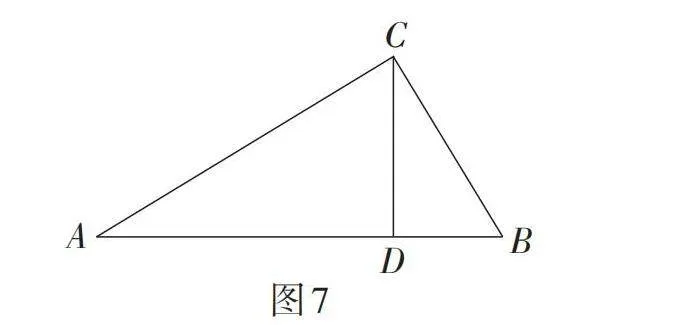
第3题（★★）：如图7，在Rt△ABC中，∠ACB = 90°，CD ⊥ AB，垂足为点D. 若BD =[95]，CD = 3，求sin A的值.

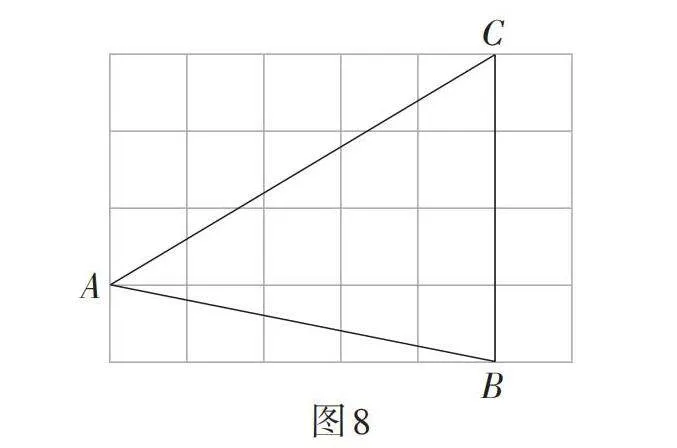
第4题（★★★）：如图8，在4 × 6的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在这些小正方形的顶点上，求sin∠ACB的值.

【设计意图】第1题旨在考查学生根据已知直角三角形的边长求一个锐角的正弦值，巩固正弦的概念，并通过改变三角形的位置进行强化. 第2题旨在考查学生根据已知条件画图，通过边之间的比例关系求锐角的正弦值，渗透了数形结合思想. 第3题旨在考查学生能否发现同一个锐角在不同的直角三角形中所对的对边和斜边比值相同. 第4题旨在考查学生能否在格点中构造锐角所在的直角三角形，并进行计算. 给出网格的背景，即给学生构造直角三角形创造了隐含条件，为后续添加辅助线的方法作铺垫. 这样的作业设计层层递进，能帮助学生深入理解正弦的概念，而基于变式的化归是数学问题解决的基本思路.

案例3：“1.1 锐角三角函数”第3课时分层作业设计.

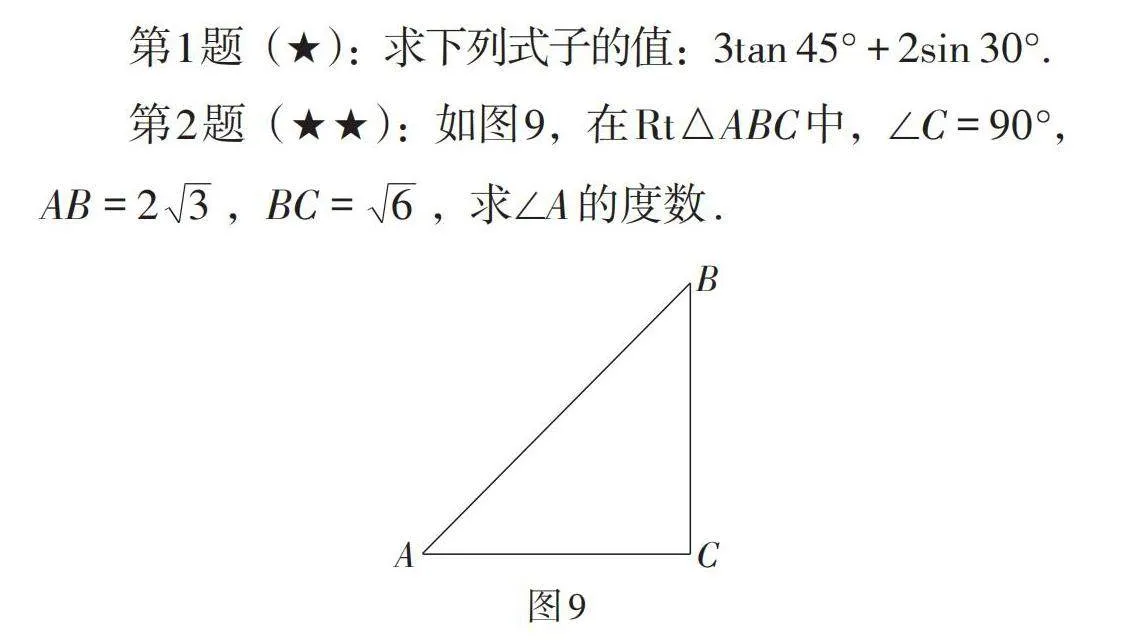
第1题（★）：求下列式子的值：3tan 45° + 2sin 30°.

第2题（★★）：如图9，在Rt△ABC中，∠C = 90°，AB =[23]，BC =[6]，求∠A的度数.

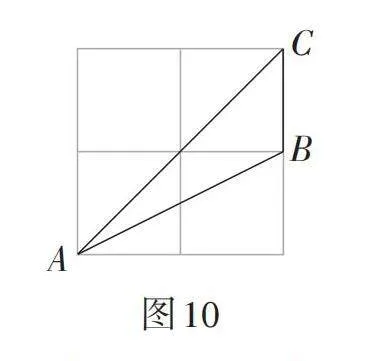
第3题（★★★）：如图10，点A，B，C均在2 × 2的正方形网格的格点上，每个小正方形的边长都是1，求sin∠BAC的值.

【设计意图】第1题旨在考查学生对特殊锐角的三角函数值的计算. 第2题在第1题的基础上设计，旨在考查学生能否根据已知锐角三角函数值求对应的特殊锐角，为锐角三角函数的计算的学习作铺垫. 第3题旨在考查学生对含有特殊锐角的三角形中的角的三角函数值的计算. 网格中三角函数值的计算与案例2中的第4题相呼应，也需要构造直角三角形，但难度有所提升，增强了同一单元不同课时作业之间的递进性，考查学生对知识的综合运用能力，发展学生的几何直观素养.

（2）凸显方法，把握关联.

学数学更重要的是掌握方法. 教师要聚焦单元教学目标设计综合性作业，将前后知识点串联到作业题中，以作业为依托帮助学生构建知识体系，强化学生对所学知识的认知与理解，培养学生的知识迁移和综合运用能力.

案例4：“1.3 解直角三角形”第3课时综合运用知识解决问题.

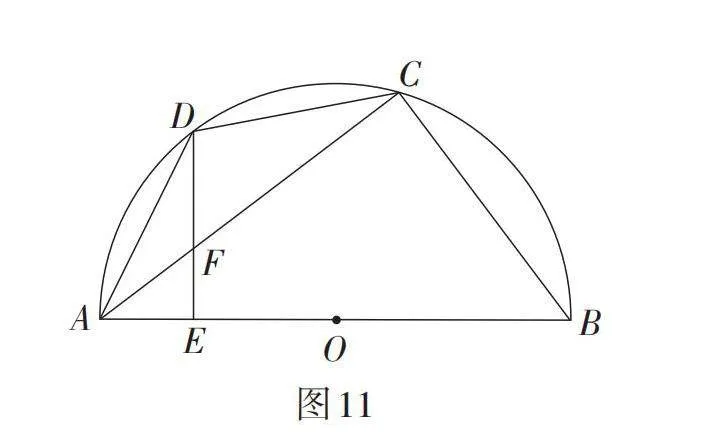
作业题：如图11，四边形ABCD内接于⊙O，AB为⊙O的直径，AD = CD. 过点D作DE ⊥ AB于点E，连接AC交DE于点F. 若sin∠CAB =[35]，DF = 5，求BC的长.

【设计意图】“1.1 锐角三角函数”和“1.2 锐角三角函数的计算”的内容重在让学生掌握核心概念，从“1.3 解直角三角形”开始可以设计与圆等知识综合的作业题，让学生综合运用已学知识解决与直角三角形有关的问题，进一步培养学生的推理能力、运算能力和模型观念.

（3）回归本质，应用生活.

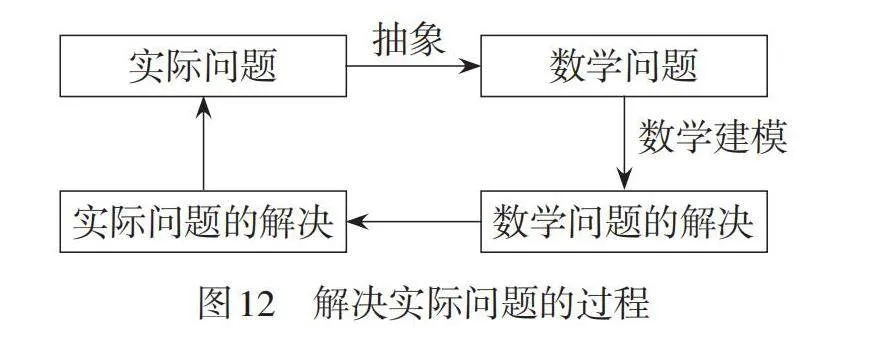
丰富、有趣的实际问题能够激发学生的学习兴趣，帮助学生体验解决实际问题的过程（如图12），培养学生的应用意识，提升学生的抽象能力. 本单元通过设计具有实际背景的作业题，让学生体会解直角三角形在解决实际问题中所起的作用.

[实际问题的解决][实际问题] [数学问题的解决][数学问题] [数学建模][抽象] [图12 解决实际问题的过程]

3. 创新评价：定成效

（1）精反馈.

《意见》指出，教师要认真批改作业，及时做好反馈，加强面批讲解，认真分析学情，做好答疑辅导. 为了提高评价的功能，教师的批改、反馈、讲解需要做到精准. 同时，根据学生的作业完成情况或在作业中发现的问题，教师要及时调整教学策略，有目标地解决问题，真正做到“教—学—评”的一致性.

（2）倡反思.

通过纠错反思、改编探究、整理内化，鼓励学生从作业题中的“点”出发，对作业题进行改编，改变作业题中的条件，增加或减少条件，提出新的问题，再将所有问题连成“线”研究，从变化的习题中发现不变的数学本质，发展学生的数学思维.

案例5：“1.1 锐角三角函数”第3课时作业题的拓展和深入.

第1题：求出15°，75°角的三角函数值.

第2题：以思维导图的形式，整理构建“解直角三角形”单元的知识结构图.

【设计意图】第1题旨在让学生在掌握特殊锐角的三角函数值的基础上，进一步探究15°，75°角的三角函数值，让学生在探究中完成知识的内化. 第2题引导学生用思维导图的形式，从知识、内容等方面自主整理单元知识框架，挖掘思想方法，使本单元的结构更加立体.

（3）创形式.

根据作业设计多样性的原则，可以设计如下新颖型作业：阅读作业（数学史、数学文化）、跨学科作业（注重各学科知识之间的联系）、项目学习作业（利用驱动性问题引发学生创造性地解决问题）等，给学生充分思考、学习、探索、实践的时间，培养学生主动探索的学习习惯.

案例6：“1.3 解直角三角形”第3课时作业设计.

作业题：试列举其他学科中运用三角函数知识研究问题的例子.

【设计意图】三角函数等相关内容与物理知识联系紧密，通过设计跨学科作业帮助学生形成系统化的数学知识.

案例7：“项目式学习：多功能角尺”项目作业设计.

作业题：试设计一把既能测量长度又能测量角度的多功能角尺.

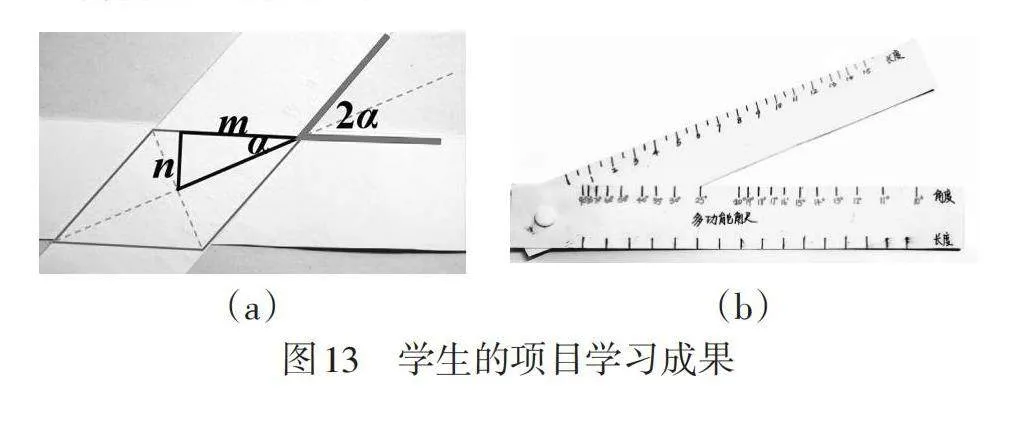
【设计意图】在项目学习的过程中，通过创设结构不良情境，让学生利用三角函数等知识抽象出几何图形，通过分析、计算、测量确定刻度，制作出多功能三角尺（如图13），并进行测量. 根据生活实际，如在装修设计的场景中，可以让学生进一步利用数学知识增加角尺的功能. 例如，测量圆的半径或者不规则区域的周长、面积，等等. 该作业题具有综合性，让学生在解决问题的过程中经历知识的关联与整合，创造出成果，培养了学生的学习能力和知识迁移能力，也是学生高阶认知的过程.

三、几点思考

一份好的单元作业是学生开展自主学习活动的重要载体，是学生实现深度学习、形成素养、培育品格的重要途径，需要教师不断探索.

1. 优化单元作业主题，激发学习热情

作业是学生开展自主学习活动的重要载体，围绕单元主线整体设计少而精的单元作业，让学生有充分思考的时间，建构知识网络并综合运用知识，能够提高学生的类比、迁移的能力，激发学生的学习热情，将“被动学习”转化为“主动学习”.

2. 聚焦单元作业改革，淬砺教师专业素养

教师要以改革为契机，不断淬砺自己的教学基本功，不断学习和研究以提高对教学内容的整体把握，提升作业设计的质量，以专业的思维方式、先进的教育理念、创新的研究视角，不断提升作业设计的水平.

3. 挖掘单元作业功能，发挥育人价值

通过作业设计提升课堂教学质量，让作业真正实现检测、诊断、提升能力的功能和价值. 教师可以丰富作业的形式和内容，也可以设计多学科融合的作业，将数学文化渗透到作业中，让作业承载育人功能，指向核心素养的培育，以及学生综合能力的发展.

参考文献：

［1］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］章建跃. 章建跃数学教育随想录（下卷）［M］. 杭州：浙江教育出版社，2017.