例谈化归思想在初中数学解题中的应用

摘要：化归思想作为一种最基本的数学思想，在初中数学解题过程中

普遍运用，其本质就是将繁琐的问题化为简单易操作的问题，将未知考点转化为已知知识来解答的过程.本文从实数计算、方程或不等式（组）、函数探究、三角函数应用、几何证明等方面结合具体实例进行分析说明，并在研究过程中指导学生应用化归思想，提升其数学核心素养.

关键词：初中数学；化归思想；解题研究

化归思想是一种将问题由困难转化为容易，由繁琐转化为简单的过程，也可以说是转化与归一的总结.化归思想在初中数学教学中经常涉及，在平时的解题过程中也都能体会到化归思想的重要性.

1化归思想的本质特点

化归思想是学生在解决数学问题时常用的一种思想方法，其本质就是在解决问题过程中，把需要解决的问题通过已知知识进行转化，归结形成另一个比较简单的问题，或是可以用已学知识解决的问题，这样就可以通过解决这个简单或利用已知知识能解决的问题达到解决原始

问题的目的.［1］归根到底化归的实质就是转化.

2化归思想在数学解题过程中的具体应用

化归不仅是初中数学中一种重要的解题思想，也是一种问题突破的最基本思维策略，更是一种问题研究过程中有效的数学思维方式.［2］因此在解题过程中使用化归思想进行分析研究，解答问题会取得意想不到的效果.

2.1化归思想在实数计算过程中的应用

以人教版《义务教育教科书数学七年级上册》第一章《有理数》教学为例，教师先引入“相反数”这个概念并把握“有理数的加法运算”，再学习“有理数的减法”，这就将减法问题转化为已经熟悉把握的加法问题，学习了“倒数”知识点后，将有理数的除法运算转化为乘法运算来解答，这样难以表述的问题很自然地就可以解决了.正负数的减法就化归为已经解决的正负数的加法了，而引入“倒数”这个概念后，正负数的除法就化归为已经解决的正负数的乘法了.具体案例如下.

例1数学问题：计算12+122+123+124+…+12n（其中n是正整数，且n≥2）.

问题研究：直接计算上述问题，显然对于七年级的学生来说很难，但是

转化一下思想，将问题运用数形结合的思想方法，通过不断地分割一个面积为1的正方形（如图1），把问题中的数量关系和所分割的几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究，这个问题就容易解决了.

具体操作如下.第1次，分别连接各边中点得到图2，第2次，将图2右下角正方形按上述方法再分割得到图3，……，以此类推.当进行第n次操作后，将右下角最小正方形剪去，剩余图形的面积是1-12n.

2.2化归思想在方程或不等式（组）“消元”问题中的应用在计算一些特殊的方程或不等式（组）问题时，也是利用化归思想将疑难方程进行转化，将“多元”的转化为“一元”的，将“特殊”形式转化为“常规”形式进行解答.［3］例如，我们学习了一元一次不等式（组）的解法后，可以通过化归思想来突破一元二次不等式的解法，以此解决后面的问题.具体案例如下.

例2解一元二次不等式x2-4＞0.显然，这样的问题已经远远超出学生的知识学习范围，但是可以将整式x2-4进行分解因式，得x2-4＝（x+2）（x-2）.

∵x2-4＞0，∴（x+2）（x-2）＞0，再根据有理数的乘法法则“两数相乘，同号得正”，得到式子x+2>0，x-2>0或x+2<0，x-2<0，这样就将超纲问题转化为学生可解问题，这种解一元二次不等式的过程，真正体现了数学的化归思想.

2.3化归思想在函数探究问题中的应用

在一些函数问题上也经常用到化归思想，将不好把握的问题转化为容易理解的问题进行处理，如函数与方程或不等式之间的关系，借助图形将问题转化，解答轻而易举.［5］具体案例如下.

例3在平面直角坐标系xOy中，已知抛物线y＝ax2+bx经过A（4，0），B（1，4）两点.P是抛物线上一点，且在直线AB的上方.如图5所示，OP交AB于点C，PD∥BO交AB于点D.记△CDP，△CPB，△CBO的面积分别为S1，S2，S3.判断S1S2+S2S3是否存在最大值.若存在，求出最大值；若不存在，请说明理由.

针对S1S2+S2S3是否存在最大值的问题，学生很难直接入手，但如果将面积问题转化为线段之间的关系问题，学生就容易理解.如图6所示，根据PD∥OB，可得△DPC∽△BOC，所以CP∶CO＝CD∶CB＝PD∶OB，从而发现S1S2=CDCB=PDOB，S2S3=CPCO=PDOB，此时发现S1S2+S2S3＝2PDOB，这样只要再计算2PDOB的最大值即可将问题解决.

2.4化归思想在三角函数问题中的应用

在三角函数的相关内容学习时，也常常出现角与边之间的关系，利用化归思想，很容易突破边角关系，建立等式让问题得解.具体案例如下.

例4某市要举办首届旅游发展大会，该市积极优化环境.如图7所示，规划中的一片三角形区域需美化，已知∠A＝67°，∠B＝53°，AC＝80米，求这片区域的面积.（结果保留根号.参考数据：sin53°≈0.8，sin67°≈0.9）

根据题目的条件，学生无法进行正常计算，但是考虑到问题涉及三角函数，需要进行添加辅助线，构造直角三角形.在△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，如图8所示，过点C作CD⊥AB于点D，则在Rt△BCD中，CD＝asinB，在Rt△ACD中，CD＝bsinA，∴asinB＝bsinA，可得asinA＝bsinB，据此，可以转化得到三角形三边与三角函数值的关系，从而借助上述关系求得

AE，BC的值，即可得到S△ABC的大小，问题得以解决.

2.5化归思想在几何证明过程中的应用以人教版《义务教育教科书数学九年级上册》中关于“圆”部分内容为例，在研究分析“同弧所对的圆周角的度数等于这条弧所对的圆心角的度数的一半”的过程中，将问题分为三种情况：①当点O的位置在圆周角的一条边上（如图9）；

②在圆周角的内部（如图10）；③在圆周角的外部（如图11）.

教材根据第一种情况可以利用外角性质直接得到答案，但是对于后面两种情况，却要求学生自己研究解决.

面对这样的问题，很多同学在分析时找不到思路，其实是忽略了化归思想的运用，既然第一种方法如此简单，就可以将第二种、第三种情况分别转化为第一种问题的模式上来，从而连接点C与点O，形成直径，再利用第一种情况的解法顺利解答.

在几何图形求解阴影面积等方面，化归思想也经常体现其中.具体案例如下.

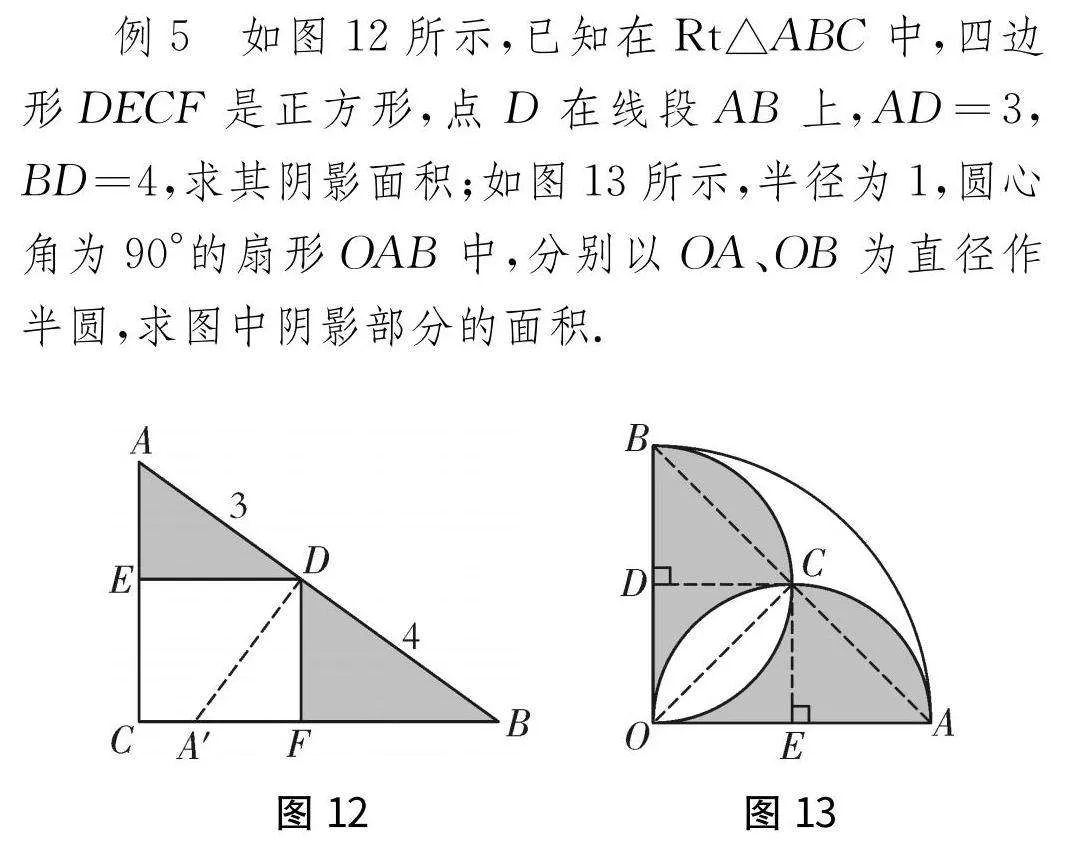
例5如图12所示，已知在Rt△ABC中，四边形DECF是正方形，点D在线段AB上，AD=3，BD=4，求其阴影面积；如图13所示，半径为1，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，求图中阴影部分的面积.

像这样的阴影面积问题，学生直接去求各个部分的面积往往计算量大或者繁琐，但是

在问题的特点基础上可以利用化归思想，将不规则的图形转化为规则的图形，解起来就非常简单，如图12中可以添加DA′这样一条辅助线，通过旋转将两个直角三角形转化为一个直角三角形即可求解.扇形问题通过分割将不规则的扇形填补形成一个等腰直角三角形，问题也很容易求解.

当然，在研究其他类型的几何图形证明过程中，同样可以借助题干中的情境进行转化，将问题转化为图形或者思维导图等方式进行解答，这样的化归思想能够将问题直观化.思路显性化，很容易找到问题的突破.

3结语

综上所述，化归思想在初中数学解题中有重要意义，把握化归思想的本质特点，善于从问题的情境中获取相关信息，进行等价转化，从而很容易将疑难问题化解.

［5］有了这种思想可以减轻学生对数学难题的恐惧感，也能轻而易举地找到问题的突破口随着新课程标准的实施，数学问题也不断向思维深度发展，教师在教学过程中更要注意化归思想的灌输与引导，让学生充分地把握其内涵，并在训练中灵活运用，从而达到提高数学思维能力，提升数学核心素养的最终目的.

参考文献

［1］秦艳萍.化归思想在三角函数解题中的应用［J］.数理天地（高中版），2022（15）：64-65.

［2］颜艳.渗透转化与化归思想 培养数学核心素养［J］.考试周刊，2021（78）：85-87.

［3］聂佑林.把握数学本质，重视化归渗透［J］.中学数学教学参考，2021（31）：50-52.

［4］王赛楠.转化思想在初中数学解题中的具体应用［J］.初中数学教与学，2022（7）：22-23+47.

［5］王学信.化归思想在初中数学教学中的渗透研究［J］.课程教育研究，2018（17）：156.