深度学习视域下初中数学单元教学设计

摘要：本文以深度学习为视角，将苏科版教材中的“用一次函数解决问题”“一次函数与二元一次方程”及“一次函数、一元一次方程和一元一次不等式”三部分内容整合为一个教学单元，即“一次函数的应用”.同时，将单元教学方法引入初中数学课堂，探讨在深度学习视域下的初中数学单元教学设计.通过确立着眼于数学核心内容的单元教学主题，明确指向数学学科本质的单元教学目标，组织恰当的教学内容和课时安排，创新多样化的教学方法和活动体验，设计体现深度学习的教学评价与反馈等单元教学设计路径，以提升学生的数学核心素养和深度学习能力.

关键词：深度学习；初中数学；单元教学设计

《义务教育数学课程标准（2022年版）》（以下简称“课程标准”）明确指出：“改变过于注重以课时为单位的教学设计，推进单元整体教学设计.”［1］通过多个课时的单元教学，教师带领学生深度参与学习过程，是实现深度学习、体现数学学科核心素养的育人价值的重要路径.同时，深度学习是以高阶思维为认知手段的高投入性学习，这就需要教师进行数学单元教学的整体设计，帮助学生发展理性思维，提升数学学习能力.

1深度学习视域下初中数学单元教学的内涵

1.1深度学习

深度学习是一种强调学生对知识的深层理解和灵活运用，促进学生的批判性思维和问题解决能力发展的学习方式.它不仅关注知识的传授，更注重学习过程中的探究和反思.深度学习的特点在于深度性、复杂性和关联性.深度性指的是学生对知识的理解和应用程度，复杂性则体现在学生需要运用多种思维方式和技能来解决问题，关联性则要求学生能够将不同领域的知识进行融合，形成完整的知识体系.

在数学教学中，深度学习的应用尤为重要.数学作为一门基础学科，需要学生具备扎实的数学基础以及高阶思维.着眼于深度学习，学生从数学研究的逻辑起点出发，通过构建多样的学习路径，如类比思想、化归思想、建模思想等，加深对数学概念、原理的理解，提高数学核心素养和解决问题的能力.例如，在学习代数方程时，学生不仅需要掌握方程的解法，还需要理解方程背后的数学原理和应用场景，这样才能更好地运用方程解决实际问题.

1.2单元教学

单元教学是一种将课程内容以单元的形式组织并实施教学的模式，旨在通过系统的教学设计，对教学内容的合理划分和统筹安排，使每个单元内的知识点能够相互联系、循序渐进地展开.单元教学强调知识体系的整体性和连贯性，教师通过一个个相对独立但又相互关联的单元教学，帮助学生在理解和掌握具体知识的同时，形成对学科内容的全面认识和深刻理解，有效提升学习效率.

1.3单元教学设计

单元教学设计是指在单元教学模式下，以整体思维为基础，根据教学目标、学生特点和学科内容，对相关教材内容进行统筹重组和优化，然后制定具体的教学计划和方案.设计过程中，需要明确每个单元的教学主题和目标，合理安排教学内容和课时，选择适当的教学方法和活动，制定科学的评价与反馈机制.单元教学设计的核心在于通过系统化和科学化的设计，确保教学目标的实现和学生学习效果的提升.一个成功的单元教学设计不仅要关注知识的传授，更要重视学生在学习过程中的探究、体验，以及综合素养的全面发展.

2深度学习视域下初中数学单元教学案例设计

2.1确立着眼于数学核心内容的单元教学主题

确立单元教学主题是单元教学设计的第一步，也是最关键的一步.教学主题应着眼于数学学科的核心内容，选取学科体系中具有基础性、关键性和综合性的知识点作为教学重点.例如，在初中数学中，一元一次方程、一元一次不等式和一次函数等内容不仅是学科的基础知识，同时也是学生今后学习其他数学内容的重要前提.在确立教学主题时，应充分考虑这些内容的内在联系和学生的认知水平，通过情境问题的引入和探究活动的设计，使学生在解决问题的过程中逐步理解和掌握这些核心概念，培养学生数学思维和解决问题的能力.

2.2明确指向数学学科本质的单元教学目标

单元教学目标的确定应以数学学科的本质为导向，明确指向学生数学核心素养的提升.［2］数学学科的核心素养包括数感、符号感、空间观念、几何直观和数据分析观念等.这些素养不仅是学生理解和应用数学知识的基础，也是其今后进行数学学习和实际应用的重要能力.单元教学目标应具体、明确、可测量，并与学生的实际情况相适应，同时能在学习过程中促进学生思维能力和数学素养的提升.

2.3组织恰当的单元教学内容和课时安排

教学内容的组织应基于学生的认知规律和学习需求，课时安排要合理，既要保证内容的完整性，又要留有足够的时间让学生进行探究和反思.

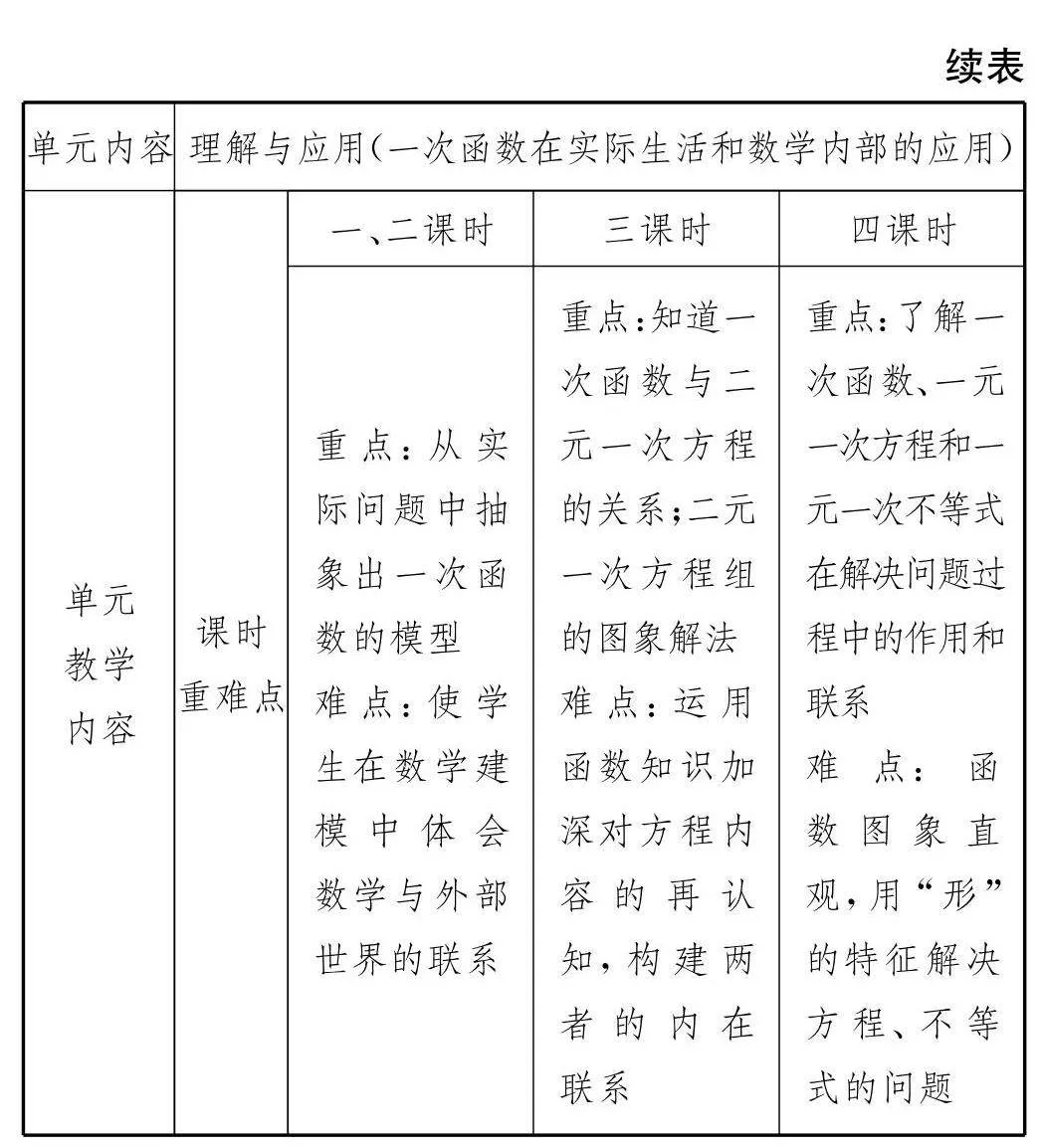
例如，在教学苏科版《义务教育教科书数学八年级上册》中《一次函数》时，可以将本章内容划分为“基本概念”“图象与性质”“理解与应用”“数学活动与体验”等4个学习单元12个课时.在开展“理解与应用”单元教学时，主要涵盖的内容有“用一次函数解决问题”“一次函数与二元一次方程”以及“一次函数、一元一次方程和一元一次不等式”三部分.一次函数在实际生活和数学内部的应用两部分可以设置成4个教学课时.通过将章节内容科学合理地划分并组合成单元教学内容，使学生更加了解每个单元的教学内容，不仅能有效提高学生的认知水平，还能够深入挖掘单元教学内容隐藏的数学基本思想及学习方式，突出该单元教学内容的核心素养，如数学建模、逻辑推理与运算、直观想象等方面，帮助学生实现深度学习初中数学知识内容.

以“理解与应用”单元为例，笔者设计了单元教学目标、单元教学内容，单元教学内容又包括了课时内容、课时目标及课时重难点（见表1）.

2.4创新多样化的数学教学方法和活动体验

“活动与体验”是单元教学中不可或缺的组成部分，是深度学习的核心特征.教师可以通过多样化的教学活动和丰富的学习体验，激发学生的学习兴趣，提升其参与度和主动性.［3］活动的设计应紧扣教学目标和内容，既要有助于学生知识的理解和技能的掌握，又要注重学生能力的发展和素养的提升.例如，教师可以设计小组合作学习、探究式学习、项目式学习等多种形式的活动，鼓励学生通过讨论、实验、实践等方式进行深度学习.此外，教师还可以组织数学游戏、数学竞赛、课外调研等活动，增加学生学习的趣味性和实用性，使学生在轻松愉快的氛围中进行学习和思考，真正做到学以致用.

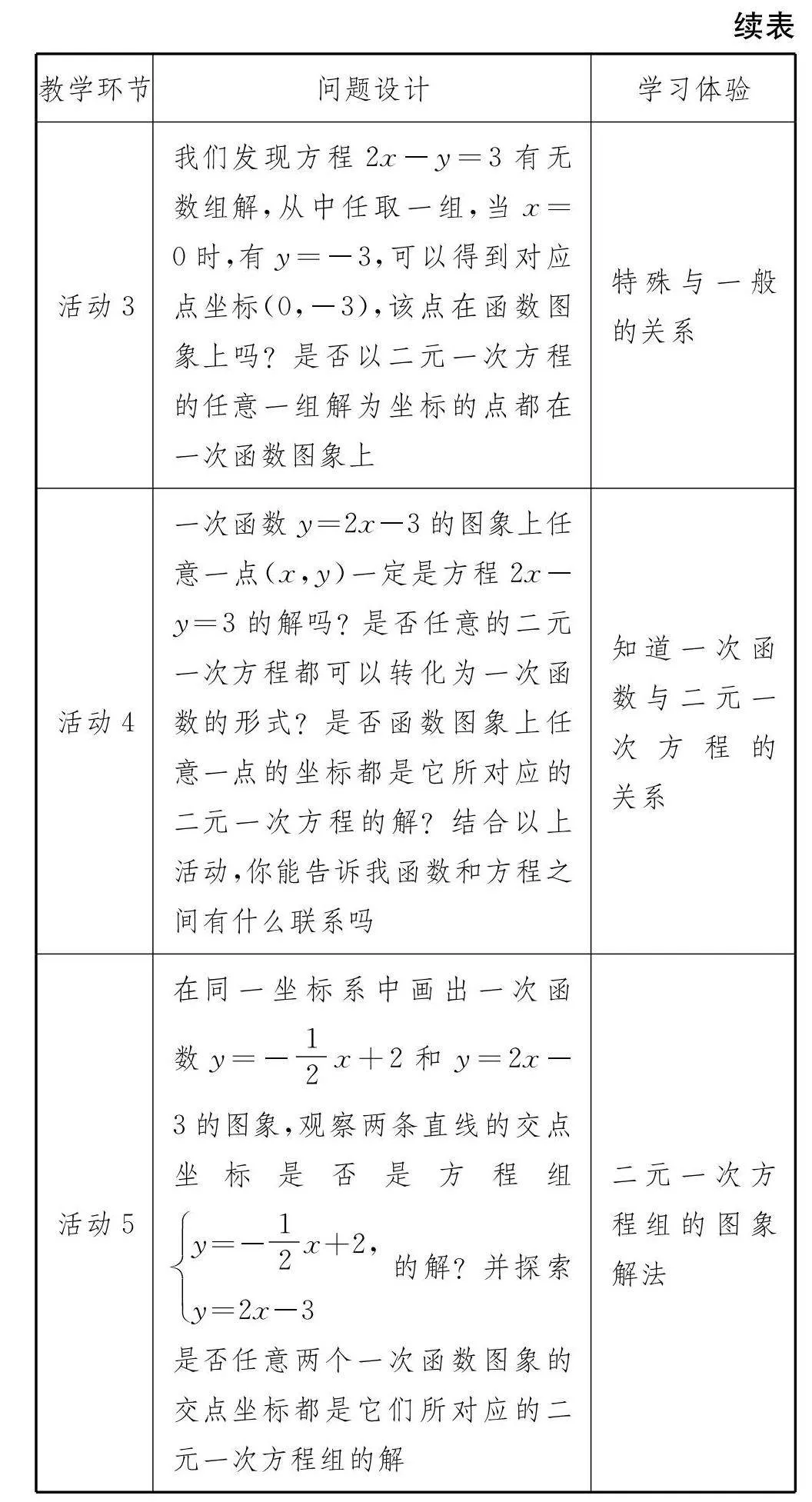
以“理解与应用”单元的第三课时“一次函数与二元一次方程”为例，设计如表2所示的学习单.

2.5设计体现深度学习的教学评价与反馈

在深度学习视域下，教学评价与反馈不仅是对学生学习成果的检验，更是促进学生持续改进和发展的重要手段.设计体现深度学习的教学评价与反馈，应包括多元化的评价方式（形成性评价，终结性评价，注重过程性评价）、及时有效的反馈机制，以便对评价结果的合理运用，从而全面了解和提升学生的学习质量.

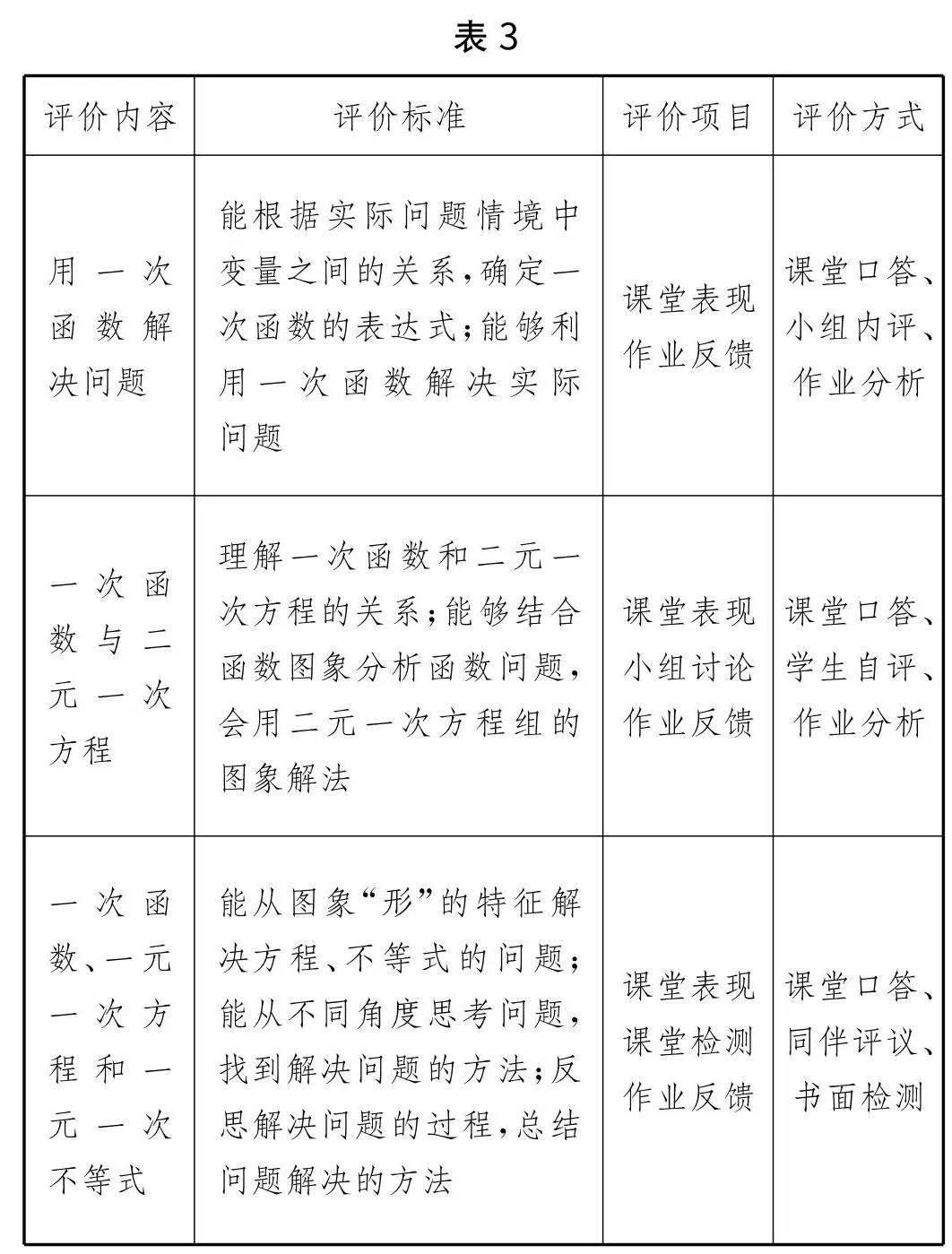
以“理解与应用”单元为例，通过课堂观察、随堂测验、作业检查、小组讨论等方式进行形成性评价；通过阶段性测试、单元考试、项目报告等方式进行终结性评价；通过学习日志、反思报告、同伴评议等方式进行自评与互评；通过口头反馈、板书提示、个别指导等方式进行即时反馈等.及时有效的反馈机制和对评价结果的合理运用，可以全面了解学生的学习情况，及时发现和解决学生学习中的问题，促进学生的持续改进和全面发展.评价与反馈不仅是对学生学习成果的检验，更是引导学生深度学习、提升核心素养的重要手段.以“一次函数的应用”为例，设计如表3所示的单元评价表.

3反思与优化教学设计

3.1提升活动与体验任务的探究性和开放性

提升活动与任务的探究性和开放性是促进学生深度学习的重要途径.探究性任务旨在引导学生通过自主探究、独立思考，发现问题，解决问题，从而培养学生的创新思维和实践能力.开放性任务则鼓励学生从多角度、多层次进行思考和探索，不必拘泥于固定的答案和模式.在教学设计中，教师通过探究性和开放性任务的设置，帮助学生在“问题情境—分析问题—建立模型—求解验证”的数学学习活动过程中进行自主学习和合作学习.［4］同时为学生提供多样化的学习资源和工具，支持学生进行个性化的活动与体验.

以学习 “理解与应用”单元的第四课时为例.

活动1：通过4个学习任务进行实践、讨论，引导学生探究、总结出一次函数与一元一次方程之间的联系.其中，任务1为在平面直角坐标系中作出一次函数y=2x+4的图象；任务2为观察图象，找出图象与x轴交点的横坐标；任务3为求方程2x+4=0的解；任务4为讨论图象与方程的解之间的联系.

这样的活动任务具有开放性，有利于学生通过活动与体验来探究并解决问题，提升数学学科思维水平和核心素养.［5］

活动2：画出函数y=-2x+1的图象，观察图象并完成学习任务.

x取何值时，y=0？x取何值时，y＞0？ x取何值时，y＜0？

观察图象，学生发现一次函数与一元一次方程、一元一次不等式之间有密切的联系，当一次函数值等于0时为一元一次方程，当一次函数值大于或小于0时为一元一次不等式.通过层层深入的探究，有利于学生形成逻辑更加清晰和完整的思维过程.同时，教师可以依据学生对以上问题的回答对他们进行思维结构评价.［6］

3.2掌握正确的单元教学评价与反馈方法

深度学习强调评价时强调全面性和反馈的及时性.在进行教学评价时，教师应关注学生的学习过程和学习结果，通过课堂观察、学生自评与互评、作业分析等多元化的评价手段，全面了解学生的学习情况，并准确地为学生提供个性化的反馈.教师还应根据评价结果及时调整课堂教学行为和策略，实现“教学评一致性”.同时，教师要加强对教学评价数据的挖掘，这样可以让学生充分了解自己的深度学习情况，便于及时调整学习策略.对此，教师应掌握正确的收集和处理学生信息的方法，不断探索和创新，完善评价与反馈机制，提升教学质量，为促进学生的深度学习提供有力保障.

参考文献

［1］唐彩斌，史宁中.素养立意的数学课程——《义务教育数学课程标准（2022年版）》解读［J］.全球教育展望，2022（6）：24-33.

［2］马云鹏.《义务教育数学课程标准（2022年版）》的理念与目标解读［J］.天津师范大学学报（基础教育版），2022（5）：1-6.

［3］孔凡哲，史宁中.《义务教育数学课程标准（2022年版）》教学活动标准解读［J］.天津师范大学学报（基础教育版），2022（6）：21-25.

［4］王远敏，杨川.指向单元整体的课时教学设计研究——以“有理数的减法”为例［J］.中学教学参考，2022（35）：7-9.

［5］钟菊红.九年级主题式单元复习课的教学设计与实践——以“图形运动”单元为例［J］.中国数学教育（初中版），2023（23）：31-36.

［6］崔允漷.试论新课标对学习评价目标与路径的建构［J］.中国教育学刊，2022（7）：65-70+78.