学科“美融”的理论与实践探索

摘要：美是纯洁道德、丰富精神的重要源泉.学校作为对学生进行美育的主要教育地，把美育纳入了各级各类学校人才培养中，在此基础上的特色发展也可以加强各学科之间的有机融合.本文以高中数学学科“美融”的理论学习和实践探索作为探讨的大标题，以数学学习软件GeoGebra在高中数学中的教学以及在数学美育中的运用作为主要内容，通过GeoGebra软件在高中数学教学中的应用，在美育教学的指导下，帮助学生更好地学习高中数学知识以及提高学生在高中数学学习中的兴趣并开拓学生的创造力和思维学习能力.

关键词：学科“美融”；高中数学；GeoGebra软件

本文的研究背景是基于学科“美融”的理论基础，考虑高中数学教学课堂的实际情况，结合新课程标准的要求，阐述数学学科与GeoGebra软件（以下简称“GGB”）教学“美融”的内容和方法，尝试培养学生数学学习兴趣和能力.本文将采用文献研究法、实践探索分析法和归纳总结法等方法，开展GGB在高中数学教学中的应用问题研究.具体从学科“美融”理论的含义、高中数学与GGB软件应用“美融”特征、GGB软件在高中数学教学中的应用案例研究等几个方面展开，通过对相关GGB软件在数学教学中的案例研究进行思考总结，结合新课程标准提出关于高中数学教学学科“美融”的GGB应用推广的针对性建议.

1学科“美融”理论的含义

美育又被称为美感教育或者审美教育，如何在高中数学教学中深入践行美感教育是一门必修课.一方面，高中数学的美感教育需要与学科特色相互融合，才能发挥出美感教育在培养学生对高中数学学习的兴趣以及培养学生创新能力上的优势；另一方面，美育是以情动人的美的教育，是通过对美的形象的情感渲染来传递相关知识.因此，如何在高中数学教学中寻找美感教育和传统教育的平衡点是需要深入研究的.［1］

学科“美融”理论是指在相关学科教学过程中融合美学教育，帮助学生完成从学科实践能力的培养，到最终实现人的和谐、自由的发展，实现人的丰富性.学科“美融”的落实可以从育人目的、实施过程、实施效果三个方面进行探讨.在高中数学的学科“美融”的实践探索中，

GGB软件的实践内容是指该软件通过创造出和谐的美的数学知识点帮助高中数学学科教学创造良好的学习氛围.［2］本文重点研究和讨论的内容是目前数学学习软件GGB在教学中的应用而创造出的较为和谐的数学学科“美融”实践探索的现状.

2高中数学与GGB软件应用“美融”特征

通过对学科“美融”理论的理解以及美育理论的学习，可以发现学科“美融”具有趣味性、感染性和多样性等特征.与德育和智育的特点不同，美育的学科融合需要展现的形象是生动、活泼、有趣，这也是美育本身的特点.GGB软件是一款用于大中小学数学教与学的免费开源软件，主要内容包括代数区、绘图区、3D绘图区、表格区等，其中代数区除了可以进行数值计算，还可以进行符号运算.目前在高中数学教学中，绘图区的应用比较多.绘图区可以做出各种平面几何图形或函数图象，绘制出的图象非常适合高中数学课堂的教学.

高中数学与GGB软件“美融”的生动性体现在应用GGB软件较为强大的功能性，可以创造出美观且具有实用性的49278ef058626c24f3043de13853be1b具体图象或者生成相关表达式图象，这个过程是数学学习软件与高中数学“生动性”最大的体现.以苏教版《普通高中教科书数学必修第一册》中第六章《幂函数、指数函数和对数函数》这一部分内容为例，书本上出现的图象就是利用数学学习软件GGB生成的.在这部分内容学习中，一方面，学生可以通过生成的图象对函数的相关性质有一个较为清晰的理解.以幂函数为例，学生可以通过对相关图象的观察分析，发现函数图象经过的定点、函数的单调性以及其他相关性质.另一方面，在利用GGB软件生成函数图象的过程中，可进一步深化学生对函数性质的理解和掌握.

高中数学与GGB软件“美融”的感染性体现在相对于传统的数学课堂教学的讲授法，GGB软件教学会给学生创造自主参与函数或表达式图象的生成过程的机会，学生参与度会比较高，这样也就体现出高中数学与GGB软件“美融”的感染性.

高中数学与GGB软件“美融”的多样性主要体现在基于目前学习函数的类别，GGB软件产出的图象类别会相对较多，并且随着相关图形知识点的扩充，GGB高中数学图象库也会随之扩充，这也是高中数学与GGB软件“美融”的多样性体现.

3高中数学与GGB软件应用“美融”的实例分析

高中数学与GGB软件应用“美融”的实例是比较多的，而且高中的每本课本都有可以应用GGB软件的课程内容.本文将介绍GGB软件在高中数学教学中“美融”的两个例子，具体如下.

3.1GGB软件在指数函数和对数函数中的应用

学生在没有了解过GGB软件的背景情况下，对于GGB软件的认识会较为深刻.同时课堂上GGB软件的数字化教学也是学生培养数学学习兴趣，提高GGB软件应用学习的最佳时机.

以指数函数和对数函数中GGB软件的应用为例.基于课本教学指导以及课下讨论，在这一部分的GGB软件教学中，重点并没有放在相关图象的生成过程上，而是偏向于GGB软件初次使用的介绍以及辅助学生对相关函数性质的分析理解.

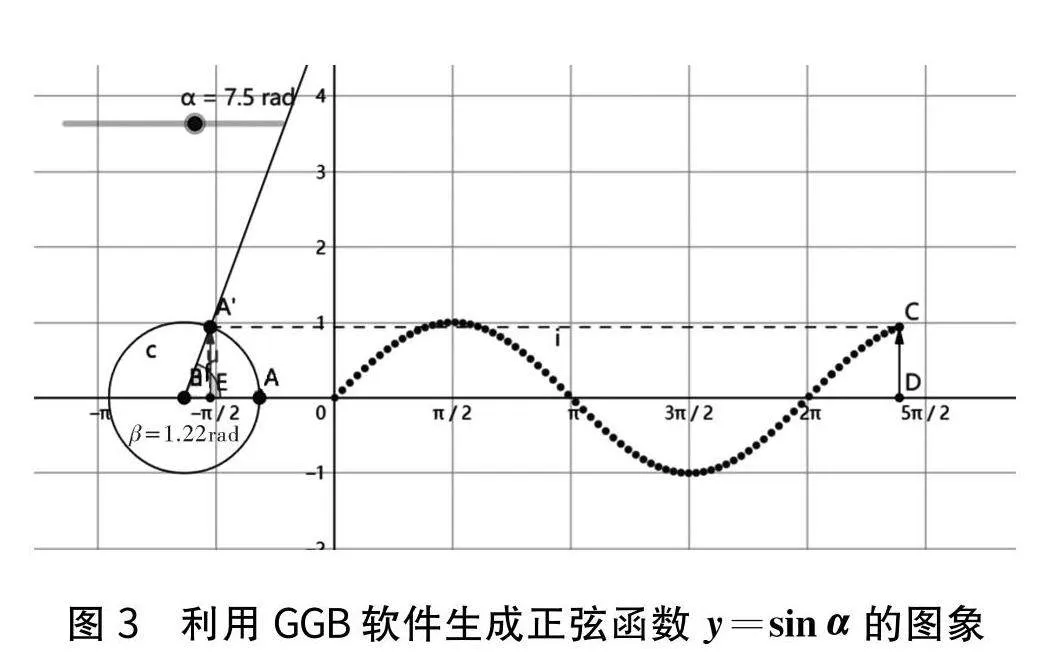
如图1所示，GGB软件生成的函数图象非常直观且具有对称美，并且体现了指数函数图象的相关特点和性质.回归到图象中的指数函数，通过直观观察可以发现指数函数过一个定点（0，1），并且指数函数具有一定的对称性，即f（x）=ax（a>0且a≠1）与g（x）=1ax（a＞0且a≠1）图象关于y轴对称.通过更深一层的探究可以发现，指数函数的单调性与函数解析式中a的取值有一定的联系.当a>1时，函数f（x）=ax（a>0且a≠1）单调递增;当a<1时，函数f（x）=ax（a>0且a≠1）单调递减.上述指数函数相关性质的总结可以先对GGB软件生成的函数图象进行观察，再让学生通过自己的操作去验证这些结论是否具有一般性，最后再在老师的指导下进行结论的证明.通过上述完整的学习过程，学生会对这部分知识点产生较为深刻的认识和理解.

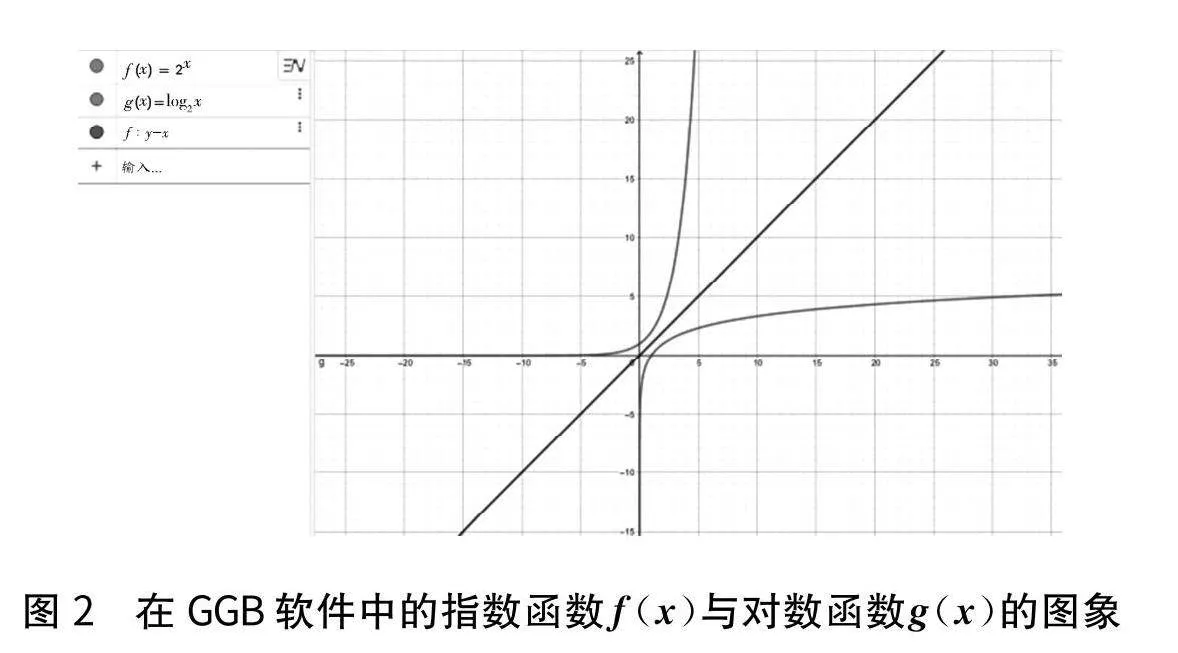
当然，在单独学完指数函数和对数函数的图象和性质后，把指数函数和对数函数图象放置在同一个GGB软件中，又可以有新的发现，即相同底的指数函数f（x）=ax（a>0且a≠1）和对数函数g（x）=logax（a>0且a≠1）关于函数y=x对称，如图2所示.

3.2GGB软件在画出三角函数图象中的应用

在画出三角函数图象前，根据苏教版书本中的课程教学顺序，三角函数线的学习是相对靠前的，也就是说在书本教学画出三角函数图象前，学生已经较为充分地理解了三角函数线的概念以及相关做法.在这里应用GGB软件生成三角函数图象可以帮助学生对相关函数图象的生成有一个更为深刻的理解.

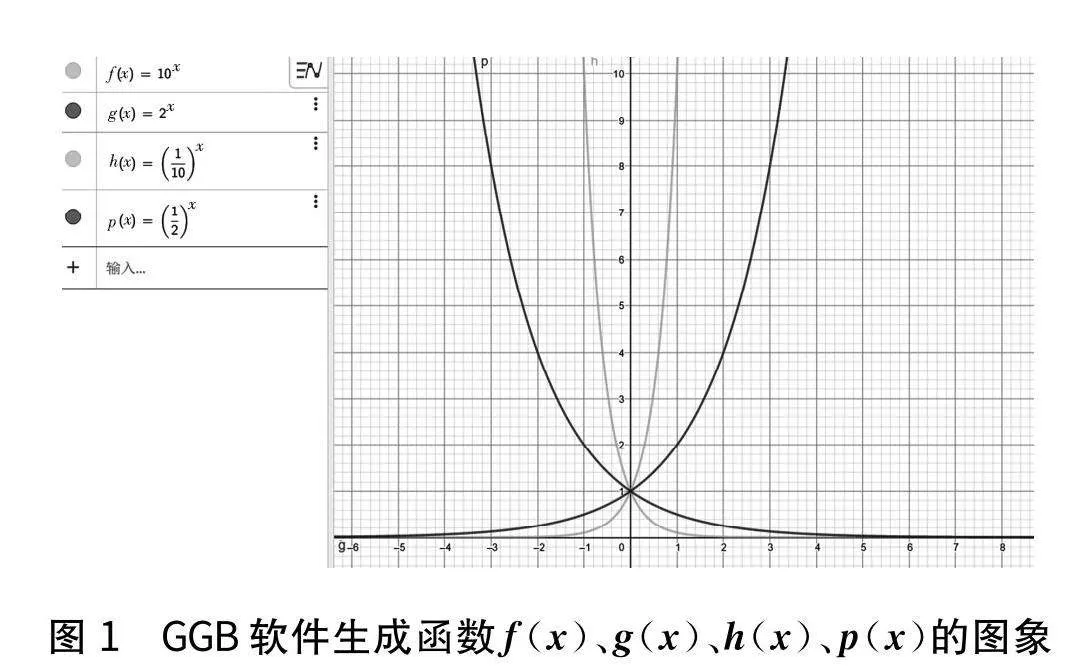
在课堂上，教师会向学生展示利用三角函数线画出三角函数图象的动态生成过程，这充分体现了GGB软件与高中数学“美融”的生动性、感染性和多样性.在展现之后，教师可以引导学生在课下利用计算机使用GGB软件完成相关三角函数图象的动态生成.同时，在学校开设相关的数学校本课程上也可以增设GGB软件的应用.学生既可以提前预习这部分知识点，也可以在这类课堂上专门练习这部分知识点，从而起到培养学生对数学学习兴趣和动手创造能力的作用.以生成正弦函数图象为例，图象如图3所示.

4高中数学与GGB软件应用“美融”存在的问题和未来展望

GGB软件在高中数学教学中有着重大意义，不仅对学生对于知识点的理解掌握具有较高的辅助性，而且也能培养学生动手创造能力以及对数学学习的兴趣.这是学科“美融”的生动展现，但是目前GGB软件的应用仍具有一定的局限性.

首先，GGB软件虽然对于新手的要求不是非常高，但是GGB软件应用技能是需要教师去提前学习的.那么，是自学还是组织统一教学，怎么组织统一教学，由谁来主导教师学习GGB软件，这些都是目前面临的问题.当然，在教学之前，学校需要拥有较为完整且顺畅安装相关软件的流程.

在上述条件允许的基础上，GGB软件的学习在青年教师队伍中是便于推广的，目前部分高校是有设计相关教学软件的教学课程，其中包括几何画板以及数学学习软件GGB的应用学习.将高校学习的内容渗透到高中数学教学中，难度以及内容都是向下兼容的，既可以达到高中数学与GGB软件应用“美融”的结合，又可以为学生创造较大的成长空间.

本研究的主要结论如下.

（1）GGB软件在高中数学教学中的应用目前还处于实验推广阶段，相关软件的推广以及应用学习对于部分学校而言具有一定的难度.

（2）GGB软件在高中数学教学中的应用是数学学科和计算机学科的“美学教育融合”，对于部分高中数学知识点，利用软件教学更有利于学生对该知识点的理解学习以及掌握.

（3）在条件允许的基础上，GGB软件的学习在青年教师队伍中是便于推广的，并且在新时代发展的潮流下，相关软件的学习教程也是相对便捷的.

GGB软件在高中数学教学中的应用目前还处于实验推广阶段，每一个实验效果的完善或者是新的实验操作产生对于学科“美融”来说都是一个进步，也是帮助学生更好地学习高中数学知识以及培养学生创造能力的基石！

参考文献

［1］曾永成.美学原理［M］.成都：电子科技大学出版社，1999.

［2］彭锋.美学的意蕴［M］.北京：中国人民大学出版社，2001.