数学建模思想融入高中函数模型教学的实证研究

摘要：随着新课程改革的不断深入，数学建模思想，特别是函数模型思想，作为一种重要的数学思想，已逐渐融入高中数学教学之中.受到诸多外部因素影响，数学建模思想并未广泛应用于高中数学教学活动，这使得数学建模思想优势难以体现.鉴于此，教师依托新课标积极开展高中函数模型教学活动，凸显数学建模思想的重要作用，致力于为高中函数教学注入新鲜血液，促进数学建模思想的推广应用，为提高高中生解决数学问题能力提供有效手段.

关键词：高中数学；数学建模思想；函数模型教学；教学设计

函数模型是数学的重要分支，也是高中数学教学的核心内容之一.在传统的高中函数模型教学中，教师过于注重公式和定理的灌输，忽视了学生数学建模能力的培养.随着《普通高中数学课程标准（2017年版2020年修订）》（以下简称“新课标”）的颁布，数学建模作为一种重要的教学方法已逐渐融入高中数学教学之中.［1］本文旨在通过实证研究，探讨和分析数学建模思想融入高中函数模型教学的效果和影响，增强学生实践能力.

1函数模型教学设计

1.1教材分析

函数作为高中数学知识体系的重要组成内容，贯穿于高中数学教学始终.函数知识是数学学习的重点和难点内容之一，对学生数学学习能力要求较高.其中，指数函数是最基本且最具代表性的函数，是帮助学生打好函数学习基础的重要学习内容.因此，在指数函数学习中，有必要引入函数模型教学手段，加强对函数的研究与解决，增强学生函数学习技能.

《指数函数的性质与图象》是人教B版《普通高中教科书数学必修第二册》中的内容，这一知识点的学习是在学生已学习过函数概念与性质、实数指数幂及运算等知识点的基础上，对指数函数的概念、性质、图象等进行系统性学习，为学生综合性发展提供重要依据.教师在指数函数性质与图象教学中，能够增强学生对函数图象、代数运算方法的应用能力，使学生在探索函数性质的基础上建构函数模型思维，阐明数学建模思想的重要作用，为学生形成数学学科核心素养提供有效路径.

1.2学情分析

教师在开始函数模型的教学设计之前，需要对学生的情况进行分析.根据新课标的要求，学生已经掌握了一定程度的基础函数知识，包括代数、几何和初中阶段的函数概念.然而，学生在函数模型的理解和应用上仍存在一定困难，尤其是在将实际问题转化为函数模型的能力上.因此，教师在教学设计中需要考虑如何帮助学生建立函数模型的概念，提高他们应用函数模型解决实际问题的能力.

从知识基础层面分析，学生已具备函数概念知识素养，能够通过数学语言、数学方法了解他们在学习过程中遇到的问题和困难，以及他们对数学建模思想的认识和接受程度.

从认知能力层面分析，学生在理解知识点时存在认知偏差，不利于提高对知识点的分析与解读能力.通过本节课教学，教师以指数函数的性质与图象的问题解决，激发学生对函数知识点的求知欲，提高学生的函数学习综合能力.

1.3教学目标

本节课的教学目标如下.

（1）知识与技能目标：让学生理解函数模型的概念，掌握函数模型的基本性质和特点.

（2）过程与方法目标：培养学生将实际问题转化为函数模型的能力，提高他们应用函数模型解决实际问题的能力.在研究指数函数y=2x 和y=12x的图象和性质后，增强学生的高阶思维能力，发展数学建模思想.

（3）情感态度与价值观目标：培养学生通过数学语言和符号表达函数模型的能力，提高他们的数学表达能力，使其在进阶思维转化中培养数学建模思想，为学生强化数学学习能力提供重要依据.

1.4教学重难点

本节课的教学重难点如下.

（1）教学重点：培养学生的数学建模能力，引导学生了解函数模型的概念和基本性质.

（2）教学难点：帮助学生掌握将实际问题转化为函数模型的方法和技巧，培养学生应用函数模型解决实际问题的能力.

1.5教法分析

通过将数学建模思想融入高中函数模型教学的效果，笔者发现结合数学建模的教学策略可以有效提高高中函数教学的质量和学生的数学素养，激发学生的学习兴趣，调动学生主动学习意识，从而培养学生模型建构思维，提升学生主动建构模型的能力.［2］同时，探究指数函数知识点时，教师应体现以学生为主体的思想，为学生提供良好的学习环境，培养学生自主学习能力，促使学生具备深入思考、系统解读、小组合作、互动学习等综合能力.在讲解函数模型的概念时，通过具体的例子让学生理解函数模型的基本性质和特点，帮助学生建立函数模型的概念.

2函数模型的教学过程

2.1创设情境，导入新知

例1细胞经过分裂，1个分2个，2个分4个，4个分8个，以此类推. 1个细胞经过x 次分裂后，得到的细胞个数y 与分裂次数x 之间存在怎样的关系.

教师要求学生独立思考，再进行小组合作学习，最终获得学习结果.教师选择两个学习小组进行作答.

预设答案：第一次细胞分裂，个数为2，2=21；第二次细胞分裂，个数为4，4=22；第三次细胞分裂，个数为8，8=23，以此类推，第x次细胞分裂，个数为2x ，y=2x.

师：我们之前学习了哪些函数？它们有什么共同特点？

生1：我们学过一次函数、二次函数等，它们的共同特点是可以表示两个变量之间的关系.

师：这些函数在实际生活中有哪些应用？

生2：一次函数可以表示直线，应用于测量、建筑设计等；二次函数可以表示抛物线，应用于物理、工程等领域.

师：同学们总结得很好.今天我们将学习一种新的函数模型——指数函数.请大家认真观察指数函数的定义式y=ax（a为常数且a>0，a≠1）.

【设计意图】通过“细胞分裂”情境，引导学生思考如何用数学模型来描述实际问题，以此来激发学生的学习兴趣，提高学生的学习积极性.这样的情境教学很好地诠释了高中数学的跨学科价值，帮助学生感受数学在不同学科中的作用，锻炼学生将数学知识与其他学科紧密融合的能力，由此引导学生在实际问题中建构模型抽象思维，为导入指数函数相关知识点做好铺垫.

2.2自主探究，模型建立

教师引导学生总结指数函数的概念和性质.

（1）指数函数的解析式为y=ax（a为常数且a>0，a≠1）.

（2）指数函数的单调性：当a>1时，函数在定义域上单调递增；当0<a<1时，函数在定义域上单调递减.

（3）指数函数的图象特点：函数图象经过第一、二象限，过定点（0，1）.

师：请大家用几何画板验证一下指数函数的单调性.

学生自主探究，教师巡回指导.

生3：我发现，当a>1时，指数函数在定义域上单调递增；当0<a<1时，指数函数在定义域上单调递减.

师：非常好，同学们已经掌握了指数函数的基本性质.下面，我将举例说明指数函数在实际生活中的应用.

【设计意图】教师通过具体的例子讲解函数模型的概念，让学生理解函数模型的基本性质和特点，引导学生思考如何用数学模型来描述这些问题，并从中分析一些具体的实际问题，引导学生将问题转化为函数模型，并通过数学语言和符号表达出来.［3］

2.3总结性质，分析模型

教师总结：函数是数学中的一个重要概念，它们广泛应用于各个领域. 指数函数具有独特的性质和应用，让学生了解指数函数的基本形式y=ax（a为常数且a>0，a≠1）.

师：研究指数函数y=2x的性质，并绘制出它的函数图象.

教师通过提问的方式引导学生结合已学过的函数知识，如一次函数、二次函数等，绘制y=2x的图象.

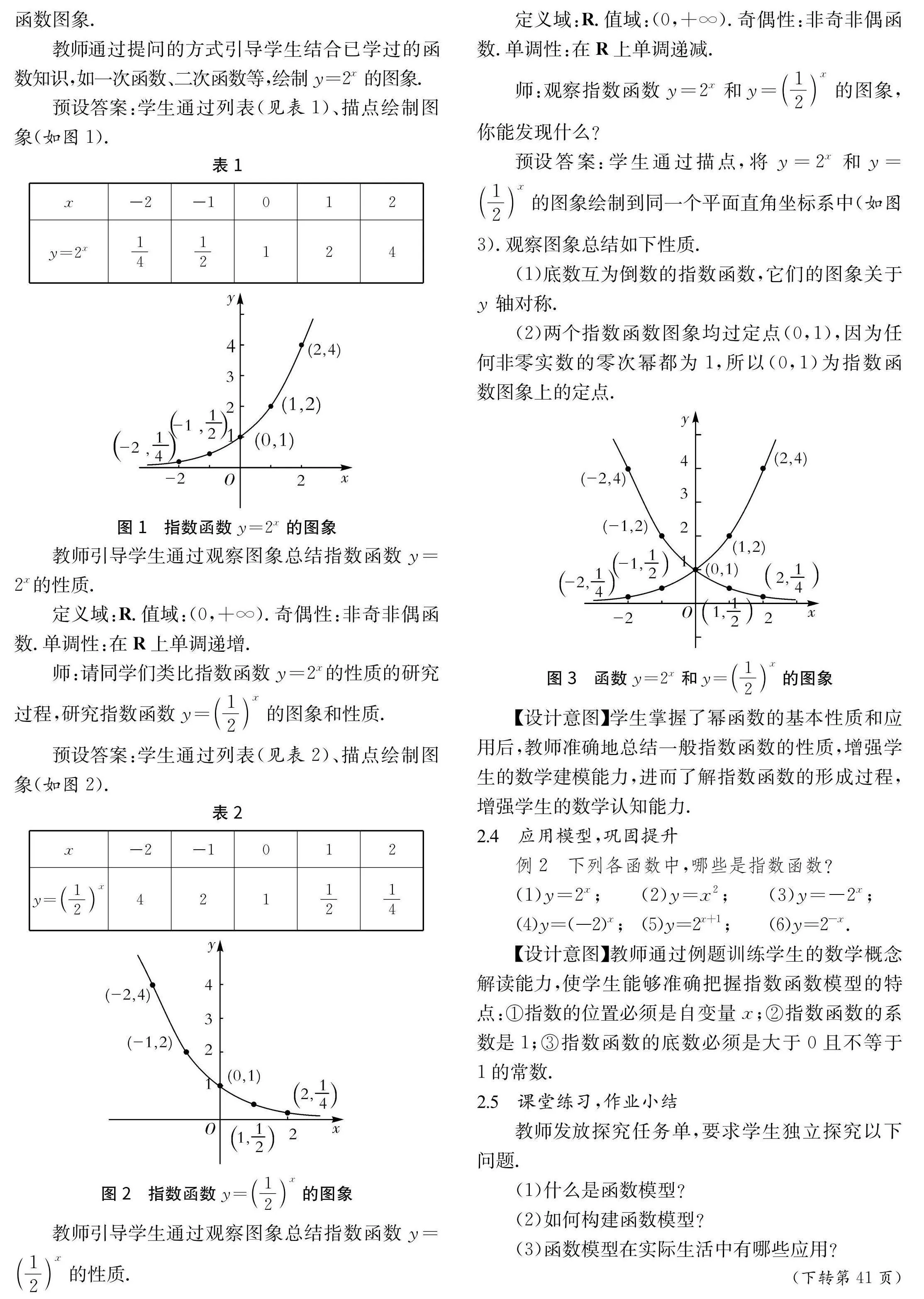
预设答案：学生通过列表（见表1）、描点绘制图象（如图1）.

教师引导学生通过观察图象总结指数函数y=2x 的性质.

定义域：R.值域：（0，+∞）.奇偶性：非奇非偶函数.单调性：在R上单调递增.

师：请同学们类比指数函数y=2x 的性质的研究过程，研究指数函数y=12x的图象和性质.

预设答案：学生通过列表（见表2）、描点绘制图象（如图2）.

教师引导学生通过观察图象总结指数函数y=12x的性质.

定义域：R.值域：（0，+∞）.奇偶性：非奇非偶函数.单调性：在R上单调递减.

师：观察指数函数y=2x和y=12x的图象，你能发现什么？

预设答案：学生通过描点，将y=2x和y=12x的图象绘制到同一个平面直角坐标系中（如图3）.观察图象总结如下性质.

（1）底数互为倒数的指数函数，它们的图象关于y 轴对称.

（2）两个指数函数图象均过定点（0，1），因为任何非零实数的零次幂都为1，所以（0，1）为指数函数图象上的定点.

【设计意图】学生掌握了幂函数的基本性质和应用后，教师准确地总结一般指数函数的性质，增强学生的数学建模能力，进而了解指数函数的形成过程，增强学生的数学认知能力.

2.4应用模型，巩固提升

例2下列各函数中，哪些是指数函数？

（1）y=2x；（2）y=x2；（3）y=-2x；

（4）y=（-2）x；（5）y=2x+1；（6）y=2-x.

【设计意图】教师通过例题训练学生的数学概念解读能力，使学生能够准确把握指数函数模型的特点：①指数的位置必须是自变量x；②指数函数的系数是1；③指数函数的底数必须是大于0且不等于1的常数.

2.5课堂练习，作业小结

教师发放探究任务单，要求学生独立探究以下问题.

（1）什么是函数模型？

（2）如何构建函数模型？

（3）函数模型在实际生活中有哪些应用？

生：函数模型是用来描述两个变量之间关系的数学模型，构建函数模型的方法有解析式法、图象法、表格法等.函数模型在实际生活中有广泛的应用，如线性规划、最优化问题、概率论等.

教师补充总结：函数模型是数学中的重要工具，它可以帮助我们更好地理解和解决实际问题.掌握函数模型的构建方法和应用技巧对于同学们今后的学习和工作都有很大帮助.

【设计意图】教师应用已学知识，培养学生的质疑能力，引导学生在解决实际问题中应用指数函数，增强学生构建函数模型的能力，深化开展对高中指数函数学习活动，切实提高学生的数学综合学习能力.

3结语

新课标背景下，高中数学建模思想的渗透能够提高数学课程教学质量与效率，能够提高学生实践学习综合能力，为培养高中生数学学科核心素养提供有利依据.高中数学建模思想贯穿到函数教学中，能够增强学生对知识点的分析、推理、讨论、实践等能力，促使学生在建模思想下提高综合学习能力，为学生综合性发展提供重要依据.在上述教学案例分析推理中，教师与学生建立有效沟通，了解学生对数学建模思想的认知情况，帮助学生通过自主学习过程，增强实践学习能力，进而掌握指数函数概念、性质、图象等知识点，彰显函数模型教学的有效性作用.

参考文献

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.

［2］刘天明.高中数学建模教学策略的实践研究——以三角函数模型为例［J］.数学之友，2022（22）：26-28.

［3］陈国鸿.模型思想视角下高中函数教学探究［J］.中学课程资源，2022（3）：9-11.