基于新课标的高中数学建模教学实践研究

摘要：开展数学建模活动对培养高中生数学核心素养具有促进作用，能够使学生将理论与实践紧密结合，使高中数学教学实现培育优秀人才的目标，与新课标教育理念紧密融合，培养高中生的数学关键能力.本文从新课标出发，论述数学建模教学思路的重要性，致力于提高数学课程教学质量与效率和培养高中生数学学科综合素养.

关键词：新课标；高中阶段；数学建模；教学实践

高中数学教学旨在从理论教学切入，发展学生实践能力.教师应以《普通高中数学课程标准（2017年版2020年修订）》（以下简称“新课标”）为依据，将数学建模思想融入教学活动，为高中数学建模教学提供实践平台，发展学生综合能力.［1］高中阶段是学生抽象思维进阶的关键期，对于提高学生数学抽象思维能力具有促进性作用.鉴于此，在高中数学教学中，教师应优化数学建模教学实践活动，体现学生本位思想，发展数学能力，全面培养学生实践学习能力.本文从数学实践活动视角出发，以“周期现象的描述”教学为例创设数学建模教学实践活动，以期提高学生数学建模素养和数学学习能力.

1“周期现象的描述”教学分析

1.1学情分析

（1）知识基础.“周期现象的描述”主要是对“函数”知识的教学.教师通过正弦函数、余弦函数、正切函数知识点的教学培养学生的函数模型思维，使学生能够在本课时学习中掌握重要知识点，初步建构数学模型思想.例如，在学习正弦函数与余弦函数知识点时，教师帮助学生了解数学模型在数学中的重要性，给予学生变式思维的启迪，深层剖析函数的关系，增强学生的函数建模能力，促zhiDt0QW/UYujuGJ4g/xG4BhZGkHKYWyXbKnfJ+ZJ58=进学生数学建模思想发展.［1］高中数学建模学习分为三个阶段：第一阶段，设在人教B版《普通高中教科书数学必修第一册

》中，学生初识数学建模思想，初步掌握模型思维的形成路径和方法，掌握报告撰写的技巧；第二阶段，设在人教B版《普通高中教科书数学必修第二册》中，在教师的指导下，学生能够了解建模的应用路径和适用对象，具备简单的模型思维；第三阶段，设在人教B版《普通高中教科书数学必修第三册》中，教师开展数学建模活动，促使学生用数学方法解决实际问题.

（2）思维能力.在第三阶段学习中，学生能够在抽象思维的基础上，利用简单的数学模型对知识点进行分类、归纳与总结，强化数学知识整合应用，形成数学建模思想，强化数学抽象思维能力.

（3）情感态度.高中阶段是学生升华探索精神的关键时期，在经历数学建模活动后，学生能够具备良好的合作学习精神、自主钻研精神，能够更加严谨、深入地开展学习活动，为形成良好的数学学科核心素养奠定坚实基础.

（4）学习障碍.第一阶段和第二阶段的建模活动相对简单、直观，第三阶段的建模活动具有抽象、复杂的特点，使得学生在面对这一阶段的建模活动时，容易产生畏难情绪，无法运用数学建模思想解决实际问题.同时，高中生解题过程中，容易将数学建模思想的运用错误理解为解答数学应用题，导致课程学习效率与质量降低.

1.2教学目标分析

教师对学生进行细致观察，了解高中生的数学学情，结合学生已有知识基础和身心规律，科学开展教学创新工作，深入渗透数学建模教学内容.教师应紧密关联新课标，设计出具有特色的建模教学活动，制定出详细的教学计划.

（1）情境与问题.在“周期现象的描述”的教学中，教师要引导学生自主学习，在具体情境、教学资料中提出问题，在数学模型建立与检测中解决实际问题，促使学生数学思维经历从现实到情境再到现实的过渡，切实提高学生自主学习能力.

（2）知识与技能.在探究“周期现象的描述”这一知识点时，教师帮助学生掌握“周期变化”的规律、特点，将理论与实际紧密融合，科学探索三角函数知识，为学生综合性发展开辟全新路径.

（3）思维与表达.教师利用“周期现象的描述”建模实践活动，引导学生探索y=Asin（ωx+φ）的函数公式，并利用函数表达的方法说明海水在一天内深度的变化过程，学生了解数学模型教学的主要方向和具体目标.

（4）交流与反思.通过完整的数学模型学习，学生能够形成独立意识和系统思维，进而主动与同学、教师等交流学习心得体会，分享自己的收获.学生自主体悟数学知识与生活实际的紧密联系，逐步建构自主、独立的数学建模思想，为形成良好的数学建模习惯做好铺垫.

1.3重点和难点

重点：教师引导学生感受数学建模从现实到情境再到现实的过程；促使学生掌握开题报告、论文书写等方式方法，提高其规划性学习能力.

难点：Excel 和 GeoGebra 的简单运用.

2教学过程设计

本课时的数学建模实践活动主要用“小组合作教学法”帮助学生完成建模准备，提高其对“建模教学”的预习与探索能力.在这一过程中，教师着重培养学生数据搜集和数据处理能力，提高其综合能力.基于此，“周期现象的描述”教学设计应略去选题过程，以开题为起点，直接进行实践教学研究.“周期现象的描述”课堂教学设计中，教师对各个教学环节的时间分配进行合理安排，具体安排见表1.

2.1问题情境

海水在24小时内会发生涨落现象.海上航道的开放与关闭都有规定的时间.海水上涨时，船只驶进航道；落潮时，船只驶回大海.在这一生活情境中，学生可以用函数对海水涨落情况进行描述，并探究港口水深与时间的变化.

2.2提出问题

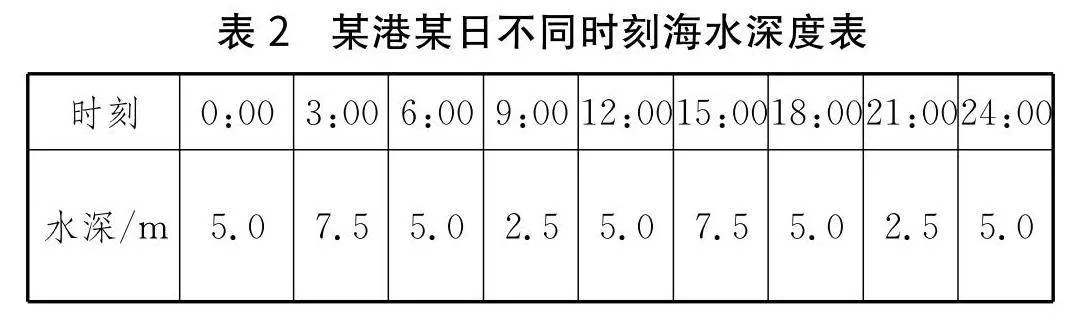
某港某日不同时刻的海水深度如下（见表2）.

师：结合所搜集的数据信息，用合适的函数描述24小时内这一港口的水深与时间的关系.根据二者的关系，探究各个整点时间的水深近似值.

生：在数据搜集过程中，能够获得准确、真实的数据，将这些数据进行处理后，可以制作成“散点图”. 在观察散点图后，判断船只进、离港时间可由哪一种函数描述.

【设计意图】新课标着重锻炼学生质疑能力，促使学生在具体问题中提高函数认知能力，并以函数知识为依据解决数学问题.这一学习环节能够培养学生数据搜集能力和数据分析能力，促使学生在分析数据过程中了解数学建模的方法和技巧，由此培养良好的建模思维.同时，在数据处理过程中，教师帮助学生强化信息化学习技能，掌握计算机的使用方法.

学习过程：将该港口不同时刻、海水深度的数据制作成数据关系表.同时，学生将具体数据在平面直角坐标系绘制出来（如图1）.

2.3建立模型

教师组织学生以小组合作的形式围绕“如何建立模型问题”进行讨论.

学生通过小组合作的方式讨论数据内涵，增强自身函数学习能力.

【设计意图】通过本学习环节的探索，教师培养学生自主学习、创新学习能力，学生利用散点图抽象出数学模型.

活动过程：教师利用散点图培养学生抽象思维意识.学生根据散点分布情况确定函数模型为正弦型函数，判断y=Asin（ωx+φ）+h 是否能够描述水深与时间关系.

2.4求解模型

师：各个小组选择正弦型函数，探索模型中的各个参数.

【设计意图】求解模型过程，学生对模型的参数进行分析，由此发现数学问题的解决方法，形成数学函数思想，提高函数知识解答能力.

实践过程：由数据、图象（如图2）可知，A=2.5，h=5，ω=π6.

将参数代入模型，得到函数y=2.5sinπx6+5 ，这一函数能够精准地描述某港水深与时间的数量关系.

2.5检验结果

师：同学们思考一下，接下来我们应该如何验证模型.

生：利用各个学习小组的研究成果，交流数学模型建构的规律和方法，由此掌握数学模型思维，强化学生学习能力.

【设计意图】在求解过程中，学生利用两组数据进行解题；通过检测建模模型，强化学生自主学习能力，提高自我检测技能，深化数学建模教学效果.

实践过程：学生将数据代入模型之中，通过推理计算检查是否有误；将散点与模型融合起来，绘制图象（如图3）.

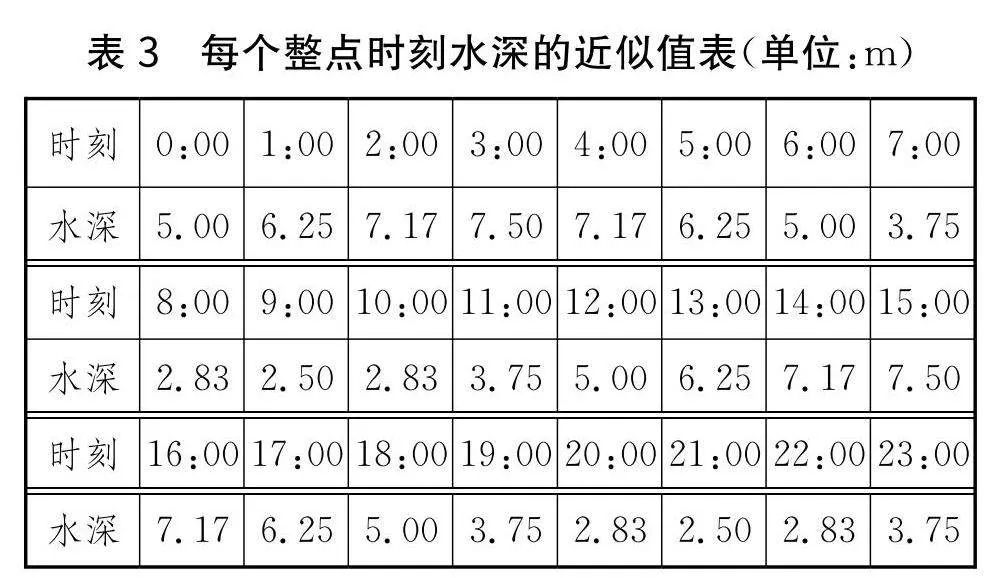
根据模型推导出整点水深（单位：m）近似值，具体数据如下（见表3）.

2.6实际应用

师：船底与水面距离4m，船底与水底最小距离为1.5m，这艘船要想驶进港口，需要在哪一时间，且可停留时间是多少.

生：利用小组合作学习法，在GeoGebra软件中绘制图象，分享学习心得体会.

实践过程：船底与水面距离为4m+1.5m=5.5m，即y=2.5sinπx6+5>5.5.用 GeoGebra 软件绘制函数y=2.5sinπx6+5的图象，并画出直线y=5.5，得到四个交点 A，B，C，D（如图4）.

3结语

本文以新课标为依据，对数学建模教学实践活动进行优化设计，结合高中数学建模思想培育目标，制定出符合高中生身心发展规律的数学模型教学方案，致力于培养学生良好的数学精神，强化学生数学综合能力.教师从“周期现象的描述”课程切入，帮助学生将生活实际问题抽象为数学模型，实现从现实到情境再到现实的学习目标，促进学生数学综合能力的发展.

参考文献

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.