素养导向视域下初中数学单元复习教学研究

摘要：现阶段初中数学期末复习存在教学方式固化，学生学习兴趣难以激发，教学活动单一等问题.因此在复习过程中学生很难提升自身分析问题、解决问题以及知识迁移的能力.本文以“等腰三角形”单元复习为例，详细展示了实际教学中单元复习设计的具体策略、取得的成效以及发展方向等.

关键词：单元整体复习；教学策略；等腰三角形

1当前单元复习教学存在的问题

笔者发现当前期末复习存在复习内容过于笼统，缺乏针对性和深度，复习方法单一，复习时间安排不合理等诸多问题.尽管学生在考前做了大量的试题，教师批改、讲评、再批、纠错等都落实到位，然而结果却不尽如人意，原因主要集中在以下几个方面.［1］

1.1教学方式固化

传统的教学方式注重机械记忆和应试技巧，导致学生对数学学习的兴趣不高，缺乏主动学习的动力.当前的复习教学，虽然教师能将讲解与练习相结合，但教学的方式单一，学生没有太多兴趣，无法全身心投入学习，只有部分学生被动掌握了一些简单的基础知识与基本技能.

1.2教学活动单一

大多数教师在上复习课时，总是先讲解，然后让学生练习，或者是学生先练习，教师后归纳总结.单一的教学活动导致只有少部分学生达到教学要求的目标、评价、结构和方法四维目标，绝大多数学生仅仅为了获得高分，忽视了数学思维与数学思想的培养，缺乏解决生活问题、科学问题等实际问题的能力，这样的教学活动很难达到联系生活情境、举一反三、知识迁移的效果.

1.3教学内容碎片化

大部分数学教师的单元复习教学环节清楚，能落实每节课的知识点，但是仍然存在学生掌握的知识点不扎实，没有真正理解所学知识的含义，不会整合与内化知识点，无法厘清所学知识部分与其他部分之间的关系，没有掌握解决综合问题的数学思维与数学方法等情况，从而使得教学无法达到预期目标.

2基于素养导向的数学单元复习教学的必要性和意义

2.1单元整体复习的内容是学生需要掌握的核心知识

通过单元整体复习，学生可以更加深入地理解和掌握数学基础知识，形成扎实的数学功底.同时，单元整体复习能够帮助学生将所学知识进行整合和串联，形成完整的知识体系，从而提升他们的数学思维和解决问题的能力.学生不仅能够理解知识的表面，还能够深入到知识的内核，掌握知识的本质和内在联系.这种深度理解的学习方式，有助于培养学生的思维能力和创新能力，使他们能够更好地适应未来社会.

2.2单元整体复习的教学设计相互关联，共同构成一个完整的教学框架

在目标上，单元整体复习教学强调培养学生的核心素养和综合能力；在评价上，单元整体复习教学注重过程性评价和表现性评价，帮助教师全面了解学生的学习情况；在结构上，单元整体复习教学通过构建知识网络，帮助学生理解知识的内在联系；在方法上，单元整体复习教学倡导学生主动参与、合作学习和探究学习，以激发学生的学习兴趣和积极性.

2.3单元整体复习设计有助于培养学生的自主学习能力和良好学习习惯

单元整体复习通过组题的形式、知识点的螺旋上升、数学方法的渗透、数学思想的深入逐步展示知识点的生成过程及知识点之间的联系.在复习过程中，学生需要主动参与、积极思考、及时总结，这不仅能够提升他们的学习效果，还能够培养他们的自主学习能力和学习习惯.这些能力和习惯对于学生未来的学习和生活都具有重要意义.

2.4单元整体复习设计能够促进教师的专业发展

在单元整体复习教学过程中，教师需要不断研究教学方法，更新教学内容，完善教学评价体系，提升自身的教学水平和专业素养.同时，教师通过与学生的互动和交流，可以更好地了解学生的学习需求和困惑，进而调整教学策略，提高教学效果.单元整体复习设计还能够激发教师的教学灵感，使教师从中学习到更多教学方法和策略.这些方法和策略对于教师的教学工作具有重大的指导意义.

3素养导向视域下的等腰三角形单元复习教学策略

3.1从结构上关注构建知识网络，帮助学生理解知识的内在联系

单元整体复习教学不仅仅是对知识点的简单回顾，更是帮助学生从整体上把握知识的结构和内在联系.通过构建知识网络，学生可以更好地理解各个知识点之间的逻辑关系，从而形成完整的知识体系.教师在课堂上以组题的形式进行归纳提升，通过解答一系列的问题，加深学生对知识点的理解和记忆，提升他们的思维能力和解题技巧.

组题1（问题串模式引导学生梳理归纳，实现拓展提升）.

（1）若等腰三角形的一条边长为3，另一条边长为4，则这个等腰三角形的周长为.

（2）等腰三角形一内角为70°，它的另外两个内角度数为.

（3）等腰三角形一个外角为110°，它的顶角为.

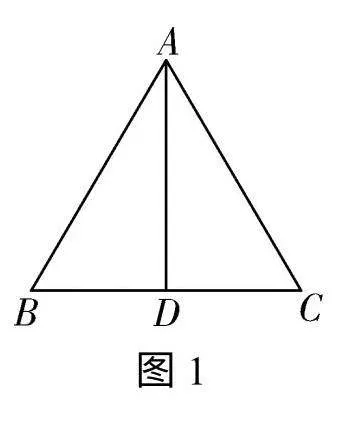
（4）如图1所示，已知等腰△ABC中，AB=AC，BC=6，AD=5，AD是BC边上的中线，则腰长AB=.

（5）已知BD是等腰△ABC一腰上的高，且BD与另一腰的夹角为50°，求△ABC顶角的度数.

（6）等腰三角形一腰上的中线把它的周长分为18厘米和21厘米两部分，求三角形的三边长.

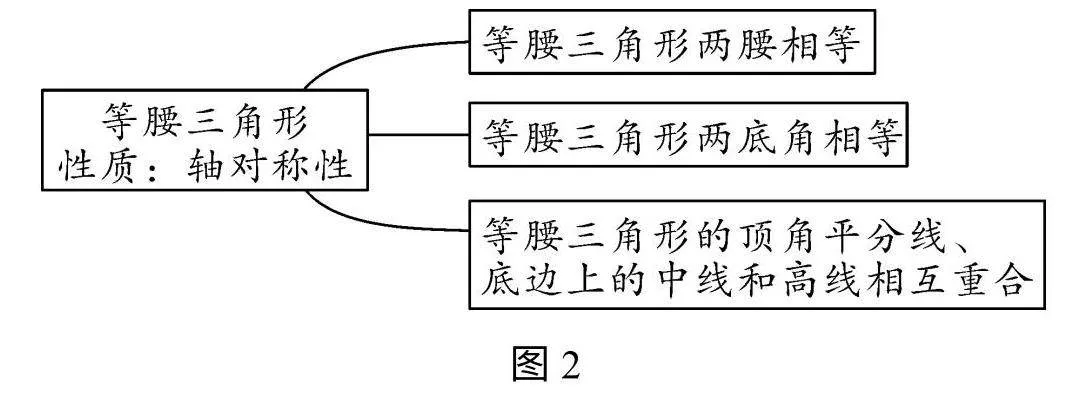
教师引导学生归纳出等腰三角形性质（如图2）.

教师再抛出问题：这几个性质中哪一条是核心内容.

教师让学生自己动手折叠等腰三角形纸片来感受等腰三角形的性质.这样的复习由浅入深，题目与知识点有对应与连接.学生感受并体会几何图形的特征，这对学生学习来说具有指导性与示范性，这种复习能够起到知识迁移的效果.［2］

教师继续追问：同学们做这几题的时候应该注意什么.

在教师的再次引导下，学生借助问题串的方法归纳出涉及的数学思想.学习效率在此过程中得到拓展与提升，从知识的表面升华到内涵，后续再做这类题目就会有完整的思维顺序.

组题2（学生先自主书写几何逻辑推理过程，教师后引导归纳总结）.

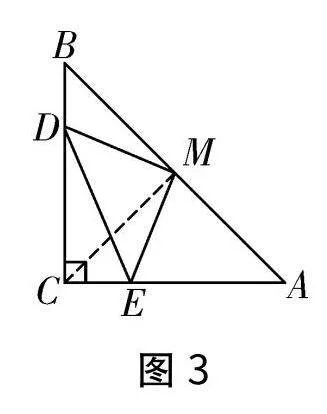
（1）如图3所示，∠C=90°，BC=AC，点D、E分别在BC和AC上，且BD=CE，M是AB的中点.证明：△MDE是等腰三角形.

（2）图4是一副三角板拼成的四边形ABCD，E为AD的中点.证明：△EBC是等腰三角形.

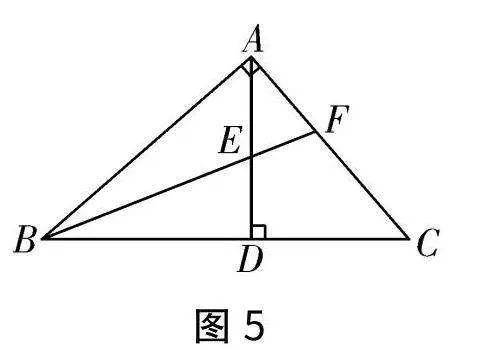
（3）如图5所示，Rt△ABC中，∠BAC=90°，AD⊥BC，D为垂足，∠ABC的平分线交AD、AC于点E、F.证明：△AEF是等腰三角形.

教师通过组题2的练习，加深学生对等腰三角形判定的理解，引导学生归纳整理判定的方法.

小贴士提醒：这类题旨在关注学生的逻辑推理过程，不能随意跳步骤或者是随意组合步骤，否则会出现逻辑性混乱与错误，而且这个阶段也需要严格规范书写步骤，为书写证明过程打好扎实的基础.

3.2单元整体复习教学在目标上强调培养学生的核心素养和综合能力

组题3（联系旧知——角平分线的有关分类及计算，通过添加平行线，获得新知识，切身感受双平等腰三角形的产生过程）.

（1）如图6所示，BE、CF是△ABC的角平分线，∠A=40°，求∠BOC的度数.

（2）如图7所示，BF、CE是△ABC的外角平分线，∠A=40°，求∠BOC的度数.

（3）如图8所示，BE、CF分别是△ABC的内角与外角平分线，∠A=40°，求∠BOC的度数.

在解题时，学生会很快回忆起∠BOC与∠A的关系，利用结论得到答案.教师对这三个图增加一个条件：过角平分线的交点O作第三边的平行线，设计以下例题，让学生说出新的结论.教师引导学生顺利得出结论：一条角平分线加上一条平行线就会出现等腰三角形.

例题如图9所示，在△ABC中，已知AB=13，AC=8，BO平分∠ABC，CO平分∠ACB.过点O作直线EF∥BC交AB于点E，交AC于点F.

（1）请问图中有多少个等腰三角形？说明理由.

（2）线段EF和线段EB、FC之间有没有关系？若有，是什么关系？

（3）△AEF的周长为多少？

3.3单元整体复习教学在方法上倡导学生主动参与、合作学习和探究学习

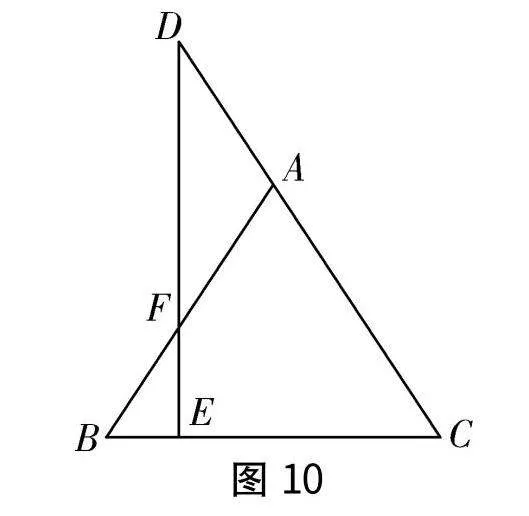
以浙江省杭州拱墅区2020-2021学年八年级（上）期末数学试卷第21题为例，本题第（1）问来源于浙教版《义务教育教科书数学八年级上册》第61页的第5题. 本题来源于教材又高于教材，解题方法较多，渗透一题多解，难度不大又具备一定的区分度.教师鼓励学生积极参与，认真探究，找到了10多种解法.第（2）问的辅助线添加是个重点. 中点加平行线构造八字形全等是常用辅助线方法，平行线在结点处添加.另外，第（1）问获得的等腰三角形常考三线合一定理也是一个提示功能. 教师在教学中有意识地引导学生学会数学上连续性的思维，这也是解决数学综合问题的关键.［3］

原题呈现如图10所示，在△ABC中，AB=AC，D为CA延长线上一点，且DE⊥BC交AB于点F.

（1）证明：△ADF是等腰三角形.

（2）若AF＝BF＝5，BE＝2，求线段DE的长.

解法：三线合一法.

（1）如图11所示，过点A作AG⊥BC交BC于点G.

∵AB=AC，

AG⊥BC，

∴∠3=∠4.

∵DE⊥BC，AG⊥BC，

∴DE∥AG.

∴∠D=∠4，∠2=∠3.

∴∠D=∠2.

∴AD=AF，

即△ADF是等腰三角形.

（2）∵AF=BF=5，DE⊥BC，

∴EF∥AG，

即EF是△BAG的中位线.

∴EG=BE=2.

∵AB=AC，AG⊥BC，

∴BC=4BE=8，EC=EG+GC=6.

∵DA=AF=5，AC=AB=10，

∴DC=AD+AC=15.

∴DE=152-62=321.

3.4单元整体复习教学在评价上注重过程性评价和表现性评价

单元整体教学试卷测评后，教师要做好试卷讲评课的具体落实工作，及时分析并有效讲评.课前学生自主订正其测试中非智力因素导致出错的问题.同时教师对班级试卷答题情况逐一分析，对于班级整体掌握

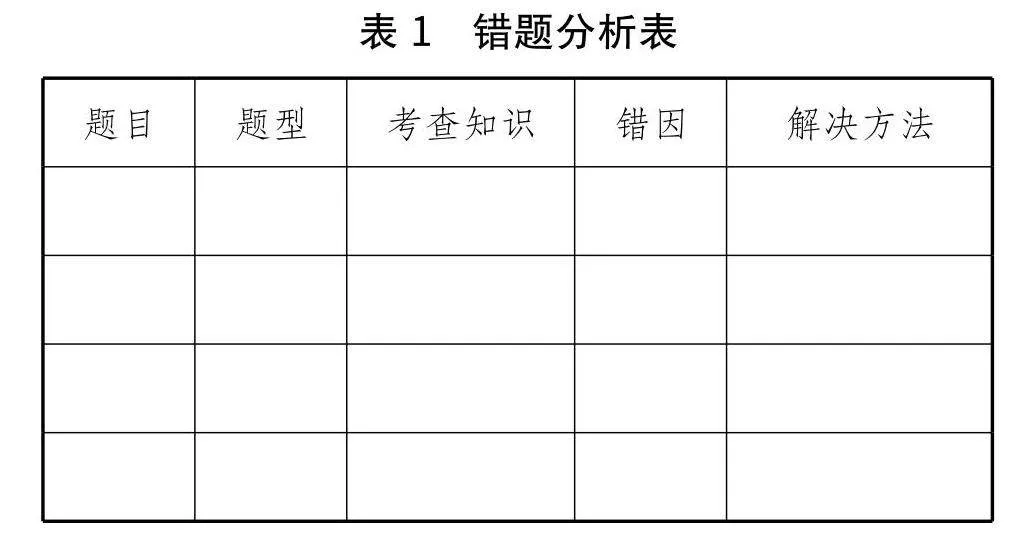
较弱的题目可以找同类题目或者是自编一些题目，要求学生再练习.课堂上，教师展示学生的错误，让学生找到错因并进行分析，并给出同类题目进行变式训练.课后教师让学生进行错题梳理，完成错题分析表（见表1）.通过展示典型错例，让学生相互指错、纠因、提出解决的办法，进一步独立完成配套的相应练习，并进行二轮纠错.同时教师将学生作业的纠错与梳理落实到位，将其作为正规的作业进行检查与批改.

3.5单元整体复习教学全面理解数学素养的内涵，注重培养学生的思维能力、创新能力和应用能力

笔者发现每年的八年级上学期期末考试中，会涉及一些求线段长度的题目，这类题往往涉及等腰三角形或者是直角三角形等特殊三角形，它是非常重要的知识点，也是试卷中的一个难点，经常是以填空题的形式或是解答题的某一问出现.学生每年的得分率都相对较低，如何提高此类题目得分率成为一大教学难点.

期末考试的原题都是教研员及其优秀团队经过精心思考打磨出来的，知识点分布均匀，知识面覆盖较广，难度系数控制得当，能考虑到各个层次的同学，紧跟省市中考命题方向，有一定的代表性、指导性.笔者的做法是利用好往年的区统测原题，把这些题目收集在一起做成专题，精讲精练，师生共同归纳出解题的完整思维与步骤，并要求学生规范地书写完整解答过程，反复练习.

^^原题呈现&&如图12所示，在△ABC中，∠ACB=90°，CD⊥AB于点D，AE平分∠BAC交CD于点F.若CF=3，BC=8，则DF的长为.

此题主要考核特殊三角形中的三线问题（中线、角平分线、高线），通常情况下

笔者引导学生学会四步法：分解图形—建构新图形—组合新图形—重建新模型.

方法点睛：

①分解过程.学生自主审题，将每个条件独立加工，获得这些条件可以得到的基本信息.

②组合过程.学生将两个或者三个条件组合加工，寻求知识点之间的联系.

③重点突出，攻破难点.量化图中某些线段，学生运用勾股模型、方程思想、几何问题代数化等方法解决问题.

④总结综合问题解法.完成解题后，教师引导学生总结做题方法，从特殊到一般，找到一般性结论和方法.

4基于素养导向的数学单元复习教学取得的效果

4.1学会举一反三

经过单元复习教学，学生学会举一反三，理解知识点之间的联系与区别，能够灵活地进行知识迁移，把一些复杂的综合问题进行拓展与深化，发展解决综合问题的能力.

4.2实现个性化教学和多元化的评价方式

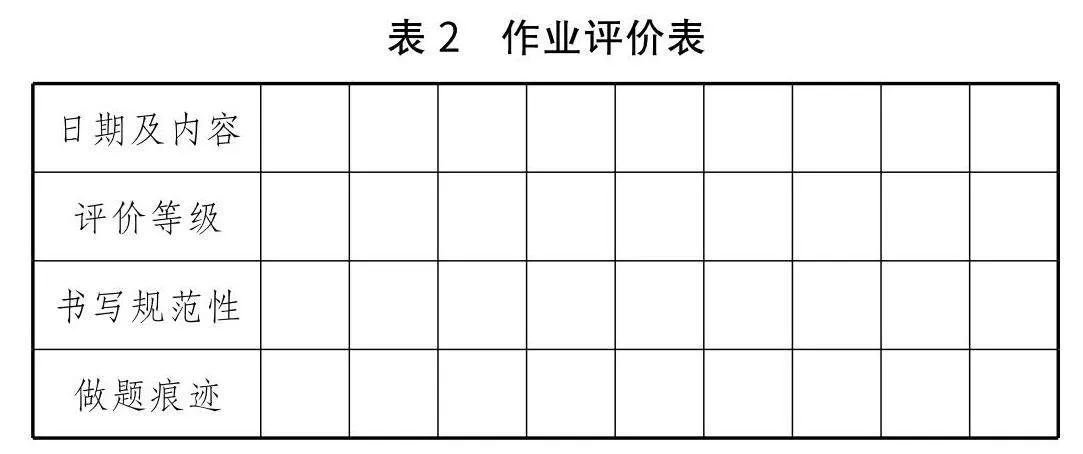
在平时的教学过程中，笔者把学生的家庭作业批改分为“优”“良”“差”三个等级，一个星期综合评价一次. 跟踪一个阶段之后，发现学生特别在意教师的作业评价，私下里会相互比较谁得的“优”多，对“优”的评价学生非常积极，经常为获得“优”与教师讨价还价，这种积极的反应给教师一种启发，努力做好作业多元化评价机制，从而提高作业质量.设计如下作业评价表（见表2）.

日期及内容栏中，学生写清楚作业的具体内容及日期；评价等级栏中，学生填写作业批改后的等级；书写规范性栏中，教师根据学生的书写情况、规范程度给出“优”“良”或“差”的评价；做题痕迹栏中，教师对做题留有标准痕迹的学生给予小贴纸形式的肯定评价.

实施该表后有以下好处：第一，有利于教师观察学生一个单元整体的作业进步或退步情况，及时关注退步的学生；第二，有助于激发学生的学习积极性，使学生在兴趣中自主优化自己的作业，从而提高作业质量；第三，教师对书写过程给予适当的评价有助于培养学生良好的作业规范性，班级作业规范度整体会上一个台阶H4rm8KuNBAZAB07a9yaTGw==.

通过个性化教学和多元化的评价方式，能够激发学生的学习兴趣和积极性，增强学生的自信心和学习动力，这将有助于形成积极的学习氛围，提高学生的学习效果.

4.3深化对数学核心概念的理解

通过单元复习教学和整合核心概念，学生能够建立起完整的知识体系，更好地把握数学学科的本质，这样的教学策略不仅有助于提高学生的数学成绩，更能培养学生的数学思维和解决问题的能力.

4.4提升数学素养和应用能力

通过专题式学习、问题解决等综合性强的复习活动，学生能够在实际应用中运用和巩固核心概念，从而提高数学素养和实践能力，这将对学生未来的学习和工作产生积极的影响.

5教学实施过程中发现的新问题及后期的发展方向

5.1教师对于素养导向的理解可能存在偏差

有些教师可能过于注重知识的传授，忽视了对学生数学素养的培养，或者对于数学素养的理解不够全面，导致教学效果不佳.

5.2教学方法单一，缺乏多样性

有些教师在实施单元教学时，可能只是简单地将知识点进行串联，教学方式缺乏创新和多样性，导致学生的学习兴趣不高，学习效果不佳.

5.3加强教师对素养导向的理解和培训

教师应该全面理解数学素养的内涵，注重培养学生的思维能力、创新能力和应用能力，而不仅仅是知识的传授.

5.4探索多样化的教学方法和手段，同时加强数学与实际生活的联系

教师应该根据学生的特点和需求，探索多样化的教学方法和手段，如案例教学、项目式学习、跨学科主题学习等，以提高学生的学习效果和学习兴趣.此外，教师应该注重数学与实际生活的联系，引导学生运用数学知识解决实际问题，提高学生的应用能力和创新思维.

参考文献

［1］施容容.核心素养导向的初中数学复习课设计探讨——以整式的加减为例［J］.中学数学研究（华南师范大学版），2020（10）：4-6.

［2］史承灼，季莹洁.基于单元教学 培养核心素养——以沪科版“等腰三角形”专题复习为例［J］.中学数学教学，2022（4）：14-17.

［3］施俊进.单元再建构：在知识结构中教与学——以“等腰三角形”单元教学实践为例［J］.中小学数学（初中版），2018（11）：1-4.