高考物理疑难问题专题突破(3)


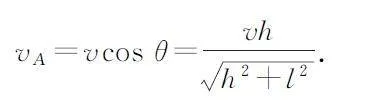


高中阶段,功、功率、动能定理、机械能守恒定律及能量守恒定律等知识是高考考查的重点,常结合其他动力学的重点知识进行综合考查.此类问题通常对学生的运动分析、受力分析及能量转化分析的能力要求较高,在复习过程中要做到夯实基础、强化能力、提升素养.本文对功与能专题中学生难以入手且易出错的几点疑难问题进行举例分析,希望能够帮助学生提高问题解决的能力,提升物理素养.
1 人做功问题
功是能量转化的量度,功的计算式W =FLcosα中的位移L 是力的作用点的位移.但很多问题中,运动的物体不能看作质点,比如人在原地起跳、爬楼梯、乘扶梯等,涉及人体做功问题时,如果对功的理解不深刻,对功的求解往往会出现错误.
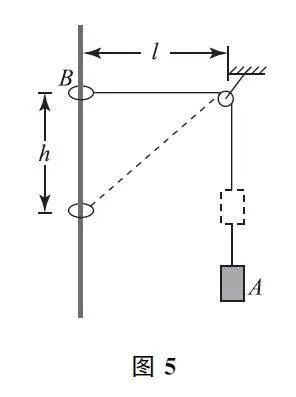
例1 如图1所示,在甲、乙两种情况下,人用同样大小的恒力拉轻质绳子,使人和船均向右运动,经过相同的时间t,甲中的船A 没有到岸,乙中的船A没有与船B 碰撞,则在此过程中( ).
A.甲中船A (包括人)的速度比乙中的船A (包括人)的速度大
B.甲中人对绳子的拉力的冲量比乙中人对绳子拉力的冲量小
C.甲中人对绳子的拉力的冲量和乙中人对绳子拉力的冲量一样大
D.两种情况下,人做的功一样多
解析 根据题意,两幅图中,拉力等大,作用时间相同,故拉力对绳子的冲量都为I=Ft,所以冲量一样大.由动量定理可知,合外力的冲量等于动量的变化,可知船末速度一样大.两种情况用同样大小的力拉绳,船A 向右移动的位移相同,船A 动能增加相同,但乙图中船B 也要向左移动,船B 动能也增加,故乙图中拉力做功多,选项C正确.
例2 自动扶梯以恒定的速度v 运转,运送人员上楼,一个人第一次站到扶梯上后相对扶梯静止不动,扶梯载他上楼过程中对他做功为W1,做功功率为P1;第二次该人在运动的扶梯上以相对扶梯的速度v同时匀速向上走,这次扶梯对人做功为W2,做功功率为P2.下列说法正确的是( ).
A.W1>W2,P1>P2
B.W1>W2,P1=P2
C.W1=W2,P2>P1
D.W1=W2,P1=P2
解析 两次所用时间不同,第二次用的时间少,力作用的距离短,两种情况人都处于平衡状态,电梯所给作用力相等,根据W =Fs,可知第一次做功多,即W1>W2.电梯匀速上行,速度不变,电梯对人的作用力都等于人的重力,根据公式P =Fv,可知两次电梯做功功率相等,即P1=P2.
小结 以上例题都涉及人做功,利用做功公式W =Fs 求解需要深刻理解s 的物理意义,s 指力直接作用在物体上时物体对地的位移.理解这点则以上类似问题可迎刃而解.比如,人原地起跳时,地面对人的作用力是人起跳的动力,由于力直接作用在人的脚上,而脚离地前没有位移,所以这个力对人并不做功.
拓展 如图2所示为无穷大水面,水面上有多块质量为M 、长度为2l 的首尾相连的漂浮的木板.一质量为m 的小孩(可视为质点)在某木板的中央,与该木板一起处于静止状态,小孩接下来开始在木板上表演“水上漂”.如果小孩能一次跳离木板(沿板长方向),求小孩第一次跳离木板时做功的最小值.不考虑水与木板接触面的阻力,设木板质量足够大且始终处于水面上.
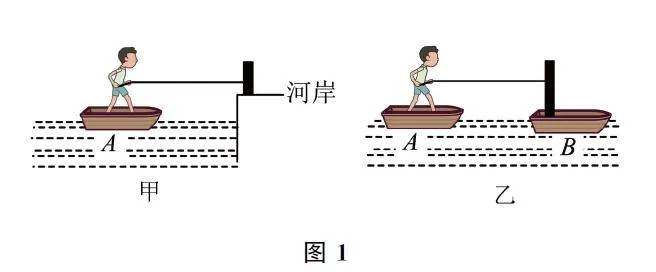
例4 如图4所示,水平桌面上的轻质弹簧一端固定,另一端与小物块相连,弹簧处于自然长度时物块位于O 点(图中未标出).物块质量m =1kg,弹簧劲度系数k=100N·m-1,物块与桌面间的动摩擦因数μ=0.1.现用水平向右的力将物块从O 点拉至A点,弹簧伸长量Δx=11cm,撤去拉力后物块由静止向左运动经O 点最远到达B 点.重力加速度g 取10m·s-2.下列说法正确的是( ).
A.物块在B 点所受弹簧弹力与在A 点大小相等
B.物块运动的总路程为60.5cm
C.物块最终停在O 点左侧1cm 内某处
D.物块最终停在O 点左侧1cm 处
解析 如果没有摩擦力,物块以O 点为平衡位置做简谐运动,则O 点应该在AB 中间,物块在B 点所受弹簧弹力与在A 点所受弹簧弹力大小相等,由于有摩擦力,物体从A 到B 过程中有机械能损失,故无法到达没有摩擦力情况下的“B”点,也即O 点靠近B 点,故物块在B 点所受弹簧弹力小于在A 点的弹力.物块最终停止的位置应满足kx ≤μmg,解得x≤0.01m=1cm,即物块若在O 点左右两侧1cm的范围内的速度为0,停止运动.
物体从A 到B 过程由能量守恒定律得
1/2k·Δx2=μmg(x1+Δx)+1/2k·x21,解得x1=0.09m=9cm.
物体从B 点往右运动到O 点右侧x2 过程由能量守恒定律可得1/2k·x21=μmg(x1+x2)+1/2k·x22,解得x2=0.07m=7cm.
以此类推,物体再次往左运动到O 点左侧x3=5cm处停止,再往右运动到O 点右侧x4=3cm 处停止,接着再往左运动到O 点左侧x5=1cm 处停止.物块运动的总路程为。
x总=Δx+2x1+2x2+2x3+2x4+x5=60cm,选项D正确.
小结 解决无限往返类的问题,找到规律至关重要.如例3应用动能定理求解路程,找到规律,最后进行数列求和.例4要应用能量守恒定律,通过计算前两次往复运动的位移规律,确定总路程和停下的位置.这些问题多涉及滑动摩擦力或其他阻力做功,其做功的特点是与路程有关,运用牛顿运动定律及运动学公式将非常烦琐,甚至无法解出,而动能定理只与物体的初、末状态有关,所以应用动能定理分析这类问题可使解题过程简化.
3 系统机械能守恒问题
对于功和能问题,学生基本能解决单个物体的机械能守恒问题,但对于多物体的系统机械能守恒问题以及非质点类的机械能守恒问题往往会比较难入手.
3.1 多物体的机械能守恒
在多个物体组成的系统内,若只有动能和势能的转化,则系统机械能守恒,解决此类问题关键是从三个角度建立关系式.1)能量关系式:系统的机械能守恒,通常选用转化式(ΔEk=-ΔEp)或转移式(ΔEA =-ΔEB );对系统内的单个物体,一般机械能不守恒,可以应用动能定理.2)位移关系式:根据几何关系,建立两个连接物的位移关系式.3)速度关系式:对于同轴转动的两物体,根据v=ωr 建立速度关系式;对于绳(杆)牵连的两个物体,根据沿绳(杆)方向的分速度相等,建立速度关系式.
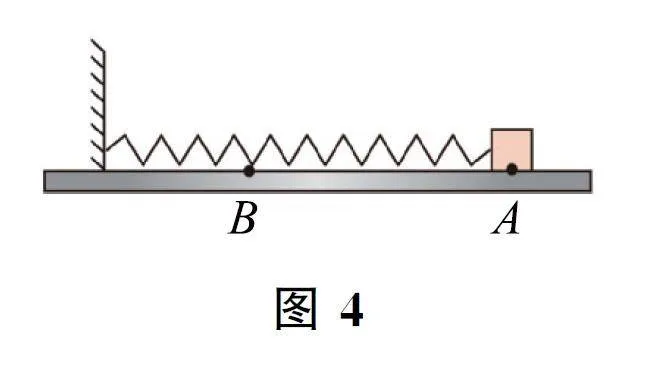
例5 如图5所示,物体A 的质量为M ,圆环B的质量为m ,通过绳子连接在一起,圆环套在光滑的竖直杆上,开始时连接圆环的绳子处于水平,长度l=4m,现从静止释放圆环.不计定滑轮和空气的阻力,g取10 m·s-2,若圆环下降h =3 m 时的速度v =5m·s-1,求A 和B 的质量关系.
解析 圆环下降3m 后的速度可以按如图6所示分解,故可得

