学习进阶模型的高三物理专题复习探索


学习进阶模型(learningprogressions,简称LPs)是指在一定时间内学习和探究某一主题时,依次进阶、逐级深化的思维方式.教师设计学习任务时,基于学生知识和常识,以内容领域为载体,让学生能够在解决问题的过程中思考逐渐深入、难度逐步加大、思维逐级进阶、素养自然提升,最终达到科学态度与责任的增强.
«普通高中物理课程标准(2017年版2020年修订)»提出:会用运动合成与分解的方法分析平抛运动,体会将复杂运动分解为简单运动的物理思想.在高三复习运动的合成与分解相关知识和方法时,利用学习进阶模型可以很好地落实该要求,并提升学生科学思维核心素养.
1 基本思路
“运动的合成与分解”作为一种重要的思想方法,将复杂运动分解为简单运动,本质上就是对描述运动的三个矢量“位移、速度、加速度”的合成与分解.
学习进阶的起点为定量研究蜡块的运动,“建立坐标系→蜡块运动的轨迹→蜡块运动的速度”.在“运动的合成与分解”的教学中,以获得知识的过程为方向,以思维发展的训练为重点,让学生经历把一个事物分解为几个部分进行研究,以及把几个部分结合成一个整体进行综合认识的思维过程,引导学生体会“等效”和“转化”的物理思想,提高学生的分析综合能力.
沿着“化繁为简”的思路,复杂运动可以分解为“直线运动与直线运动”到“直线运动与曲线运动”、“共面”到“不共面”、“匀速直线运动与匀变速直线运动”到“匀变速直线运动与匀变速直线运动”,再到“匀速直线运动与匀速圆周运动”,最后到“匀变速直线运动与匀速圆周运动”等类型,实现模型的学习进阶到思维的学习进阶.
2 教材实验分析
2.1 进阶起点:蜡块的运动
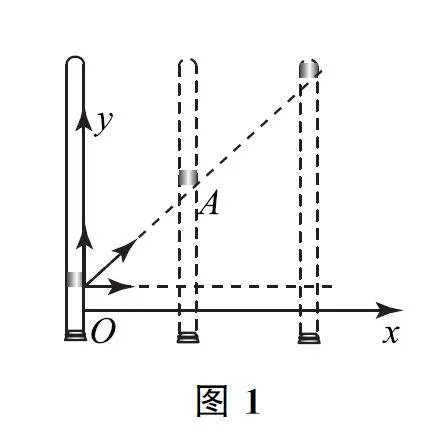
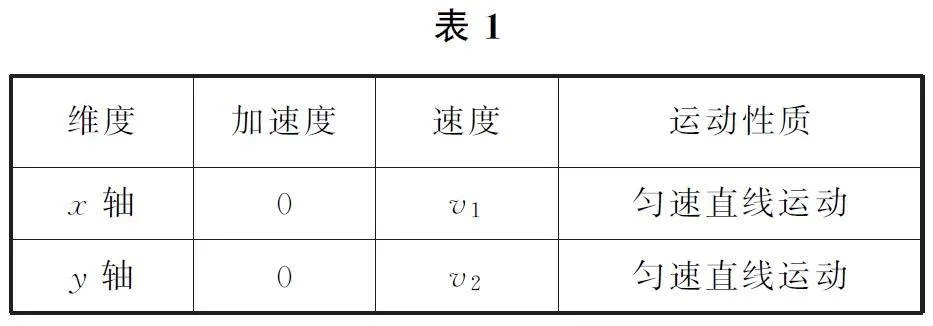
如图1 所示,从实验的角度,可8+U6TNlLzAozsSTnOiPDCA==以看到蜡块匀速上升的同时,玻璃管紧贴着黑板沿水平方向向右匀速移动.实际上,蜡块参与了水平方向的匀速运动和竖直方向的匀速运动.建立坐标系xOy,蜡块的运动分解如表1所示.
从理论的角度,蜡块沿x 轴和y 轴的加速度分别为a1=0和a2=0,其合加速度一定为a=0;蜡块沿x轴和y 轴的速度分别为v1 和v2,其合速度大小为v=根号下v21+v22;蜡块沿x 轴和y 轴的位移分别为x =v1t和y=v2t,其合位移大小为s=根号下 x2+y2 .
例1 若人在河中始终保持头朝正前方游向对岸,你认为他会在正对岸处到达,还是会偏向上游或下游? 为什么? 他如何才能到达正对岸.
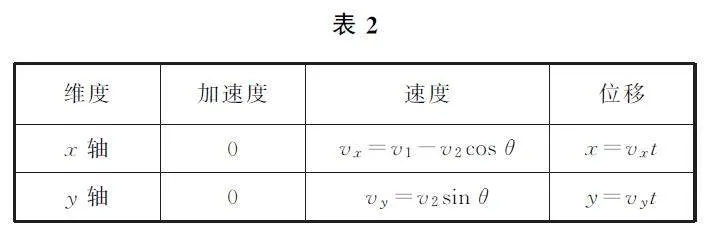
解析 设河宽为d,沿河岸的水流速度为v1,人在静水中的速度为v2,人保持头朝上游且与河岸成θ 角游向对岸.沿河岸和垂直河岸建立坐标系xOy,人的运动分解如表2所示.
当vx >0时,x>0,人到达正对岸的下游位置;当vx =0时,x=0,人到达正对岸的位置;当vx <0时,x<0,人到达正对岸的上游位置.
2.2 进阶1:匀变速直线运动
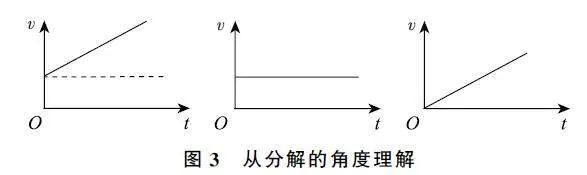
根据速度与时间的关系式v=v0+at 和位移与时间的关系式x=v0t+1/2at2 分析,匀变速直线运动可以理解为:速度为v0 的匀速直线运动和初速度为0、加速度为a 的匀变速直线运动的合运动.
从vGt 图像可以得到同样的结论,如图2、3所示.
2.3 进阶2:平抛物体的运动
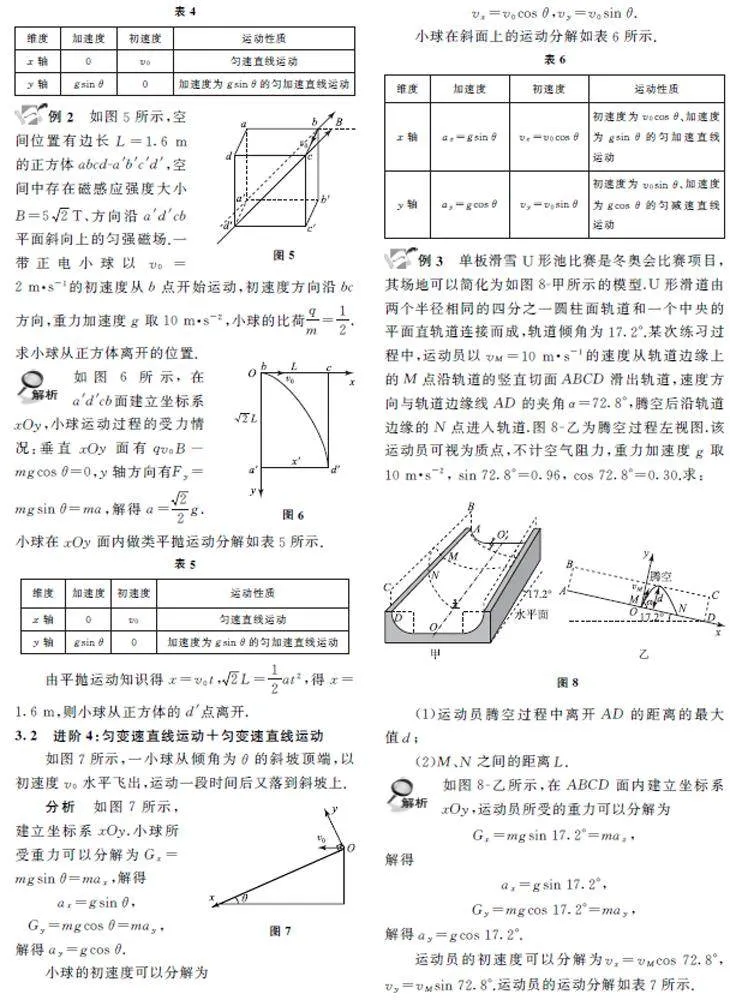
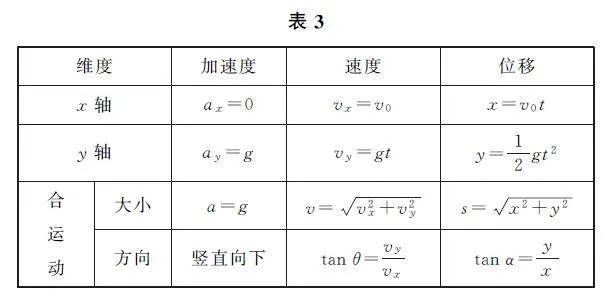
从实验和理论的角度分析,平抛运动分解如表3所示.
3 复习策略
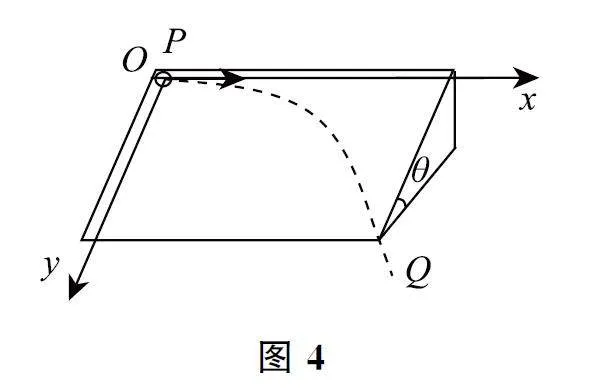
31 进阶3:类平抛运动
如图4所示,一倾角为θ 的光滑斜面.一小球从斜面左上方P 点以初速度v0 水平射出,最终从斜面右下方Q 点离开斜面.
小球在斜面上运动的受力情况:沿斜面向下方向有mgsinθ=ma,得a=gsinθ,垂直斜面方向有FN=mgcosθ.如图4所示,在斜面建立坐标系xOy,小球在斜面上的运动分解如表4所示.

