对以“做”促“学”的综合实践课的探索与思考

摘 要：基于学生解决实际问题能力薄弱的特点，开发“综合与实践”课程，指导学生将“学”与“做”结合起来，培养学生运用数学知识解决实际问题的能力. 选取折纸活动，聚焦折出正方形边上的三等分点问题，让学生经历发现问题、提出问题、分析问题、解决问题和反思方法的过程，培养学生的知识综合应用能力和数学核心素养.

关键词：综合与实践；数学活动；折三等分点；应用能力

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）08-0037-06

引用格式：宋菲，易良斌. 对以“做”促“学”的综合实践课的探索与思考［J］. 中国数学教育（初中版），2024（8）：37-41，57.

在教学中，我们发现学生解决实际问题的能力远低于解决数学问题的能力. 很大一部分原因是数学教学中解决的数学问题远多于实际问题，使得学生解决实际问题的经验比较少. 同时，解决实际问题需要学生能将实际问题转化为数学问题，调用已有的数学知识寻找解决问题的方法，这对学生的知识综合应用能力要求较高.

“综合与实践”课程的教学多以问题为引领，让学生在实践中综合运用所学的知识解决问题，从而有效提高学生解决实际问题的能力，培养学生的应用意识，让学生积累数学活动经验.

笔者曾设计“如何折出正方形边上的三等分点”一课，以期丰富数学课程，激发学生的学习兴趣，提高学生解决实际问题的能力，培养学生的数学关键能力，发展学生的数学核心素养.

一、教学实践

本节课是针对九年级学生开展的综合与实践拓展课.《义务教育数学课程标准（2022年版）》（以下简称《标准》）指出，综合与实践领域的教学活动，以解决实际问题为重点，以真实问题为载体，适当采取主题活动或者项目学习方式呈现. 其中，项目学习教学以用数学方法解决实际问题为主，其目标是引导学生发现解决现实问题的关键要素，用数学的思维分析要素之间的关系并发现规律，培养模型观念，经历发现、提出、分析、解决问题的过程，培养应用意识和创新意识.

因此，综合与实践领域的教学活动要选取贴近学生生活的，且能用数学思维解决的，能用数学语言表达的真实问题. 下面笔者将围绕以上要求，谈谈这节课的教学设计.

1. 生活视角，选取问题背景

数学既来源于生活，又应用于生活. 因此，教师需要发现生活中的数学问题，并且能根据学生的知识储备和认知规律，创设可以研究的问题情境. 折纸是学生在小时候就接触过的实践活动. 同时，现代折纸学已经将折纸应用于工业、医学、航天等方面. 例如，在航天领域，应用折纸原理制作的太阳能电池阵列，既可以紧密压缩存放在航天器内，进入太空后又可以精确展开，这样的设计缩小了太阳能电子板的体积. 所以创设与折纸有关的问题情境能激发学生的学习兴趣.

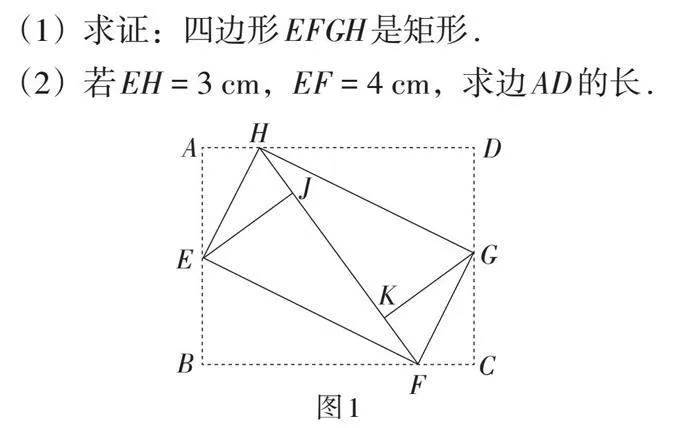
折纸的本质是折叠，即轴对称. 在初中各版本的数学教材中多处出现了以折纸为背景的几何问题，如浙教版《义务教育教科书·数学》八年级下册第117页的作业题：如图1，将矩形纸ABCD的四个角向内折起，恰好拼成一个无缝隙、无重叠的四边形EFGH．

（1）求证：四边形EFGH是矩形.

（2）若EH = 3 cm，EF = 4 cm，求边AD的长.

【教学说明】折纸活动起点低，容易让学生产生学习的兴趣，折叠方法多样，能让学生在课堂上动脑、动手、动口，积累数学活动经验.

2. 数学眼光，聚焦核心问题

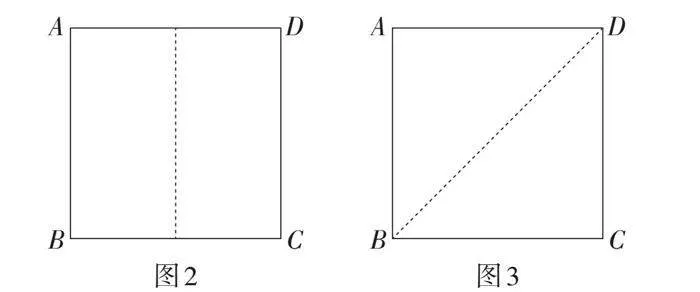
在折纸活动中，什么样的问题能引发学生思考，并且能促进学生能力的提升呢？一次折叠中，最核心的折法有两种. 一是将线段二等分（如图2），二是将直角二等分（如图3）. 实际上，通过一次折叠，可以二等分一条线段或二等分一个角. 另外，所给的图形是正方形纸片，强化了折叠的条件. 也就是说，只要纸片上存在一条线段或一个角即可通过折叠实现二等分.

从研究几何对象的角度来看，如果将折纸的结果归类为线段问题、角度问题、图形问题，那么就可以研究三等分、四等分、黄金分割、30°角、等边三角形等问题. 具体归类如下：三等分、四等分、八等分、黄金分割……；22.5°角，30°角，60°角……；矩形、等腰三角形、等边三角形……

在教学中，可以通过师生对话的形式引出上述问题并进行归类. 因为三等分问题是除了2n等分问题之外最简单的问题，是学生能利用已学习的数学知识解决的问题，所以本节课聚焦的核心问题是如何折出三等分点.

【教学说明】折出三等分点的方法有很多，研究这个问题能发散学生的思维，培养学生的创新能力. 同时，研究中所学到的思想和方法能帮助学生解决其他问题. 在教学中，从学生的已有知识入手，回顾旧知，通过教师逐步引导聚焦三等分问题，充分调动学生的主动性，在发现问题和提出问题的过程中，体现学生的主体地位.

3. 几何建模，探寻解题之道

问题：当所给的纸片是正方形时，如何折出正方形边上的三等分点呢？

师生活动：教师在课堂上给予学生充分思考的时间，并提供给学生交流的空间. 最后，在课堂上展示学生的交流成果.

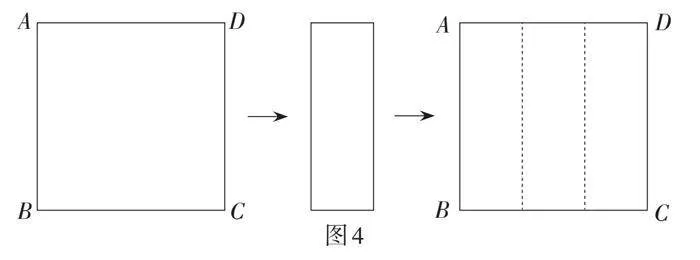
方法1：将正方形纸片卷起来形成三层，并不断地调整，得到边上的三等分点，最后将纸展平. 折纸步骤如图4所示.

【教学说明】方法1是大部分学生根据生活经验所得的，也是最为常见的折法. 在教学中，教师肯定学生的折法是直观的，并介绍这是几何发展的第一阶段——经验几何阶段. 部分学生会提出这种折法不够准确，于是为后续折法作铺垫.

除了方法1，很多学生想不到其他折法. 此时，教师引导学生将实际问题转化为数学问题，让学生思考三等分的数学意义及符号语言. 学生试着将问题转化为：在正方形ABCD中，折出点M使得[AMAD=13]. 然而涉及线段的比例问题常常可以联想平行线分线段成比例定理及相似三角形的性质，将三等分转化为二等分或者四等分，所以不难得到以下方法.

方法2：如图5，连接AC，BM交于点H，此时△AMH ∽ △CBH. 要使得[AMAD=13]，即[AMBC=13]，则只需满足[AHCH=13]. 所以只要折出对角线AC上的四等分点H就能解决问题.

[图5][B][A][D][C] [M][H]

方法3：如图6，MF∥DG，要使得[AMAD=13]，则只需满足[AFAG=13]. 如图7，连接AC，折出AC上的四等分点F，G，连接DG，过点F作DG的平行线，交AD于点M，此时M是边AD的三等分点.

方法4：如图8，连接AC，作MF∥DC，交AC于点F. 要使得[AMAD=13]，则需满足[AFAC=13]. 连接BF并延长交AD于点E，此时△AEF ∽ △CBF. 根据相似三角形的性质，不难得到E是边AD的中点. 所以折法如下. 折出AD的中点E，连接AC，BE交于点F，将线段AB沿着过点F的直线对折，使得MF∥AB，直线交AD于点M，此时M是边AD的三等分点.

【教学说明】方法2至方法4是利用相似三角形的性质或平行线分线段成比例定理，将三等分问题转化为已知的二等分问题来解决. 在问题解决的过程中，需要先将三等分问题转化为数学语言来表达，然后能联想到利用相似三角形的性质将线段之比进行转化. 在此过程中渗透了数学建模的思想和化归思想.

对于三等分问题，除了从比例的角度进行思考，还能从计算的角度着手解决. 此时，教师可以引导学生回顾常见的求线段长度的方法，将问题转化为以前所做过的题目，得到以下方法.

方法5：如图9，折出DC的中点E，连接BE，将△CBE沿BE折叠至△BC′E；然后将边AB翻折至与边BC′重合，此时折痕与AD的交点M是边AB的三等分点.

需要证明M，C′，E三点共线. 可以设正方形的边长为1. 如图9，因为E是DC的中点，所以DE = CE =[12]. 设AM = x，则C′M = x，DM = 1 - x. 根据勾股定理，在Rt△DME中，有ME2 = MD2 + DE2，即[x+122=1-x2+]

[122]. 解得[x=13].

方法6：如图10，折出DC的中点E，折叠使得点B与点E重合，此时AB的对应边A′E与边AD的交点M是边AD的三等分点.

设BF = EF = x，则FC = 1 - x. 在Rt△CEF中，根据勾股定理，得EF2 = FC2 + EC2，即[x2=1-x2+122]. 解得[x=58]. 再利用△CEF ∽ △DME，求得DM =[23]. 所以AM =[13].

【教学说明】在证明方法5和方法6时，需要用到正方形的性质、折叠的性质、勾股定理、相似三角形的性质，覆盖了几何的核心知识，提高了学生的综合解题能力. 同时，方法5和方法6相对于前三种折法更简单，是对三等分折法的一种优化. 因此，在这个过程中，不仅要潜移默化地引导学生解决问题，而且要用优化的方法解决问题.

4. 问题延伸，推广数学模型

方法5是芳贺第二定理，方法6是芳贺第一定理.此时，教师引导学生对芳贺定理进行推广，将点E是中点的条件推广为任意点. 也就是说，在边长为1的正方形ABCD中，当点E在边DC上运动时，思考：点M的位置会有什么样的变化？如何表示这两个变量之间的关系？

如图11，设CE = x，AM = y，则DE = 1 - x，DM = 1 - y. 根据折叠的性质，易得ME = x + y. 在Rt△DME中，有[DE2+DM2=ME2]，即[1-x2+1-y2=x+y2]. 化简，得[y=1-x1+x]. 也可以用三角函数求解. 设∠ABM = α，∠CBE = β. 由折叠，得∠MBE = α + β = 45°. 则[tanα+β=tan45°]. 所以[tanα+tanβ1-tanαtanβ=][tan45°，] 即[x+y1-xy=1]，得[y=1-x1+x].

如图12，设CE = x，BF = a，AM = y. 根据折叠的性质，得EF = a. 在Rt△CEF中，[CF2+CE2=EF2]，即[1-a2+x2=a2]. 解得[a=x2+12]. 再根据△DME ∽ △CEF，得到[DECF=DMCE]，即[1-x1-a=1-yx]. 化简，得[y=1-x1+x].

对芳贺定理进行模型推广，我们能得到线段AM关于线段CE的函数关系式为[y=1-x1+x]. 但是为什么图11和图12得到的结果是一致的呢？

我们可以在图12的基础上连接BM，BE，得到图13. 根据折叠，得∠FBE = ∠BEF，则∠MEB = ∠ABE. 又因为AB∥DC，所以∠ABE = ∠BEC. 过点B作BP⊥ME于点P，易证△CBE ≌ △PBE，△AMB ≌ △PMB. 得∠PBE = ∠CBE，∠ABM = ∠PBM. 则∠MBE = 45°. 所以图11和图12得到的结论相同，即芳贺第一定理与芳贺第二定理的本质相通. 在教学中，教师可以让学生对芳贺定理中的一种进行推广即可.

【教学价值】引导学生发现线段AM的长度变化是由点E的运动所导致的，可以用关于线段CE的函数关系式来刻画，从而将问题从特殊引到一般，从不变引向变化，拓展学生思维的深度. 这个过程是将几何问题代数化，渗透从特殊到一般的数学思想及数学建模思想. 学生从大致折出三等分点（方法1）到利用数学知识准确折出三等分点（方法2至方法6），再到寻找折出线段等分点问题的一般方法（芳贺第一定理和芳贺第二定理的模型推广），经历了经验几何、古典几何、解析几何的过程，感受了几何文化.

5. 数形结合，提升综合能力

函数[y=1-x1+x]，即x + y + xy = 1. 这是一个轮换对称式，具有对称性，有一定的研究价值. 因此，教师可以引导学有余力的学生借助图象对函数[y=1-x1+x]的性质进行探索.

按照一次函数、反比例函数、二次函数的研究方法，确定研究思路，即运用描点法画出函数的大致图象，进而研究函数的性质.

图14是函数[y=1-x1+x]的图象. 发现该函数图象也是双曲线. 因此，思考函数[y=1-x1+x]是由什么样的反比例函数通过怎样的平移得到的.

因为[y=1-x1+x=2x+1-1]，所以[y=1-x1+x]是由反比例函数[y=2x]先向左平移1个单位长度，再向下平移1个单位长度所得. 所以[y=1-x1+x]关于点[-1，-1]中心对称，关于直线y = x或直线y = -x - 2轴对称.

线段AM关于线段CE的函数具有轴对称性的本质是正方形的轴对称性. 因此，教师还可以引导学生观察特殊点，根据正方形的轴对称性猜测[y=1-x1+x]具有轴对称性. 具体做法如下.

问题1：当[y=13]时，x的值是多少？当[x=13]时，y的值是多少？

当[y=13]时，[x=12]，即E是DC的中点，折法如图15所示，即芳贺第一定理. 如图16，当[x=13]时，[y=12]，即M是AD中点，点E是DC的三等分点，这是芳贺第三定理.

问题2：从[x=12，y=13]与[x=13，y=12]中，你能发现什么？

可以发现函数[y=1-x1+x]具有对称性. 将图15和图16简化，并组合在一幅图中（如图17），发现线段AM关于线段CE的函数具有对称性的本质是正方形的轴对称性.

【教学价值】运用函数的研究路径对[y=1-x1+x]进行研究，从几何过渡到代数，提升学生的综合应用能力.同时，教师引导学生从特殊点猜想函数的对称性，渗透了从特殊到一般的数学思想. 从图形的角度说明函数的性质，揭示其本质，体现数形结合思想.

二、教学思考

“综合与实践”课程以活动为载体，让学生会用数学的眼光发现问题，会用数学的思维思考问题解决的思路，会用数学的语言表达问题解决的方法. 在这个过程中，数学的学习不是模仿记忆，而是有创造性地发现知识，有效地培养学生的关键能力，发展学生的数学核心素养.

1. 数学生活化，化被动为主动，凸显学生主体

“综合与实践”课程要贴近学生的实际生活，且能让学生感受到数学的价值，从而激发学生学习数学的兴趣. 本节课以学生熟悉的折纸活动为载体，引导学生聚焦如何折出正方形边上的三等分点. 学生通过动手操作、动脑思考，运用相似三角形的性质、勾股定理等数学知识探寻正方形边上三等分点的折法，甚至还可以将方法推广，折出任意等分点，从而感受数学学习为生活服务的理念. 在探究过程中，学生经历经验几何（方法1），古典几何（方法2至方法6）到解析几何的过程，渗透了几何文化，感受了数学的发展源于实际的需要，获得自身成长和发展的力量. 在此过程中，学生学习数学的方式由被动接受转化为主动探究，凸显了学生学习的主体地位.

2. 思维可视化，从具体到抽象，经历建模过程

通过折叠寻找正方形纸片边上三等分点的问题时，首先要将实际问题转化为数学问题，并表示成图形语言和符号语言，在此过程中，发展了学生的几何直观；其次，根据得到的结论[AMAD=13]，联想平行线分线段成比例定理、相似三角形的性质、勾股定理等数学知识，通过推理寻找解决问题的方法，培养学生的应用能力；最后，通过芳贺第一定理和芳贺第二定理找到线段AM关于线段CE的函数关系式，从而找到正方形边上任意等分点的折叠方法，培养学生对问题迁移应用的能力.

在教学中，教师引导学生从实际问题中抽象出数学问题，再利用数学的知识和方法解决问题，最后建立函数模型，寻求一般化方法. 每个步骤中，学生通过独立思考、动手实践、师生交流等不同的学习方式呈现了思维的发展过程，将思维可视化. 学生经历了由具体问题抽象到数学问题，由解决具体问题抽象到解决一般化问题的过程，实现了对数学核心素养的培养.

3. 评价过程化，由单一到多样，实现多元评价

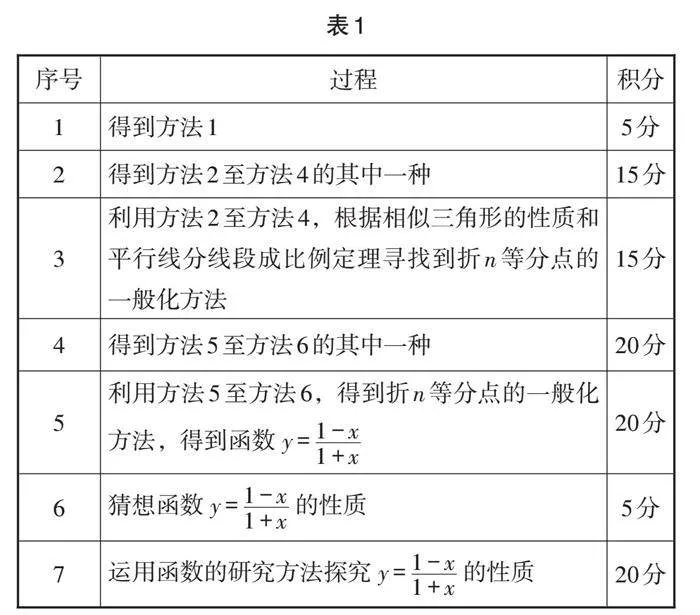
折出正方形边上的三等分点的方法有很多，本节课仅展示了其中一部分，每种方法的思维方式不同，可以根据方法优劣进行不同层次的评价. 因此，本节课可以采用积分制对学生进行评价，具体流程如表1所示.

将评价过程化之后，学生在学习过程中就可以根据自身的能力选择不同深度的学习，从而使得统一学习变成了个性化学习，满足不同学生的不同需求. 同时，引导学生用不同的方法解决问题，培养了学生的应用意识和创新意识.

三、结束语

开发贴近学生生活，利于实现数学学科育人目标的“综合与实践”课程需要教师用心关注生活中的数学问题，擅于挖掘教材中的数学问题. 当教师拥有一双发现数学的眼睛时，可以培养学生用数学的眼光观察现实世界.

参考文献：

［1］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］陆新生. 从芳贺第一定理看折纸数理学的教育价值［J］. 上海中学数学，2007（12）：1-4.

［3］陆新生. 正方形折纸一边三等分方法的探究［J］.上海中学数学，2014（12）：21-24.

［4］董林伟.“做数学”：中小学生适合教育的实践构建［J］. 教育研究与评论，2021（3）：16-21.