高中数学建模核心素养的落地

当前课程改革和课堂教学进入核心素养引领的时代。一方面，数学建模搭建了数学与客观世界的桥梁，是数学应用的重要形式，是应用数学解决实际问题的基本手段，也是推动数学发展的动力，已成为数学学科六大核心素养之一，对于整体提升数学学科核心素养和中国学生发展核心素养具有支撑作用。另一方面，由于缺乏适用的教学素材和详细的教学指导，教师普遍感觉在课堂中开展数学建模教学存在困难。课程是实现核心素养的核心，课堂教学是课程实施的主渠道，如何在数学课堂上由普通数学知识的教授过渡到学生数学建模核心素养的培养，需要我们持续探索。

一、基于教材创建高中数学建模课堂框架

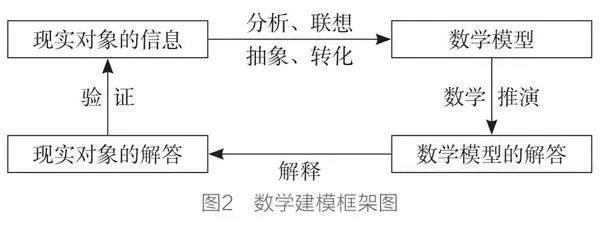
我们基于人教B版各个数学模块，梳理数学知识，在各个模块数学应用的基础上，设计相应的数学建模小案例，实现数学建模水平一到水平二能力培养的合理进阶。本文以函数部分为例，给出从函数应用到函数建模的课程实践（见图1）。

二、梳理函数知识结构

在现实世界里，事物之间存在着广泛的联系，当面对的实际问题中存在几个变量，并且它们之间具有依赖关系时，我们往往用函数对其进行刻画。函数的表达可以使用列表、图像，但高中阶段最常见的还是使用解析式（见表1）。

教师引导学生借助软件作常见的函数模型的图像、复习函数的增减性等，引导学生关注函数定义域，给建模过程中用描点法协助寻找合适函数解析式打下基础。

三、以函数应用题为载体，巩固函数模型

考试中的函数应用题被划分为阶段一的建模培养，是学生最直接、最容易接受的“初级建模”问题。

1. 了解数学模型中的参数、结论的实际含义

了解熟悉的数学模型的实际背景及数学描述，了解数学模型中的参数、结论的实际含义，对于学过的数学模型，体会其蕴含的数学思想，是数学建模核心素养水平一的要求。

在实际问题中，声音等级、地震等级、溶液酸碱度、星星亮度等级等经常用对数模型表示。对数是学生高中接触的最难理解的函数之一。本文借助下面的题目让学生充分理解对数型函数中自变量、函数的意义，感受对数函数关于自变量的增长量级。

案例1：人们通常以分贝（符号dB）为单位来表示声音强度的等级，其中0dB是人能听到的等级最低的声音。一般地，如果强度为x的声音对应的等级为f（x）dB，则有f（x）=10lg 。

①树叶沙沙响的声音强度是10—12，计算它的声音等级。

②计算出90dB的声音与60dB的声音强度之比。

教师借助案例1引导学生一遍有效读题。在案例1中，声音强度即x，声音等级是f（x），将题目中的强度和等级直接替换为x，f（x），实际问题转换为纯对数函数问题，学生通过对数函数模型求解，最后将结果还原到实际问题中的强度和等级，解决实际问题。

2. 选择合适数学模型解决数学问题

能够在数学的情境中，发现问题并转化为数学问题，选择合适的数学模型表达要解决的数学问题，确定参数、建立模型、求解模型是数学建模核心素养水平二的要求。

（1）通过分析实际问题的意义，建立模型

在实际问题中，有关人口增长、银行利率、细胞分裂等增长率问题常用指数函数模型表示。

（2）通过分析图像，分析函数模型

实际问题中的大部分函数无法直接写出函数关系式，可以通过描点等方法作出函数图像，所以，有些题目中直接给出函数图像，学生就图像分析问题，建立模型，得出结论。

（3）一题多解，模型选择

读懂题意，设变量，在题目中找等量关系，将变量代入等量关系列出解析式，按解析式函数性质、均值不等式等求解。在建立函数模型解决实际问题时，一定要注意自变量的取值范围，尤其要注意实际背景带来的取值范围，如二次函数根据函数图像的对称轴与函数定义域的位置关系讨论求解，最优解有时在对称轴处取得，有时在区间端点处取得。

高一学生学完基本初等函数之后，在求最优解的数学模型中，除了二次函数，均值不等式模型也是常用模型之一。均值不等式求最值注意事项如下。

已知xgt;0，ygt;0，（“一正”），则

①若x+y=s[和为定值（“二定”）]，则当x=y（“三相等”）时，积xy取得最大值；

②若xy=p[积为定值（“二定”）]，则当x=y（“三相等”）时，和x+y取得最小值。

学生可以简单记为：“一正、二定、三相等”。

（4）分段函数模型

很多实际问题中，变量间的关系不能用一个关系式给出，这时就需要构建分段函数模型，如出租车的票价与路程的函数就是分段函数。分段函数在每个区间上依据题目变量之间的关系可以是一次型、反比例型、二次型、指对幂型等。

案例2：设某商品的利润只由生产成本和销售收入决定。生产成本C（单位：万元）与生产量x（单位：千件）间的函数关系是C=3+x；销售收入S（单位：万元）与生产量x间的函数关系是

①把商品的利润表示为生产量x的函数；

②为使商品的利润最大化，应如何确定生产量？

解：①设商品的利润Y（单位：万元），依题意得

②当0 lt; x lt; 6时，

当且仅当时，即x=5时取等号，所以

当0 lt; x lt; 6时，Y有最大值6，

当x 6时，Y=11―x" 5.

综上，当x=5时，Y取得最大值6，因此，当生产量为5千件时，商品的利润取得最大值6万元。

分段函数题型的解题规律与方法主要有：在求分段函数的最值时，应先求每一段上的最值，然后比较得出最大值、最小值。每个区间上的最值，可以用基本不等式法、导数法、函数的单调性等方法求得。

四、数学应用基础上的数学建模

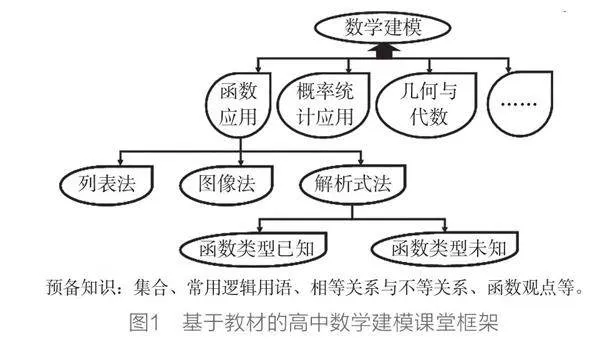
实际问题一直是数学发展的重要源泉，解决实际问题也是数学价值的重要体现。数学建模是对现实问题进行数学抽象，从现实生活中发现问题并提出问题，用数学语言分析问题并建立模型，用数学方法构建模型解决问题的过程，确定参数并计算求解，将结果带入现实对象验证结果并改进模型（见图2）。

学生通过各种类型的函数应用题初步具备将实际问题分析抽象转化为数学模型即建立数学模型的能力，初步具备了数学推演建模的能力，初步具备了将数学结果还原到实际问题中去检验、解释实际问题的能力。数学建模与函数应用题最大的区别在于解决方法不唯一。它往往求不出问题的准确解，而是给出解决问题的可以不断优化的方法，因而需要将数学结果带回到实际问题中，验证是不是符合现实对象的要求。

在培养数学建模能力的过程中，教师应密切关注学生的数学表达，包括文字语言、符号语言和图形语言的表达。学生在处理数学问题时的有效表达会促进其对问题的深入思考，有效表达也可以作为深入思考的表现性证据。

数学建模活动可促进数学知识的掌握与应用，让学生感觉到数学的用途，真正地把数学用起来。案例能很好地融合提升传统数学课堂知识能力，在我们的数学建模模式中，将建模案例归类到第二阶段的建模培养，能让学生充分体验数学建模的全过程，是学生从传统数学课堂到数学建模过渡的重要途径。做好数学应用的梳理、总结、提升，做好案例的开发，可以更好地实现核心素养下的高中数学建模的落地。

本文系北京市教育科学“十三五”规划课题“新课程标准下高中数学课堂中的数学建模教学实践探究”（课题批准号：CDCA2020109）研究成果。

（作者单位：1、2.北京市第三十五中学；3.北京市西城教育研修学院）

责任编辑：赵继莹