基于旋转粒化的逻辑回归算法
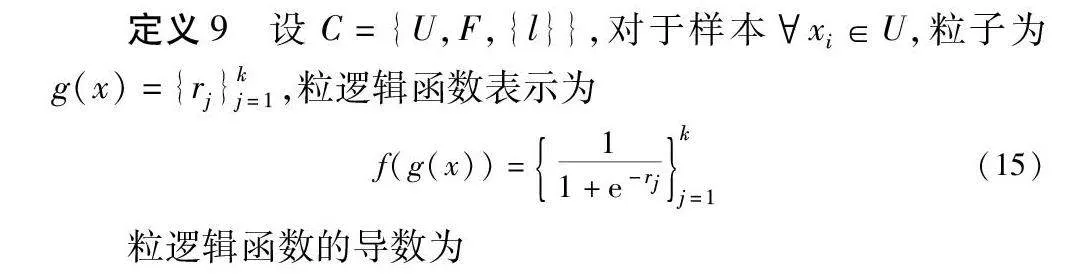








摘 要:逻辑回归(LR)作为监督学习的二元分类广义线性分类器,在处理线性数据方面表现出结构简单、解释性强,拟合效果好的特点。然而,当面对高维、不确定性和线性不可分数据时,逻辑回归的分类效果受到限制。针对逻辑回归的固有缺陷,引入粒计算理论,借助粒化的优势提出一种新型的逻辑回归模型:旋转粒逻辑回归。通过引入旋转粒化理论,在特征两两组合形成的平面坐标系上旋转不同角度,构建旋转粒子,多平面坐标系上粒化构造旋转粒向量。进一步定义粒的大小、度量和运算规则,提出旋转粒逻辑回归的损失函数。通过求解损失函数,得到旋转粒逻辑回归的优化解。最后,采用多个UCI数据集进行实验,从多个评价指标比较的结果表明旋转粒逻辑回归模型的有效性。
关键词:逻辑回归; 粒计算; 向量旋转; 粒逻辑回归; 损失函数
中图分类号:TP181 文献标志码:A
文章编号:1001-3695(2024)08-021-2398-06
doi:10.19734/j.issn.1001-3695.2023.11.0578
Logistic regression algorithm based on rotating granulation
Kong Liru1, Chen Yuming1, Fu Xingyu1, Jiang Hailiang1, Xu Jincheng2
(1.College of Computer & Information Engineering, Xiamen University of Technology, Xiamen Fujian 361024, China; 2.Xiamen Wanyin Intelligent Technology Co., Ltd., Xiamen Fujian 361024, China)
Abstract:LR serves as a generalized linear classifier for binary classification in supervised learning, exhibiting characteristics of simplicity in structure, strong interpretability, and effective fitting when dealing with linear data. However, its classification performance becomes limited when confronted with high-dimensional, uncertain, and linearly inseparable data. To address the inherent limitations of logistic regression, this paper introduced the theory of granular computing and proposed a novel logistic regression model called rotating granular logistic regression(RGLR). This paper introduced the theory of rotating granulation, where different angles of rotation were applied to pairs of features forming a plane coordinate system. This process constructed rotating granules by rotating pairs of features at various angles on the plane coordinate system, and granulated to form rotating granule vectors on multiple plane coordinate systems. This paper further defined the size, measurement, and operational rules of granules, and proposed a loss function for rotating granular logistic regression. The optimized solution of the rotating granular logistic regression was obtained by solving the value of the loss function. Finally, experiments are conducted using multiple UCI datasets, and the results compared across various evaluation metrics, indicate the effectiveness of the rotating granular logistic regression model.
Key words:logistic regression; granular computing; rotating vector; rotating granular logistic regression; loss functions
0 引言
模糊集和模糊计算概念由美国学者Zadeh[1]在1965年提出,模糊集通过隶属函数表示元素和集合之间的关系。1996年Lin等人[2]首次提出粒计算理论。粒计算强调事物多层次、多粒度表示,使用新的表示方法对复杂知识做新表示,处理不确定性数据。加拿大院士Pedrycz提出多种粒分类[3]和粒聚类算法[4]。1997年,Zadeh[5]指出,模糊逻辑和人类推理能力是相似的,模糊信息粒化基于人类推理方法去粒化信息。除了模糊信息粒化,还有很多粒化方法,如粗糙集粒化和阴影集粒化。文献[6]总结并讨论不同条件下的粒化方法。进入21世纪后,国内越来越多的学者投身到粒计算的研究中。Lin等人[7,8]成功将粒计算应用到知识发现和数据挖掘领域。文献[9,10]通过定义邻域关系构建邻域粒化。文献[11~13]基于粒计算理论阐述不确定性,并将信息熵引入粒计算领域。Yu等人[14]提出多粒度融合学习来学习不同粒度模式下的决策。2014年,Qian等人[15]设计出一种并行属性近似算法,以提高属性近似问题的粒计算操作效率。文献[16]提出基于概念格的粒度结构,并应用于概念分析中。Chen等人[17]从集合和向量的角度定义了粒的结构,并进一步研究粒的不确定性和距离度量。Li等人[18]将提升算法与粒KNN算法集成,进一步提高KNN算法的性能。粒计算是一种从人类认知的角度定义的算术模型,与人类的逻辑、认知和记忆高度相似,粒计算能够分析与处理复杂数据,将复杂的对象细粒度分解而求解问题,并广泛应用于机器学习领域[19~23]。
逻辑回归是一种数学模型,可以估计属于某一类的概率。在数据科学中,逻辑回归是一种分类方法[24]。许多研究者在工程领域使用了回归模型,并开展了出色的研究工作,如健康科学[25]、文本挖掘[26]和图像分析[27]。然而,传统的逻辑回归方法只能从当前的样本特征中学习。但数据集中多个独立样本的特征之间仍存在一些联系,这被传统的逻辑回归方法所忽视。当数据维度过高时,逻辑回归分类器可能会出现退化现象。粒化处理可以通过引入粒计算使分类过程具有结构化和层次化,从而提高了数据分类[28]的准确性和鲁棒性。
本文利用粒计算处理模糊、不确定性数据的优势以及逻辑回归在处理二元分类问题时具有良好性能的特点将粒计算和逻辑回归相结合,两者结合有助于更全面地处理复杂数据,提出一种旋转粒逻辑回归方法。该方法基于粒计算理论,通过建立特征点平面坐标系,在特征点平面坐标系上旋转多个角度对样本进行旋转粒化,形成旋转粒子,多平面坐标系上的粒化构造成旋转粒向量。进一步定义粒的大小、度量和运算规则,提出粒逻辑回归的损失函数。将逻辑回归的思想和粒计算理论相结合提出粒逻辑回归算法。使用UCI数据集进行实验测试表明,本文算法得到的分类效果优于传统逻辑回归算法,为分类算法探索一条新的途径。
1 粒向量与粒化
首先将特征归一化并且将样本粒化成多个粒子。通过定义粒和粒度计算,将粒化后的粒子输入到旋转粒逻辑回归模型中,输出样本预测标签,具体步骤介绍如下。
1.1 粒化
粒计算是处理不确定性信息的有效工具。设C={U,F,{l}}为一分类系统,其中U={x1,x2,…,xn}为样本集合,F={f1,f2,…,fh}为样本特征集合,{l}为样本的类别标签;给定单样本x∈U,对于单特征f∈F,v(x,f)∈[0,1]表示样本x在特征f上归一化后的值;该样本x对应的标签值为y∈{0,1}。
定义1 设h维特征集为F={f1,f2,…,fh},任意选取两个特征fa,fb∈C进行组合,形成特征点平面坐标系〈fa,fb〉或〈fb,fa〉,其中第一个元素为横坐标,第二个元素为纵坐标。以下本文只考虑这种情况〈fa,fb〉,其中fa为横坐标,fb为纵坐标。
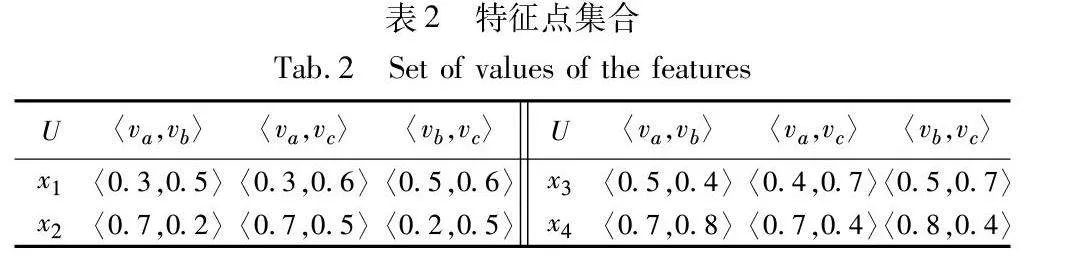
对于给定样本x∈U,其在特征点平面坐标系〈fa,fb〉中的值为〈v(x,fa),v(x,fb)〉,简写为〈va,vb〉。h维特征集F={f1,f2,…,fh}中,所有特征两两组合,则形成了特征点平面坐标系集合,含有h×(h-1)/2个平面坐标系。对于给定样本x∈U,所有特征值两两组合,则形成了h×(h-1)/2个平面特征点值。
定义2 设特征点平面坐标系为〈fa,fb〉,对于平面中任意点v=(va,vb)T,按照逆时针旋转θ角度,形成新的特征点为v′=Rθ*v,其中Rθ=cos θ-sin θsin θcos θ。
定义3 给定数据集C={U,F,{l}},对于任一样本x∈U,其在特征点平面坐标系〈fa,fb〉的值为v=(va,vb)T,则x在该平面坐标系上进行旋转粒化,形成的旋转粒子定义为
gv(x)={gv(x)jθ}kj=1={rj}kj=1={r1,r2,…,rk}(1)
其中:gv(x)是一个集合;rj是集合中的一个元素,rj=Rjθ*v表示样本x在特征点平面坐标系〈fa,fb〉上旋转jθ角度后的点。定义gv(x)为旋转粒子,gv(x)j为粒子gv(x)的第j个粒核。粒子由粒核组成,是一个有序集合,其元素是平面上的点;因此,旋转粒子也是点的有序集合。
样本x在决策特征l上进行扩展粒化,形成标签粒子,定义为
gl(x)={gl(x)j}kj={l}kj=1(2)
其中:l为样本x的标签值。在逻辑回归分类器中,标签值为0和1。
定义4 设C={U,F,{l}}为数据集,对于任一样本x∈U,从特征集F中任选特征组合成m个平面坐标系,构成集合为P={v1,v2,…,vm},其中va=〈fax,fay〉,则x在特征点平面坐标系集P上的旋转粒向量定义为
GP(x)=(gv1(x),gv2(x),…,gvm(x))T(3)
其中:gvm(x)是样本x在特征点平面坐标系vm上的旋转粒子。因va=〈fax,fay〉,所以旋转粒向量可表示为
GP(x)=(gf1x(x),gf1y(x),gf2x(x),gf2y(x),…,gfmx(x),gfmy(x))T(4)
为方便计算,则旋转粒向量表示为
G(x)=(g1(x),g2(x),…,g2m(x))T(5)
粒向量G(x)由粒子组成,而粒子是一个有序集合的形式。因此,粒向量的元素是有序的集合,与传统向量不一样,传统向量的元素是一个实数。
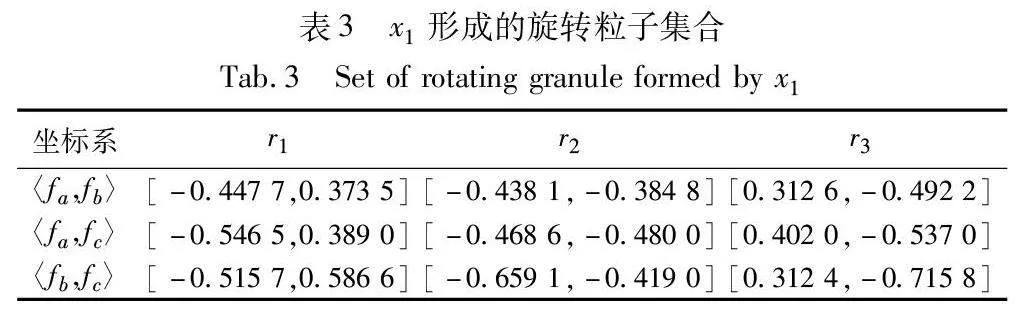
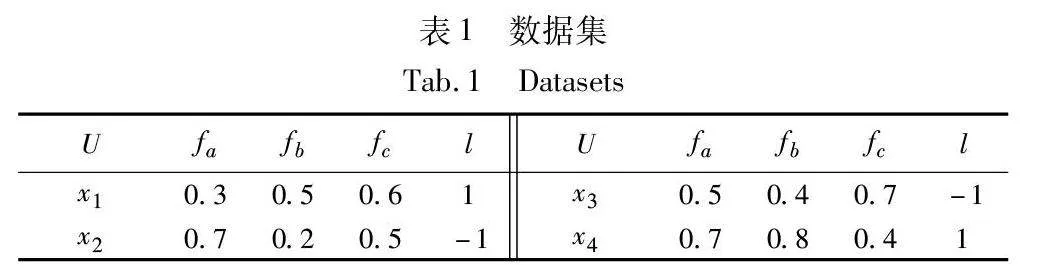
例1 数据集C={U,F,{l}}如表1所示,U={x1,x2,x3,x4}为样本集合,F={fa,fb,fc}为特征集合,l为类别标签,设旋转角度θ为30°,旋转次数为三次。数据集如表1所示。
特征集F={fa,fb,fc},若选取两个特征fa,fb∈F进行组合,形成特征点平面坐标系〈fa,fb〉或〈fb,fa〉,其中第一个元素为横坐标,第二个元素为纵坐标。以下本文只考虑〈fa,fb〉这种情况,其中fa为横坐标,fb为纵坐标。
对于给定样本x1∈U,其在特征点平面坐标系〈fa,fb〉中的值为〈v(x1,fa),v(x1,fb)〉,简写为〈va,vb〉。三维特征集F={fa,fb,fc}中,所有特征两两组合,则形成特征点平面坐标系集合,含有三个平面坐标系。同时形成三个平面特征点值。样本特征点集合如表2所示。
对于平面中任意点v=(va,vb)T,按照逆时针旋转θ=30°,形成新的特征点为:v′=Rθ*v,其中Rθ=cos30°-sin30°sin30°cos30°。则x1在该平面坐标系上进行三次旋转粒化,形成的旋转粒子为gv(x1)={gv(x1)jθ}3j=1={rj}3j=1={r1,r2,r3},x1在各特征点平面坐标系形成的旋转粒子集合如表3所示。
表3中每一行粒核r1、r2、r3组合形成x1在该平面上的旋转粒子gv(x1)。则x1在特征点平面坐标系集P上的所有粒子组合形成的旋转粒向量为
GP(x)=(gv1(x),gv2(x),gv3(x))T
1.2 粒子的运算
定义5 设g={sj}kj=1,f={tj}kj=1为两个粒子,则两个粒子的加、减、乘、除运算定义为
g+f={sj+tj}kj=1(6)
g-f={sj-tj}kj=1(7)
g×f={sj×tj}kj=1(8)
g/f={sj/tj}kj=1(9)
定义6 设粒向量为G(xi)=(g1(xi),g2(xi),…,gm(xi))T,G(xk)=(g1(xk),g2(xk),…,gm(xk))T,则这两个粒向量的点乘为
G(xi)·G(xk)=G(xi)TG(xk)=g1(xi)*g1(xk)+
g2(xi)*g2(xk)+…+gm(xi)*gm(xk)(10)
两个粒向量的点乘结果为一个粒子。因此,本文可以通过构造一个权值粒向量,让样本的粒向量与权值粒向量进行点乘运算,其结果也为一个粒子。
定义7 设粒子为gc(x)={rj}kj=1,其大小定义为
q(gc(x))=∑kj=1rj(11)
若q(gc(x))>0,则粒子大小为正;反之,粒子大小为负。
粒逻辑回归分类模型的学习训练过程就是优化确定权值粒向量与偏置粒子的值,预测样本类别则通过学习得到的粒逻辑回归模型来分类。对于输入的样本进行粒化和粒逻辑回归模型计算后,输出粒子,通过度量粒子的大小确定样本的类别。输出结果为正,则判定为正例类别;输出结果为负,则判定为负例类别。
定义8 设m维粒向量为G(xi)=(g1(xi),g2(xi),…,gm(xi))T,则粒向量的范粒子定义为
a)粒向量-1范粒子。
‖G(xi)‖1=∑mj=1gj(xi)(12)
b)粒向量-2范粒子。
‖G(xi)‖2=∑mj=1gj(xi)*gj(xi)=G(xi)·G(xi)(13)
c)粒向量-p范粒子。
‖G(xi)‖p=(∑mj=2gpj(xi))1p(14)
粒向量范粒子运算的结果是粒子。范粒子运算提供了一种从粒向量转换为粒的方法。
2 粒逻辑回归算法
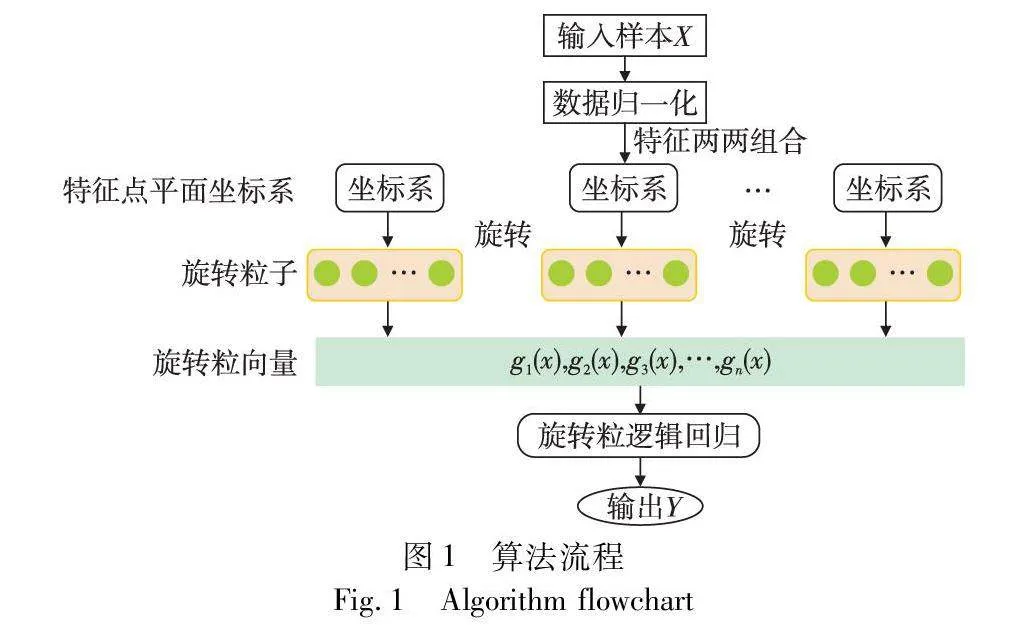
为了构建旋转粒逻辑回归系统,本文首先定义了旋转粒逻辑函数。算法流程如图1所示。
定义9 设C={U,F,{l}},对于样本xi∈U,粒子为g(x)={rj}kj=1,粒逻辑函数表示为
f(g(x))=11+e-rjkj=1(15)
粒逻辑函数的导数为
f′(g(x))=ddrjf(rj)kj=1=11+e-rj1-11+e-rjkj=1(16)
逻辑回归是一个线性分类模型。为了得到粒逻辑回归模型,需要导入粒线性方程。文献[21,22]定义了粒状线性回归模型。
定义10 设C={U,F,{l}},对于样本xi∈U,粒向量为G(xi)=(g1(xi),g2(xi),…,gm(xi))T,权值粒向量W=(w1,w2,…,wm,b)T,粒回归方程定义为
Reg(x)=W·G(x)=w1×g2(x)+w2×g2(x)+…+wm×gm(x)+1×b(17)
将粒线性回归应用于粒度逻辑函数,得到粒度逻辑回归模型。
定义11 设C={U,F,{l}},粒向量为G(x),权值粒向量W,粒逻辑回归如下所示。
fRGLR(x)=f(Reg(x))=11+e-W·G(x)kj=1(18)
旋转粒逻辑回归是关于粒子的函数,通过样本条件粒向量与权值粒向量的内积计算,结果为决策粒子。同时,标签值进行粒化后形成标签粒子。因此,条件粒子与决策粒子进行比较,将其差异按照梯度方向回传修正权值粒核向量,从而形成旋转粒逻辑回归分类器。
2.1 粒逻辑回归损失函数
粒逻辑回归模型中,输入是一个样本的旋转粒向量,输出是一个决策粒子,决策粒子可以与构成粒损失函数的标签粒子进行比较。为了优化粒逻辑回归模型的参数,需要定义其损失函数。
定义12 给定训练数据集T={(x1,y1),(x2,y2),…,(xn,yn)},其中xi为h维特征向量,xi∈XRh,yi∈{0,1},i=1,2,…,n。训练集T粒化为GT={(G(x1),g(y1)),(G(x2),g(y2)),…,(G(xn),g(yn))},其中G(xi)=(g1(xi),g2(xi),…,gh(xi))T为粒向量,g(yi)为标签粒子。粒逻辑回归的损失函数定义为
L(g(yi),fRGLR(G(xi)))=-1n
∑ni=1[g(yi)log(fRGLR(G(xi)))+(1-g(yi))log(1-fRGLR(G(xi)))](19)
其中:1为1-粒子。
2.2 粒逻辑回归算法
算法1 旋转粒逻辑回归学习算法
输入:训练集T={(x1,y1),(x2,y2),…,(xn,yn)},其中xi为h维特征向量,其中xi∈XRh;yi是l-维标签向量,yi∈YRl,i=1,2,…,n;学习率为η(0<η≤1)。
输出:W,b。
a)训练集T旋转粒化为
GT={(G(x1),g(y1)),(G(x2),g(y2)),…,(G(xn),g(yn))};
b)构建旋转粒逻辑回归模型,并随机初始化权值粒向量W=(w1,w2,…,wm)T和偏置粒子b;
c)将粒向量输入旋转粒逻辑回归模型,得到决策粒子;
d)计算决策粒子和标签粒子的损失函数L,根据梯度方向,反向传播修正权重粒向量和偏置粒子;
e)步骤c)d)循环多次,直至损失函数收敛或迭代达到最大次数;
f)输出权值粒向量W=(w1,w2,…,wm)T和偏置粒子b。
3 实验分析
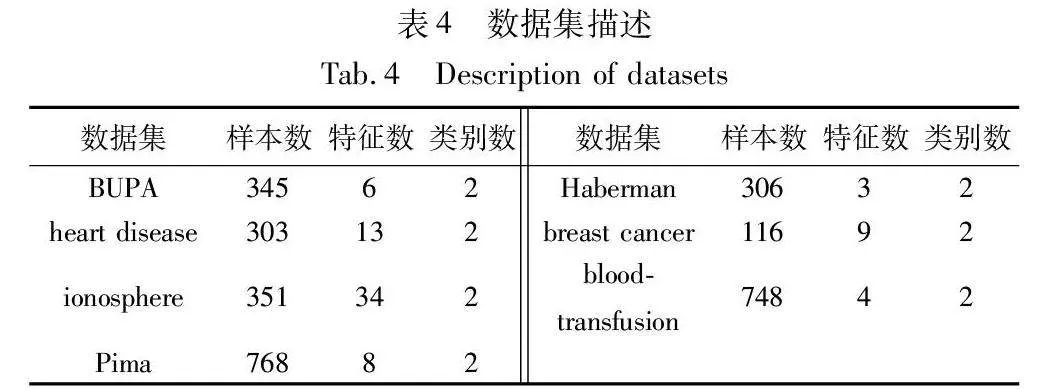
实验采用BUPA、heart disease、ionosphere、Pima、Haberman、breast cancer、blood-transfusion七个UCI数据集来验证本文算法的有效性,具体描述如表4所示。
由于每个数据集的特征值域是不同的,所以要对粒化后的粒子采用最大最小值归一化,将每个特征的值域转为[0,1],最大最小值归一化公式为
Xnorm=X-XminXmax-Xmin(20)
使用accurancy、F1-score、ROC曲线、AUC四个指标作为评估指标,其中,准确率,F1-score表达式如下:
accuracy=TP+TNTP+TN+FP+FN(21)
precision(P)=TPTP+FP(22)
recall(R)=TPTP+FN(23)
F1=2×P×RP+R(24)
为了测试算法的有效性,分别采用传统逻辑回归模型、基于旋转粒化的逻辑回归模型在不同数据集上进行旋转,对不同旋转次数的准确率做对比。同时采用十折交叉验证进行实验,将每个数据集随机分成10份,其中一份为测试集,其余为训练集。再选另一份为测试集,其余为训练集,共测试10次,分类精度为10次的平均值。
3.1 旋转次数的影响
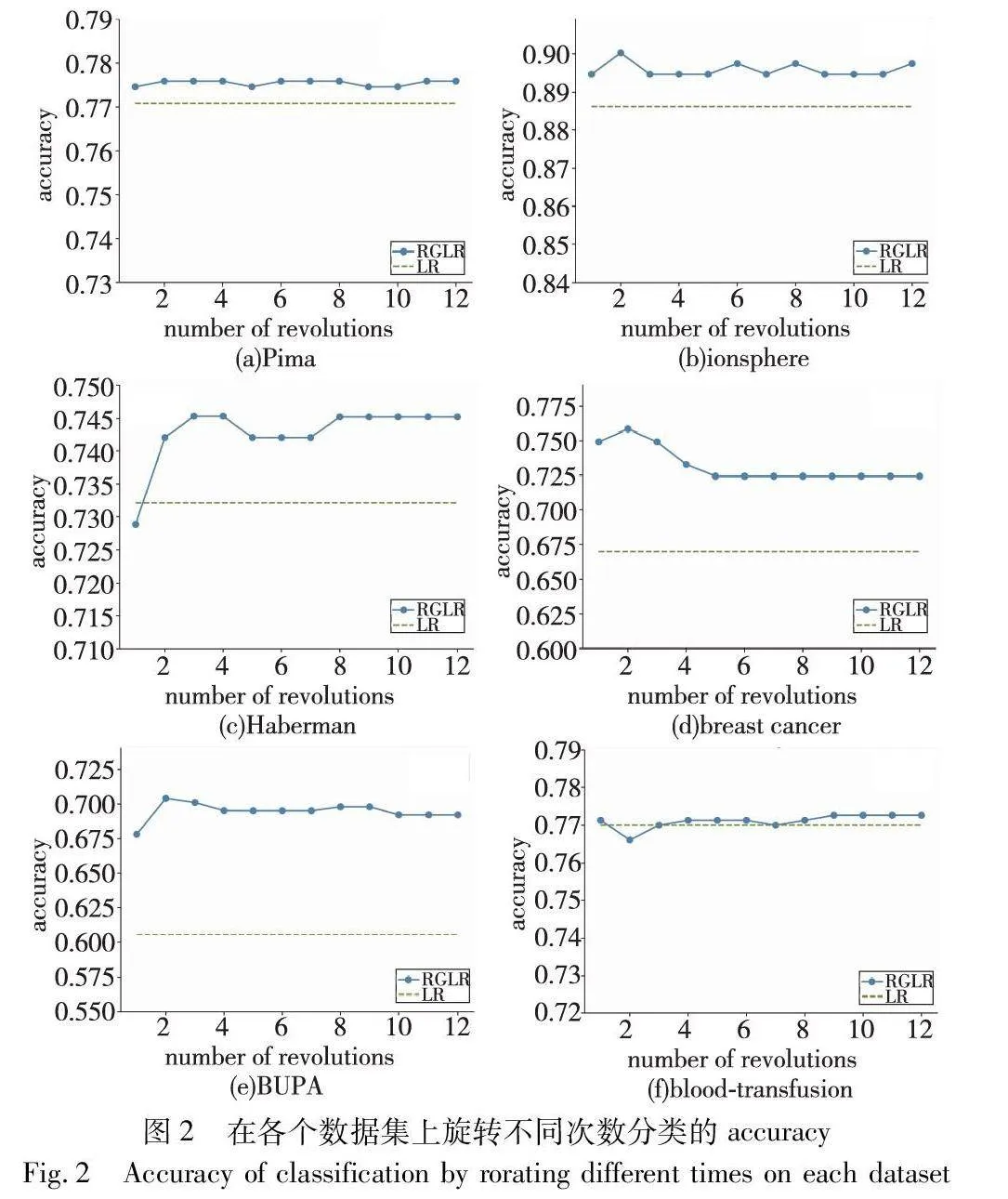
旋转粒化过程需要设置旋转角度与旋转次数的参数,实验中设置粒化角度θ为30°,旋转次数为1~12。本节实验主要测试旋转粒化次数参数的影响。七个UCI数据集的结果取六个(包括Pima、ionosphere、Haberman、breast cancer、BUPA、blood-transfusion),实验结果如图2所示。
由图2可知,旋转粒逻辑回归(RGLR)算法的accuracy在Pima、ionosphere、breast cancer、BUPA数据集上始终高于经典逻辑回归算法(LR)。在Pima数据集中,RGLR的准确率始终高于LR,准确率之差为0.003 9~0.005 20。在ionosphere数据集中,当旋转次数达到2时,RGLR的准确率达到峰值0.894 5且始终高于LR算法。在Haberman数据集中,RGLR的准确率曲线随准确率先上升后保持平稳,当旋转次数为1时,RGLR的准确率为0.728 9,低于LR,但在旋转2~12次时,RGLR的准确率始终高于LR,准确率之差为0.009 8~0.013 2。在breast cancer数据集中,RGLR的准确率曲线始终高于LR,且在旋转次数为2时达到峰值0.758 3,准确率之差为0.054 5~0.088 6。在BUPA数据集中,RGLR的准确率曲线始终高于LR,准确率之差为0.086 5~0.098 4。在blood-transfusion数据集中,当旋转次数为2时,RGLR的准确率低于LR,在其他旋转次数时,RGLR的准确率比LR略高或相等。
从旋转次数上看,对于不同数据分布的数据集、不同的旋转次数都会对最终分类性能造成影响,且并非旋转次数越多,分类性能越好。从总体上看,除了blood-transfusion数据集,RGLR算法的accuracy均高于LR,均能找到合适的旋转次数使得accuracy达到最高值,超过经典LR算法。与LR算法相比,RGLR算法在算法进行之前就预先对数据进行粒化,利用旋转粒向量使得算法对特征信息少的数据分类性能提高。
3.2 分类算法比较
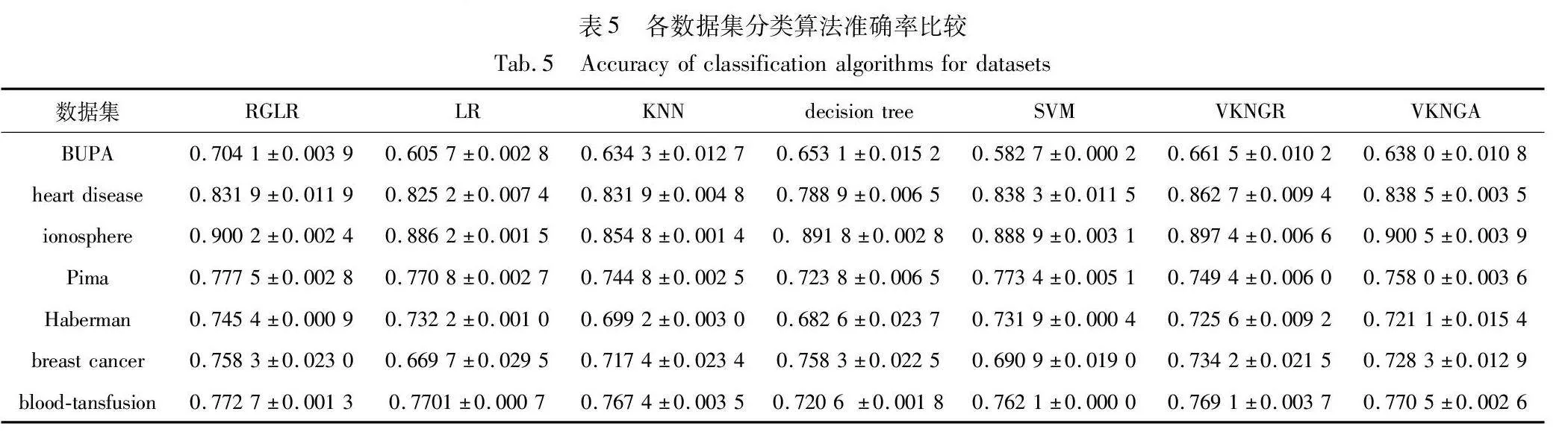
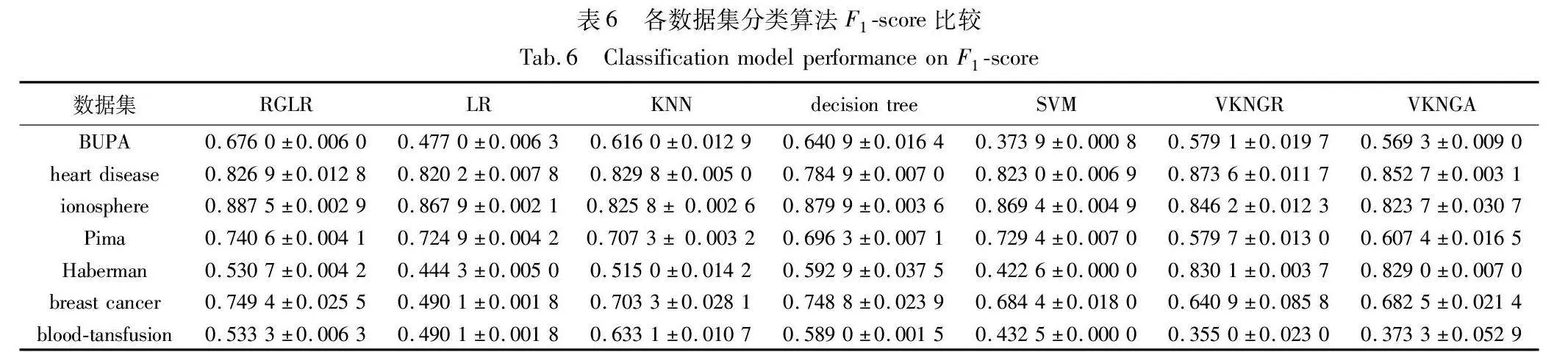
经典的机器学习模型有K近邻、决策树、SVM等。本文采用准确率、F1-score来评价预测算法的性能。对比了LR、K近邻、决策树、SVM以及基于粒向量的K近邻分类器[29],其中基于粒向量的K近邻分类算法包括基于相对粒向量距离的K近邻分类器(VKNGR)和基于绝对粒向量距离的K近邻分类器(VKNGA)。数据集中使用十次交叉验证求均值的方法得出均值和方差。各分类算法准确率如表5所示,各分类算法F1-score比较如表6所示,结果保留四位小数。
从实验中可以得出,RGLR算法在BUPA、Pima、Haberman、breast cancer、blood-transfusion数据集上要明显优于其他算法。除在heart disease、ionosphere数据集上准确率相对较低,在其他数据集上与其他算法相比,大部分情况准确率更高。
由表5可知,当使用accuracy作为性能评估指标时,在BUPA、Pima、Haberman和blood-tansfusion数据集中RGLR算法的得分要高于其他六种算法的得分。在breast cancer数据集中, RGLR算法的得分与决策树得分相同且比经典LR算法高出0.088 6。在heart disease数据集中RGLR算法得分虽然大于LR算法的得分,但低于VKNGR的得分。在ionosphere数据集中RGLR准确率得分略低于拥有最高得分的VKNGA算法。
由表6可知,当使用F1-score作为性能评估指标时,在BUPA、ionosphere、Pima和breast cancer数据集中,RGLR的F1-Score高于其他六种算法的F1-score得分,在数据集heart disease和Haberman上,VKNGR F1-score高于包括RGLR在内的其他六种算法的F1-score,在blood-transfusion数据集中,KNN的F1-score高于其他六种算法的F1-score。
3.3 ROC曲线对比
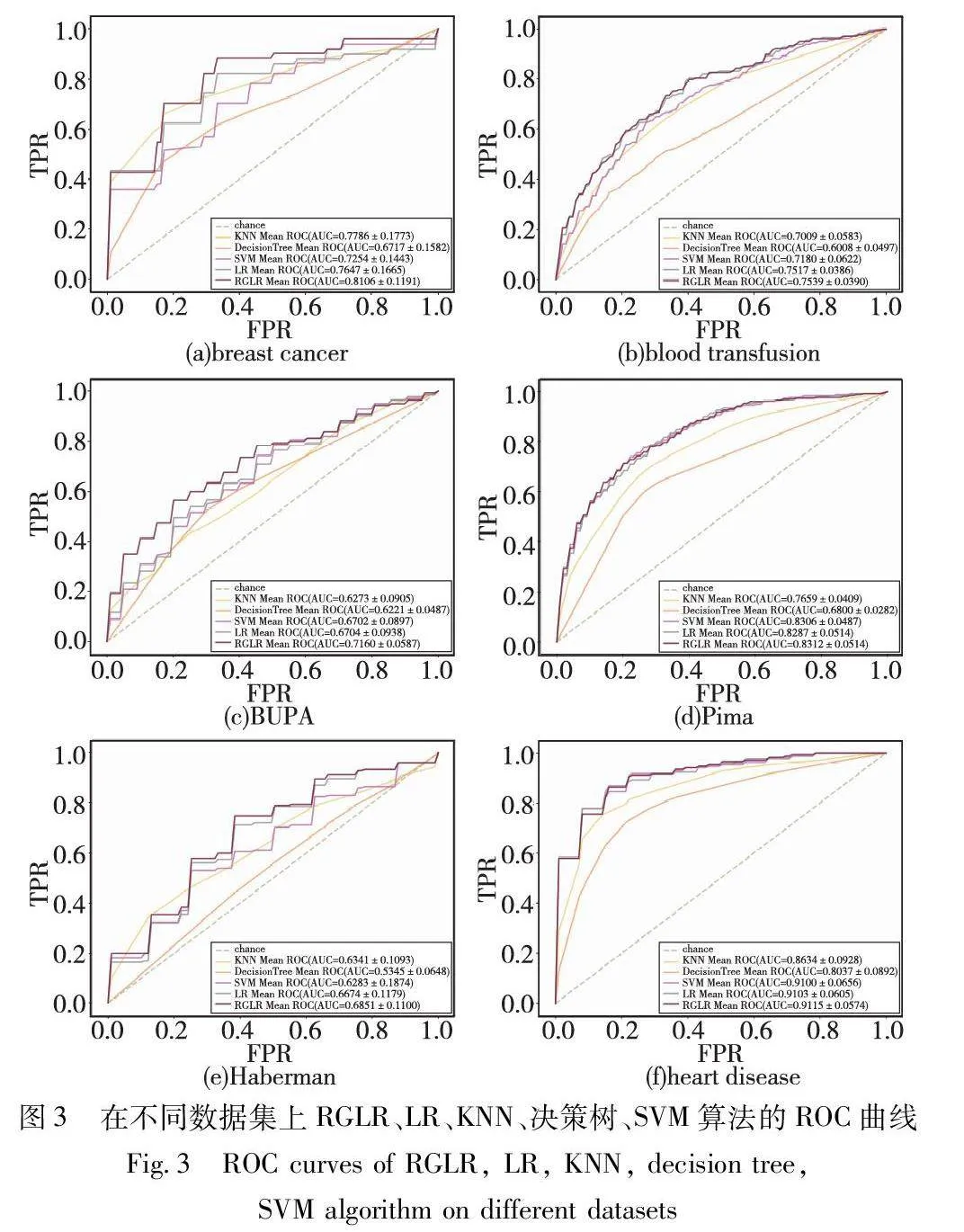
RGLR、LR、KNN、决策树和SVM在七个UCI数据集的结果取六个数据集(包括breast cancer、blood-transfusion、BUPA、Pima、Haberman和heart disease)进行十折交叉验证的接受者操作特性ROC曲线如图3所示。
由图3可知,在同一数据集上,不同的分类算法ROC曲线不同。在ROC曲线中,偏离对角线表现出更好的性能。在breast cancer、blood-transfusion、BUPA和Haberman 数据集上RGLR的ROC曲线明显更靠近左上角,其AUC值最高,表明RGLR的分类效果更好。在Pima和heart disease数据集上RGLR、LR和SVM三种算法的ROC曲线接近,但RGLR的AUC值最高,表明RGLR的分类效果更好。
从以上实验可知,在大部分数据集上旋转粒逻辑回归算法的分类性能均优于逻辑回归算法,优于大部分的其他算法。与传统算法不同,旋转粒逻辑回归算法利用旋转粒化技术在结构上突破,引入了更为复杂的特征表示和模型的非线性建模能力,同时在不同角度和方向上引入了新的特征变换,这不仅提高了对高维数据集的适应能力,还能够捕捉到数据中更加复杂的模式和结构,且提升了算法的分类性能,使得算法对于不同类型的数据集都有一个不错的效果。
4 结束语
传统逻辑回归分类器不具备处理模糊数据的性能,对于难以处理的YF3nzPUO1phk6pBKtjf00Q==高维、不确定性数据,其分类效果不佳。本文从样本的粒化角度出发,通过定义粒向量的形式,还提出了一种新型的逻辑回归分类模型:旋转粒逻辑回归。通过引入粒计算理论,样本在特征构成的平面坐标系上不同角度的旋转,构建旋转粒子,多平面坐标系上的粒化构造成旋转粒向量。进一步定义旋转粒的大小、度量和运算规则,提出粒逻辑回归的损失函数。最后,进行实验分析,验证了旋转粒K近邻模型的正确性与有效性。在未来的工作中,可以研究粒的局部粒化方法,提高粒化速度与粒化性能;可以研究粒的度量方法,提高粒分类器的分类精度。
参考文献:
[1]Zadeh L A. Fuzzy sets[J]. Information and Control, 1965,8(3): 338-353.
[2]Lin T Y. Granular computing on binary relations I: data mining and neighborhood systems[J]. Rough Sets in Knowledge Discovery, 1998, 2: 165-166.
[3]Fu Chen, Lu Wei, Pedrycz W, et al. Fuzzy granular classification based on the principle of justifiable granularity[J]. Knowledge-Based Systems, 2019, 170: 89-101.
[4]Zhou Yanjun, Ren Huorong, Li Zhiwu, et al. Anomaly detection based on a granular Markov model[J]. Expert Systems with Applications, 2022, 187: 115744.
[5]Zadeh L A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J]. Fuzzy Sets and Systems, 1997, 90(2): 111-127.
[6]Lu Wei, Ma Cong, Pedrycz W, et al. Design of granular model: a method driven by hyper-box iteration granulation[J]. IEEE Trans on Cybernetics, 2023, 53(5): 2899-2913.
[7]Lin T Y. Approximate computing in numerical analysis variable interval computing[C]//Proc of IEEE International Conference on Systems, Man and Cybernetics. Piscataway, NJ: IEEE Press, 2019: 2013-2018.
[8]Lin T Y, Zadeh L A. Special issue on granular computing and data mining[J]. International Journal of Intelligent Systems, 2004, 19(7): 565-566.
[9]Yue Xiaodong, Zhou Jie, Yao Yiyu, et al. Shadowed neighborhoods based on fuzzy rough transformation for three-way classification[J]. IEEE Trans on Fuzzy Systems, 2020, 28(5): 978-991.
[10]Zhan Jianming, Zhang Xiaohong, Yao Yiyu. Covering based multigranulation fuzzy rough sets and corresponding applications[J]. Artificial Intelligence Review, 2020, 53(2): 1093-1126.
[11]Gao Can, Zhou Jie, Miao Duoqian, et al. Granular-conditional-entropy based attribute reduction for partially labeled data with proxy labels[J]. Information Sciences, 2021, 580: 111-128.
[12]Zhang Xianyong, Gou Hongyuan, Lyu Zhiying, et al. Double-quanti-tative distance measurement and classification learning based on the tri-level granular structure of neighborhood system[J]. Knowledge-Based Systems, 2021, 217: 106799.
[13]Zhang Xianyong, Yao Hong, Lyu Zhiying, et al. Class-specific information measures and attribute reducts for hierarchy and systematicness[J]. Information Sciences, 2021, 563: 196-225.
[14]Yu Ying, Tang Hong, Qian Jin, et al. Fine-grained image recognition via trusted multi-granularity information fusion[J]. International Journal of Machine Learning and Cybernetics, 2023, 14(4): 1105-1117.
[15]Qian Jin, Miao Duoqian, Zhang Zehua, et al. Parallel attribute reduction algorithms using mapreduce[J]. Information Sciences, 2014, 279: 671-690.
[16]Shao Mingwen, Wu Weizhi, Wang Xizhao, et al. Knowledge reduction methods of covering approximate spaces based on concept lattice[J]. Knowledge-Based Systems, 2020, 191: 105269.
[17]Chen Yumin, Qin Nan, Li Wei, et al. Granule structures, distances and measures in neighborhood systems[J]. Knowledge-Based Systems, 2019, 165: 268-281.
[18]Li Wei, Chen Yumin, Song Yuping. Boosted K-nearest neighbor classifiers based on fuzzy granules[J]. Knowledge-Based Systems, 2020, 195: 1-13.
[19]Xia Shuyin, Liu Yunsheng, Ding Xin, et al. Granular ball computing classifiers for efficient, scalable and robust learning[J]. Information Sciences, 2019, 483: 136-152.
[20]陈玉明, 董建威. 基于粒计算的非线性感知机[J]. 数据采集与处理, 2022, 37(3): 566-575. (Chen Yuming, Dong Jianwei. Non-linear perceptron based on granular computing[J]. Journal of Data Acquisition and Processing, 2022, 37(3): 566-575.)
[21]Chen Linshu, Shen Fuhui, Tang Yufei, et al. Algebraic structure based clustering method from granular computing prospective[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2023, 31(1): 121-140.
[22]Chen Linshu, Zhao Lei, Xiao Zhenguo, et al. A granular computing based classification method from algebraic granule structure[J]. IEEE Access, 2021, 9: 68118-68126.
[23]Mendel J M, Bonissone P P. Critical thinking about explainable AI(XAI) for rule-based fuzzy systems[J]. IEEE Trans on Fuzzy Systems, 2021, 29(12): 3579-3593.
[24]Nibbering D, Hastie T J. Multiclass-penalized logistic regression[J]. Computational Statistics & Data Analysis, 2022, 169: 107414.
[25]Jawa T M. Logistic regression analysis for studying the impact of home quarantine on psychological health during COVID-19 in Saudi Arabia[J]. Alexandria Engineering Journal, 2022, 61(10): 7995-8005.
[26]Li Chenggang, Liu Qing, Huang Lei. Credit risk management of scientific and technological enterprises based on text mining[J]. Enterprise Information Systems, 2021, 15(6): 851-867.
[27]张旭, 柳林, 周翰林, 等. 基于贝叶斯逻辑回归模型研究百度街景图像微观建成环境因素对街面犯罪的影响[J]. 地球信息科学学报, 2022, 24(8): 1488-1501. (Zhang Xu, Liu Lin, Zhou Hanlin, et al. Using Baidu street view images to assess impacts of micro-built environment factors on street crimes: a Bayesian logistic regression approach[J]. Journal of Geoinformation Science, 2022, 24(8): 1488-1501.)
[28]Chen Yumin, Cai Zhiwen, Shi Lei, et al. A fuzzy granular sparse learning model for identifying antigenic variants of influenza viruses[J]. Applied Soft Computing, 2021, 109: 107573.
[29]陈玉明, 李伟. 粒向量与K近邻粒分类器[J]. 计算机研究与发展, 2019, 56(12): 2600-2611. (Chen Yuming, Li Wei. Granular vectors and K-nearest neighbor granular classifiers[J]. Journal of Computer Research and Development, 2019, 56(12): 2600-2611.)

