基于分区搜索和强化学习的多模态多目标头脑风暴优化算法






摘 要:维持种群多样性和提高算法搜索效率是多模态多目标优化亟需解决的两大问题。为解决以上问题,提出了一种基于分区搜索和强化学习的多模态多目标头脑风暴优化算法(MMBSO-ZSRL)。在MMBSO-ZSRL中,首先将决策空间分解为多个子空间以降低搜索难度和维持种群多样性;然后,使用SARSA(state-action-reward-state-action) 算法来平衡头脑风暴算法的全局探索和局部开发能力;并使用特殊拥挤距离来挑选个体来指导种群进化。为了验证所提算法的性能,选取六种先进的多模态多目标优化算法来进行比较,并选取IEEE CEC2019多模态多目标问题基准测试集来对所有比较算法的性能进行测试。实验结果表明,MMBSO-ZSRL的整体性能要显著优于其他六种比较算法。MMBSO-ZSRL不仅可以找到多样性和逼近性更好的帕累托前沿,而且可以在决策空间找到更多的帕累托最优解。
关键词:多模态多目标优化; 头脑风暴优化算法; 强化学习; SARSA算法; 分区搜索
中图分类号:TP301.6 文献标志码:A
文章编号:1001-3695(2024)08-018-2374-10
doi:10.19734/j.issn.1001-3695.2023.12.0588
Multimodal multi-objective brain storm optimization algorithm based onzoning search and reinforcement learning
Li Xin1, Yu Moduo2, Jiang Qingchao3, Fan Qinqin1
(1.Logistics Research Center, Shanghai Maritime University, Shanghai 201306, China; 2.Key Laboratory of Control of Power Transmission & Conversion(Ministry of Education), Shanghai Jiao Tong University, Shanghai 200240, China; 3.Key Laboratory of Smart Manufacturing in Energy Chemical Process of Ministry of Education, East China University of Science & Technology, Shanghai 200237, China)
Abstract:Maintaining population diversity and improving algorithm search efficiency are two major problems that need to be solved urgently in the multimodal multi-objective optimization. To address the above problems, this paper proposed a multimodal multi-objective brain storm optimization algorithm based on zoning search and reinforcement learning(MMBSO-ZSRL) . In the MMBSO-ZSRL, the decision space was first decomposed into multiple subspaces to reduce the search difficulty and maintain the population diversity. Subsequently, the proposed algorithm used SARSA algorithm to balance the global exploration and local exploitation capabilities of the brain storm optimization algorithm. Additionally, the MMBSO-ZSRL utilized the special crowding distance to select individuals for guiding the population evolution. To verify the performance of the proposed algorithm, this paper selected six advanced multimodal multi-objective optimization algorithms and the IEEE CEC2019 multimodal multi-objective problem benchmark test suite for experiments. Experimental results demonstrate that the overall perfor-mance of the MMBSO-ZSRL is significantly better than that of compared algorithms. The proposed MMBSO-ZSRL can not only find the Pareto front with better diversity and approximation, but also find more Pareto optimal solutions in the decision space.
Key words:multimodal multi-objective optimization(MMO); brain storm optimization algorithm; reinforcement learning; SARSA algorithm; zoning search
0 引言
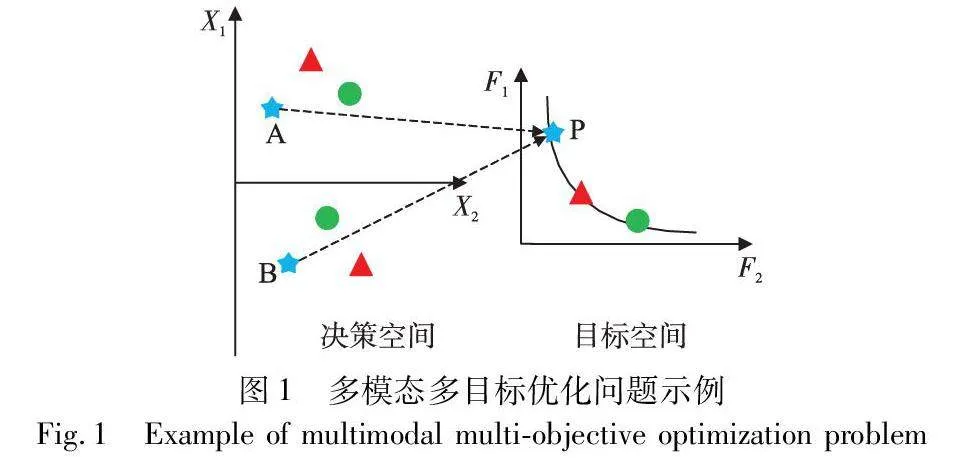
在现实世界中,诸多领域的优化问题都属于多目标优化问题 (multi-objective optimization problems,MOPs)。对于部分MOPs,它们在解空间存在等效帕累托最优解,因此被称为多模态多目标优化问题(multimodal MOPs,MMOPs)[1~3] 。MMOPs广泛存在于各个领域,比如调度优化[4]、火箭发动机设计[5]、多机器人任务分配[6]、配电网故障恢复[7]等。一个典型的多模态多目标优化问题如图1所示。从图1可以看出,决策空间中两个不同点A和B对应相同的目标值P。因此,对于MMOPs而言,在目标空间找到好的帕累托前沿 (Pareto front,PF) 逼近和在决策空间找到足够多的等效帕累托最优解同等重要。此外,由于多模态多目标优化(MMO) 可以提供等效方案,这有助于决策者在不确定/动态环境下找到替代方案,所以受到了广泛关注[2, 3]。
为有效求解MMOPs,诸多学者从环境选择的角度进行研究。比如,Deb等人[8]提出一种综合性的优化算法Omin-optimizer来求解多类优化问题(即单目标、多目标、单模态、多模态优化问题)。不同于之前的研究,该算法通过支配关系、决策空间和目标空间拥挤距离三个指标来对个体进行选择,从而保证解集在决策空间和目标空间的多样性。Yue等人[9]提出一种基于环形拓扑结构和特殊拥挤距离的MMO粒子群算法。该算法使用一种特殊拥挤距离 (special crowding distance,SCD) 来对个体进行选择。此外,还使用一种基于索引的环形拓扑结构来形成稳定的小生境以提高算法的搜索能力。结果表明,所提算法能够有效地提高种群在决策空间的多样性。李文桦等人[10]提出一种同时考虑全局和局部PF的MMO算法。结果表明,与其他算法相比,所提算法能有效兼顾全局和局部帕累托最优解。
为了有效提高决策空间的多样性,研究人员还从搜索空间“隔离”的角度对MMO进行研究。比如,为了保留更多的等效帕累托最优解,Liang等人[11]提出一种基于决策空间小生境方法的MMO算法。结果表明小生境方法可以保留几乎所有的帕累托最优解。随后,Liang等人[12]提出一种基于自组织映射的多目标粒子群算法。该算法首先利用自组织映射策略来建立多个邻域,然后使用精英学习策略提高算法的搜索效率。结果表明,所提算法能在决策空间定位到更多高质量的帕累托最优解。Lin等人[13]提出一种决策和目标空间双聚类的MMO算法。该算法首先在决策空间进行聚类,并选择每个类中的非支配解和目标空间中的高质量解组成临时种群。然后,在目标空间中对该临时种群进行第二次聚类,并在目标空间拥挤的聚类中删除决策空间拥挤的解。结果表明,该算法能有效维持全局和局部帕累托最优解。Hu等人[14]提出一种基于自适应局部搜索的小生境回溯搜索MMO算法。该算法使用亲和力传播算法形成多个小生境,然后在每个小生境中使用所提算子进行搜索。此外,该算法还提出一种自适应局部搜索策略以平衡算法的探索和开发能力。结果表明,所提算法整体性能优于所有对比算法。为解决决策空间种群多样性差和个体空间分布不平衡的问题,Zhang等人[15]提出了一种基于两阶段双小生境的进化策略。该算法分两个阶段解决MMOPs,第一阶段使用决策空间小生境策略,其目标是在决策空间找到具有较好多样性和收敛性的解集;为有效提高决策和目标空间中解集的质量,第二阶段在两个空间同时使用小生境策略。此外,为改善决策空间种群不平衡的问题,设计了一种决策空间密度自适应的策略。结果表明所提算法能够有效求解MMOPs。上述研究大多采用小生境等“软隔离”方法来提高决策空间的多样性。不同于上述方法,Fan等人[16]提出一种“硬隔离”的分区搜索 (zoning search,ZS) 方法以降低MMOPs的求解复杂度。随后,Fan等人[17]又提出一种自适应资源配置的ZS方法来进一步提高搜索效率。Ji等人[18]提出一种基于分区搜索和迁移学习的MMO算法。该算法引入迁移学习方法来实现子空间之间的知识共享。此外,Fan等人[19]提出了一种基于分区搜索的多模态多目标头脑风暴算法。该算法同时使用“软隔离”和“硬隔离”的方法来提高决策空间多样性。结果表明,所提算法在决策和目标空间上都极具竞争力。
在决策空间找到尽可能多的等效帕累托解和在目标空间找到一条高质量的帕累托前沿逼近是MMO的两个重要目标。为进一步提高多模态多目标进化算法(multimodal multi-objective evolutionary algorithm,MMOEA) 的求解性能,本文提出一种基于分区搜索和强化学习的多模态多目标头脑风暴优化算法(multimodal multi-objective brain storm optimization algorithm based on zoning search and reinforcement learning,MMBSO-ZSRL)。在MMBSO-ZSRL中,首先使用分区搜索策略[16]将决策空间分为多个子空间以降低搜索难度,然后使用SARSA算法[20]来自动调整不同搜索算子的选择概率,从而达到提高算法搜索性能的目的,此外,所提算法还利用特殊拥挤距离[9]来选择个体,并将它们来引导种群进化。为了验证MMBSO-ZSRL的性能,本文选取IEEE CEC2019 MMOPs基准测试集[21]与六种先进的MMOEAs[12,16,22~25]进行比较与测试。实验结果显示,MMBSO-ZSRL在PSP[9]和HV[26]两个性能指标上均显著优于其他六种先进的MMOEAs。因此,MMBSO-ZSRL能够搜索到更多的等效帕累托最优解和获得质量更高的PF逼近。
1 预备知识
1.1 多目标优化问题
多目标优化问题(以最小化问题为例)定义如下[27]:
min F(x)=(f1(x),f2(x),…,fM(x))s.t. x∈Ω(1)
其中:M表示目标的数量;x=(x1,x2,…,xD)为D维决策向量;Ω表示决策空间。其他一些相关概念描述如下[27]:
定理1 帕累托支配关系。向量q=(q1,q2,q3,…,qM)支配另一个向量q=(q1,q2,q3,…,qM)(记作pq)的条件是:i∈{1,2,3,…,M},pi≤qi∧j∈{1,2,3,…,M},pj<qj。
定理2 帕累托最优解集(Pareto optimal set,PS)。一个向量x*∈Ω,若不存在其他向量x∈Ω,使得F(x)F(x*),就称x*为帕累托最优解。所有的帕累托最优解构成的集合(记作X*),称为PS。
定理3 帕累托前沿(Pareto front,PF)。在多目标优化问题中,PF={F(x*)|x*∈X*}。
1.2 多模态多目标优化问题及评价指标
相比于1.1节的多目标优化问题,MMOPs是其一种特殊类型。若一个多目标优化问题满足以下任一条件[9,11],则该问题属于MMOPs:a)问题至少有一个局部帕累托最优解集;b)问题存在至少两个等效全局帕累托最优解集对应于同一PF。MMO既要在目标空间找到高质量的PF逼近,又要保证找到决策空间足够多的等效帕累托最优解。因此,本文使用帕累托解集近似(Pareto set proximity,PSP)[9]和超体积值(hypervolume,HV)[26]这两个性能指标来评价MMOEAs的性能。具体定义如下:
1)PSP
PSP用于评估所得解集PS*与真实帕累托最优解集PS的相似性,其计算公式如式(2)所示。PSP值越大,表示算法在决策空间中的表现越好。
PSP=CRIGDx
IGDx(PS,PS*)=∑v∈PS*d(v,PS)|PS*|
CR=(∏Dj=1δj)12D
δj=1 Vmaxj=Vminj
0vminj≥Vmaxj‖vmaxj≤Vminj
min(vmaxj,Vminj)-max(vminj,Vmaxj)Vmaxj-Vminjotherwise(2)
其中:CR为覆盖率;IGDx是决策空间反世代距离[28];d(v,PS)指v与PS中最近点的欧氏距离;|PS*|表示PS*中解的数量;vmaxj和vminj分别表示PS中第j个维度的最大值和最小值;Vmaxj和Vminj分别表示PS*中第j个维度的最大值和最小值;max和min分别表示最大值函数和最小值函数。
2)HV
HV反映所获得PF逼近的收敛性和多样性,其计算公式如式(3)所示。HV值越大,代表算法所获得PF逼近越接近真实PF,算法在目标空间中的表现越好。
HV(PS)=VOL(∪x∈PS*[f1(x),r1]×…×[fM(x),rM])(3)
其中:VOL为勒贝格测度;r* = (r*1,r*2,…,r*M)是选择的参考点。
1.3 头脑风暴优化算法
受人类头脑风暴过程的启发,Shi等人[29]于2011年提出一种模拟人类集体行为的头脑风暴优化(brain storm optimization,BSO)算法。BSO算法的步骤[29~31]如下:
a)随机生成一个初始种群。
b)使用K-means聚类方法将种群分为K个聚类,对每个聚类中的个体进行排序,并将好的个体作为该类的聚类中心。
c)以一定概率Pre产生随机个体替代某一类的聚类中心。
d)在任意一个聚类中,选择一个随机个体或者聚类中心来产生候选个体xtselect;或者在任意两个聚类中,分别选择它们的随机个体或者聚类中心来生成xtselect。产生xtselect的具体方式如下[29]:
if p1<0.8
xtselect=xc if p2<0.4xrotherwise(4)
else
xtselect=w1×xc1+(1-w1)×xc2 if p3<0.5w1×xr1+(1-w1)×xr2otherwise(5)
end
其中:xc和xr分别为任意一个聚类的聚类中心和随机个体;xc1和xc2为任意两个聚类的聚类中心;xr1和xr2为任意两个聚类的随机个体;p1、p2、p3和w1都为[0,1]的随机数。
然后,通过高斯变异来产生新个体xtnew,公式如下:
xtnew=xtselect+ξ(t)×N(μ,σ)
ξ(t)=log sig0.5×T-tz×rand(6)
其中:ξ为变异系数;N(μ,σ)是均值为μ,方差为σ的高斯随机数;logsig为对数S型传递函数;T表示最大迭代次数;z是改变logsig函数的斜率;rand为[0,1]的随机数。
e)选择较好的个体进入下一次的迭代。
f)如果生成的新个体数没有达到N,则返回步骤d)。
g)若达到最大迭代次数,则输出最终解;否则返回步骤b)。
2 基于分区搜索和强化学习的多模态多目标头脑风暴优化算法
如何得到更多高质量的等效帕累托最优解一直是求解MMO的难点。BSO算法在求解多模态优化问题方面有较好表现[30]。基于此,为有效解决MMOPs,本文提出一种MMBSO-ZSRL算法。
2.1 分区搜索
由于MMOPs的解集在决策空间有多模态特性,所以大的搜索空间会对算法搜索带来极大困难。根据文献[16,32],使用分区策略不仅可以缩小算法的搜索空间,而且能以“物理隔离”的方式提高/维持种群的多样性;从而辅助MMOEAs找到更多等效Pareto解。为此,本文同样使用分区搜索策略来对整个搜索空间进行划分,以此来降低各个子区域的搜索难度。具体步骤如下,随机选择h(1≤h≤D)个决策变量,然后将每个决策变量等分成e段。因此,搜索空间被划分为w=eh个子空间。
2.2 基于特殊拥挤距离的个体选择方法
文献[9]提出一种特殊拥挤距离(special crowding distance,SCD) 来对种群个体进行评价,其计算公式如下[9]:
SCDi=max(CDi,x,CDi,f) if CDi,x>CDavg,x or
CDi,f>CDavg,f
min(CDi,x,CDi,f)otherwise(7)
其中:CDi,x和CDi,f分别表示第i个个体在决策和目标空间中的拥挤距离;CDavg,x和CDavg,f分别表示决策和目标空间中所有个体拥挤距离的平均值。由于利用SCD能够挑选出高质量的个体,所以使用它来引导种群进化。根据文献[9],使用式(7) 得到每个个体的SCD值,然后使用概率公式来计算子种群中各个个体被选中的概率。概率公式计算如下:
pri=SCDi∑ni=1SCDi(8)
其中:n为该子种群的种群规模。所提个体选择方法分为三个步骤:a) 根据式(8)计算出子种群中所有个体所对应的概率值;b) 根据概率值计算子种群中各个个体被选中的概率区间;c) 产生一个随机数rand,当rand落在某区间内,则该区间的个体被选中。
2.3 改进的BSO算法生成策略
2.3.1 个体生成公式的改进
尽管BSO算法在多模态优化中具有良好的性能,但固定的搜索模式可能难以适应不同的进化阶段。因此,本文提出了一种改进的个体生成策略。
if p1<P1
xtnew=xcpr+F×(xnbest-xcpr)+F×(xr1-xr2) p2<P2
xrpr+ξ(t)×N(μ,σ1)otherwise(9)
else
xtnew=w1×xc1+(1-w1)×xc2+ξ(t)×N(μ,σ) p3<P3
w1×xr1+(1-w1)×xr2+ξ(t)×N(μ,σ)otherwise(10)
end
其中:F是缩放因子;xcpr是使用2.2节所提方法得到的聚类中心;xnbest是该聚类中不同于xcpr的非支配个体;xrpr是使用2.2节所提方法得到的普通个体;σ1为小于方差σ的参数值;P1、P2、P3为概率参数,取值为[0,1]。
2.3.2 生成策略自适应
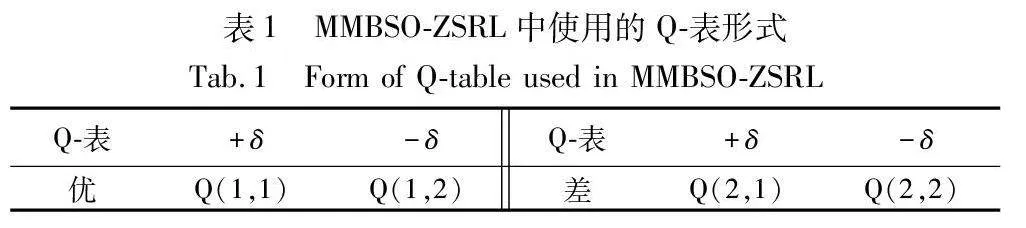
在BSO算法搜索过程中,不同的搜索算子对其性能有显著影响。为使BSO算法能够根据进化过程实现自主调整,本文利用SARSA(state-action-reward-state-action)算法[20]来达到以上目的。为了评价不同搜索算子的性能,首先根据不同的个体生成策略将种群划分为四个子种群,然后使用式(2)计算四个子种群的PSP值。动作空间定义为AC=[+δ,-δ];状态空间定义为SV=[优,差];奖励设置为RC=[1,-1]。针对P1、P2、P3三个参数,分别建立Q-1表、Q-2表、Q-3表。Q-表的形式,见表1。
在MMBSO-ZSRL算法中,更新动作链AC的步骤如下:
a)由策略xcpr+F×(xnbest-xcpr)+F×(xr1-xr2)和xrpr+ξ(t)×N(μ,σ1)生成个体的子种群分别表示为OP1和OP2;由策略w1×xc1+(1-w1)×xc2+ξ(t)×N(μ,σ)和w1×xr1+(1-w1)×xr2+ξ(t)×N(μ,σ)生成个体的子种群分别表示为OP3和OP4。
b)性能评估。使用式(2)分别计算OP1、OP2、OP3和OP4的PSP值,表示为PSP1、PSP2、PSP3和PSP4。对于P1值,若 (PSP1+PSP2)>(PSP3+PSP4),那么P1的奖励值为1;反之,P1的奖励值为-1。对于P2,若PSP1>PSP2,那么P2的奖励值为1;反之,P2的奖励值为-1。对于P3,若PSP3>PSP4,那么P3的奖励值为1;反之,P3的奖励值为-1。
c)根据步骤b)判断P1、P2、P3所对应的状态s′和奖励值r,更新对应的状态向量SV和奖赏链RC。
d)在对应的状态s′下,使用贪心策略[20]预测相应的动作a′。
e)根据式(11)[20]更新对应P1、P2、P3的Q-表。
Q(s,a)=Q(s,a)+α(r+γQ(s′,a′)-Q(s,a))(11)
f)更新对应的动作链AC。
2.4 MMBSO-ZSRL算法框架
所提算法MMBSO-ZSRL的伪代码见算法1。第1行,首先使用分区搜索策略将整个决策空间分为w个子空间。第3行,初始化当前迭代次数、P1、P2、P3及它们的Q-表、状态向量、动作链、奖赏链。第4行,在第i个子空间中,随机初始化种群POPi(0)、初始化聚类中心存档CAi。第6行,在决策空间使用K-means算法将种群POPi(t)分成K个聚类。第7~10行,对K个聚类分别使用non-dominated_scd_sort方法[9]进行排序。此外,在每个聚类中随机选择一个非支配个体保存至CAi。第12~14行,以一定的概率产生随机个体取代某一类的聚类中心,以避免算法陷入局部最优[29]。第16~20行,使用2.3.1节改进的BSO个体生成策略产生N个新个体并保存。第21行,通过2.3.2节所提的生成策略自适应方法更新概率参数。第22行,种群POPi(t+1)与POPi(t)合并,并使用non-dominated_scd_sort方法[9]进行排序,取其前N个个体存入POPi(t+1)进行下一次的迭代。第25行,达到第i个子空间的最大迭代次数后,保存该子空间内最后一次迭代种群POPi(T/w)中的非支配个体。第27、28行,将所有子空间中的非支配个体合并,使用多目标处理技术[27] (记为selection) 得到最终的PS和PF。
算法1 MMBSO-ZSRL算法
输入:子空间数w;最大迭代次数T;种群规模N;聚类数K。
输出:PS和PF。
1 根据2.1节对搜索空间分区得到w个子空间,记作S1,S2,…,Sw;
2 for i=1:w do
3 初始化当前迭代次数t=0、概率参数P1、P2、P3及它们的Q-表、状态向量SV、动作链AC、奖赏链RC;
4 初始化种群POPi(0)和聚类中心存档CAi;
5 while t<T/w do
6 在搜索空间使用K-means算法将种群POPi(t)分成K个聚类,分别记作C1,C2,…,CK;
7 for k=1:K do
8 使用non-dominated_scd_sort方法对聚类Ck进行排序;
9 在Ck中,随机选择一个非支配个体,存档在CAi中;
10 end for
11 //以一定概率产生随机个体取代某一类的聚类中心
12 if rand<0.2 then
13 在CAi中,用一个随机个体替换掉随机选中的一个聚类中心;
14 end if
15 //产生N个新个体
16 for k=1:K do
17 for l=1:|Ck| do
18 使用2.3.1节所提策略产生新个体并保存至POPi(t+1);
19 end for
20 end for
21 通过2.3.2节所提的生成策略自适应方法更新概率参数;
22 通过non-dominated_scd_sort方法对POPi(t+1)和POPi(t)排序,取其前N个个体存入POPi(t+1); //环境选择
23 t=t+1; //更新迭代次数
24 end while
25 保存POPi(T/w)中的非支配个体,得到PSi和PFi;
26 end for
27 PS=selection(PS1∪PS2∪…∪PSw);
28 PF=selection(PF1∪PF2∪…∪PFw).
2.5 所提算法复杂度分析
本节讨论所提MMBSO-ZSRL在最坏情况下的运行时间复杂度。各个子空间内主要执行以下步骤:聚类、选择聚类中心、新个体生成、环境选择。在本文中,种群规模、问题的目标数量、决策变量维度分别为N、M、D。对每一代使用K-means算法聚类的时间复杂度为O(t1KND),其中,t1为K-means算法的迭代次数。选择聚类中心的时间复杂度为O(KM|Ck|2)。对于新个体的生成,时间复杂度为O(K|Ck|2)。此外,对于环境选择,其计算复杂度为max{O(M(2N)2,O(M(2N) log(2N)),O(D(2N) log(2N))}。MMBSO-ZSRL的最终时间复杂度为max{O(t1TKND),O(TKM|Ck|2),O(TM(2N)2),O(TD(2N) log (2N) },T为迭代次数。在本文中,t1≈5;K=15;M=D=2 or 3;|Ck|≈N/K。因此,N>|Ck|>K>t1>M=D。故可以确定MMBSO-ZSRL的运行时间复杂度为O(TM(2N)2)。
3 实验结果
为验证所提算法的性能,将MMBSO-ZSRL与其他六种知名的多模态多目标优化算法进行比较。它们分别是SMPSO_MM[12]、SS_MOPSO[24]、MMODE_CSCD[23]、MMODE_ICD[22]、MMOHEA[25]和ZS-MO_Ring_PSO_SCD[16]等。同时,IEEE CEC2019 MMOPs测试函数集[21]被用来测试它们的性能;并利用PSP和HV来评估所有比较算法的性能。另外,为保证实验结果分析的可靠性,采用Wilcoxon[33]秩和检验和Friedman[34]检验来对实验结果进行统计分析,显著性水平设置为5%,其中“+”和“-”分别表示MMBSO-ZSRL优于和劣于相比较算法,“=”表示MMBSO-ZSRL与相比较的算法性能接近。
3.1 实验设置
对于所有比较算法,它们的种群规模和最大适应度函数评估次数分别设置为800和80 000。另外,在MMBSO-ZSRL中,K设为15,δ设为2.5%,σ1设为0.2,w设为4。对于其他对比算法,它们的参数设置与原始文献[12,16,22~25]的设置一致。此外,所有比较算法都使用MATLAB R2021a实现,并在每个测试函数上独立运行21次。
3.2 实验结果
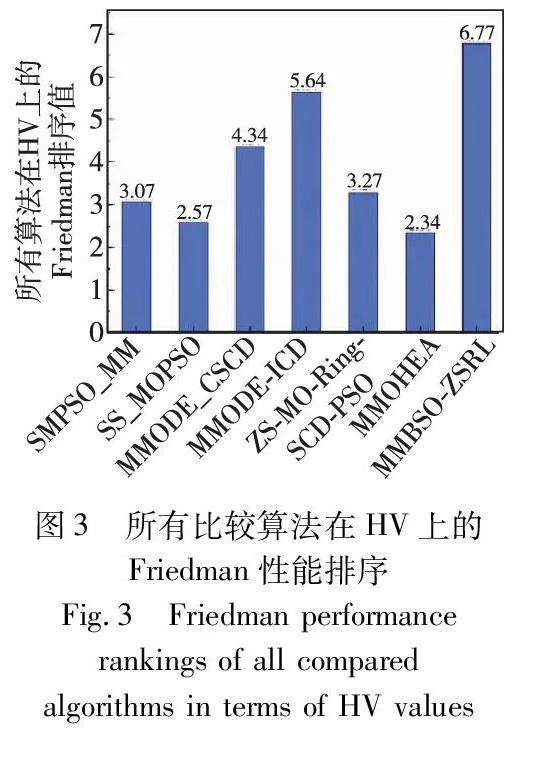
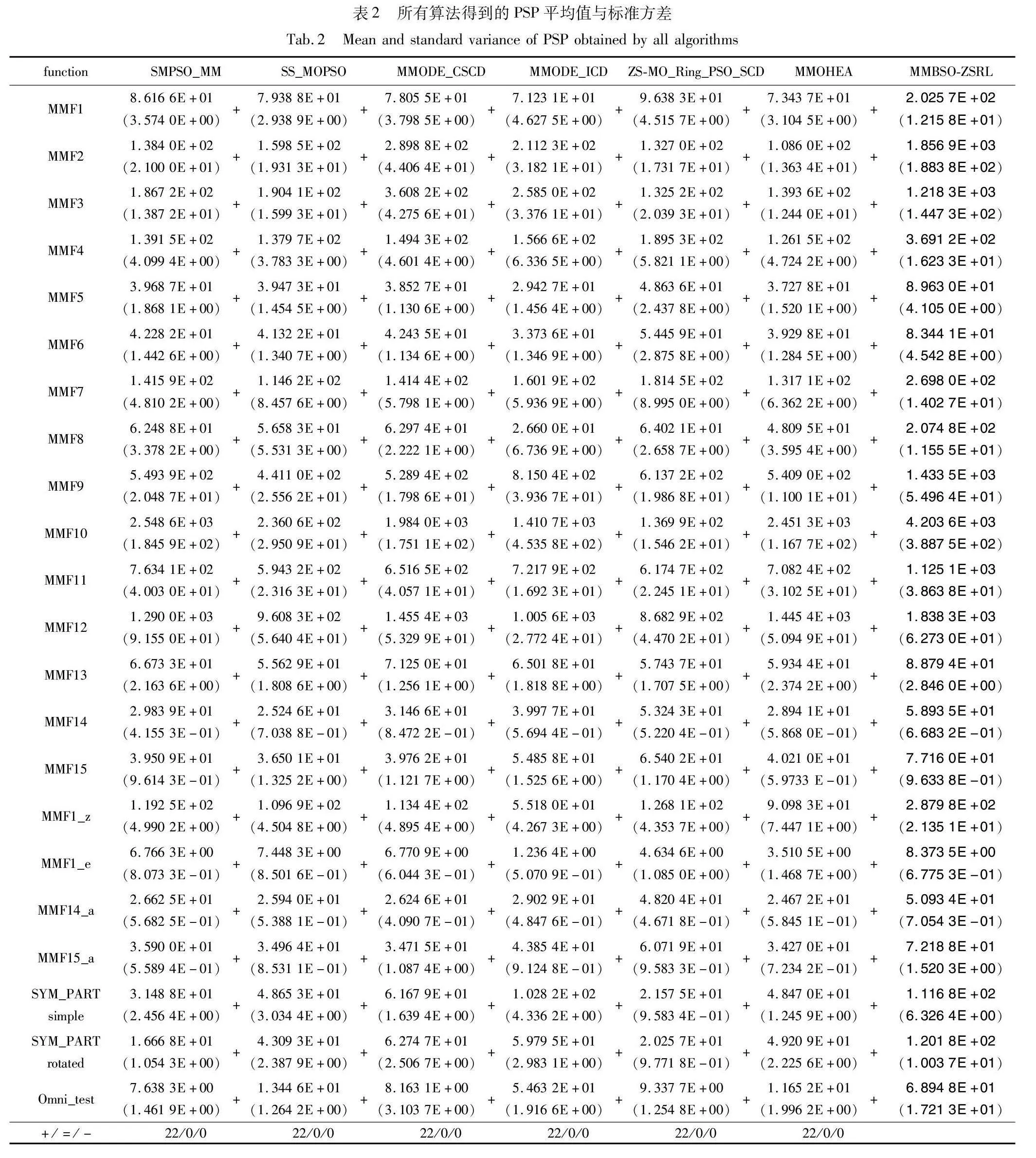
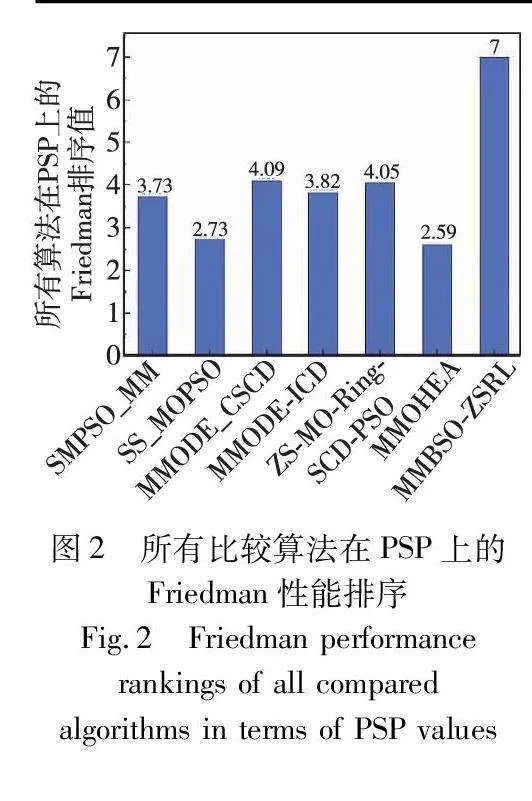
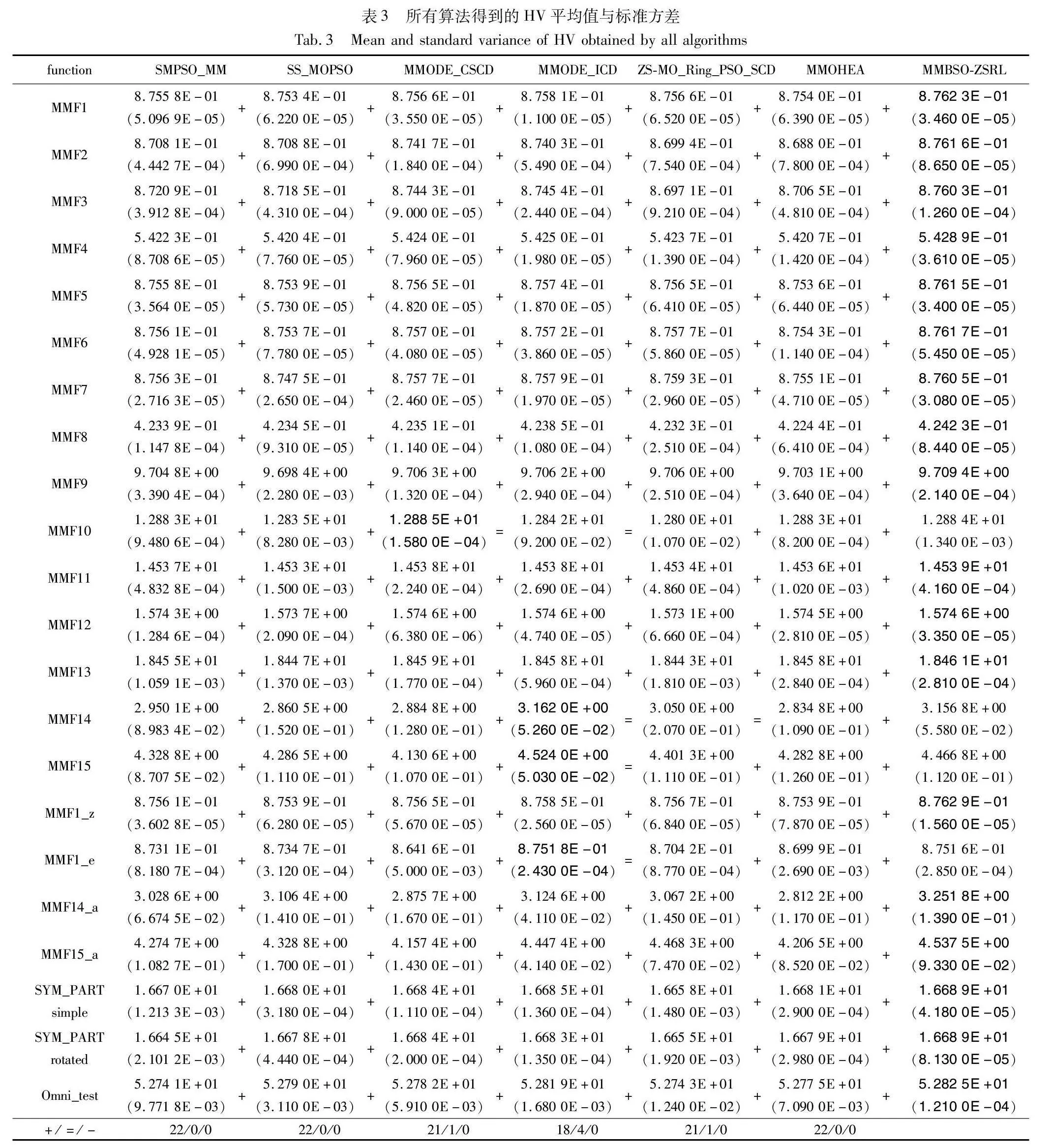
所有比较算法的PSP和HV的平均值和标准方差如表2、3所示。为有效区分各个比较算法与所提算法的性能,本文采用Wilcoxon秩和检验来对它们的结果进行统计分析。统计分析结果也显示在表2、3。此外,表中最好的结果用粗体表示。从表2可以看出,对于PSP性能指标,MMBSO-ZSRL在22个测试函数上的表现要显著好于其他六种多模态多目标进化算法。这表明所提算法能够在决策空间中找到更多的等效帕累托最优解。主要原因是所提算法使用分区搜索策略来降低各个子区域的搜索难度和有效维持种群多样性。同时,MMBSO-ZSRL分别使用改进的BSO生成策略来提高算法的搜索能力和利用SCD来挑选高质量的个体来引导种群进化。因此,相比于其他比较算法,所提算法不仅具有较强的全局探索能力,而且还拥有很好的局部开发能力;这有助于它在决策空间找到更多的帕累托最优解。除了以上结果,本文还使用Friedman检验来对所有比较算法的性能进行排序,其排序结果如图2所示。从图2可以看出,MMBSO-ZSRL在PSP性能指标上的综合表现是最好的。因此,所提算法是一种求解MMOPs的有效方法。从表3可以观察到,对于HV性能指标,MMBSO-ZSRL在IEEE CEC 2019 MMOPs测试函数集上总体表现出比其他算法更好的性能。具体来说,22个测试问题中,MMBSO-ZSRL在18个问题上表现出了最佳性能。主要原因可能是:MMBSO-ZSRL综合了“软隔离”(K-means聚类)和“硬隔离”(分区搜索)的优势,找到了更多的帕累托最优解,从而提高解集在目标空间中的多样性。此外,MMODE_CSCD、MMODE_ICD、ZS-MO_Ring_PSO_SCD分别在1个、4个、1个测试问题上获得了相似性能的HV值。主要原因可能是:对于MMOPs来讲,只要得到部分PS,也能获得收敛性和多样性好的PF逼近。这也是其他六种比较算法与所提算法在PSP指标上差距很大,却在HV指标上差距并不大的原因。此外,从图3还可以看出,MMBSO-ZSRL在HV指标上的Friedman性能排序是最好的。因此,所提算法能够在目标空间中得到好的PF逼近。
综上所述,MMBSO-ZSRL在决策空间和目标空间中的表现是所有比较算法中最好的。所提算法不仅可以在目标空间中找到逼近性和多样性好的PF逼近,而且能够定位到更多的等效帕累托最优解。
4 实验分析
4.1 分区搜索策略对MMBSO-ZSRL算法的影响
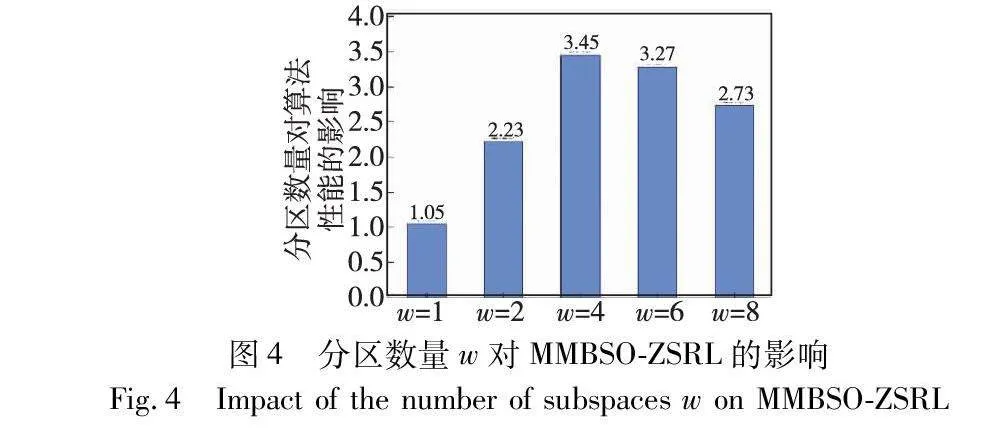
为验证分区搜索策略的有效性,本文选用没有使用分区搜索策略(即w=1)的MMBSO-ZSRL(命名为MMBSO-v1)作为对照组,将子空间数量w分别设为1,2,4,6,8进行实验。对算法在22个测试函数上运行21次所得到的PSP平均值进行Fridman性能排序,所得结果见图4。从图4可以看出,随着子空间数量的增加,算法性能呈现先上升后下降的趋势。这主要是当总的计算资源固定时,各个分区的计算资源会随着分区数量的增加而减少。当分区数量和各个分区的资源达到平衡状态时,这个时候分区数量可以使得算法性能达到最佳。但当分区数量继续增加,每个搜索子空间的计算资源会变少,因此整体性能会下降。此外,从图4可以看出,当w=4时,所提算法获得最佳性能。因此,在所提算法中,分区数量设定为4。
4.2 基于SCD的个体选择方法对算法的影响
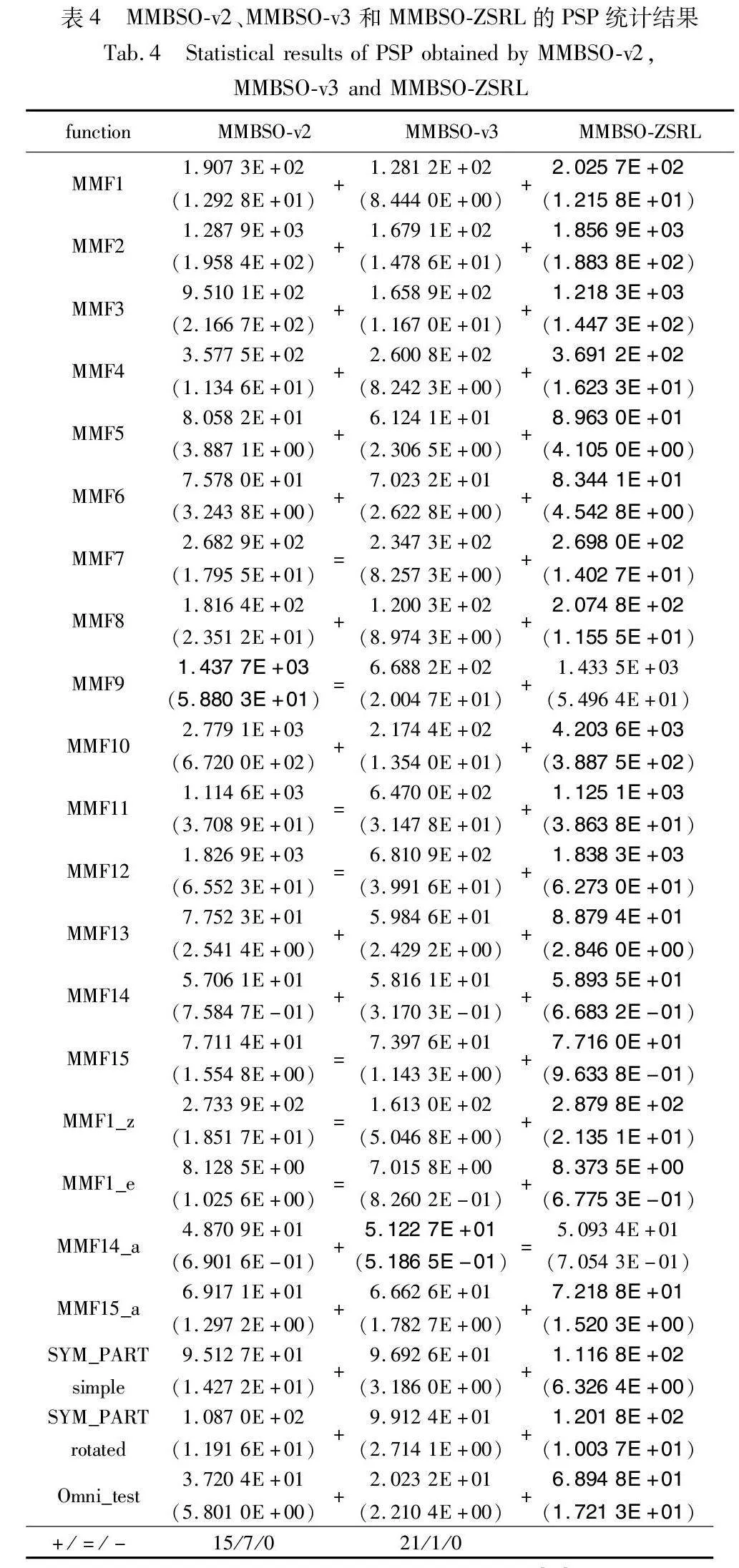
为验证基于SCD的个体选择方法的有效性,本文选择没有采用该方法的MMBSO-ZSRL(命名为MMBSO-v2)和MMBSO-ZSRL进行性能比较。两个算法的所得结果如表4所示。最佳结果用粗体表示。
为确保结论的可靠性,本文使用Wilcoxon[33]秩和检验来对结果进行统计分析,相应的统计结果见表4。从表4可以看出,MMBSO-ZSRL在15个测试函数上得到的PSP值明显优于MMBSO-v2,且在其余7个测试问题上与MMBSO-v2取得了相似的结果。相比于MMBSO-v2,MMBSO-ZSRL算法在在求解复杂优化问题(例如SYM_PART rotated、Omni_test等)时,具有更好表现。因此,在大多数测试问题上,基于SCD的个体选择方法可以依据决策空间和目标空间的拥挤信息挑选高质量个体引导种群进化,从而辅助MMBSO-ZSRL找到更多的等效帕累托最优解。
4.3 改进的BSO算法生成策略的效果
本文采用未应用改进BSO算法生成策略的MMBSO-ZSRL(命名为MMBSO-v3)和MMBSO-ZSRL进行性能比较,以验证所改进BSO算法生成策略的有效性。MMBSO-v3和MMBSO-ZSRL在22个测试函数上各运行21次,所得PSP值的平均值和标准方差显示在表4中。为确保结论的可靠性,本文还使用Wilcoxon[33]秩和检验来统计分析结果,相应的统计结果也列于表4中。此外,最佳结果用粗体表示。从表4可以看出,MMBSO-ZSRL在21个测试函数上所得到的PSP值都明显优于MMBSO-v3;仅在测试函数MMF14_a上,两个算法取得了相似的结果。这表明所改进的BSO生成策略可以在绝大多数测试问题上有效提高MMBSO-ZSRL的搜索效率,从而找到更多的等效帕累托最优解。
为进一步验证所提生成策略自适应方法的有效性,使用MMF3测试函数来对P1、P2、P3进行分析。它们在各个分区的变化趋势见图5。较小的P1值有助于全局搜索;而较大的P1值会偏向算法进行局部搜索。从图5可以发现,P1值在4个子空间都呈上升趋势。因此,在进化后期,所提算法能以较高的概率选择式(9) 来对各个子空间进行局部精细搜索,这有助于得到更高质量的解集。同时,从图5可以看出,P2值在整个搜索过程中呈变大趋势,这表明xcpr+F×(xnbest-xcpr)+F×(xr1-xr2)能够为所提算法找到更好的Pareto解。另外,从图5(a)(c)来看,P3值随进化过程而变大,这说明在子空间1和3中,全局搜索能力较强的搜索策略占据主导地位。这可以有效帮助所提算法提高搜索性能。而从图5(b)(d)可以看出,两种搜索策略在其子空间中的作用几乎相当。因此,本文可以看出,所提自适应方法可以根据实际情况来自动调整算法的搜索性能以找到更多和更高质量的Pareto解。
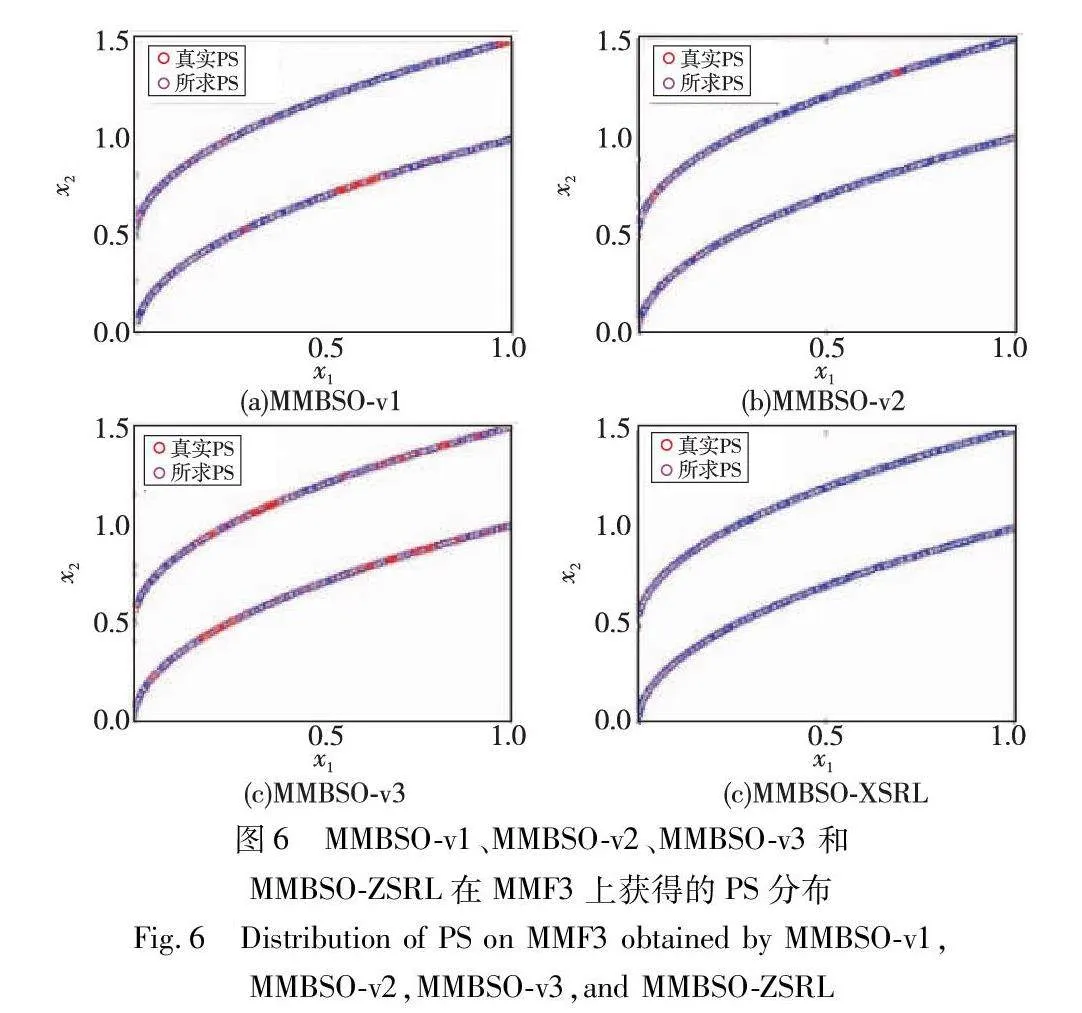
4.4 视觉效果
为更直观体现所用方法的效果,使用MMBSO-v1、MMBSO-v2、MMBSO-v3和MMBSO-ZSRL来对MMF3问题进行测试。所有算法的PSs如图6所示。
从图6 (a)可以看出,由于未使用分区策略,所以MMBSO-v1算法得到解集在均匀性方面要逊于MMBSO-ZSRL。同样,SCD的个体选择方法和BSO生成策略同样对所提算法的性能产生影响。因此,改进方法对所提算法的性能提升都起到了很大帮助。
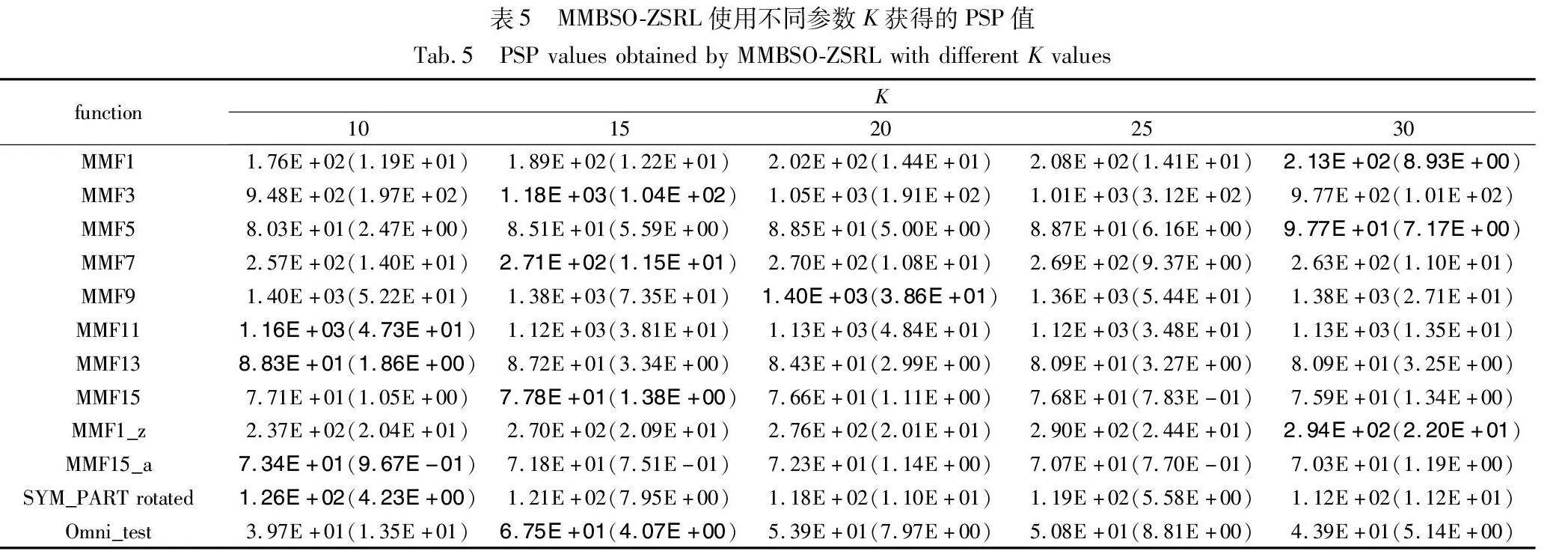
4.5 参数K的敏感性分析
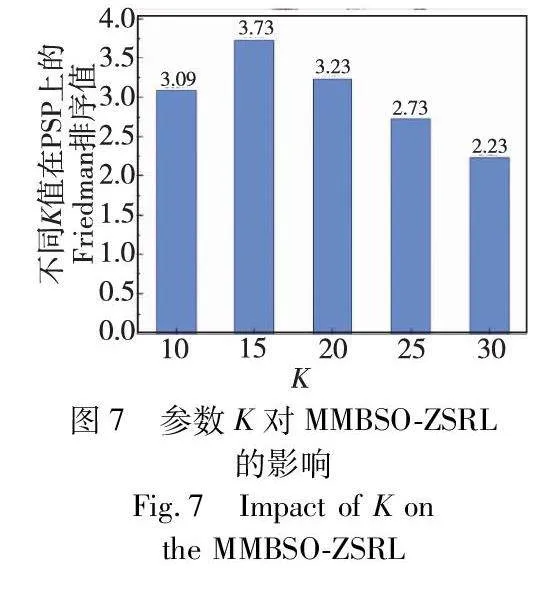
聚类数K对MMBSO-ZSRL的性能可能有较大影响,故本实验对参数K进行敏感性分析。一般来说,虽然大的K值能提高种群的多样性,但是会影响种群的收敛速度。相反,如果K值太小,种群的多样性可能无法得到有效维持。为了验证MMBSO-ZSRL在不同K值下的性能,使用控制变量法进行实验分析。当参数δ设为1.0%,参数σ1设为0.2,将K值分别设置为10、15、20、25、30进行实验。结果如表5所示,最佳结果用粗体标出。从表5可以看出,没有任何一个K值使得MMBSO-ZSRL在所有问题上都能取得最好结果。因此,使用Friedman检验[34]对实验结果进行分析,得到的性能排序结果见图7。如图7所示,随着聚类数K值的增加,算法的整体性能先上升,后下降。其中,当K值取15时,MMBSO-ZSRL获得最佳整体表现。因此,在MMBSO-ZSRL中,将K值设为15。
4.6 参数δ的敏感性分析
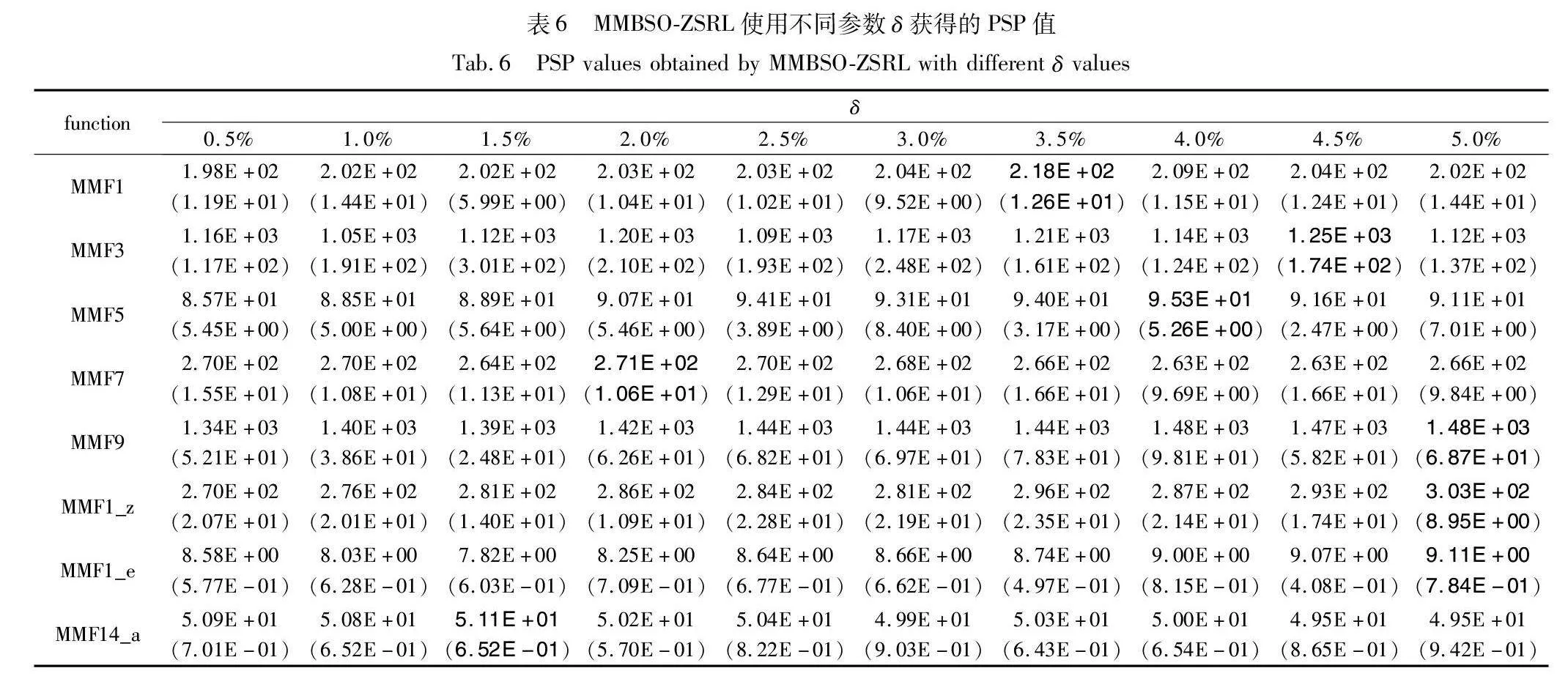
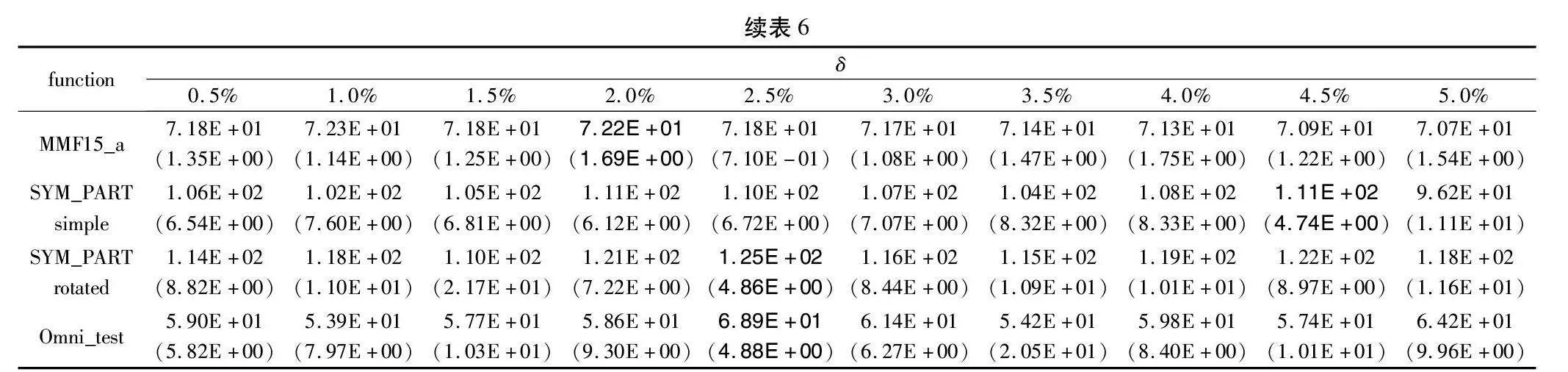
控制参数δ可能会对MMBSO-ZSRL的性能产生一定影响。为验证MMBSO-ZSRL在不同δ值下的表现,对其实验分析。本文使用控制变量法,当参数K设为15、参数σ1设为0.2,将δ值分别设置为0.5%、1.0%、1.5%、2.0%、2.5%、3.0%、3.5%、4.0%、4.5%、5.0%进行实验。实验结果见表6,最佳结果用粗体标出。
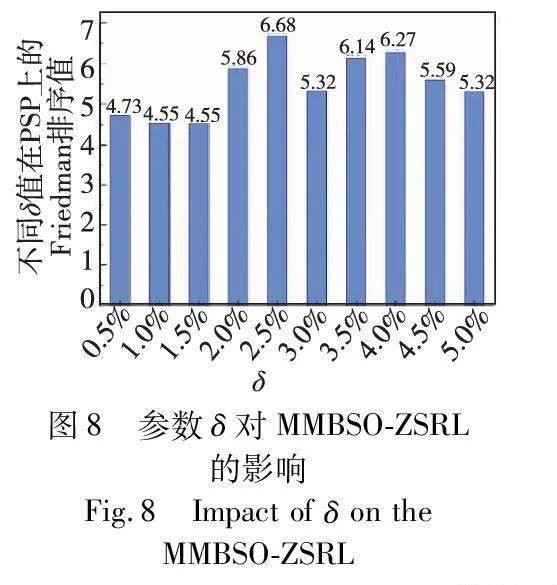
从表6可以看出,不同δ值都只能在少数测试问题上取得最好结果。即,在一定范围内,不同δ值对MMBSO-ZSRL的性能影响是有限的。为使MMBSO-ZSRL获得最佳性能,本文使用Friedman检验[34]对实验结果进行进一步性能排序;排序结果如图8所示。可以看出,在δ值取2.5%的时候,MMBSO ZSRL获得最佳性能。因此,在MMBSO-ZSRL中,将δ值设为2.5%。
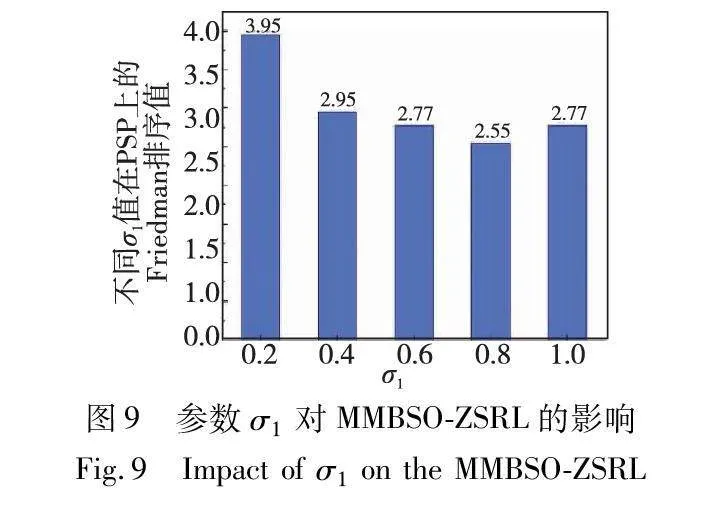
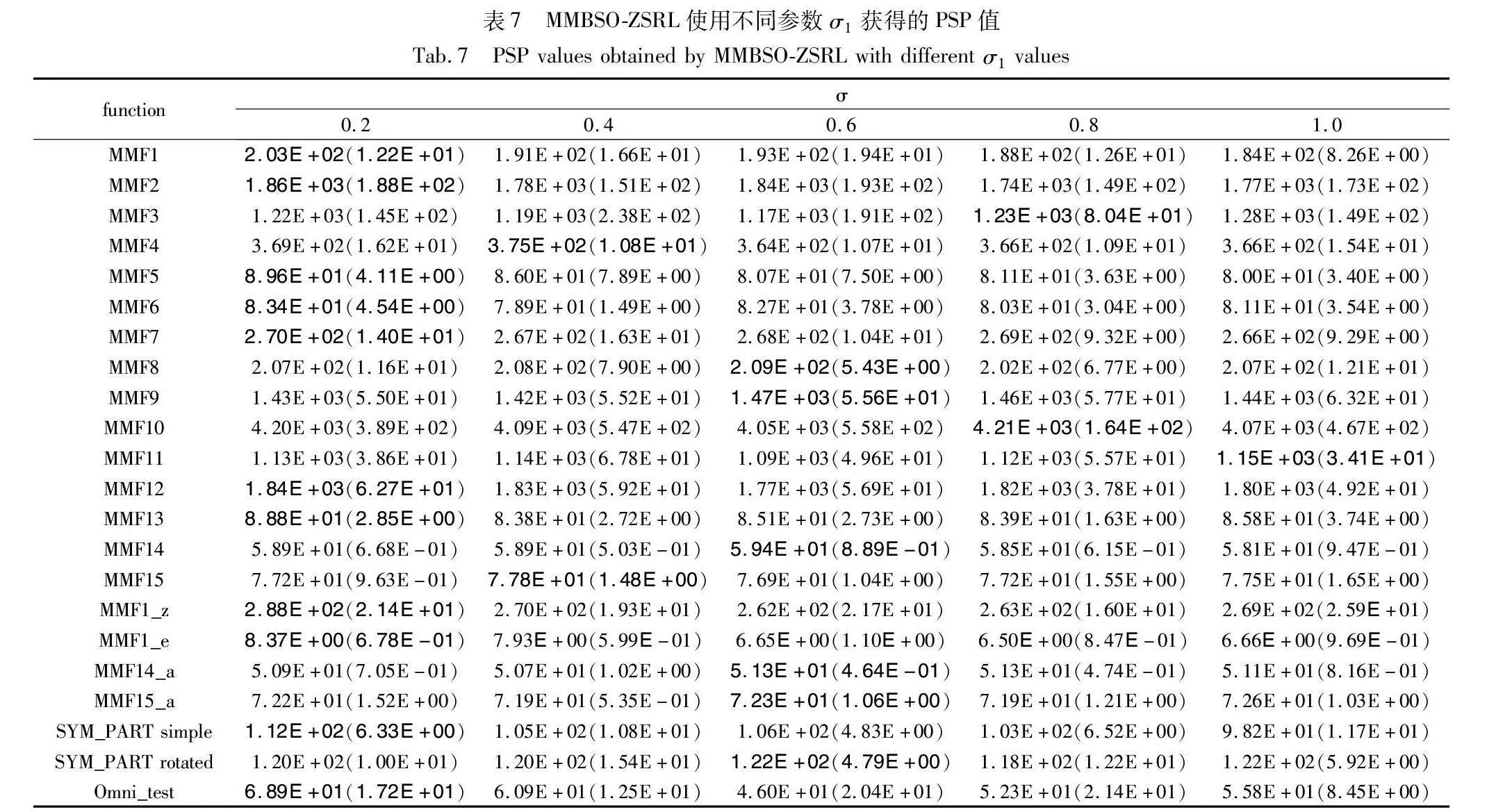
4.7 参数σ1的敏感性分析
为验证MMBSO-ZSRL在不同σ1值下的性能,当参数K设为15、δ设为2.5%时,将参数σ1分别设为0.2、0.4、0.6、0.8、1.0进行实验。实验结果如表7所示,最好结果用粗体标出。从表7可以看出,所有σ1值均未能使MMBSO-ZSRL在全部测试问题上取得最好结果。因此,对实验结果使用Friedman检验[34]进一步分析,所得性能排序结果见图9。如图9所示,随着σ1值取的增加,MMBSO-ZSRL的性能呈下降趋势,且取0.2的时候获得最佳性能。因此,在MMBSO-ZSRL中,将σ1值设为0.2。
5 结束语
为维持种群多样性和提高算法搜索效率以及获得尽可能多的等效帕累托最优解,本文提出了一种基于分区搜索和强化学习的多模态多目标头脑风暴优化算法。在该算法中,首先将决策空间分解为多个子空间以降低搜索难度并提高种群多样性;然后,使用SARSA来平衡头脑风暴优化算法的全局探索和局部开发能力;并使用特殊拥挤距离来挑选个体指导种群进化。为测试所提算法性能,本文选取六种先进的MMOEAs进行对比,并选用IEEE CEC 2019 MMOPs 基准测试集来对所有算法的性能进行测试。此外,在实验分析中设计三组对照实验来验证所提方法的有效性。结果表明,分区搜索可以有效提高种群多样性且降低MMOPs的求解难度;改进BSO生成策略可以有效提高算法的搜索效率;基于特殊拥挤距离的个体选择方法可以有效辅助MMBSO-ZSRL找到更多的帕累托最优解。此外,为检验参数对MMBSO-ZSRL性能的影响,本文设计了三组对照实验来进行参数敏感性分析,实验结果表明,在K取值为15,δ取值为2.5%,σ1取值为0.2时,算法整体性能最佳。综上所述,相比于其他算法,MMBSO-ZSRL能够在决策空间找到更多帕累托最优解,且获得质量更高的PF逼近。未来将对MMBSO-ZSRL做进一步研究,使其能够解决约束多模态多目标优化问题,并探究其在实际工程应用中的性能表现。
参考文献:
[1]Li Wenhua, Zhang Tao, Wang Rui, et al. Multimodal multi-objective optimization: comparative study of the state-of-the-art[J]. Swarm and Evolutionary Computation, 2023, 77: article ID 101253.
[2]Tanabe R, Ishibuchi H. A review of evolutionary multimodal multi-objective optimization[J]. IEEE Trans on Evolutionary Computation, 2020,24(1): 193-200.
[3]岳彩通, 梁静, 瞿博阳, 等. 多模态多目标优化综述[J]. 控制与决策, 2021,36(11): 2577-2588. (Yue Caitong, Liang Jing, Qu Boyang, et al. A review of multimodal multiobjective optimization[J]. Journal of Control and Decision, 2021, 36(11): 2577-2588.)
[4]Pérez E, Posada M, Herrera F. Analysis of new niching genetic algorithms for finding multiple solutions in the job shop scheduling[J]. Journal of Intelligent Manufacturing, 2012, 23(3): 341-356.
[5]Kudo F, Yoshikawa T, Furuhashi T. A study on analysis of design variables in pareto solutions for conceptual design optimization problem of hybrid rocket engine[C]//Proc of IEEE Congress of Evolutionary Computation. Piscataway, NJ: IEEE Press, 2011: 2558-2562.
[6]Miao Zhenhua, Huang Wentao, Jiang Qingchao, et al. A novel multimodal multi-objective optimization algorithm for multi-robot task allocation[J/OL]. Trans of the Institute of Measurement and Control.(2023-06-25).https://doi.org/10.1177/01423312231183588.
[7]Li Xin, Li Mingyang, Yu Moduo, et al. Fault reconfiguration in distribution networks based on improved discrete multimodal multi-objective particle swarm optimization algorithm[J]. Biomimetics, 2023, 8(5): article ID 431.
[8]Deb K, Tiwari S. Omni-optimizer: a generic evolutionary algorithm for single and multi-objective optimization[J]. European Journal of Operational Research, 2008, 185(3): 1062-1087.
[9]Yue Caitong, Qu Boyang, Liang Jing. A multiobjective particle swarm optimizer using ring topology for solving multimodal multiobjective problems[J]. IEEE Trans on Evolutionary Computation, 2017, 22(5): 805-817.
[10]李文桦, 明梦君, 张涛, 等. 考虑全局和局部帕累托前沿的多模态多目标优化算法[J]. 自动化学报, 2023, 49(1): 148-160. (Li Wenhua, Ming Mengjun, Zhang Tao, et al. Multimodal multi-objective evolutionary algorithm considering global and local Pareto fronts[J]. Acta Automatica Sinica, 2023, 49(1): 148-160.)
[11]Liang Jing, Yue Caitong, Qu Boyang. Multimodal multi-objective optimization: a preliminary study[C]//Proc of IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE Press, 2016: 2454-2461.
[12]Liang Jing, Guo Qianqian, Yue Caitong, et al. A self-organizing multi-objective particle swarm optimization algorithm for multimodal multi-objective problems[C]//Advances in Swarm Intelligence: Proc of the 9th International Conference. Berlin: Springer, 2018: 550-560.
[13]Lin Qiuzhen, Lin Wu, Zhu Zexuan, et al. Multimodal multiobjective evolutionary optimization with dual clustering in decision and objective spaces[J]. IEEE Trans on Evolutionary Computation, 2021, 25(1): 130-144.
[14]Hu Zhongbo, Zhou Ting, Su Qinghua, et al. A niching backtracking search algorithm with adaptive local search for multimodal multiobjective optimization[J]. Swarm and Evolutionary Computation, 2022, 69: article ID 101031.
[15]Zhang Kai, Shen Chaonan, Yen G G, et al. Two-stage double niched evolution strategy for multimodal multiobjective optimization[J]. IEEE Trans on Evolutionary Computation, 2021, 25(4): 754-768.
[16]Fan Qinqin, Yan Xuefeng. Solving multimodal multiobjective problems through zoning search[J]. IEEE Trans on Systems, Man, and Cybernetics: Systems, 2021, 51(8): 4836-4847.
[17]Fan Qinqin, Ersoy O K. Zoning search with adaptive resource allocating method for balanced and imbalanced multimodal multi-objective optimization[J]. IEEE/CAA Journal of Automatica Sinica, 2021, 8(6): 1163-1176.
[18]Ji Hebing, Chen Shaojie, Fan Qinqin. Zoning search and transfer learning-based multimodal multi-objective evolutionary algorithm[C]//Proc of IEEE Congress on Evolutionary Computation. Pisca-taway, NJ: IEEE Press, 2022: 1-8.
[19]Fan Jiajia, Huang Wentao, Jiang Qingchao, et al. A zoning search based multimodal multi-objective brain storm optimization algorithm for multimodal multi-objective optimization[J]. Algorithms, 2023, 16(7): article ID 350.
[20]Liu Qingqing, Cui Caixia, Fan Qinqin. Self-adaptive constrained multi-objective differential evolution algorithm based on the state-action-reward-state-action method[J]. Mathematics, 2022, 10(5): article ID 813.
[21]Yue Caitong, Qu Boyang, Yu Kunjie, et al. A novel scalable test problem suite for multimodal multiobjective optimization[J]. Swarm and Evolutionary Computation, 2019, 48: 62-71.
[22]Yue Caitong, Suganthan P N, Liang Jing, et al. Differential evolution using improved crowding distance for multimodal multiobjective optimization[J]. Swarm and Evolutionary Computation, 2021, 62: article ID 100849.
[23]Liang Jing, Qiao Kangjia, Yue Caitong, et al. A clustering-based differential evolution algorithm for solving multimodal multi-objective optimization problems[J]. Swarm and Evolutionary Computation, 2021, 60: article ID 100788.
[24]Qu Boyang, Li Chao, Liang Jing, et al. A self-organized speciation based multi-objective particle swarm optimizer for multimodal multi-objective problems[J]. Applied Soft Computing, 2020, 86: article ID 105886.
[25]Hu Yi, Wang Jie, Liang Jing, et al. A two-archive model based evolutionary algorithm for multimodal multi-objective optimization problems[J]. Applied Soft Computing, 2022,119: article ID 108606.
[26]Zitzler E, Thiele L. Multiobjective optimization using evolutionary algorithms—a comparative case study[J]. IEEE Trans on Evolutio-nary Computation, 1999, 3(4): 257-271.
[27]Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Trans on Evolutionary Computation, 2002, 6(2): 182-197.
[28]Zhou Aimin, Zhang Qingfu, Jin Yaochu. Approximating the set of Pareto-optimal solutions in both the decision and objective spaces by an estimation of distribution algorithm[J]. IEEE Trans on Evolutionary Computation, 2009, 13(5): 1167-1189.
[29]Shi Yuhui. Brain storm optimization algorithm[C]//Advances in Swarm Intelligence: Proc of the 2nd International Conference. Berlin: Springer, 2011: 303-309.
[30]Cheng Shi, Qin Quande, Chen Junfeng, et al. Brain storm optimization algorithm: a review[J]. Artificial Intelligence Review, 2016, 46(4): 445-458.
[31]魏诗雨, 刘勇. 机器人路径规划的新型头脑风暴优化算法[J]. 计算机应用研究, 2022,39(2): 402-406. (Wei Shiyu, Liu Yong. Robot path planning with novel brain storm optimization algorithm[J]. Application Research of Computers, 2022, 39(2): 402-406.)
[32]胡洁, 范勤勤, 王直欢. 融合分区和局部搜索的多模态多目标优化[J]. 智能系统学报, 2021,16(4): 774-784. (Hu Jie, Fan Qinqin, Wang Zhihuan. Multimodal multi-objective optimization combining zoning and local search[J]. CAAI Trans on Intelligent Systems, 2021, 16(4): 774-784.)
[33]Wilcoxon F. Individual comparisons by ranking methods[J]. Biometrics Bulletin, 1945, 1(6): 80-83.
[34]Friedman M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance[J]. Journal of the American Statistical Association, 1937, 32(200): 675-701.

