基于自适应平衡静动态联合网络的公交客流预测

摘 要：为解决现有公交客流预测方法多数利用预定义的图结构进行空间建模，对交通状况变化所引起客流波动考虑不充分，无法捕捉短时动态的空间依赖关系问题，提出一种自适应平衡静动态联合网络（ASDNet）模型。首先，利用时间卷积网络捕获序列的时间相关性；其次，利用图卷积捕捉站点之间整体空间信息，采用动态图同构网络捕捉相邻时隙动态图之间隐藏的动态依赖关系；最后，通过自适应平衡机制自适应地调节静动态联合网络之间的信息传递。在广州市真实公交数据集上进行了实验，结果表明，与多个基准模型相比，该模型在MAE、RMSE和MAPE预测误差指标上平均降低了12.2%、9.9%和15%，R2精确度指标上平均提高了6.3%。表明该模型能够有效地捕捉客流数据的时空变化规律，可为公交运营管理提供技术参考。

关键词：公交客流预测； 时间卷积网络； 图卷积； 动态图同构网络； 自适应平衡静动态联合网络； 时空变化

中图分类号：TP183 文献标志码：A

文章编号：1001-3695（2024）08-016-2360-06

doi：10.19734/j.issn.1001-3695.2023.12.0589

Bus passenger flow prediction based on adaptive equilibriumstatic and dynamic joint network

Huang Lai’an， Zhu Hangxiong， Li Bo

（School of Automation， Guangdong University of Technology， Guangzhou 510006， China）

Abstract：To address the limitations of existing public transit passenger flow prediction methods， which often rely on predefined graph structures for spatial modeling， inadequately consider fluctuations in passenger flow caused by changes in traffic conditions， and fail to capture short-term dynamic spatial dependencies， this paper proposed an adaptively balanced static-dynamic joint network（ASDNet） model. Firstly， the model used a temporal convolution network to capture the temporal correlation of sequences. Secondly， it employed graph convolution to capture the overall spatial information between sites， and then incorporated a dynamic graph isomorphic network to capture the hidden dynamic dependencies between dynamic graphs of neighboring time slots. Finally， it introduced an adaptively balanced mechanism to adjust the information transfer between static-dynamic joint networks. The model tested a real bus dataset derived from Guangzhou city. The results demonstrate that the model reduces the MAE， RMSE， and MAPE prediction error metric by an average of 12.2%， 9.9%， and 15%， respectively， and improves the R2 accuracy metric by an average of 6.3% compared to several benchmark models. These results indicate that the model can effectively capture the spatiotemporal variation law of passenger flow data and provide technical reference for bus operation management.

Key words：public transit passenger flow prediction; temporal convolutional network; graph convolution; dynamic graph isomorphic network; adaptively balanced static-dynamic joint network; spatial-temporal variation

0 引言

随着各城市公共交通健康可持续发展的全面推进，协助管理者优化公交资源配置和规划对促进公交服务提质增效愈发重要［1］。公交客流预测是利用历史客流量及其相关信息来预测未来一段时间内的客流量，是公交企业对车辆合理调度与线路优化的重要依据［2］。如何精准预测公交客流已逐渐成为公交运营管理的重难点问题。

公交客流量预测根据实际预测目标可分为区域流量预测［3］、线路流量预测［2］和站点流量预测［4］。区域预测通过分析城市区域特征，预测每个区域的客流量分布，无法捕捉不同区域交通流量的空间异质性和交通模式随时间变化的时间异质性，影响实际客流预测的准确性。线路流量预测通过分析某段时间内的线路客流量数据变化，捕捉交通线路之间的时空特征，可以相对提升客流预测的准确性。但公交客流中的预测未来值是整体和局部信息共同作用的结果，实际公交运行时的客流量受天气、时间、交通实时状况等因素影响。站点客流预测通过分析客流数据，利用线路、区域间的全局空间信息，并考虑站点短时间范围内局部空间动态信息的变化，可以进一步提高公交客流预测模型的鲁棒性和准确性。

针对公交客流预测问题的研究，其主要步骤分为空间路网拓扑构造、时间相关性研究和空间相关性研究等［5，6］。

a）空间路网拓扑构造。利用深度神经网络结合传统网格的方法提取时空信息，描述路网空间结构，即卷积神经网络（convolutional neural network，CNN）［7］学习空间关系，递归神经网络（recurrent neural network，RNN）［8］捕捉时间依赖。如Zhang等人［3］提出ST-ResNet模型将城市划分为网格地图，用CNN分层捕获空间结构信息，使用残差神经网络框架来建模人群交通的时间距离、周期和趋势属性。而路网公交站点的分布是一种拓扑网络结构，并非标准的网格结构分布，因此无法充分挖掘不同线路、站点之间的非线性空间依赖关系［9］。利用图神经网络（graph neural network，GNN）处理图拓扑［10，11］及非欧氏空间数据，基于邻接矩阵方法构造不同类型的空间路网拓扑图，可以较好地处理空间异质性。因此成为目前交通预测领域的流行方法，取得了比基于网格方法更好的性能［12，13］。

b）时间相关性研究。指对时间序列数据进行建模，捕捉数据之间的时间相关依赖关系。常用方法有RNN、门控递归单元（gated recurrent unit，GRU）、长短期记忆网络（long short-term memory，LSTM）［14］和时间注意力机制［15］。除这些方法外，还有Transformer模型以及时间卷积网络（temporal convolution network，TCN）［16］。如Cai等人［17］直接应用谷歌的Transformer机器翻译框架来预测交通流量，可以捕捉时间序列的连续性和周期性；王璨等人［18］提出了时间卷积知识跟踪模型（TCN-KT），利用了TCN在处理时间序列数据方面的优势，有效地提高了模型效率。由于TCN利用CNN处理高维数据的优势，可以并行处理不同长度和采样率的时间序列数据，具有更高的效率，所以本文采用具有门控机制的TCN来捕获时间相关性。

c）空间相关性研究。主要指对站点信息等空间位置数据进行建模，捕捉站点空间关系。较流行方法主要有图卷积网络（GCN）［19］、图注意力网络（graph attention network，GAT）及各种变体网络［20］。其中GCN具有从相邻节点中提取特征并根据不同的数据结构进行灵活调整的优点。Li等人［8］提出的DCRNN模型利用交通图上的双向随机游走来对空间信息进行建模，并通过门控循环单元（GRU）捕获时间动态；Luo等人［21］基于物理邻接和语义相似度构造子图来捕捉公交站/线路之间的空间依赖关系；Liu等人［22］构建物理-虚拟协作图网络模型，将物理拓扑图、相似性图和相关性图输入到图卷积门控循环单元（GC-GRU）中学习时空特征。

以上研究为公交客流预测奠定了良好的基础，但仍存在不足。许多模型利用相似性或距离度量对预定义的图结构数据构造路网拓扑，进而捕捉站点间的时空相关性。然而，它们未充分考虑短时间范围内局部空间信息的影响，无法充分反映客流数据的时空变化规律，如：a）某个站点因为突发事件（交通事故或者临时活动）而临时关闭，乘客无法在该站点上车或下车，这可能会导致周边站点的客流量发生变化；b）在早上上班高峰期和晚上下班高峰期，不同站点的客流情况也会有所不同。

为解决上述问题，本文提出一种自适应平衡静动态联合网络的公交客流预测模型（adaptive balanced static-dynamic joint network for bus passenger flow prediction model，ASDNet），该模型使用门控扩张因果卷积提取时间相关性，使用扩散图卷积［8］捕捉公交站点之间的全局空间信息，使用动态图同构网络［23］捕获不同站点之间以及相邻时隙之间隐藏的动态依赖关系，并增强图学习的有效性，其目的是挖掘实时客流量与路况变化引起的局部空间信息。然后利用平衡融合机制去平衡扩散图卷积与动态图同构网络的影响。本文的主要贡献如下：

a）通过图卷积来有效捕捉公交站点之间全局空间信息，使用一个动态图构建模块与学习模块，充分考虑局部信息的动态特性，挖掘节点属性中的相关信息来描述客流量的突然波动。

b）引入一种改进的动态图同构网络，其核心是通过并行化实现动态范式表示不同时隙数据间的信息联系，解决动态GNN由于在动态图转换后完全分离同一维度中不同时隙数据，导致难以捕捉相邻时隙之间隐藏的动态依赖关系的问题，从而提升模型对不同时隙数据图结构的判别和表示能力。

c）提出一种自适应平衡融合机制，自适应调节静态信息和动态信息在公交客流预测中的影响，提升模型对短时间内突发事件的适应能力。实验结果表明，该模型在真实公交数据集上预测公交客流方面具有有效性。

1 问题定义

实际公交系统的站点分布和客流分布通常呈现不规则拓扑结构，且站点间客流量分布与不同站点间的功能性和地理连接性呈现相关性。利用这种非欧关系，进行不同站点的客流预测。

定义带权重的有向图G=（V，E，A）描述公交路网拓扑结构，其中V表示公交站点的节点集，模值大小表示站点数量，即N=V，E表示站点之间连通性的边集，A∈Euclid ExtraaBpN×N表示任意一对节点之间接近度的加权邻接矩阵。

在每个时间步t，图G表示为图形信号X（t）∈Euclid ExtraaBpN×D，其中D是每个节点的属性维度。公交站点客流预测问题描述为：给定S个历史图信号χ=［X（t-S+1），…，X（t）］∈Euclid ExtraaBpS×N×D和公交路网的邻接矩阵A∈Euclid ExtraaBpN×N，通过模型函数f学习预测未来T个图信号=［X^（t+1），…，X^（t+T）］∈Euclid ExtraaBpT×N×F各站点上车客流量，其映射关系表示如下：

［χ，A］f（1）

其中：期望尽可能接近真实值y。

2 自适应平衡静动态联合网络的公交客流预测模型

本文模型总体框架如图1（a）所示，主要由输入模块、多个时空层和输出模块组成。首先，通过输入模块对历史客流数据进行转换，然后传输到时空层。在每个时空层中，为了避免梯度消失的问题，在输入端和输出端之间使用残差连接，并将其用作下一个时空层的输入特征。最后，通过跳跃连接将每个时空层的输出信息传输到输出模块，从而得到预测结果。

时空层如图1（b）所示，主要由时间模块、空间模块、动态图构造与学习模块和路网结构组成。时间模块由两个并行的时间卷积和一个门控机制组成，用于从输入模块数据中提取时间相关性特征，并将信息传输给空间模块。空间模块由图卷积（S-GCN）、动态图同构网络（D-GIN）和平衡门组成，在路网结构与动态图构造方面，分别使用图卷积（S-GCN）和动态图同构网络（D-GIN）提取整体空间特征与局部空间特征，两者经过平衡门融合作为整个时空层的输出。

2.1 输入输出模块

输入模块将每个节点每个时刻对应的客流数据的时刻特征加入到客流数据中，公式定义为

It=conv1×1（Xt‖Tt）（2）

其中：It∈Euclid ExtraaBpB×N×Din为数据增加一个一天中的时间特征，Din是特征维度，B是批量大小，N是节点数;Xt是客流数据，Tt为一天中的时间。

输出模块将隐藏的特征投影到所需的维度以获得最终结果。

2.2 时间卷积模块

本文在时间卷积模块使用扩张因果卷积网络，通过增加层的深度实现指数级较大感受野，向输入填充零来保留时间因果顺序，方便从节点历史属性中捕获时间趋势及依赖关系，从而简化并行计算，节省计算资源，缓解梯度爆炸或消失问题。为提升时间卷积网络层模块信息流的传递效率和准确性，本文在扩张因果卷积网络基础上引入一种门控机制，将两个输入X′i，1，X′i，2经过不同函数激活，再进行元素相乘，其定义如下：

hi=δ（Θ1X′i，1+b）⊙tanh（Θ2X′i，2+c）（3）

其中：Θ1、Θ2、b和c表示模型参数；hi表示第i个节点的时间卷积模块输出；δ（·）表示决定传递到下一个模块信息比率的sigmoid函数，用来消除tanh（·）中的无关信息，选择更重要的信息；⊙表示Hadamard乘积。

2.3 图卷积模块

将公交线路及其站点抽象为一个图结构，利用扩散卷积层可以更有效捕捉空间相关性。在实际公交运营中，公交行驶分为上行和下行，路网建模本质为有向图结构，利用扩散卷积模拟双向扩散过程，使模型能够捕捉上游和下游流量的影响，其扩散图卷积层定义：

Z=∑Kk=0PkfXθk1+PkbXθk2（4）

其中：前向转换矩阵为Pf=D-1oA，后向转换矩阵为Pb=D-1lAT；D是一个对角矩阵，对角线上的第i个元素表示第i个节点的度数Dii=∑jAij；Z表示输出；k表示扩散步长；θ表示模型参数矩阵。

2.4 动态图构造与学习模块

图节点间关系在全局上相对稳定，但图中局部节点的空间关系易受早高峰、天气状况或交通事故等交通突发事件影响。考虑到节点与记录客流量属性之间存在相关性，本文通过挖掘节点属性中的相关信息来描述客流量的突然波动。

本文利用动态图构造模块生成图邻接矩阵，通过“浅层”嵌入对邻接矩阵进行编码，用于表示节点变量之间隐藏的依赖关系。通过训练进行迭代优化，来学习局部信息的动态特性。图的构造定义如下：

=T·γ（5）

idx，idy=arg topk（［：，：］） idx≠idy（6）

［-idx，-idy］=0（7）

其中：=［t，1，t，2，…，t，l］，γ=［γt，1，γt，2，…，γt，l］表示可学习节点嵌入的随机初始化;arg topk（·）返回邻接矩阵前k个最大值的指数。对于每个时隙的邻接矩阵，只保留权重最大的前k个元素，其他值均设为零。

2.5 改进动态图同构网络模块

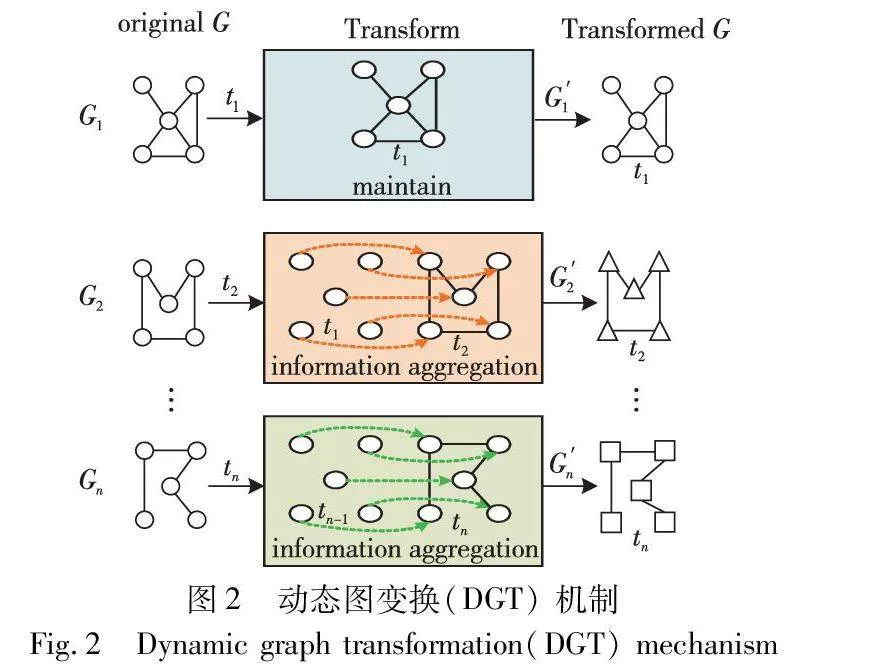
动态图神经网络通过传递和聚合节点特征信息来处理不同时间序列维度之间的空间关系，获得节点间的作用关系，实现动态图节点信息的传播。为描述不同时隙动态图节点之间的关联转换，本文建立动态图转换机制（如图2所示），描述定义如下：对于每个时隙图，除首个时隙图外，添加相同数量的顶点，分别代表对应顶点前一个时隙图的数据。顶点集将被修改为{v（t，1），v（t，2），…，v（t，n），v（t-1，1），v（t-1，2），…，v（t-1，n）}。将前一个时隙顶点的方向（即有向边）赋给当前时隙的对应点，意味着在N=1，2，…，n的情况下，添加从v（t-1，n）到v（t，n）的连接，进而生成一组新动态图用于进行下一操作。

与静态GNN相比，动态GNN在DGT之后完全分离同一维度中的不同时隙数据，但实际上不同时隙的同一顶点通常会聚合来自不同顶点集的信息。而在平均相邻图中，相比于其他动态GNN变体，图同构网络（GIN）具有区分不同图的局部拓扑结构的优点。为此本文通过改进动态图同构网络（DyGIN），引入动态图同构权重聚合机制，提升模型对不同时隙数据图结构的判别和表示能力。具体地，某个图节点vi在t时刻的图同构算子表示为

x（i，k）t=MLP（k）（（1+ε（k））·x（i，k-1）t+∑j∈N（i）ij·x（j，k-1）t+x（i，k-1）t-1）（8）

其中：x（i，k）t表示节点vi在k层中时间t的输出;x（i，k-1）t-1是动态图变换的简单实现，表示聚合首个时隙图后的数据;边缘权重ωij归一化为ij;ε（k）是一个可学习的参数，表示同一节点vi从前一层获得的相当大的激活量的百分比。

进一步，设计一种新的聚合方法，通过并行化动态范例来表示不同时隙数据间的信息联系，公式定义如下：

x（i，k）=concat（x（i，k）tt=0，1，…，T）（9）

2.6 自适应平衡融合机制模块

为了充分合理利用静态信息和动态信息特征，形成更全面合理的公交客流图，本文提出一种自适应平衡融合机制，通过学习加权系数来确定静态信息和动态信息的重要性，自适应调节静态图和动态图的影响，其公式定义如下：

Z=sigmoid（WsXs+WdXd）（10）

其中：Ws和Wd是可训练参数；Xs和Xd分别代表静态图与动态图做图卷积的结果。sigmoid函数看作是一个门控函数，表示将张量Z的值映射到0～1，通过控制平衡门的开启程度，自适应调整静态图和动态图之间的权衡程度。

3 实验

3.1 数据集

本文测试数据选取的是广州市2023年3月1日至4月30日的公交IC卡刷卡数据，如表1所示，其中包含刷卡时间、卡片ID、卡类型、交易金额、线路名称、站点名称和站点顺序等信息。目前，广州是采用“一站计价制”票制，即乘客搭乘公交上车时一次刷卡，到达目的地下车时无须二次刷卡。越秀区作为广州最古老的中心城区，承载了大量的客流需求，此外其交通环境复杂多变，站点客流变化受街区分布影响。因此，本文选取越秀区207个主要站点的上车客流作为本次研究的目标对象，来充分验证本文模型在站点级客流预测任务上的有效性。其站点实际分布如图3所示。

3.2 数据处理

根据各个公交线路的正常运营时间，本文排除6：00之前和22：30之后的记录，并以5 min为间隔对各个公交站点不同时间段的客流数据进行统计，最终获得了8 557条记录作为数据集，并按照时间顺序进行拆分，70%的数据用于训练，20%用于测试，其余10%用于验证。所有实验均使用z-score标准化方法对客流数据进行预处理。节点的预定义邻接矩阵由站点之间的距离和阈值高斯核构成［14］。预定义邻接矩阵A可以定义如下：

Avi，vj=exp（-d2vi，vjσ2） exp（-d2vi，vjσ2）≥ε0其他情况（11）

其中：dvi，vj是站点vi到vj之间的距离，根据站点的经纬度计算所得;σ是距离的标准差，控制矩阵A的分布;ε是控制矩阵A稀疏性的阈值。

3.3 参数设置

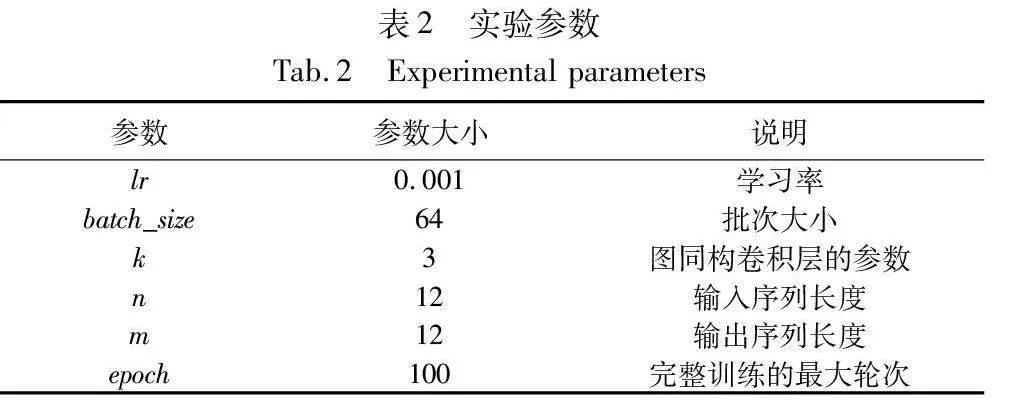
本文基于PyTorch框架在RTX3090 GPU上对本文模型进行训练。本文所有实验均使用60 min的历史数据来预测未来15 min、30 min和60 min的客流量。由于Adam增加了自适应学习率机制，可以为不同的参数分配不同的学习率，使得训练过程可以更快地收敛［24］。因此，该模型使用Adam优化器，实验参数设置如表2所示。

为了覆盖输入序列的长度，使用4个时空块和膨胀因子序列为1、2。针对模型在训练过程中需要进行一步预测，而在推理过程中需要进行多步预测导致训练和测试不一致的问题，本文选用平均绝对误差（MAE）作为模型训练目标，定义客流预测的损失函数为

L（X，X^）=1T×N×D ∑i=Ti=1∑j=Nj=1∑k=Dk=1Xi，j，k-X^i，j，k（12）

其中：T是时间步，N是节点数量，D是特征维度。Xi，j，k和X^i，j，k是真实值和预测值。

3.4 比较算法与评估指标

a）历史平均模型（HA）［25］。利用历史时期的平均流量信息作为预测。

b）门控循环单元（GRU）［26］。它是RNN的一种变体模型，也是一种基于深度学习的时间序列预测方法。

c）图波网络（Graph WaveNet）［27］。它是一个基于GNN和CNN的模型。通过构造自适应依赖矩阵捕捉隐藏的空间依赖关系，并使用扩张一维卷积处理长时间序列。

d）多元时间图神经网络（MTGNN）［28］。它是一个基于GNN 和CNN的模型。通过自适应图来学习变量间的依赖关系，并使用混合跳传播层和扩张初始层表捕获时空相关性。

e）自适应图卷积递归网络（AGCRN）［29］。它是一种基于GNN和RNN的模型。将GRU和图卷积在时间和空间上相互结合，形成了一种自适应图卷积循环网络去捕捉空间和时间上的相关性。

f）自适应时空图神经网络（Ada-STNet）［30］。它是一种基于GNN和CNN的模型。从宏观和微观两个角度获得最优图邻接矩阵，并通过专用的时空卷积结构捕捉复杂的时空相关性。

g）动态图卷积递归网络（DGCRN）［6］。它是一种基于GNN和RNN的模型。通过节点嵌入过滤生成动态图，并与预定义的静态图相结合，对动态图的精细拓扑进行建模。

实验选用平均绝对误差（MAE）、均方根误差（RMSE）、平均绝对百分比误差（MAPE）和决定系数（R2）指标评价模型性能，分别用于度量预测结果的准确性、离散度、相对误差和拟合程度。各指标定义如下：

MAE=1n∑ni=1xi-i（13）

RMSE=1n∑ni=1（xi-i）2（14）

MAPE=1n∑ni=1xi-ixi（15）

R2=1-∑ni=1（xi-i）2∑ni=1（xi-）2（16）

其中：xi为真实值;i为预测值;为真实值的平均值;n为观测样本的总数，本文设为12。上述指标大小反映了实际值和预测值之间的差异、模型的预测精度以及模型拟合程度，通过使用这些指标，可以客观地比较和评估各种方法的性能，以确定在流量预测任务中表现最佳的方法。其中：MAE、RMSE和MAPE的值越小表示模型的预测能力越好；R2的值越大表示预测能力越好。

3.5 实验结果分析

表3展示了不同模型在公交数据集上未来15 min、30 min和60 min预测的性能。*表示数值小到可以忽略不计，表明模型的预测效果较差。从表3可以看出，与2个经典时间序列模型（HA、GRU）相比，ASDNet在15 min预测任务中RMSE分别降低了8.7%和8.0%，可以看出，经典时间序列模型的预测结果较差，这可能是因为经典时间序列模型通常只关注时间维度上的数据模式和趋势，而忽略了空间维度上的相关性和影响。但与HA的R2相比，ASDNet在15 min预测任务中降低了2.2%，在60 min预测任务中高了7.9%，这可能是因为HA在波动较小的短期数据中预测得更好，但难以处理长期、非平稳的时间序列数据。

此外，与同时考虑时间和空间相关性的模型（Graph WaveNet、MTGNN、AGCRN、Ada-STNet和DGCRN）相比，ASDNet在15 min预测任务中RMSE分别降低了1.0%、0.6%、1.1%、0.8%和0.8%。其中，与MTGNN相比，RMSE的降幅最小，但是在60 min预测任务中RMSE高了48.5%，这可能是因为MTGNN只构造自适应图来捕捉交通网络中不同节点之间的空间关系，而没有考虑整个路网的全局空间信息，导致模型在长时间预测时存在一定的局限性。值得注意的是，ASDNet在三种评估指标的短期和长期预测任务中都取得了最佳的预测性能，这主要得益于其充分考虑了图结构的静态性和动态性，充分利用整体空间信息（长期稳定）和局部动态特性（短期波动）进行预测。

为了更直观地说明模型的预测能力，绘制了MAE和RMSE每个预测步长的变化趋势，如图4所示。从图中可以看出，随着预测步长的增加，其他基准模型的MAE和RMSE比本文ASDNet增长更快，且ASDNet的增长趋势更平缓，在短期和长期预测都表现更好。

在捕捉隐藏空间依赖关系方面，Graph WaveNet具有独特优势。图5绘制ASDNet与Graph WaveNet在6：00～22：30时间段内预测值与真实值对比曲线，发现引入动态图构造学习局部信息的动态特性的ASDNet曲线更平滑，其结果更加拟合真实值曲线，相对Graph WaveNet具有更强的鲁棒性。此外，ASDNet在捕捉短时隐藏动态依赖关系的性能方面优于Graph WaveNet，尤其在晚高峰时段（下午17：00～19：00）可能出现突发交通事件，ASDNet可以更好地预测和捕捉各站点客流相关性变化。

3.6 消融实验

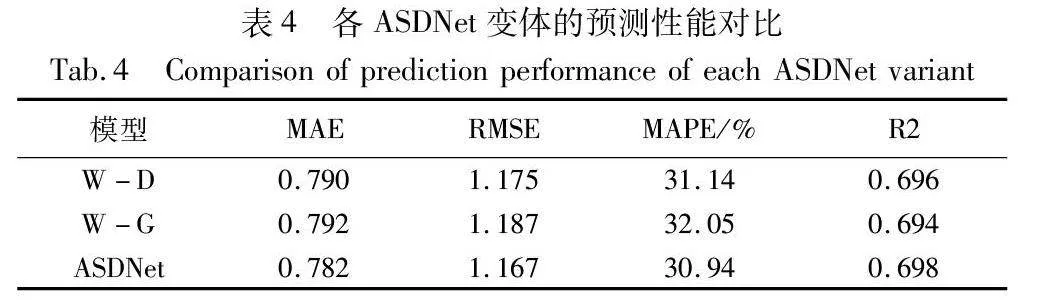
为了进一步验证本文模型中各个模块的有效性，使用如下模型变体进行对比：a）W-D，移除动态图同构网络模块；b）W-G，移除图卷积模块。具体实验结果如表4所示，ASDNet比变体a）和b）的RMSE分别降低了 0.68%、1.68%。结果表明：动态图同构网络模块有助于模型挖掘客流的瞬时波动，图卷积模块可有效捕获站点之间的全局空间信息。通过自适应平衡融合机制，弥补两者之间空间特征的不足，实现更准确的客流预测。

3.7 静态图与动态图区别

静态和动态图模拟的模式不同。静态图侧重于整体空间模式，通过考虑每个节点自身特征，图卷积可以有效地学习整体空间信息，如图6（a）对角线所示。在图6（b）中，发现动态图没有表现出节点的自身特征，而是几条明显的垂直线。这表明动态图的重点在于站点之间的关联性，能有效地捕捉站点之间的局部空间信息。

4 结束语

针对现有公交客流预测方法未能全面挖掘公交路网空间信息的问题，本文提出了基于自适应平衡静动态联合网络的模型。该模型通过扩张因果卷积捕捉节点的时间相关性，进一步利用图卷积捕捉站点之间静态空间信息，动态图构建与学习模块和动态图同构网络捕捉不同变量以及相邻时隙之间隐藏的动态依赖关系，并利用自适应平衡机制调节静态信息和动态信息的权重影响，提升模型对短时间内突发事件的适应能力。在广州公交真实数据集上进行验证，结果表明本文模型具有较好的预测精度和鲁棒性，评估指标基本优于其他基线算法。下一步将融合多源数据特征，提取不同尺度的时间相关性，进行相关的公交客流预测研究。

参考文献：

［1］中华人民共和国交通运输部. 关于推进城市公共交通健康可持续发展的若干意见［J］. 交通财会， 2023（11）： 91-93. （Ministry of Transport of the People’s Republic of China. Several opinions on promoting the healthy and sustainable development of urban public transportation［J］. Finance & Accounting for Communications， 2023（11）： 91-93.）

［2］张伟， 朱凤华， 陈圆圆， 等. 基于注意力机制和分时图卷积的公交客流预测［J］. 模式识别与人工智能， 2021， 34（2）： 167-175. （Zhang Wei， Zhu Fenghua， Chen Yuanyuan， et al. Bus passenger flow forecast based on attention and time-sharing graph convolutional network［J］. Pattern Recognition and Artificial Intelligence， 2021， 34（2）： 167-175.）

［3］Zhang Junbo， Zheng Yu， Qi Dekang. Deep spatio-temporal residual networks for citywide crowd flows prediction［C］//Proc of AAAI Conference on Artificial Intelligence. Palo Alto，CA： AAAI Press， 2017： 1655-1661.

［4］Gong Min， Xiang Fei， Wang Zhihu， et al. Sequential framework for short-term passenger flow prediction at bus stop［J］. Transportation Research Record， 2014， 2417（1）： 58-66.

［5］郭翔宇， 彭莉兰， 李崇寿， 等. 多尺度融合与动态自适应图的公交客流预测模型［J］. 计算机科学与探索， 2024，18（7）：1879-1888. （Guo Xiangyu， Peng Lilan， Li Chongshou， et al. Multi-scale fusion and dynamic adaptive graph bus passenger flow prediction model［J］. Journal of Frontiers of Computer Science and Techno-logy，2024，18（7）：1879-1888.）

［6］Li Fuxian， Feng Jie， Huan Yan， et al. Dynamic graph convolutional recurrent network for traffic prediction： benchmark and solution［J］. ACM Trans on Knowledge Discovery from Data， 2023， 17（1）： 1-21.

［7］Yao Huaxiu， Wu Fei， Ke Jintao， et al. Deep multi-view spatial-temporal network for taxi demand prediction［C］//Proc of AAAI Confe-rence on Artificial Intelligence. Palo Alto，CA： AAAI Press， 2018： 2588-2595.

［8］Li Yaguang， Yu R， Shahabi C， et al. Diffusion convolutional recurrent neural network： data-driven traffic forecasting［EB/OL］. （2018-02-22）. https：//arxiv.org/abs/1707.01926.

［9］Yao Huaxiu， Tang Xianfeng， Wei Hua， et al. Revisiting spatial-temporal similarity： a deep learning framework for traffic prediction［C］//Proc of AAAI Conference on Artificial Intelligence. Palo Alto，CA： AAAI Press， 2019： 5668-5675.

［10］Kipf T N， Welling M. Semi-supervised classification with graph con-volutional networks［EB/OL］. （2017-02-22）. https：//arxiv.org/abs/1609.02907.

［11］Hamilton W L， Ying R， Leskovec J. Inductive representation lear-ning on large graphs［C］//Proc of the 31st International Conference on Neural Information Processing Systems. Red Hook，NY： Curran Associates Inc.， 2017： 1025-1035.

［12］Chen Cen， Li Kenli， Teo S G， et al. Gated residual recurrent graph neural networks for traffic prediction［C］//Proc of AAAI Conference on Artificial Intelligence. Palo Alto，CA： AAAI Press， 2019： 485-492.

［13］Bai Lei， Yao Lina， Kanhere S， et al. STG2Seq： spatial-temporal graph to sequence model for multi-step passenger demand forecasting［C］//Proc of the 28th International Joint Conference on Artificial Intelligence. Palo Alto，CA： AAAI Press， 2019： 1981-1987.

［14］Han Yong， Wang Cheng， Ren Yibin， et al. Short-term prediction of bus passenger flow based on a hybrid optimized LSTM network［J］. ISPRS International Journal of Geo-Information， 2019， 8（9）： 366.

［15］Zhang Qingyong， Li Changwu， Su Fuwen， et al. Spatio-temporal residual graph attention network for traffic flow forecasting［J］. IEEE Internet of Things Journal， 2023， 10（13）： 11518-11532.

［16］Zhao Ling， Song Yujiao， Zhang Chao， et al. T-GCN： a temporal graph convolutional network for traffic prediction［J］. IEEE Trans on Intelligent Transportation Systems， 2019， 21（9）： 3848-3858.

［17］Cai Ling， Janowicz K， Mai Gengchen， et al. Traffic transformer： capturing the continuity and periodicity of time series for traffic forecasting［J］. Transactions in GIS， 2020， 24（3）： 736-755.

［18］王璨， 刘朝晖， 王蓓， 等. TCN-KT： 个人基础与遗忘融合的时间卷积知识追踪模型［J］. 计算机应用研究， 2022， 39（5）： 1496-1500. （Wang Can， Liu Chaohui， Wang Bei， et al. TCN-KT： temporal convolutional knowledge tracking model based on fusion of personal basis and forgetting［J］. Application Research of Compu-ters， 2022， 39（5）： 1496-1500.）

［19］Yu Bing， Yin Haoteng， Zhu Zhanxing. Spatio-temporal graph convolutional networks： a deep learning framework for traffic forecasting［C］//Proc of the 27th International Joint Conference on Artificial Intelligence. Palo Alto，CA： AAAI Press， 2018： 3634-3640.

［20］Guo Shengnan， Lin Youfang， Feng Ning， et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting［C］//Proc of AAAI Conference on Artificial Intelligence. Palo Alto，CA： AAAI Press， 2019： 922-929.

［21］Luo Dan， Zhao Dong， Ke Qixue， et al. Spatiotemporal hashing multigraph convolutional network for service-level passenger flow forecasting in bus transit systems［J］. IEEE Internet of Things Journal， 2021， 9（9）： 6803-6815.

［22］Liu Lingbo， Chen Jingwen， Wu Hefeng， et al. Physical-virtual collaboration modeling for intra-and inter-station metro ridership prediction［J］. IEEE Trans on Intelligent Transportation Systems， 2022， 23（4）： 3377-3391.

［23］Liu Huaiyuan， Liu Xianzhang， Yang Donghua， et al. TodyNet： temporal dynamic graph neural network for multivariate time series classification［EB/OL］. （2023-04-11） . https：//arxiv.org/abs/2304.05078.

［24］Kingma D P， Ba J. Adam： a method for stochastic optimization［EB/OL］. （2017-01-30）. https：//arxiv.org/abs/1412.6980.

［25］Guan Wei. A summary of traffic flow forecasting methods［J］. Journal of Highway and Transportation Research and Development， 2004， 21（3）： 82-85.

［26］Cho K， Van Merrienboer B， Bahdanau D， et al. On the properties of neural machine translation： encoder-decoder approaches［EB/OL］. （2014）.https：//arxiv.org/abs/1409.1259.

［27］Wu Zonghan， Pan Shirui， Long Guodong， et al. Graph WaveNet for deep spatial-temporal graph modeling［C］//Proc of the 28th International Joint Conference on Artificial Intelligence. Palo Alto，CA： AAAI Press， 2019： 1907-1913.

［28］Wu Zonghan， Pan Shirui， Long Guodong， et al. Connecting the dots： multivariate time series forecasting with graph neural networks［C］//Proc of the 26th ACM SIGKDD International Conference on Know-ledge Discovery & Data Mining. New York： ACM Press， 2020： 753-763.

［29］Bai Lei， Yao Lina， Li Can， et al. Adaptive graph convolutional recurrent network for traffic forecasting［J］. Advances in Neural Information Processing Systems， 2020， 33： 17804-17815.

［30］Ta Xuxiang， Liu Zihan， Hu Xiao， et al. Adaptive spatio-temporal graph neural network for traffic forecasting［J］. Knowledge-Based Systems， 2022， 242： 108199.