改进混合粒子群算法求解带时间窗的无人机与车辆协同路径调度问题







摘 要:为提高物流配送效率,考虑时间窗、无人机换电以及无人机多点连续配送等因素,提出了一种带时间窗的车辆与无人机协同配送问题,并设计一种带局部搜索的混合粒子群算法进行求解。该算法以混合粒子群算法为核心,通过构建高效的编解码策略实现了问题解空间到算法搜索空间的转换。进一步,该算法融合单点插入策略、车辆更换策略、无人机更换策略组成局部搜索策略,以此提高算法寻优能力。实验结果表明:所提模型比纯车辆配送的模型效率更高,节省了31.51%的成本;所提算法优于四种对比算法,优化率最高达到82.08%。
关键词:无人机; 车辆调度; 粒子群; 时间窗; 车辆路径问题
中图分类号:TP301 文献标志码:A
文章编号:1001-3695(2024)08-013-2336-07
doi:10.19734/j.issn.1001-3695.2023.12.0608
Improved hybrid particle swarm optimization algorithm for vehiclerouting problem with drone and time window
Ye Liwei1, Wu Junhao1,2, Qi Yuanhang1,2, Luo Haoyu1,2, Huang Gewen3, Wang Fujie4
(1.School of Computer Science, University of Electronic Science & Technology of China, Zhongshan Institute, Zhongshan Guangdong 528402, China; 2.School of Automation, Guangdong University of Technology, Guangzhou 510006, China; 3.Information & Network Center, Jiaying University, Meizhou Guangdong 514015, China; 4.Elite Engineers College of Dongguan University of Technology, Dongguan Guangdong 523808, China)
Abstract:In order to improve the delivery efficiency of logistics, this paper proposed a vehicle routing problem with drone and time window considered by the time window, UAV(unmanned aerial vehicle) power change and multi-point continuous delivery of UAV. Then, this paper proposed a hybrid particle swarm optimization algorithm with local search to solve it. Based on the hybrid particle swarm optimization algorithm, the proposed algorithm transformed the problem solution space into the algorithm search space by constructing an efficient encoding and decoding strategy. Further, the proposed algorithm combined a single point insertion strategy, a vehicle replacement strategy and a UAV replacement strategy to form a local search strategy to improve the optimization ability. The experimental results show that the proposed model is more efficient than the model of pure vehicle distribution and saves 31.51% of the cost. The proposed algorithm is better than the four comparison algorithms, and its highest optimization rate is 82.08%.
Key words:drone; vehicle scheduling; particle swarm; time window; vehicle routing problem
0 引言
随着无人机技术的不断发展,无人机开始被应用于物流配送领域。亚马逊、谷歌、DHL、顺丰等企业相继开展了无人机配送项目的研究及实际应用[1]。但是无人机存在载重能力小、续航时间短、配送距离短等缺点[2]。如何协调无人机与车辆以实现更加高效的配送就成为了当前物流研究的一个热点问题。因此,无人机与车辆联合的车辆路径问题(vehicle routing problem with drone,VRPD)[3,4]应运而生。Murray等人[5]以配送时间最短为目标,建立了两种无人机车辆配送模型。进一步,Ha等人[6]提出车辆无人机协同模型可以降低运营成本。王新等人[7]设计了一种自适应大规模邻域搜索方法,证明了卡车与无人机联合配送的优越性。李妍峰等人[8]则建立了混合整数规划模型,大大降低了运输成本和人力成本。在上述研究中,无人机具有固定的电量,在电量用尽后无法继续配送。因此,部分学者提出无人机可以返回车上进行换电服务的方案,以延长无人机的飞行时间和配送距离。
考虑无人机可换电因素,Raeesi等人[9]建立了时空同步的混合整数线性规划模型,为电动车更换能量耗尽的电池。进一步,颜瑞等人[10]构建了卡车与无人机联合的车辆路径问题的混合整数线性规划模型。范厚明等人[11]则进一步考虑载重、续航、区域路网交通信息等约束建立模型。而在现实配送的过程中,客户会要求货物在指定的时间区间内到达(时间窗),这种情况下的无人机换电时间变得不可忽略。因此,Huang等人[12]提出无人机在返回车辆后需要进行一段时间的恢复才可重新出发。而Di Puglia等人[13]考虑到带时间窗车辆路径问题在物流配送中的广泛应用,建立了以最小化运输成本为目标的数学模型。值得注意的是,文献[12,13]的无人机每次飞行只允许配送1个客户,这并不符合现实的无人机现状。因为随着无人机技术的发展,现有的无人机容量得到了一定提高,并允许在1次飞行中为多个客户服务。
因此,本文考虑了时间窗、无人机换电以及无人机多点连续配送等因素,提出了带时间窗的无人机与车辆协同调度问题(vehicle routing problem with drone and time window,VRPDTW)。不难发现,VRPDTW是一个组合优化问题。针对这类问题,智能算法能在合理的时间内得到一个可行解[14]。因此,本文以混合粒子群算法[15]为核心,构建了快速有效的编解码策略以及局部搜索策略,提出了带局部搜索的混合粒子群算法(hybrid particle swarm optimization with local search strategy,HPSO-LSS)求解VRPDTW。最后,通过实验证明了本文模型及算法的有效性。
1 问题建模
1.1 问题描述
VRPDTW的配送流程为:面对一群有不同货物需求的客户,配送中心向客户提供货物,由一个车队(每台车携带单台无人机)负责在客户规定的时间窗内将货物送达并进行卸货服务。该过程包括:
a)车辆为无人机提供存储货物以及自动换电服务(无须人工操作)。无人机在完成某些客户的配送任务后,回到车辆上自动换电(无人机恢复为其最大续航),可以再从该车辆上起飞并继续为其他客户送货。
b)车辆可在某个节点(配送中心或者客户点)发射或回收无人机。当车辆的无人机起飞后,执行完配送任务将降落到原车辆。
c)车辆和无人机可以同步进行配送服务,即无人机外出执行配送任务时,车辆也可以为其他客户配送货物。
d)如果车辆与无人机将在某一客户点汇合,则默认该客户点使用车辆进行配送,卸货服务时间将从车辆抵达该客户点的时刻开始计算,而无人机的自动换电服务时间则从车辆和无人机汇合的时刻开始计算。在这个过程中,无人机的换电服务以及车辆的卸货服务可以同时进行。此外,车辆需要完成上述两个服务后才能继续前往下一个客户点,而无人机完成换电服务便可以重新起飞。
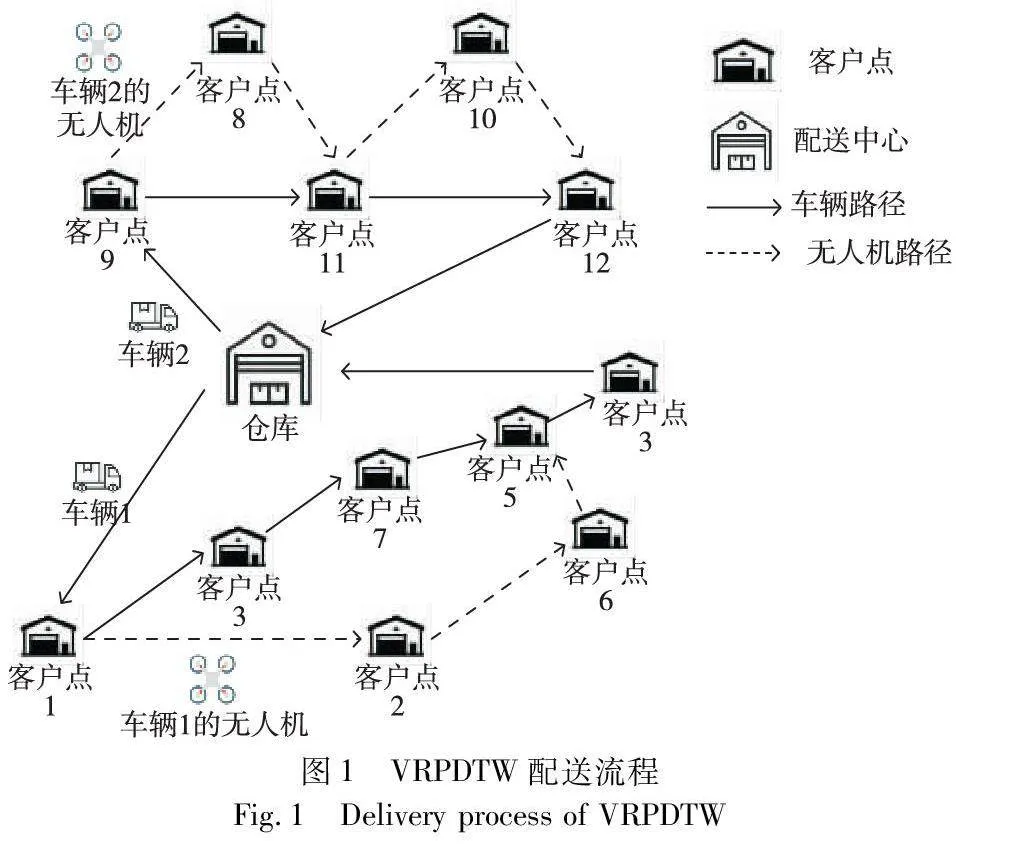
VRPDTW目标在于确定车辆以及无人机的混合配送路径,在满足客户需求的前提下,实现配送成本最小。其配送示意图如图1所示,包含了1个配送中心、2台车辆(每台车携带1台无人机)以及12个客户点。在图1的路径调度方案中,车辆1及其无人机负责配送客户1~7,车辆2及其无人机负责配送客户8~12。
1.2 数学模型
1.2.1 数学变量
1)集合与变量
N为客户集合,N={1,2,…,P},P为客户的数量;N+为客户集合与{P+1}的并集,N+=N∪{P+1};N-为客户集合与{0}的并集,N-=N∪{0};NAll为所有节点集合,NAll=N∪{0,P+1},其中0表示作为起点的配送中心,P+1表示作为终点的配送中心;K为车的数量;k为车的索引,k=1,2,…,K;D为无人机的最大发射次数;d为无人机发射次数索引,d=1,2,…,D;P为客户的数量;p为客户的索引,p=1,2,…,P;w、w′为节点索引,w=0,1,…,P+1,w′=0,1,…,P+1;θ、σ为节点索引,θ=0,1,…,P,σ=1,2,…,P+1;Wk为车辆的最大载重量;Vk为车辆的行驶速度;Ck为车辆配送货物的每公里配送成本;Lk为车辆的最大行驶距离;Wd为无人机的最大载重量;Vd为无人机飞行速度;Cd为无人机配送货物的每公里配送成本;Ld为无人机的最大续航;T为无人机自动换电服务时间;dw,w′为节点w到节点w′的距离;Wp为客户p的货物需求;[tTWSp,tTWEp]:客户p的时间窗,tTWSp和tTWEp为时间窗下限和上限;tSp为客户p的卸货服务时间。
2)决策变量
ek,w,w′:若车辆k经过路径(w,w′),ek,w,w′=1,否则ek,w,w′=0;yk,d,w,w′:若车辆k的无人机第d次航程经过路径(w,w′),yk,d,w,w′=1,否则yk,d,w,w′=0;sp,k:若车辆k服务客户p,sp,k=1,否则sp,k=0
;up,k,d:若车辆k的无人机第d次航程服务客户p,up,k,d=1,否则up,k,d=0;s0k:若车辆k驻留在配送中心,s0k=1,否则s0k=0;uonw,k,d:若节点w为车辆k的无人机第d次航程起飞节点,uonw,k,d=1,否则uonw,k,d=0;uoffw,k,d:若节点w为车辆k的无人机第d次航程降落节点,uoffw,k,d=1,否则uoffw,k,d=0;tAw,k为车辆k到达节点w的时刻,tAw,k≥0;tAw,k,d为车辆k的无人机第d次航程到达节点w的时刻,tAw,k,d≥0;tSp,k,d为车辆k的无人机第d次航程在客户p的服务实际开始时间,tSp,k,d≥0;tAp为客户p处车辆/无人机抵达时间。
1.2.2 目标函数
以最小化配送总成本为目标,本文的目标函数如式(1)所示。
min F=∑k∑w∑w′Ckek,w,w′dw,w′+∑k∑d∑w∑w′Cdyk,d,w,w′dw,w′(1)
其中:第一部分表示车辆总配送成本,第二部分表示无人机总配送成本。
1.2.3 约束条件
首先构建车辆及无人机的载重、行驶距离以及连续性配送的约束,如式(2)~(9)所示。
∑pWpsp,k+∑p∑d(Wpup,k,d)≤Wk k=1,2,…,K(2)
∑w∑w′(ek,w,w′dw,w′)≤Lk k=1,2,…,K(3)
∑p(Wpup,k,d)≤Wd k=1,2,…,K;d=1,2,…,D(4)
∑w∑w′(yk,d,w,w′dw,w′)≤Ld k=1,2,…,K;d=1,2,…,D(5)
∑ksp,k+∑k∑dup,k,d=1 p∈N(6)
s0k+∑pek,p,P+1=s0k+∑pek,0,p=1 k=1,2,…,K;p∈N(7)
∑σek,p,σ=∑θek,θ,p=sp,k k=1,2,…,K;p∈N(8)
∑γ∈S∑γ′∈Sek,γ,γ′≤|S|-1 SN;k=1,2,…,K(9)
其中:式(2)~(5)分别为车辆的载重约束、车辆的最大行驶距离约束、无人机的载重约束与无人机的最大航程约束;式(6)表示每个客户只能由一台车辆或者一台无人机提供服务;式(7)(8)表示每个节点车辆到达的数量需要等于车辆离开的数量;式(9)表示车辆路径不能出现子回路。进一步,定义无人机起飞、飞行、降落的规则,如式(10)~(19)所示。
uoff0,k,d=0 k=1,2,…,K;d=1,2,…,D(10)
uonP+1,k,d=0 k=1,2,…,D;d=1,2,…,D(11)
uon0,k,d=∑pyk,d,0,p k=1,2,…,K;d=1,2,…,D(12)
uoffP+1,k,d=∑pyk,d,p,P+1 k=1,2,…,K;d=1,2,…,D(13)
yk,d,p,p′+sp,k+sp′,k≤2p∈N;p′∈N;k=1,2,…,K;d=1,2,…,D(14)
|(∑σek,w,σ)∑σyk,d,w,σ-(∑θek,θ,w′)∑θyk,d,θ,w′|-Ψ(1-ek,w,w′+s0k)≤0
k=1,2,…,K;d=1,2,…,D;w∈NAll;w′∈NAll(15)
∑σyk,d,p,σ=∑θyk,d,θ,p=up,k,d
p∈N;k=1,2,…,K;d=1,2,…,D(16)
∑w∑σyk,d,w,σ≥δ∑wuonw,k,d
k=1,2,…,K;d=1,2,…,D;δ∈R+(17)
uonp,k,d+∑θyk,d,θ,p=∑σyk,d,p,σ+uoffp,k,dp∈N;k=1,2,…,K;d=1,2,…,D(18)
∑σyk,d,p,σ(∑d′∈D\d∑σyk,d′,p,σ)=0
p∈N;k=1,2,…,K;d=1,2,…,D(19)
其中:式(10)表示配送中心0不能作为无人机的降落点;式(11)表示配送中心P+1只能作为无人机的降落点;式(12)表示车辆携带的无人机如若在配送中心0起飞,则配送中心0为无人机的起飞点;式(13)表示车辆携带的无人机如若在配送中心P+1降落,则配送中心P+1为无人机的降落点;式(14)表示无人机起飞后至少要服务一个客户才能降落回原车辆,式(15)表示无人机从车上起飞后,需要降落在车辆服务的下一个节点;式(16)~(18)表示无人机到达与离开的服务节点数量需要相同;式(19)表示同一无人机不能多次经过同一节点。最后,进行车辆与无人机和时间相关的约束,如式(20)~(29)所示。
tA0,k=0 k=1,2,…,K(20)
tAσ,k≥(tSp,k+tSp+dp,σVk-Ψ(1-sp,kek,p,σ))
σ∈N+;p∈N;k=1,2,…,K(21)
tSp,k≥max{tAp,k,tTWSp}-Ψ(1-sp,k)
p∈N;k=1,2,…,K(22)
tAσ,k≥tA0,k+d0,σVk-Ψ(1-ek,0,σuon0,k,d)σ∈N+;k=1,2,…,K;d=1,2,…,D(23)
tAσ,k≥max{tAθ,k,d,tAθ,k}+T+dθ,σVk-Ψ(1-yk,d,θ,σuoffθ,k,d)
θ∈N-;σ∈N+;k=1,2,…,K;d=1,2,…,D(24)
tA0,k,d=0;k=1,2,…,K;d=1,2,…,D(25)
tAσ,k,d≥tSp,k,d+tSp+dp,σVd-Ψ(1-up,k,dyk,d,p,σ)
σ∈N+;p∈N;k=1,2,…,K;d=1,2,…,D(26)
tSp,k,d≥max{tAp,k,d,tTWSp}-Ψ(1-up,k,d)
p∈N;k=1,2,…,K;d=1,2,…,D(27)
tAσ,k,d≥tAθ,k + dθ,σ Vd -Ψ(1-yk,d,θ,σ uonθ,k,d)
θ∈N-;σ∈N+;k=1,2,…,K;d=1,2,…,D(28)
tAσ,k,d≥max(tAθ,k,tAθ,k,d)+T+dθ,σVd-Ψ(1-yk,d,θ,σuoffθ,k,d)
θ∈N-;σ∈N+;k=1,2,…,K;d=1,2,…,D(29)
其中:式(20)表示车辆从配送中心0出发的时间定义为0时刻;式(21)表示车辆如若在某节点不需要与无人机汇合,则服务完该节点后即可前往下一节点;式(22)表示车辆开始服务客户节点的时刻不可早于客户时间窗的下限;式(23)表示车辆可直接从配送中心0前往下一节点;式(24)表示如若无人机需要与车辆汇合时,车辆需等待无人机换电完成才可前往下一节点;式(25)表示无人机从配送中心0出发的时间定义为0时刻;式(26)表示无人机需要在节点完成服务任务后才可前往下一节点;式(27)表示无人机开始服务客户节点的时间不可早于客户的时间窗下限;式(28)表示无人机需要等待车辆到达节点后才可起飞出发;式(29)表示无人机与车辆汇合后需进行换电服务才可重新出发。
2 算法设计
2.1 混合粒子群算法
在粒子群算法(particle swarm optimization,PSO)中,种群里的每个粒子都有自己的位置、速度以及由优化目标函数决定的适应度值。但是,传统的PSO在粒子搜索的过程中,粒子仅仅学习了个体历史最优值和全局最优值,这容易导致粒子群陷入局部最优,难以求解复杂的组合优化问题[16]。为解决这个问题,Liang等人[15]于2021年提出了一种粒子群算法的改进算法——混合粒子群算法(hybrid particle swarm optimization,HPSO)。HPSO把种群划分为精英子群和跟随子群,以便不同类型的子群能够分别负责不同的搜索任务。精英子群采用一种交叉学习策略,以增强全局搜索能力;而跟随子群则引入了随机粒子学习策略,以提高算法的局部搜索能力。
2.1.1 子种群的划分
根据适应度,升序排列所有的粒子,并根据预设的群体比率λγ来确定两种子群的大小,以此来划分精英子群和跟随子群。HPSO可以通过调节群体比例λγ,进而调节算法的全局搜索和局部搜索能力。
2.1.2 学习策略
1)基于交叉的综合学习策略
在HPSO算法中,每个粒子可能在不同的维度取到最优的值。对于精英种群,本文设计了一种水平交叉算子,可以使两个不同维度的不同粒子之间进行相同维度的交叉操作,进而增强粒子间的相互学习,增加粒子的多样性,提高寻优能力。同时,为了控制搜索空间的大小,使得粒子具有跳脱局部最优的能力,本文设计了一种垂直交叉算子,可以对同一个体最优位置的不同维度进行交叉操作。本文中速度更新公式与传统PSO速度更新公式保持一致,如式(30)所示。水平交叉算子和垂直交叉算子可以在位置更新公式中体现,由γ1取的概率值和λc的比较,决定采用哪种交叉算子来更新粒子的位置,如式(31)所示。
vi,a=ωvi,a+c1r1(pbesti,a-xi,a)+c2r2(gbesta-xi,a)(30)
xi,a=r1pbesti,a+(1-r1)pbestj,a+c(pbesti,a-pbestj,a) γ1≤λcr2pbesti,a+(1-r2)pbesti,bγ1>λc(31)
其中:粒子i的速度vt={vt,1,vt,2,…,vt,a,…,vt,A};粒子i的位置xi={xi,1,xi,2,…,xi,a,…,xi,A};xi和vi的最大维度为A;a、b是xi和vi的任意维度,且a≠b;gbest代表全局最优个体位置;pbesti代表粒子xi的个体最优位置;pbestj代表粒子xj的个体最优位置;ω是惯性权值;c1和c2是加速度系数;c是在[-1,1]均匀分布的随机值;r1、r2、γ1、λc是在[0,1]的随机值。
2)随机粒子学习策略
对于跟随子群,将粒子根据适应度进行排序,适应度较差的粒子排在后面,为引导适应度较差的粒子寻找更优空间,本文设计了一种随机粒子学习策略。假设排序后一粒子xi,前面有i-1个粒子{x1,…,xi-1},随机在这i-1个粒子中抽取一个粒子xe作为适应度较差粒子xi的学习榜样,进行如式(32)所示的交叉运算,生成一个速度矢量。基于该速度矢量,让适应度较差的粒子学习适应度较好粒子的经验,去探索适应度较好粒子的空间,可以得到一个新的粒子位置,如式(33)所示。
vi,a=ωvi,a+c1r1((r2pbesti,a+(1-r2)pbeste,a)-xi,a)(32)
xi,a=pbesti,a+c2r1(gbesta-pbesti,a) γ2≤λm
xi,a+vi,aγ2>λm(33)
其中:粒子i的速度vt={vt,1,vt,2,…,vt,a,…,vt,A};粒子i的位置xi={xi,1,xi,2,…,xi,a,…,xi,A};xi和vi的最大维度为A;a是xi和vi的任意一维度;e是从{x1,…,xi-1}中随机选取的粒子xe的序号;gbest代表全局最优个体位置;pbestj代表粒子xj的个体最优位置;pbeste是较好粒子xe的个体最优位置;ω是惯性权值;c1和c2为加速度系数;r1、r2、γ2、λm是在[0,1]的随机值。
2.2 编解码策略
2.2.1 编码策略
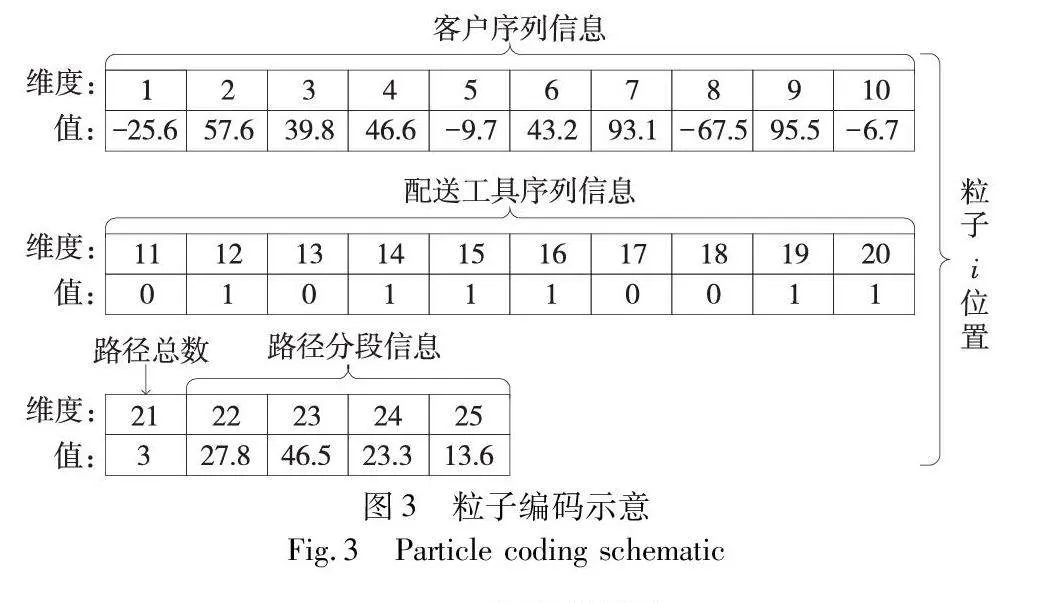
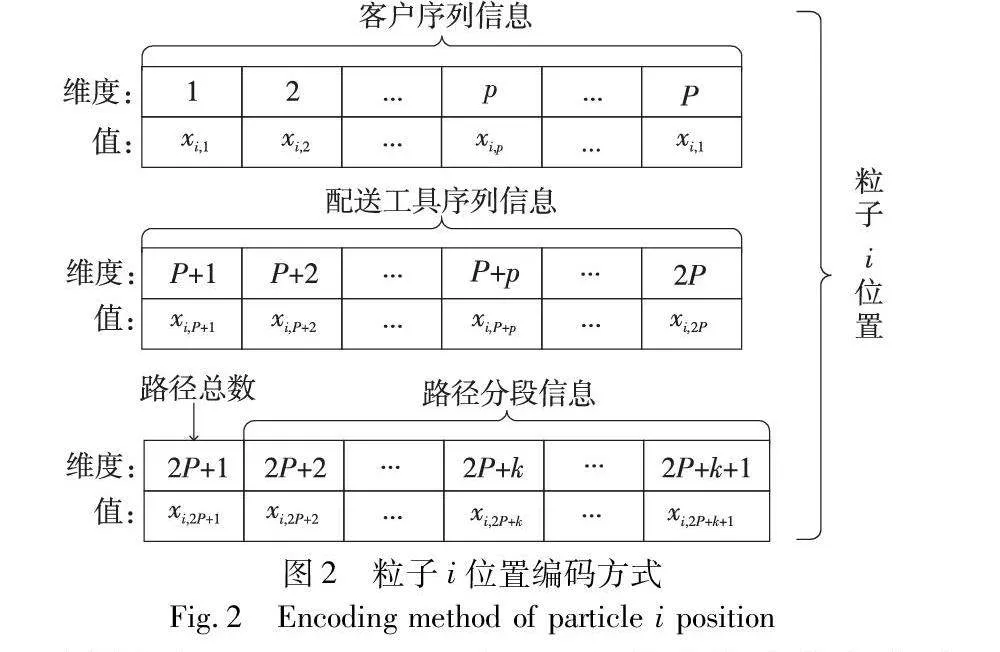
本文设计的粒子位置包含客户序列信息、运载工具序列信息、路径总数和路径分段序列信息四部分信息。假设客户数为P,车的数量为K,每台车上的无人机数量为1,则编码粒子i的位置xi=(xi,1,xi,2,…,xi,2P+K+1)如图2所示。
在图2中,xi,1, … ,xi,P∈[-100,100]代表客户索引; xi,P+1, … ,xi,2P∈{0,1}代表客户对应的配送工具(车辆或无人机); xi,2P+1∈{1,2,…,K}代表实际路径总数(实际使用的车辆数); xi,2P+2, … ,xi,2P+K+1∈[0,100]代表路径分段信息。本文将使用一个具体的例子进行阐述,更好地描述本文的编码策略。假设客户的数量为10、车的数量为4,则粒子的编码如图3所示。图3中粒子i位置的维度为10+10+1+4=25,进而根据编码的取值规则随机便可得到粒子每个维度上的值。接下来将详细介绍粒子的解码方法。
2.2.2 解码策略
为对应上述的编码策略,本文所设计的解码策略包括以下四个步骤:
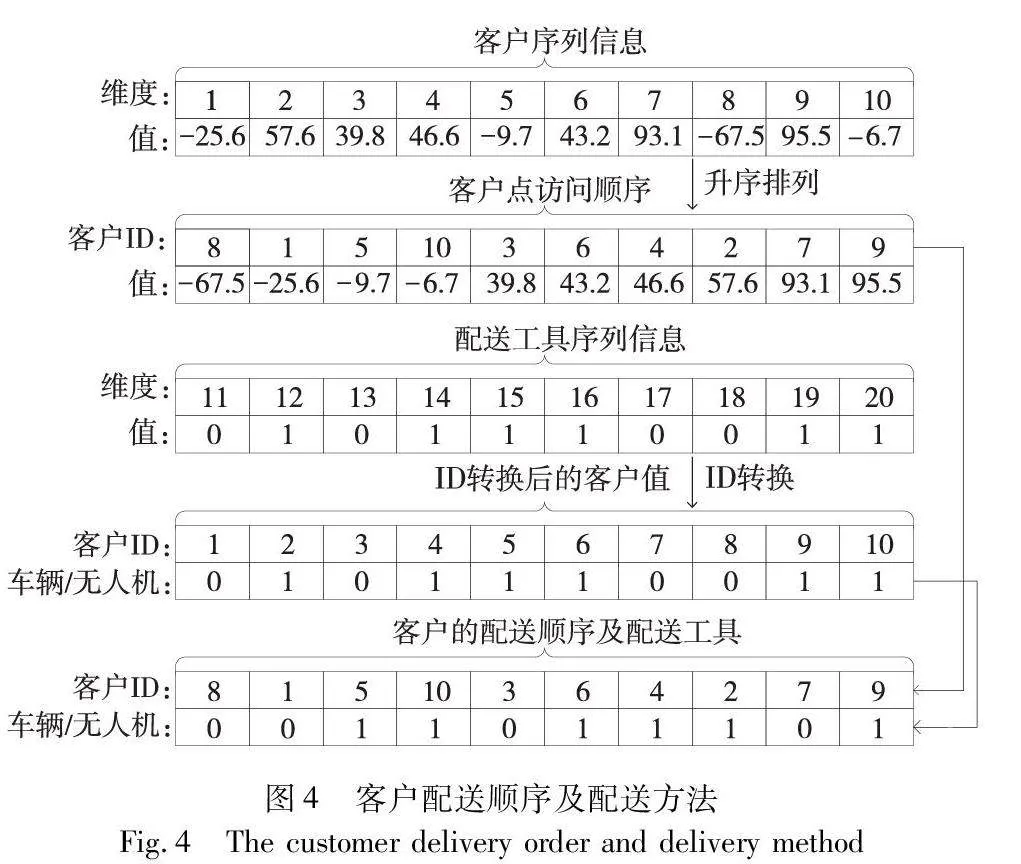
a)获取客户的配送顺序。xi,1,…,xi,P的值分别对应着客户1~P,将xi,1,…,xi,P的值进行升序排列,便能得到对应的客户配送序列xSi。本文将继续沿用图3的例子进行阐述,将图3中粒子前10维度的数据进行升序排列后,得到客户配送序列xSi=(8,1,5,10,3,6,4,2,7,9)。
b)获取客户的配送方法。xi,P+1,…,xi,2P的值分别对应着客户1~P的配送工具选择,xi,P+p=0表示客户p由汽车负责配送,xi,P+p=1表示客户p由无人机进行配送。将客户的对应配送方法与上述所获得的配送序列相匹配结合,便可以得到客户的配送序列与其配送工具的匹配信息。继续沿用图3中的例子,可以得到客户1~P的配送工具序号为(0,1,0,1,1,1,0,0,1,1),接下来将其与配送序列进行匹配结合,可以得到匹配的信息{(8,0),(1,0),(5,1),(10,1),(3,0),(6,1),(4,1),(2,1),(7,0),(9,1)},为直观表明匹配方法,匹配过程如图4所示。从图4可以看出,客户1、3、7和8采用车辆配送;客户2、4、5、6、9、10采用无人机进行配送。
c)获取实际的路径总数以及每段路径的客户数。xi,2P+1的值表示实际的路径总数,同时令λ=xi,2P+1。当λ=1,则表示只有1条路径,所有客户均在这条路径上配送。当λ>1时,需要使用(xi,2P+2,…,xi,2P+M+1)中前λ维计算每段路径的客户数。令路径1,2,…,λ′,…,λ分别对应xi,2P+2,xi,2P+3,…,xi,2P+1+λ′,…,xi,2P+1+λ。对于路径λ′(λ′=1,2,…,λ),其客户数为
cosλ′= xi,2P+1+λ′∑λτ=1xi,2P+1+τ(P-λ)」+1 λ′≠λP-∑λ-1τ=1cOSτλ′≡λ(34)
其中: 」是向下取整数。
由图3可知,xi,21=3表示路径总数为3,cOS1、cOS2和cOS3计算过程如下所示。
cos1= 27.827.8+46.5+23.3×(10-3)」+1=2
cos2= 46.527.8+46.5+23.3×(10-3)」+1=4
cos3=10-2-4=4
在本例子中,由于路径总数为3,因而作为路径4值的xi,25不需要被使用。
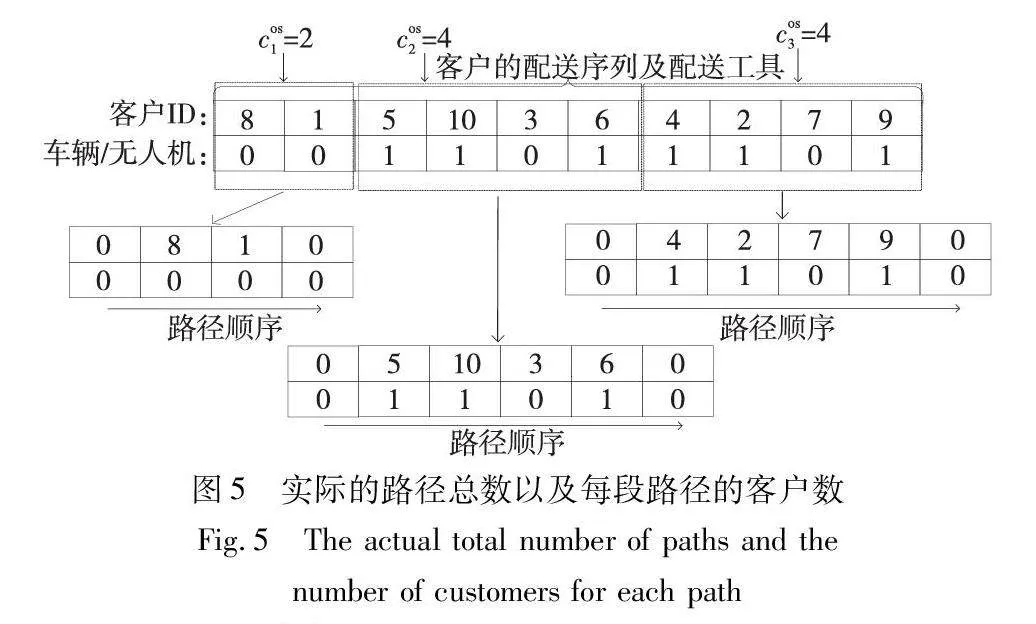
d)获取分段路径信息及具体的配送路径。根据cOS1,cOS2,…,cOSλ的值,从左到右划分客户配送序列,得到临时分段信息。由于所有路径均是从配送中心出发并回到配送中心,进一步在每段临时分段信息的始末加上配送中心“0”,再结合每个节点对应的配送方法(默认配送中心的配送工具为车辆),从而得到最终的分段路径信息,过程如图5所示。
在图5中,分段路径1信息为{(0,0),(8,0),(1,0),(0,0)},分段路径2信息为{(0,0),(5,1),(10,1),(3,0),(6,1),(0,0)},分段路径3信息为{(0,0),(4,1),(2,1),(7,0),(9,1),(0,0)}。根据这些分段信息,易得各个车辆包含其无人机的具体路径。例如,车辆1的配送路径为{(0,0),(8,0),(1,0),(0,0)},其没有应用无人机;车辆2的配送路径为{(0,0),(3,0),(0,0)},其无人机的配送路径包含2条,{(0,0),(5,1),(10,1),(3,0)}、{(3,0),(6,1),(0,0)};车辆3的配送路径为{(0,0),(7,0),(0,0)},其无人机的配送路径包含2条,{(0,0),(4,1),(2,1),(7,0)},{(7,0),(9,1),(0,0)}。获得具体路径后,可根据目标式(1)计算各个粒子的适应度。
2.3 局部搜索策略
局部搜索策略可有效提高算法的搜索能力[17]。因此,本文设计了三种不同的局部搜索策略加强算法的求解能力,分别为随机取点插入策略、随机取点更换运输工具策略和遍历更换无人机策略。
a)单点插入策略:随机取一个客户点及其对应的运输工具插入到另一个客户点前面,从而获得一个新的配送方案。如果配送方案变得更优,则更新配送方案;否则,保持原方案。其中,插入情况包括不同路径间的单点插入、同段路径的单点插入。
b)车辆更换策略:随机取一个客户,将它的运输工具更换为车辆,从而获得一个新的配送方案。如果配送方案变得更优,则更新配送方案;否则,保持原方案。
c)无人机更换策略:随机取一组路径,从第一个客户点开始,从左到右遍0+rKdtGu1+uX+d9J+IPM5ccXV/H6bVWUpaXnU/02E7Y=历地依次更换客户点的运输工具为无人机(若原为使用无人机配送,则无须更换)。如果配送方案变得更优,则更新配送方案;否则,继续更新下一客户点的运输工具,直到该组路径的客户点遍历完毕。
2.4 算法流程
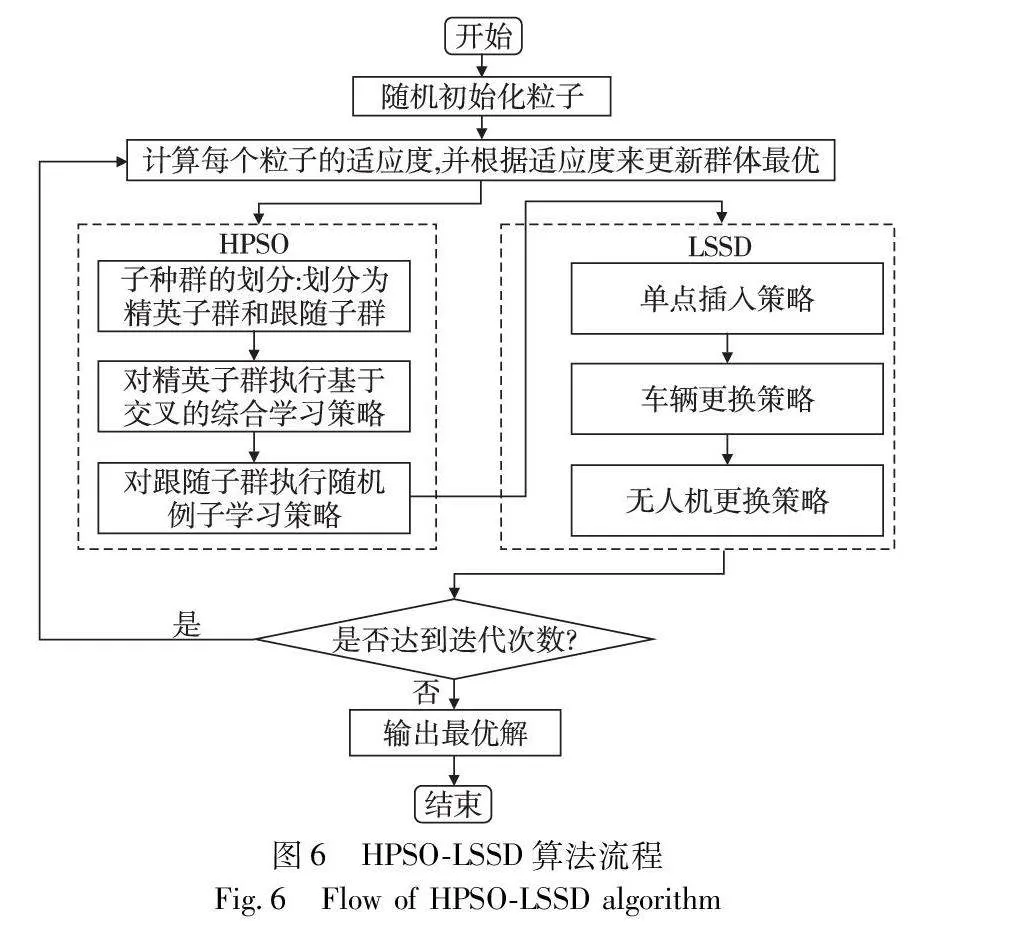
求解VRPDTW问题的HPSO-LSSD算法流程如图6所示。
3 实验与分析
3.1 实验算例及实验环境
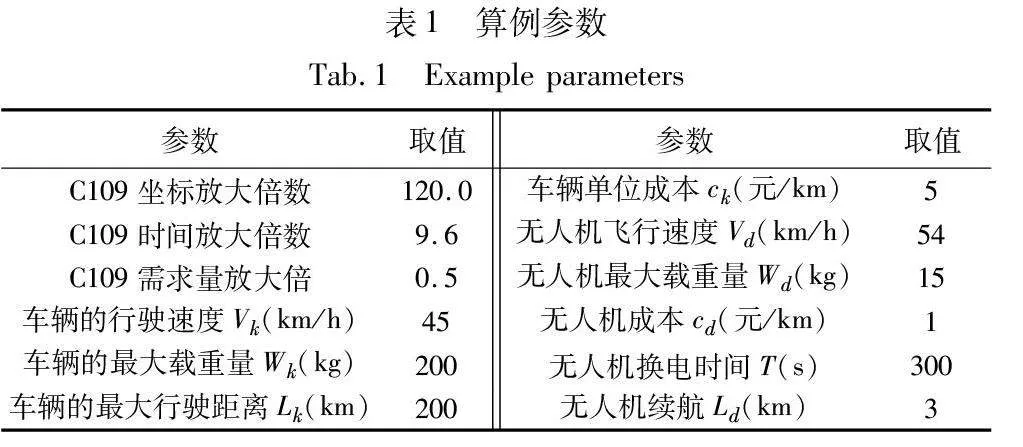
实验数据集采用solomon标准数据集中的C109作为基础算例。为了更符合现实场景数据,本文按比例适当调整了C109的部分数据,并引入车辆以及无人机实际的工作参数,如表1所示。此外,实验的仿真环境是Windows 10,Intel Core i5-11400 CPU@2.60 GHz,16 GB RAM。同时,为了保证算例分析的公平性,每个算法的种群大小都设置为100,迭代次数为200次。每个算法独立运行10次得到实验结果。其中HPSO-LSSD和PSO-LSSD算法的相关参数设置如下:w=0.5,c1=2.0,c2=2.0,λγ=0.5,λc=0.5,λm=0.5。
3.2 算法性能实验
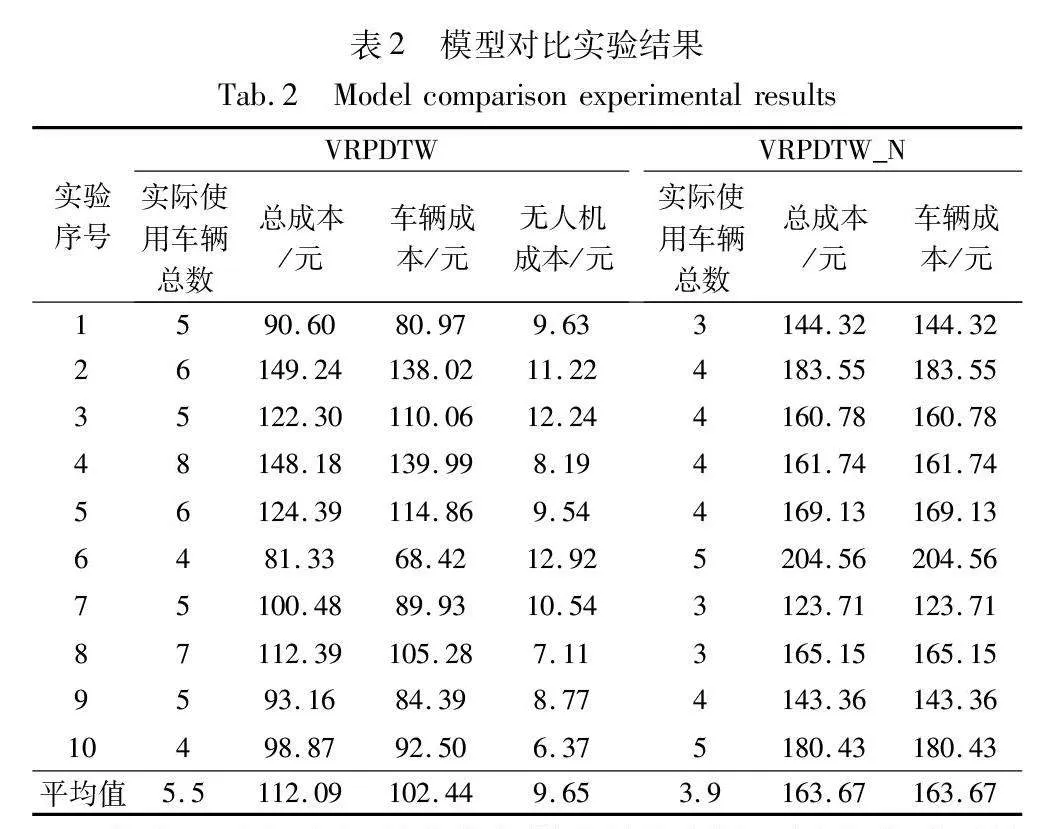
为了验证模型的有效性,本实验假设VRPDTW的所有配送只允许由车辆来完成,其他条件不变,得到一个新模型VRPDTW_N。接着,使用HPSO-LSSD分别求解VRPDTW和VRPDTW_N,实验结果如表2所示。
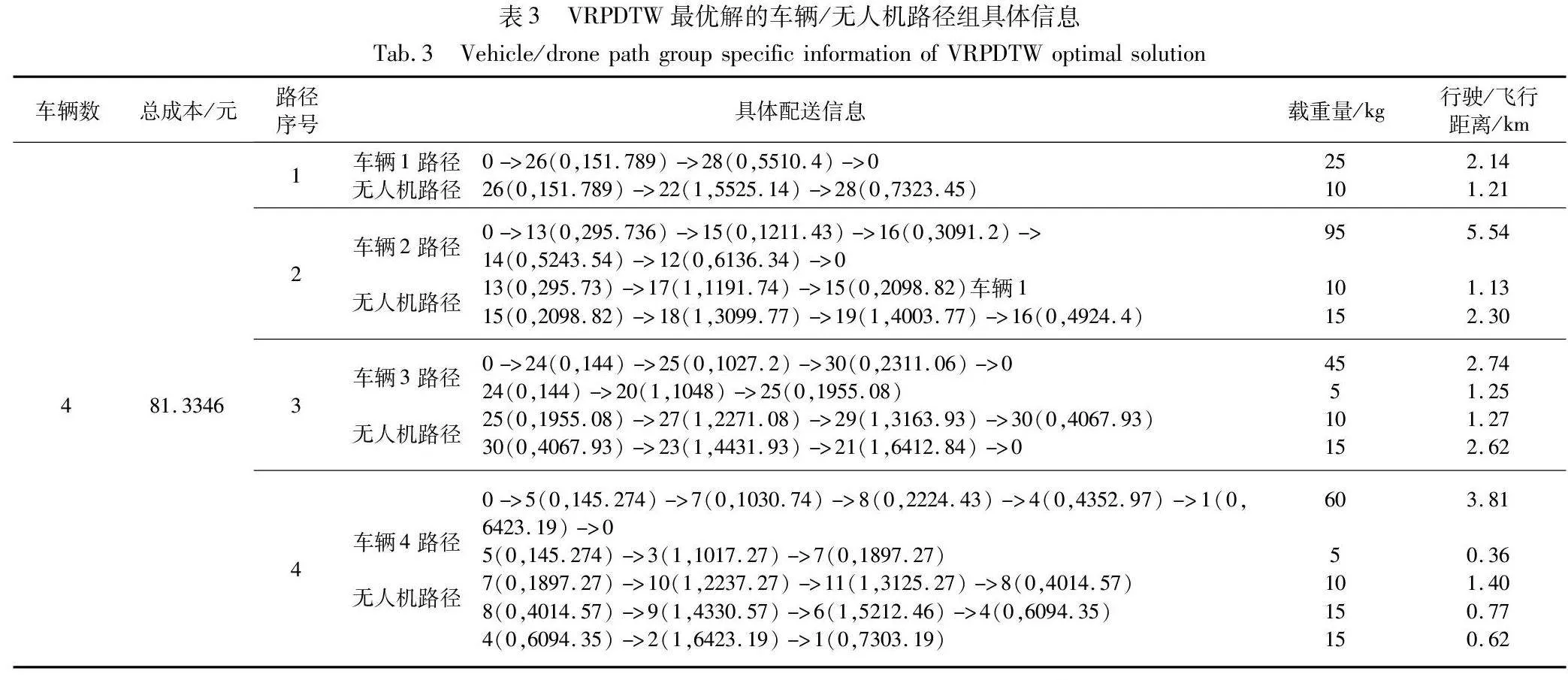
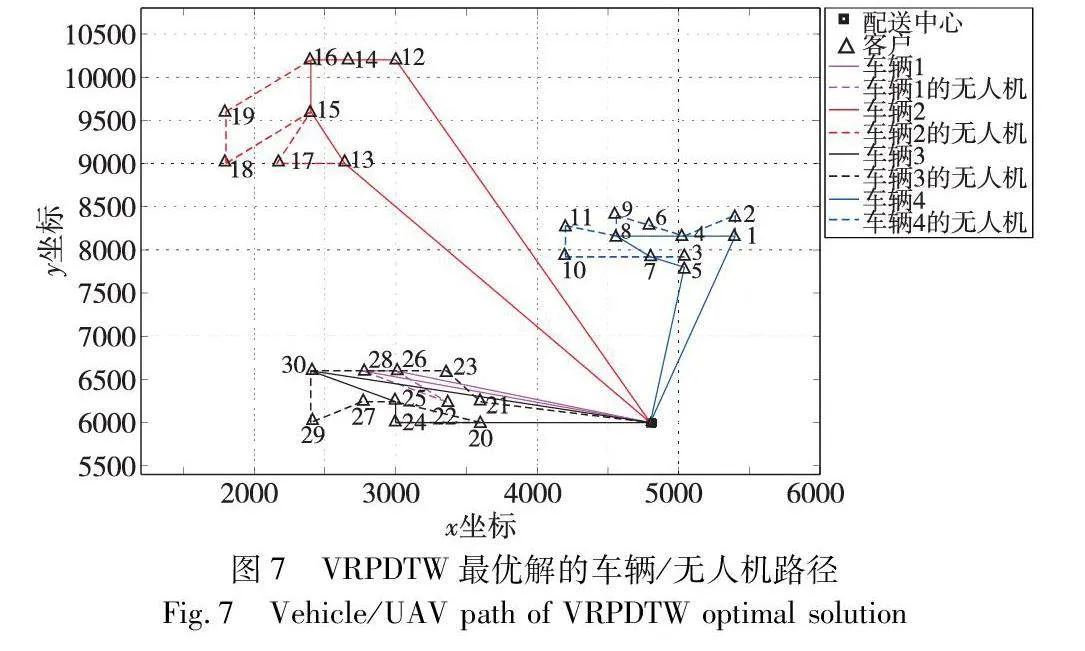
通过表2可以看出,在平均值方面,虽然VRPDTW比VRPDTW_N多使用了9.65元的无人机成本,但VRPDTW的总成本比VRPDTW_N的减少了51.58元,节省了31.51%的成本。由此证明,无人机的加入可以有效提高车辆配送的效率以及降低配送成本。VRPDTW在第6次实验求解得到最优方案,其配送方案如图7所示,而具体的路径信息如表3所示。表3的“具体配送信息”中,每一个节点以Z(Y,X)来表示,Z表示节点序号,Y表示配送工具(0为车辆,1为无人机),X表示车辆/无人机的到达时间(单位:s),节点0的到达时间以0计算。
从表3可以看出,该方案每段路径的车辆/无人机都满足续航约束、载重约束和时间约束。接下来以路径4为例具体分析。路径4的车辆/无人机的行驶/飞行里程分别为3.81 km、0.36 km、1.40 km、0.77 km和0.62 km,符合式(3)和(5)的约束。路径4的车辆实际载重为60+5+10+15+15=105 kg,小于车辆最大载重量。同时,无人机的单次航程载重分别为5 kg、10 kg、15 kg和15 kg,也小于无人机的最大载重量。其中,路径4的无人机在1次飞行中连续服务2个客户,证明模型成功应用到了方案中。此外,路径4中每个客户有且只有一台车辆/无人机提供服务,也满足配送过程中的时间窗约束。由此可见,HPSO-LSSD能有效地求解VRPDTW。
3.3 算法对比实验
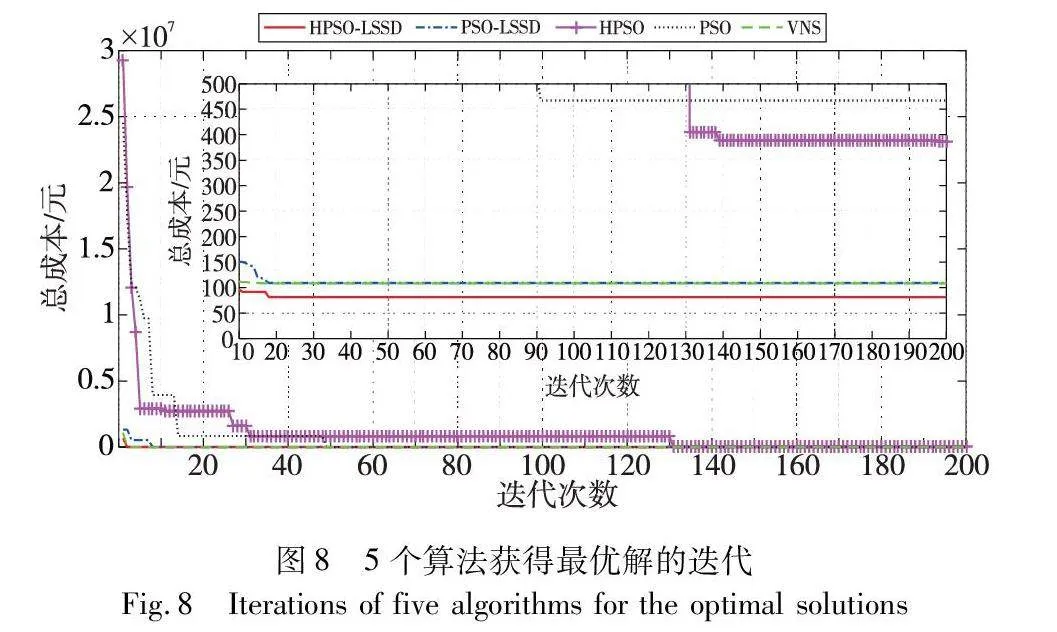
为了验证本文算法的寻优性能,本实验采用四个算法来求解VRPDTW配送模型,所得的实验结果与HPSO-LSSD作对比。其中,第1个算法是传统PSO;第2个对比算法是HPSO;第3个对比算法是PSO-LSSD,即传统PSO加上本文所提出的LSSD;第四个算法是变邻域搜索算法(variable neighborhood search,VNS)[18]。5个算法获得最优解的迭代过程如图8所示。
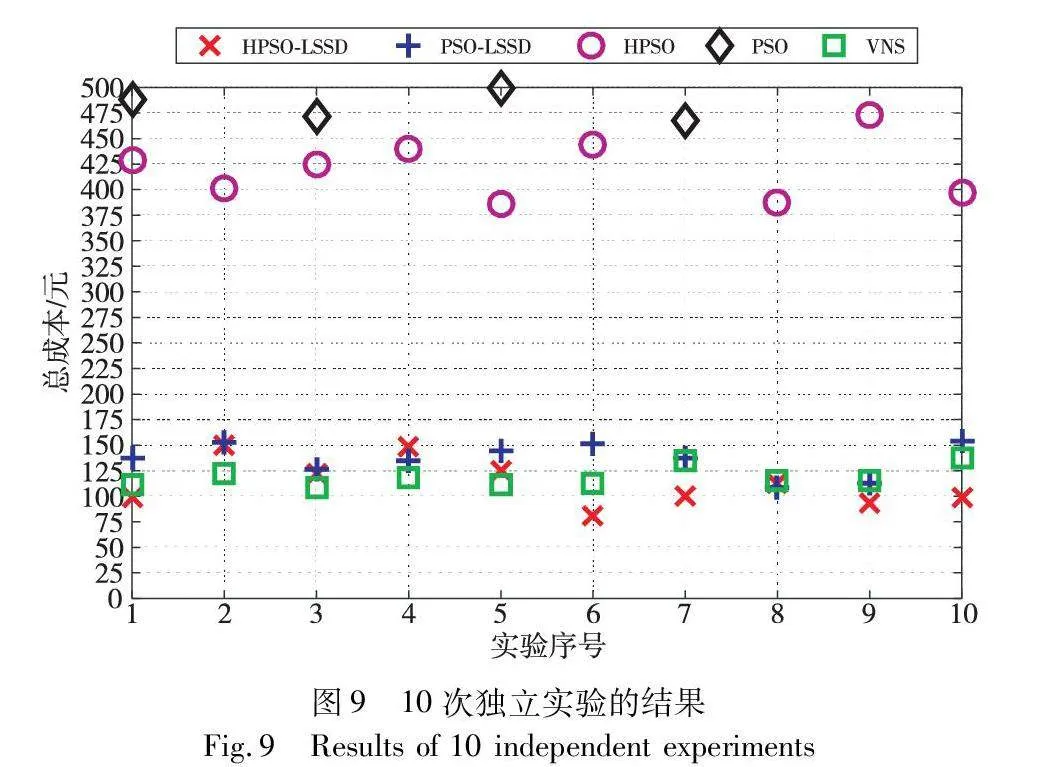
由图8可以看出,HPSO-LSSD和PSO-LSSD、VNS在迭代20次前便收敛到最优值,其收敛速度和效果明显优于HSPO和PSO。10次独立实验的结果如图9所示。
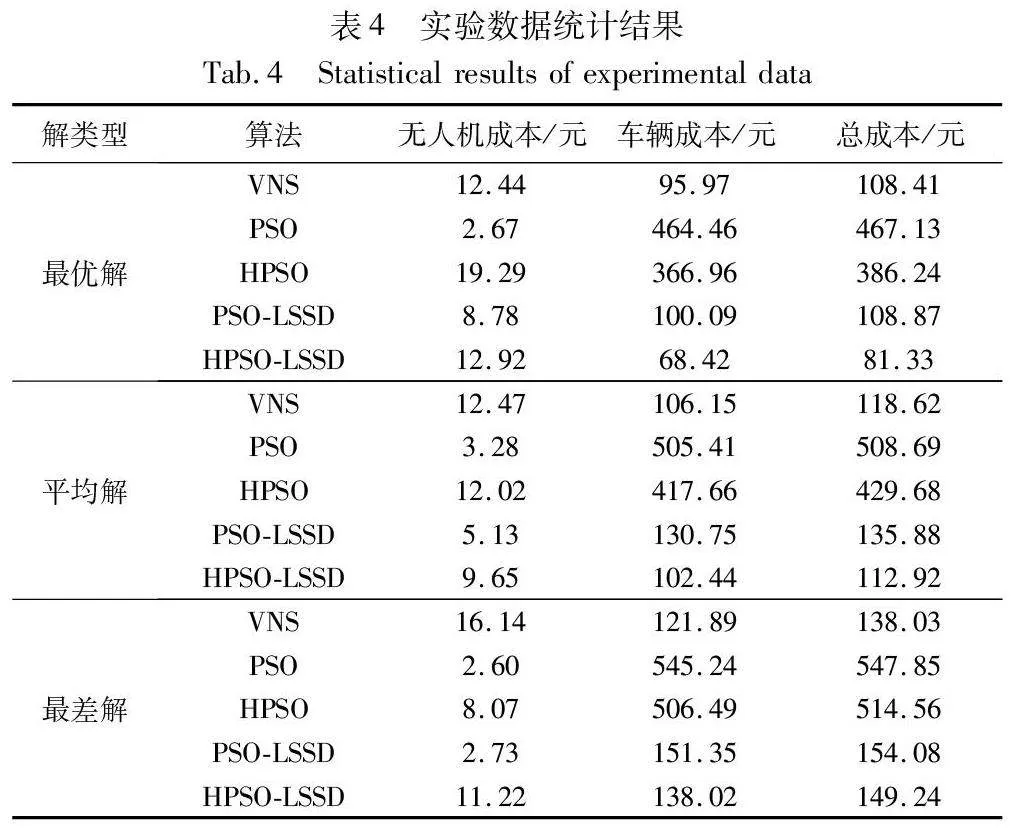
在图9中,HPSO-LSSD和PSO-LSSD、VNS所获得的方案成本在75~175元,而HPSO和PSO所获取的方案成本在375~500元。由此可见,HPSO-LSSD和PSO-LSSD、VNS的求解稳定性明显高于HPSO和PSO。具体的实验数据如表FKlkjDq++VuZh+GEca0Efghs3k6NLBlRWiGiLed6Iqk=4所示。
从表4可以看出,无论是最优解、平均解或者最差解,HPSO-LSSD均优于其他四种算法。HPSO-LSSD所得最优解的总成本分别比PSO-LSSD、HPSO、PSO、VNS节约了27.54元、304.91元、385.80、27.08元,优化率分别达到25.30%、78.94%、82.59%、24.98%。此外,HPSO-LSSD的平均解比HPSO的平均解节约了316.76元,优化率为73.72%;PSO-LSSD的平均解比PSO的平均解节约了395.77元,优化率为77.80%。这证明了本文所提的局部搜索算法能有效提高算法的局部寻优能力。
4 结束语
针对车辆与无人机协同配送问题,本文进一步考虑时间窗、无人机换电以及无人机多点连续配送等因素,提出了VRPDTW,并设计了HPSO-LSSD进行求解。为验证VRPDTW以及HPSO-LSS的有效性,本文对solomon标准数据集中的C109算例进行改造,设计了实验算例。实验结果表明:本文提出的VRPDTW的配送成本远远低于只采用车辆进行配送的VRPDTW_N,节省了31.51%的成本;本文算法优化策略高效可靠,HPSO-LSSD寻优能力远优于PSO-LSSD、HPSO、PSO、VNS,优化率分别为25.71%、70.61%、82.08%、24.98%。
参考文献:
[1]刘正元, 王清华. 无人机和车辆协同配送映射模式综述与展望[J]. 系统工程与电子技术, 2023, 45(3): 785-796. (Liu Zhengyuan, Wang Qinghua. Review and prospect of UAV and vehicle collaborative distribution mapping mode[J]. System Engineering and Electronic Technology, 2023, 45(3): 785-796.)
[2]任璇, 黄辉, 于少伟, 等. 车辆与无人机组合配送研究综述[J]. 控制与决策, 2021, 36(10): 2313-2327. (Ren Xuan, Huang Hui, Yu Shaowei, et al. Summary of research on vehicle and UAV combined distribution[J]. Control and Decision-Making, 2021, 36(10): 2313-2327.)
[3]雷定猷, 宋文杰, 张英贵. 平衡装载约束下的车辆路径问题研究[J]. 计算机应用研究, 2020, 37(6): 1622-1625,1641. (Lei Dingyou, Song Wenjie, Zhang Yinggui. Research on vehicle routing problem under balanced loading constraints[J]. Application Research of Computers, 2020, 37(6): 1622-1625,1641.)
[4]Wang Xingyin, Poikonen S, Golden B. The vehicle routing problem with drones: several worst-case results[J]. Optimization Letters, 2017, 11: 679-697.
[5]Murray C C, Chu A G. The flying sidekick traveling salesman problem: optimization of drone-assisted parcel delivery[J]. Transportation Research Part C: Emerging Technologies, 2015, 54: 86-109.
[6]Ha Q M, Deville Y, Pham Q D, et al. On the min-cost traveling salesman problem with drone[J]. Transportation Research Part C: Emerging Technologies, 2018, 86: 597-621.
[7]王新, 王征, 徐伟. 面向多个无人机站点的车辆与无人机联合配送路径问题研究[J]. 运筹与管理, 2021, 30(5): 31-37. (Wang Xin, Wang Zheng, Xu Wei. Research on vehicle and UAV joint distribution routing problem for multiple UAV sites[J]. Operation and Management, 2021, 30(5): 31-37.)
[8]李妍峰, 李佳, 向婷. 需求可拆分的无人机与卡车协同路径优化问题[J]. 工业工程, 2022, 25(1): 54-63,143. (Li Yanfeng, Li Jia, Xiang Ting. Cooperative path optimization problem of UAV and truck with split demand[J]. Industrial Engineering, 2022, 25(1): 54-63,143.)
[9]Raeesi R, Zografos K G. The electric vehicle routing problem with time windows and synchronised mobile battery swapping[J]. Transportation Research Part B: Methodological, 2020, 140: 101-129.
[10]颜瑞, 陈立双, 朱晓宁, 等. 考虑区域限制的卡车搭载无人机车辆路径问题研究[J]. 中国管理科学, 2022, 30(5): 144-155. (Yan Rui, Chen Lishuang, Zhu Xiaoning, et al. Research on vehicle routing problem of truck with UAV considering regional constraints[J]. China Management Science, 2022, 30(5): 144-155.)
[11]范厚明, 张跃光, 田攀俊. 时变路网下多中心电动车-无人机协同配送路径优化[J]. 管理工程学报, 2023, 37(2): 131-142. (Fan Houming, Zhang Yueguang, Tian Panjun. Multi-center electric vehicle-UAV cooperative distribution path optimization under time-varying road network[J]. Chinese Journal of Industrial Enginee-ring and Engineering Management, 2023, 37(2): 131-142.)
[12]Huang S H, Huang Y H, Blazquez C A, et al. Solving the vehicle routing problem with drone for delivery services using an ant colony optimization algorithm[J]. Advanced Engineering Informatics, 2022, 51: 101536.
[13]Di Puglia Pugliese L, Guerriero F. Last-mile deliveries by using drones and classical vehicles[C]//Proc of Optimization and Decision Science: Methodologies and Applications.Cham:Springer, 2017: 557-565.
[14]戚远航, 蔡延光, 蔡颢, 等. 带容量约束的供应链物流运输调度问题的双层变邻域蝙蝠算法[J]. 电子学报, 2019,47(7): 1434-1442. (Qi Yuanhang, Cai Yanguang, Cai Hao, et al. Two-layer variable neighborhood bat algorithm for supply chain logistics transportation scheduling problem with capacity constraints[J]. Journal of Electronics, 2019, 47(7): 1434-1442.)
[15]Liang Baoxian, Zhao Yunlong, Li Yang. A hybrid particle swarm optimization with crisscross learning strategy[J]. Engineering Applications of Artificial Intelligence, 2021, 105: 104418.
[16]张硕, 钱晓明, 楼佩煌, 等. 基于改进粒子群算法的大规模自动导引车系统路径规划优化[J]. 计算机集成制造系统, 2020, 26(9): 2484-2496. (Zhang Shuo, Qian Xiaoming, Lou Peihuang, et al. Path planning optimization of large-scale automatic guided vehicle system based on improved particle swarm optimization[J]. Computer Integrated Manufacturing System, 2020, 26(9): 2484-2496.)
[17]马俊, 张纪会, 郭乙运. 考虑客户分类的随机时间车辆路径优化模型与算法[J]. 计算机应用研究, 2022, 39(7): 1979-1984. (Ma Jun, Zhang Jihui, Guo Yiyun. Random time vehicle routing optimization model and algorithm considering customer classification[J]. Application Research of Computers, 2022, 39(7): 1979-1984.)
[18]Qi Yuanhang, Cai Yanguang. Hybrid chaotic discrete bat algorithm with variable neighborhood search for vehicle routing problem in complex supply chain[J]. Applied Sciences-Basel, 2021, 11(21): 10101.

