自动控制系统稳定性教学中的思政元素设计

摘 要：针对传统自动控制原理课程教学的不足，将某型号转子绕线机控制系统引入系统稳定性案例教学课堂。通过对案例的数学建模，分别应用时域分析法中的劳斯判据、赫尔维茨稳定判据，系统输出曲线和频域分析法中的奈奎斯特稳定判据及对数稳定判据分析控制系统的稳定性。课程将思政元素与系统稳定性知识有机融合，引申出“条条大路通罗马”的问题解决思想和引导学生认识社会系统稳定的重要意义及自身责任。

关键词：自动控制原理；案例教学；时域分析法；频域分析法；思政元素

中图分类号：G641 文献标志码：A 文章编号：2096-000X（2024）23-0067-04

Abstract： In view of the shortcomings of the traditional Automatic Control Principle course teaching， the control system of a certain type of rotor winding machine is introduced into the system stability case teaching class. Through the mathematical modeling of the case， the stability of the control system is analyzed by applying the Routh criterion， Herwitz stability criterion and system output curve in the time domain analysis method， and the Nyquist stability criterion and logarithmic stability criterion in the frequency domain analysis method. The course organically integrates ideological and political elements with knowledge of system stability， extends the problem-solving idea of "all roads lead to Rome"， and guides students to understand the importance of social system stability and their own responsibilities.

Keywords： Automatic Control Principle; case teaching; time domain analysis method; frequency domain analysis method; ideological and political elements

自动控制原理课程内容繁多，知识理论性强且抽象，不易理解，是一门具有一定难度和深度的专业基础课程，要求学生具有扎实的专业功底和较强的抽象思维能力[1]。系统稳定性作为自动控制原理课程的核心内容，在系统稳定性判别方法讲授过程中引入某型号转子绕线机控制系统实际案例，使学生容易分析理解，有利于后续的自动控制原理课程的学习与知识的实际应用[2]。利用Matlab软件进行控制系统传递函数编程，分析系统稳定性，培养学生利用计算机解决实际问题的能力。课程将思政元素与系统稳定性有机融合，在传授知识的同时，培养学生个人素养和爱国主义情怀[3]。

一 传统教学特点

在自动控制原理课程的传统教学中，课程内容包括数学建模、时域分析、根轨迹法、频域分析、系统综合与校正、非线性系统分析和离散系统分析等[4]。在教学过程中存在如下四个方面的问题。

第一，教学大纲内容陈旧，无法顺应时代需求。传统教学中，较少将知识点与实际的问题关联，缺少自动控制领域的新动态、新成果、新经验和新问题的介绍[5]。

第二，教学手段匮乏，课堂效果较差。教学中涉及大量的公式推导、响应分析等，学生将大部分课堂时间用于记笔记，较少与教师交流讨论，课堂上对知识的理解较差，容易使学生失去学习兴趣。

第三，实践环节薄弱，实验内容较少。传统实践教学环节投入不足，学生只能进行特定实验，操作能力与创新能力得不到很好的锻炼，难以调动学习积极性[6]。

第四，思政元素不够重视，引入较少。教师只注重理论知识的传输，忽略了对学生的思想政治教育。将思政元素与教学知识相结合，培养学生的思政品质，也是课程教学的重要内容[7]。

为改善上述问题，将具体实际案例引入系统稳定性教学课堂，并融入思政元素，充分发挥学生个人主观能动性，使知识内容具体化，易于理解，可培养学生正确的价值观。

二 案例教学的设计

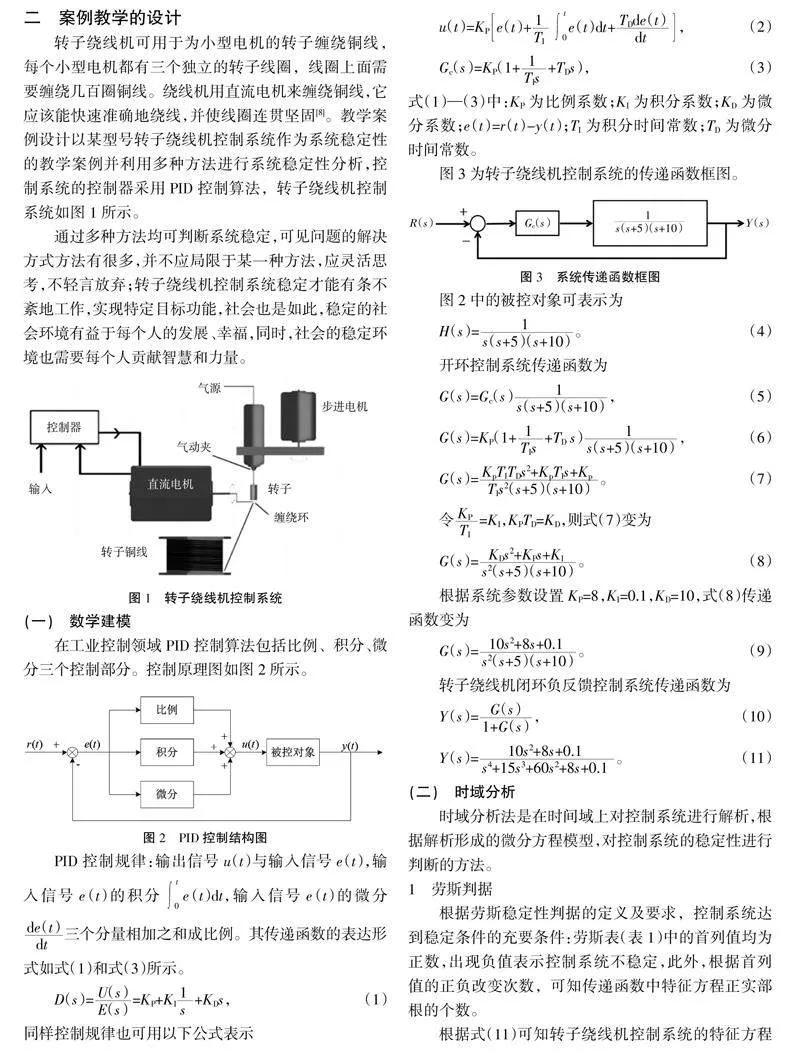
转子绕线机可用于为小型电机的转子缠绕铜线，每个小型电机都有三个独立的转子线圈，线圈上面需要缠绕几百圈铜线。绕线机用直流电机来缠绕铜线，它应该能快速准确地绕线，并使线圈连贯坚固[8]。教学案例设计以某型号转子绕线机控制系统作为系统稳定性的教学案例并利用多种方法进行系统稳定性分析，控制系统的控制器采用PID控制算法，转子绕线机控制系统如图1所示。

通过多种方法均可判断系统稳定，可见问题的解决方式方法有很多，并不应局限于某一种方法，应灵活思考，不轻言放弃；转子绕线机控制系统稳定才能有条不紊地工作，实现特定目标功能，社会也是如此，稳定的社会环境有益于每个人的发展、幸福，同时，社会的稳定环境也需要每个人贡献智慧和力量。

（一） 数学建模

在工业控制领域PID控制算法包括比例、积分、微分三个控制部分。控制原理图如图2所示。

（二） 时域分析

时域分析法是在时间域上对控制系统进行解析，根据解析形成的微分方程模型，对控制系统的稳定性进行判断的方法。

1 劳斯判据

根据劳斯稳定性判据的定义及要求，控制系统达到稳定条件的充要条件：劳斯表（表1）中的首列值均为正数，出现负值表示控制系统不稳定，此外，根据首列值的正负改变次数，可知传递函数中特征方程正实部根的个数。

根据式（11）可知转子绕线机控制系统的特征方程为s4+15s3+60s2+8s+0.1=0，利用劳斯判据判断系统稳定性。首先列写劳斯表见表2。

由表2可知，第一列值全为正，故该系统稳定。

2 赫尔维茨稳定判据和系统输出曲线

赫尔维茨稳定判据判断线性系统稳定的必要条件是：特征方程的各项系统为正数。

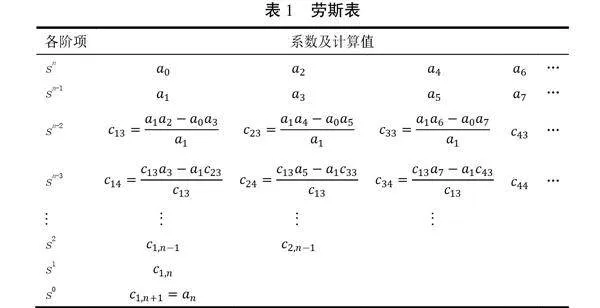
根据式（11）利用Matlab绘制系统传递函数输出响应曲线，曲线如图4所示。

根据式（10）分母特征方程和赫尔维茨稳定判据可知转子绕线机控制系统稳定。根据图4输出响应曲线也可以看出系统输出稳定，稳定值为1。

（三） 频域分析

频域分析法是以系统输入不同正弦函数信号的频率作为自变量，通过建立信号稳态输入与输出关联的数学模型，研究输出与输入之间存在的关系，以此模型来分析控制系统具体状态。

1 奈奎斯特稳定判据

利用反馈调节的控制系统，判断其稳定充分必要条件：当闭环控制系统的开环传递函数G（s）H（s）在s平面中的原点和虚轴上不存在极点时，ω由-∞→+∞变化，控制系统开环幅相频率特性曲线围绕（-1，j0）点，半闭合特性曲线穿越负实轴点（-1，j0）的左侧次数记为N，控制系统的开环传递函数在s平面右半部分的极点个数记为P，当2N=P，可判定闭环控制系统是稳定的，否则为不稳定系统。当闭环控制控制系统的开环控制系统稳定，即系统的开环传递函数G（s）H（s）的极点均在s平面左半部分，即P=0，则此闭环控制系统能够判断为稳定系统的充分必要条件为绘制出的奈氏曲线不包围（-1，j0）点。

根据转子绕线机控制系统的闭环传递函数式（11），利用Matlab绘制奈氏曲线图如图5所示。

由图5可知，转子绕线机控制系统的闭环传递函数绘制的奈氏图未包围（-1，j0）点，且根据式（9）可知其系统的开环传递函数特征方程的系数均为正，因此开环控制系统是稳定的，综上可知，转子绕线机闭环控制系统是稳定的。

2 对数稳定判据

对数稳定判据实质上是奈奎斯特稳定判据的延伸，在控制系统的对数幅频特性曲线L（ω）>0 dB的范围内，控制系统的开环对数相频特性曲线正、负穿越（2k+1）π，（k=0，1，2，3…）次数之差为P/2，即N=N+-N-=P/2，可判断为控制系统是稳定的。其中，N+表示正穿越的次数总和，N-表示负穿越的次数总和。

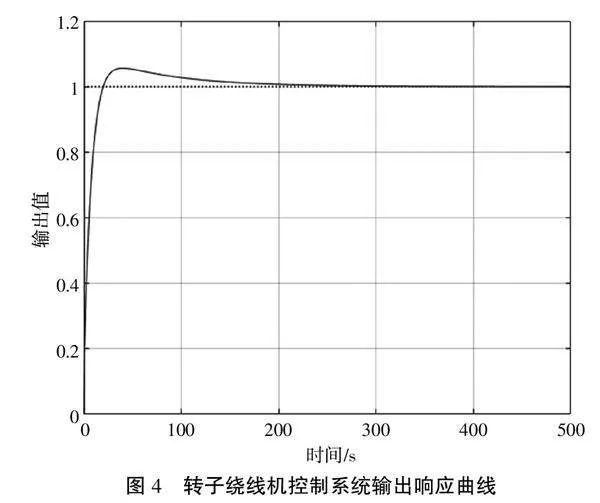
根据转子绕线机控制系统的闭环传递函数式（11），利用Matlab绘制伯德图如图6所示。

据图6可知， 在L（ω）>0频段内，相频曲线与-180°线无交点，故N=N+-N-=0。幅值裕度h=inf，相角裕度γ=160°，根据式（9）很容易知道开环系统是稳定的，因此，极点个数P=0。综上条件可知h=inf>0，γ=160°>0，且N=P/2=0，可判断转子绕线机控制系统非常稳定。

三 思政元素的融合

通过对教学案例系统稳定性知识点理解和分析，总结出思政元素融合点如下。

首先，从系统稳定性的多种判断方法可以看出，解决某一问题或处理某一事情的方法和途径有很多。虽然各不相同、各有差异，但是最终的结果是一致的，真实体现出“条条大路通罗马”这句谚语的真谛。同时也告诉青年大学生无论是在生活、学习还是工作中，当一种途径已经确认无法达到想要的结果时，不应自暴自弃、轻言放弃，应保持思维敏捷，换种方式方法进行实施或思考也许会得到意想不到的效果。

其次，通过对转子绕线机控制系统稳定的重要性进行分析，充分引导青年大学生认识社会稳定发展的重要意义及自身肩负的社会责任。系统稳定是控制系统能够运行的首要条件，不论是时域法还是频域法，都要对稳定性作出判定。只有系统是稳定的，才能实现预定的控制任务。对于社会这个大系统也是一样，只有稳定的社会环境，国家才能建设得更好[9]。大学生更应成为维护社会稳定的重要力量，小到宿舍、班级、家庭的稳定，大到学校、社会、国家的稳定，为实现国家发展作出应有的贡献。

四 结束语

案例教学设计通过转子绕线机控制系统的数学建模过程、不同时域方法和不同频域方法分析系统稳定性过程，使学生能够充分理解和掌握稳定性判据知识内容。在分析转子绕线机控制系统稳定性过程中利用Matlab软件绘制图形，使解决问题的过程更加容易，直观易懂，培养学生的编程能力和解决实际问题的能力，将学习的理论知识点向实际转化。同时，课程在案例设计过程中将知识点与思政元素有机融合，总结出“条条大路通罗马”和通过系统稳定性映射社会稳定意义的主要思政点，构造学生正确的社会主义核心价值观，提升个人素养，为社会稳定和国家发展贡献力量。

参考文献：

[1] 肖敏，林金星，王晓玲.基于案例教学法的“自动控制原理”课程教学[J].教育教学论坛，2021（30）：140-143.

[2] 薛鹏，程辉，郭会平.自控原理课程的“一例到底”教学设计[J].科技风，2020（20）：33，41.

[3] 朱文兴.“自动控制原理”课程思政教学案例设计与实践[J].电气电子教学学报，2021（5）：16-19.

[4] 胡寿松.自动控制原理[M].北京：科学出版社，2019.

[5] 杨裕翠.“自动控制原理”课程的教学改革[J].教育现代化，2019（5）：70-72.

[6] 杨秦敏，陈积明，曹伟伟，等.课程教学与实际案例相融合的研究与实践——以“自动控制原理”课程为例[J].工业和信息化教育，2020（3）：29-34.

[7] 鱼轮，李亚文.立德树人背景下“自动控制原理”课程思政探索[J].工业和信息化教育，2022（8）：60-63.

[8] 季丽丽，马骥.基于MATLAB转子绕线机控制系统调节器的仿真研究[J].沈阳大学学报（自然科学版），2012（1）：25-27.

[9] 王立红.自动控制理论课程思政建设探索[J].轻工科技，2021（10）：133-134.

基金项目：2022年度辽宁省普通高等教育本科教学改革研究一般项目“面向数字化需求的材料成型及控制工程专业创新型人才培养改革与实践”（无编号）、“基于产教融合、协同育人的金属材料工程专业应用型人才培养模式创新研究与实践”（无编号）

第一作者简介：孙杰（1984-），男，汉族，山东菏泽人，工学博士，教授，博士研究生导师。研究方向为板带轧制智能化控制关键技术和连轧自动化控制系统研发。