基于可学习攻击步长的联合对抗训练方法

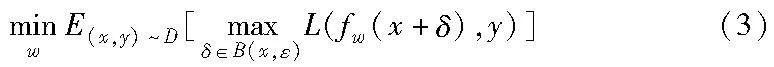
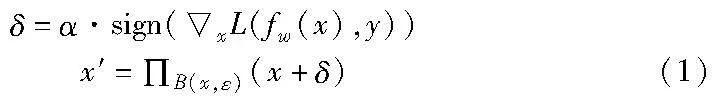
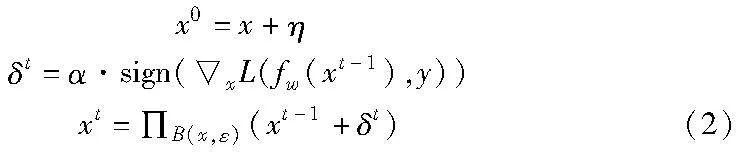
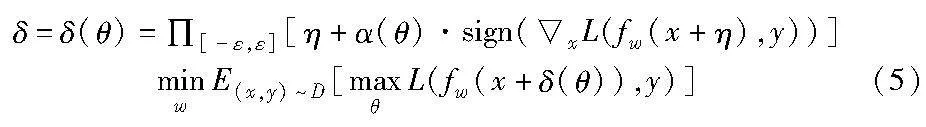
摘 要：对抗训练（AT）是抵御对抗攻击的有力手段。然而，现有方法在训练效率和对抗鲁棒性之间往往难以平衡。部分方法提高训练效率但降低对抗鲁棒性，而其他方法则相反。为了找到最佳平衡点，提出了一种基于可学习攻击步长的联合对抗训练方法（FGSM-LASS）。该方法包括预测模型和目标模型，其中，预测模型为每个样本预测攻击步长，替代FGSM算法的固定大小攻击步长。接着，将目标模型参数和原始样本输入改进的FGSM算法，生成对抗样本。最后，采用联合训练策略，共同训练预测和目标模型。在与最新五种方法比较时，FGSM-LASS在速度上比鲁棒性最优的LAS-AT快6倍，而鲁棒性仅下降1%；与速度相近的ATAS相比，鲁棒性提升3%。实验结果证明，FGSM-LASS在训练速度和对抗鲁棒性之间的权衡表现优于现有方法。

关键词：对抗训练； 对抗样本； 对抗攻击； 预测模型； 可学习攻击步长

中图分类号：TP391.41 文献标志码：A

文章编号：1001-3695（2024）06-036-1845-06

doi：10.19734/j.issn.1001-3695.2023.09.0431

Joint adversarial training method based on learnable attack step size

Abstract：AT is a powerful means to defend against adversarial attacks. However， currently available methods often struggle to strike a balance between training efficiency and adversarial robustness. Some methods increase training efficiency but decrease adversarial robustness， while others do the opposite. To achieve the best trade-off， this paper proposed a joint adversa-rial training method based on a learnable attack step size（FGSM-LASS） . This method included a prediction model and a target model. The prediction model predicted an attack step size for each example， which replaced the fixed-size attack step size using in the FGSM algorithm. Subsequently， the improved FGSM algorithm feeded both the target model parameters and original examples to generate adversarial examples. Finally， the prediction model and the target model perform joint adversarial training using these adversarial examples. Compared to the five most recent methods， FGSM-LASS was six times faster than LAS-AT， which was the best performing method in terms of robustness， with only 1% decrease in robustness. It was 3% more robust than ATAS， which was comparable in speed. Extensive experimental results fully demonstrate that FGSM-LASS outperforms current methods in the trade-off between training speed and adversarial robustness.

Key words：adversarial training（AT）; adversarial example; adversarial attack; prediction model; learnable attack step size

0 引言

近年来，随着GPU计算能力的飞速提升，深度学习模型在图像分类［1，2］、目标检测［3］、语义分割［4］、语音识别等领域取得了显著成功。然而，Szegedy等人［5］揭示了深度学习模型中对抗样本的存在，这使得模型在面对对抗样本攻击时显得异常脆弱。为了解决对抗样本对深度学习模型的攻击，研究者们提出了许多防御方法，其中较为有效且广泛应用的是对抗训练。Goodfellow等人［6］最早提出利用对抗训练（adversarial training，AT）来抵御对抗样本的攻击。他们采用快速梯度符号法（fast gradient sign method，FGSM）生成对抗样本以训练模型，从而增强模型对抗攻击的能力。随后，Madry等人［7］提出使用投影梯度下降法（projected gradient decent，PGD）生成对抗样本进行模型训练。然而，由于PGD算法在生成用于训练的对抗样本时需要进行多次模型前向与反向传播以计算梯度，所以训练速度较慢。虽然与FGSM相比，PGD能够使训练好的模型具有更强的对抗鲁棒性，但由于训练速度过慢，这一方法在实际应用中受到了一定的质疑。相比之下，FGSM在生成对抗样本时只需进行一次前向与反向传播，训练速度较快，但其模型的对抗鲁棒性相对较弱，无法满足应用需求。因此，如何在保证训练效率的同时提高模型的对抗鲁棒性，成为了当前研究的重点。

一些研究致力于对PGD算法进行优化。Cai等人［8］提出了一种课程学习策略，其目的是加速训练过程。在训练初期，采用较低强度的攻击来生成对抗样本。当模型在某一攻击强度下达到较高准确率时，便提高攻击强度。该策略的核心是在训练过程中逐步增加PGD的迭代次数，从而提高攻击强度。随后，Ye等人［9］提出了一种调整迭代次数的策略。该策略设定了最小和最大迭代次数，并在整个训练过程中，从最小迭代次数开始均匀增加迭代次数，直至达到最大迭代次数。前面提到的两种方法都是基于PGD迭代次数进行规律性调整的，虽然这些调整在一定程度上提高了训练速度，但与原始PGD相比，模型的对抗鲁棒性却明显下降。因此，Jia等人［10］提出了一种基于可学习攻击策略的对抗训练方法（AT with learnable attack strategy，LAS-AT），并提出了一种用于预测PGD的攻击策略（包括攻击步长、迭代次数和最大扰动强度）。随着训练的进行，这些策略会根据强化学习进行优化，为后续训练提供更具攻击性的对抗样本，从而提高目标模型的对抗鲁棒性。尽管LAS-AT极大地提高了模型的对抗鲁棒性，但预测的迭代次数仍然较大，且需要强化学习机制来训练策略模型的参数，这两点导致了训练速度极慢，甚至低于原始的PGD训练速度。尽管基于PGD算法的研究能够为模型提供较高的对抗鲁棒性，但训练速度问题限制了其应用。因此，许多研究开始转向对FGSM算法进行分析和改进。

FGSM算法是一种高效生成对抗样本的攻击方法，因其生成过程简洁且速度快，在许多场景中得到了广泛应用。然而，FGSM采用固定大小的攻击步长，导致生成的对抗样本过于单一，缺乏多样性。在训练过程中，模型可能对这些单一的对抗样本产生适应，从而过拟合FGSM攻击生成的对抗样本。这会降低模型对其他攻击算法（如PGD）的对抗鲁棒性，即模型的泛化能力较差。为了提高模型的泛化能力，需要对固定大小的攻击步长进行调整，以产生更多样化的对抗样本，从而提高训练得到模型的泛化能力。

Wong等人［11］对原始样本添加随机初始化（随机步）来提高对抗样本的多样性，从而降低模型过拟合于对抗样本的风险。该方法将原始样本输入 FGSM 算法生成用于训练模型的对抗样本，其中样本经过随机初始化，被称为基于随机初始化的快速梯度符号法对抗训练（FGSM AT with random step，FGSM-RS）。Kim等人［12］对FGSM-RS训练得到的模型进行探究，发现其对较小的对抗扰动的抵御能力较弱，而对较大的对抗扰动有较好的抵御力。他们将这一现象称为决策边界扭曲，并提出一种解决方法：在训练过程中，沿着对抗干扰方向验证内部区间，即调整对抗扰动大小，观察模型的预测结果，以找出最小的能使模型预测出错的对抗扰动下的对抗样本，以此训练模型，以有效防止决策边界扭曲问题，这种方法被称为基于检查点的快速梯度符号法对抗训练（FGSM AT with checkpoint，FGSM-CKPT）。Andriushchenko等人［13］提出了一种基于梯度对齐的快速梯度符号法对抗训练（FGSM AT with gradient alignment，FGSM-GA）。该方法的主要思想是将样本的梯度执行梯度对齐算法，使得生成的对抗样本在梯度空间中更接近原始样本。这样可以增加模型在梯度空间中的稳定性，使模型更难以过拟合于 FGSM 算法生成的对抗样本，从而提高模型的泛化能力。Huang等人［14］则提出了一种自适应攻击步长的对抗训练方法（AT with adaptive step size，ATAS）。该方法通过对每个样本的梯度范数进行动量累积，根据范数值计算攻击步长，对范数较大的样本采用较小的攻击步长，对范数较小的样本采用较大的攻击步长。这样可以使得生成的对抗样本具有较好的多样性，更有利于提高模型的泛化能力和对抗鲁棒性。上述基于 FGSM 扩展的对抗训练方法在训练速度和对抗鲁棒性之间仍存在权衡不足的问题。部分方法在训练效率方面表现良好，但对抗鲁棒性仍不够强，如 FGSM-RS、FGSM-CKPT和ATAS。而 FGSM-GA 虽然在提高对抗鲁棒性方面表现出色，但使用梯度对齐算法来增加对抗样本的多样性会导致训练成本上升，从而降低训练速度。

本文提出了一种基于可学习攻击步长的联合对抗训练方法（FGSM AT with learnable attack step size，FGSM-LASS）。该方法使用一个预测模型为每个原始样本预测一个攻击步长，并将其应用于FGSM来生成对抗样本。预测模型和目标模型使用这些生成的对抗样本进行联合训练。在该方法中，每个原始样本预测的攻击步长会随着预测模型的训练而得到不断的学习，攻击步长的学习能力有助于持续为目标模型提供更加多样的对抗样本，为后续的训练持续提供有效的攻击，极大程度地降低了目标模型对对抗样本的过拟合风险，从而提高目标模型的泛化能力和对抗鲁棒性。通过与上述对抗训练方法的实验对比发现，本文方法在训练速度上具有优势，同时还能有效提升目标模型的对抗鲁棒性。

1 预备知识

1.1 对抗攻击

文献［6］提出了FGSM。该方法将原始样本x输入模型进行前向传播，得到的结果与类别标签y计算模型损失，然后对损失进行反向传播，得到原始样本的梯度，将梯度符号与攻击步长α相乘得到对抗扰动δ，继而得到对抗样本，公式如下：

其中：ε 为扰动预算；Π B（x，ε） （x+δ）表示将x+δ限制在以x为中心ε为半径的区域内，也就是将对抗样本x′限制在扰动预算 ε 范围内；f w表示参数为w的目标模型；L表示损失函数，x表示求x的梯度；sign为取符号函数。PGD算法［7］在FGSM的基础上进行了扩展，FGSM进行一次前向与反向传播，而PGD采用多次前向与反向传播，即多次迭代FGSM算法，但采用了更小的攻击步长α，公式如下：

其中：t为迭代次数；η为随机初始化扰动；x0为x随机初始化后的样本，作为PGD算法的初始输入；δt 为第t次迭代计算得到的对抗扰动；xt-i表示t-1次迭代计算得到的对抗样本，作为第t次迭代计算的输入，有关符号在式（1）中已有解释，此处不再赘述。根据迭代次数的不同，PDG可分为PGD-10、PGD-20和PGD-50。Wang等人［15］提出根据动量积累方差来调整原始样本的梯度，以提高对抗攻击的可迁移性。

除了上述基于梯度的对抗攻击方法外，Carlini等人［16］提出了一种基于优化的对抗攻击方法。这种方法通过优化扰动后的样本，使其与原始样本的距离最小，被称为C&W（carlini and wagner attack）。Croce等人［17］则提出了一种自动化的攻击手段，采用几种无参数攻击的有序集合来自动化攻击目标模型，这种方法被称为自动攻击（auto attack，AA）。

1.2 对抗训练

对抗训练可以被形式化为一个最大最小优化问题，将对抗攻击生成的对抗样本输入到目标模型计算损失，作为对抗训练的内部最大化损失，然后使用该损失利用梯度下降算法更新目标模型的参数，找到一个既能在原始干净样本上表现良好，又能在对抗样本上具有较高对抗鲁棒性的模型参数。公式如下：

其中：x表示数据集D中的原始干净样本；y为x的类别标签；ε为扰动预算；δ为对抗扰动，δ∈B（x，ε）表示δ被限制在以x为中心ε为半径的圆形区域内；fw表示参数为w的深度学习模型；L表示损失函数。

2 本文方法

本文提出了一种涉及预测模型和目标模型两个模型的方法。目标模型为一个图像分类深度学习模型，是训练的目标，用fw表示，其中w是模型参数。预测模型为一个简单的自定义模型，用于辅助目标模型的训练，后续将详细介绍预测模型的结构。预测模型旨在预测各个样本所对应的攻击步长。根据预测的攻击步长，采用FGSM算法生成对抗样本，并将这些生成的对抗样本用于训练预测和目标模型。

预测模型的目标是通过联合对抗训练动态学习原始样本对应的攻击步长，以增加生成的对抗样本的多样性。这旨在为目标模型持续提供有效的攻击，防止目标模型对对抗样本产生适应性而导致过拟合。这种方法可以有效地提高目标模型的对抗鲁棒性，确保目标模型在面临各种对抗性攻击时仍具有较高的性能。

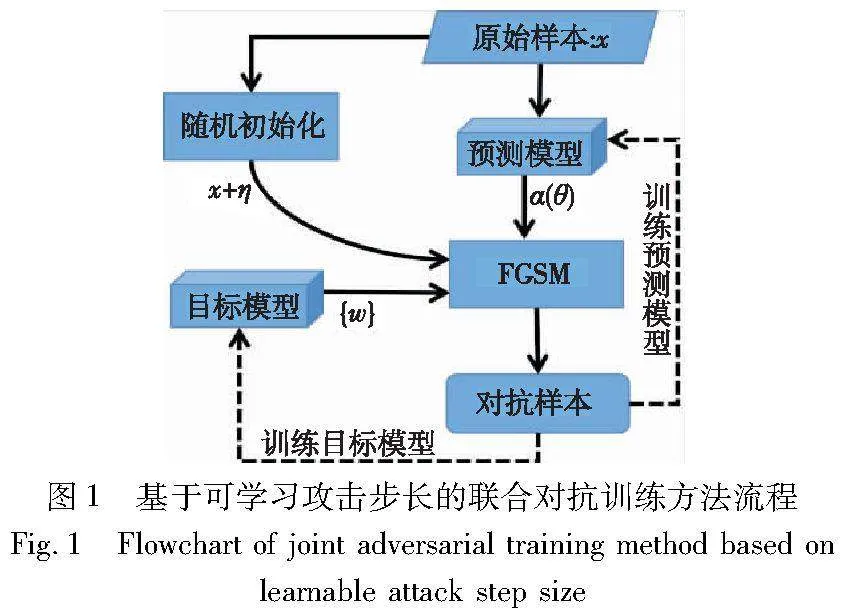
本文方法的整体流程如图1所示。实线部分展示了对抗样本的生成过程，而虚线部分描述了预测模型和目标模型的联合训练过程。

2.1 预测模型架构

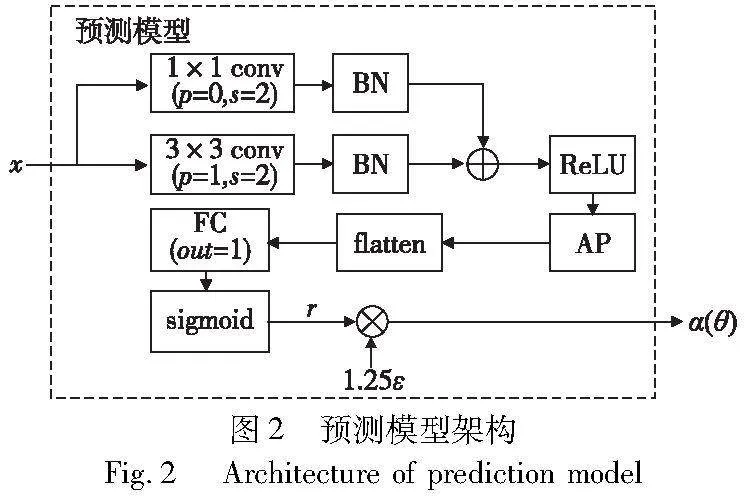
图2展示了预测模型的整体结构，该模型包括一个残差块、ReLU激活层［18］、平均池化层（AP）、flatten层、全连接层（FC）和sigmoid激活层。残差块由一个3×3卷积层（conv）、两个批量归一化层（BN）和一个1×1卷积层构成。

在预测模型中，原始样本经过残差块进行特征提取后，依次经过ReLU激活层、AP、flatten层、FC和sigmoid激活层，最终得到一个比例值r。这个比例值r用于控制攻击的强度，其取值范围为0～1。为了确定攻击步长，将r乘以1.25ε（ε为扰动预算，通常设为8/255），就可以得到对应的攻击步长，用于对原始样本进行攻击，使其在一定程度上偏离原始样本，从而得到需要的对抗样本。攻击步长计算公式定义如下：

r=PMθ（x），α=α（θ）=1.25εr（4）

其中：x为原始样本；PMθ代表预测模型，θ是预测模型的参数;ε为扰动预算；α（θ）为预测得到的攻击步长。每个原始样本都会预测一个对应的攻击步长，并且随着预测模型的训练，攻击步长会得到进一步的学习。

2.2 对抗样本生成

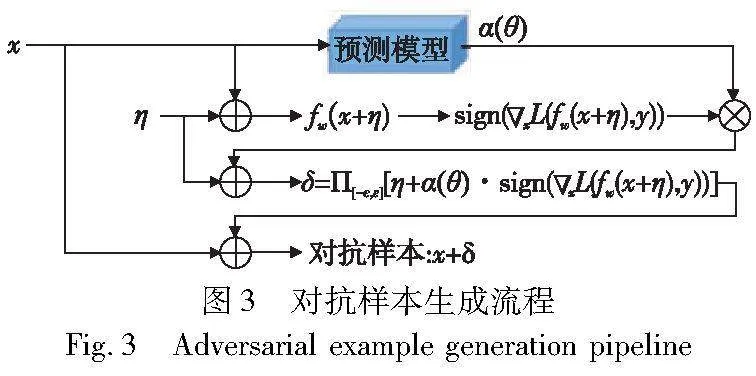
图3展示了本文方法中对抗样本的完整生成流程，主要包括以下三个步骤：

a）将原始样本x输入预测模型得到攻击步长α（θ），计算公式如式（4）所示。这个步骤的主要目的是在当前训练阶段确定对原始样本所需的扰动程度。

b）对原始样本x添加随机初始化扰动η，并将该扰动后的样本输入到目标模型中进行前向传播计算。接着，将计算出的结果与真实类别标签y进行交叉熵损失计算。然后，以损失为因变量，原始样本为自变量，进行反向传播以计算原始样本的梯度。最后，通过sign函数提取梯度的符号（1或-1），该符号指示了在扰动下原始样本的变化方向。

c）将步骤a）中计算得到的攻击步长α（θ）与步骤b）中得到的梯度符号相乘，然后将乘积与随机初始化扰动η相加。接着，对得到的结果进行投影裁剪操作（Π［-ε，ε］［·］），将其限制在-ε～ε。这样就得到了对抗扰动δ。最后，将原始样本x加上对抗扰动δ，即得到所需的对抗样本x+δ。

2.3 联合对抗训练

为了保证本文方法在训练过程中的高效性，选用FGSM算法来生成对抗样本，因为FGSM被公认为是速度最快的对抗攻击算法。然而，为了提高对抗鲁棒性，本文并未采用原生的FGSM算法。相反，本文将FGSM算法所需的攻击步长参数替换为预测模型（针对每个样本）预测出来的攻击步长。为了在训练过程中使攻击步长得到学习，本文将预测模型与目标模型进行联合对抗训练，从而使预测模型的参数得到学习。因此，通过这种方式，攻击步长的学习能力得到了提高，它可以为目标模型持续提供有效的攻击，从而防止目标模型对对抗样本产生适应性而发生过拟合。让攻击步长在训练过程中持续学习是非常重要的。

为了实现联合对抗训练，本文引入了一个超参数k。当目标模型的训练次数达到k的整数倍时，预测模型将进行一次训练。通过这种训练方式，预测模型和目标模型形成了一种相互影响的关系。预测模型的训练是为了提高目标模型的损失，以便在之后的训练中使预测模型预测的攻击步长对目标模型产生更强的攻击效果。而目标模型的训练是为了减少自身的损失，以提高自身的预测能力。在这种训练机制下，随着预测模型的不断训练，每个样本都会生成更强的对抗样本，这些对抗样本将在之后的目标模型训练中发挥作用，使目标模型的对抗鲁棒性得到显著提高。结合本文方法，对抗训练的目标可以总结为

其中：x表示数据集D中的原始干净样本；y为x的类别标签；η为随机初始化扰动；fw表示目标模型，w是模型参数；L为损失函数;x表示求x的梯度;sign为取符号函数;ε为扰动预算;δ为对抗扰动;Π［-ε， ε］表示将δ限制在-ε～ε;θ为预测模型的参数；α（θ）表示通过预测模型所预测出的攻击步长。

2.4 算法描述

本节详细介绍了本文方法的算法流程。该算法主要包含两个关键步骤：

a）对抗样本的生成。生成对抗样本需要同时使用预测模型和目标模型。首先，将原始样本输入预测模型以预测攻击步长。然后，将该攻击步长、目标模型的参数以及随机初始化后的原始样本输入 FGSM 算法，以生成对抗样本。该步骤在算法1伪代码中的第3、4、6～8行以及第3、4、11～13行中体现，对应图1中的实线部分。

b）联合对抗训练。在算法1的伪代码中，第5行如果条件成立，那么将进行一次预测模型的训练，具体如第9行代码所示。而第14行则是使用对抗样本对目标模型进行的一次训练。该步骤对应图1中的虚线部分。

算法1 基于可学习攻击步长的联合对抗训练方法

3 实验与分析

本文所有实验均在Linux平台下完成，硬件配置为AMD 5800X CPU和RTX 2080Ti GUP。

3.1 数据集介绍

在文献［12］中，FGSM-CKPT方法在CIFAR-10和Tiny ImageNet数据集［19］上进行了对比实验；文献［13］中 FGSM-GA方法则选择了CIFAR-10和SVHN数据集进行了对比实验；文献［14］中的ATAS方法则分别在CIFAR-10、CIFAR-100和 Image-Net数据集上进行了对比实验；文献［10］中的LAS-AT方法则在CIFAR-10、CIFAR-100和Tiny ImageNet数据集上进行了对比实验。为了保证与这四种方法对比的公正性，本文选择CIFAR-10、CIFAR-100和Tiny ImageNet数据集进行评估和对比实验。

CIFAR-10数据集包含60 000个样本，分为10个类别，每个类别有6 000个样本。这些样本是32×32像素的RGB图像，具有3个通道（红色、绿色、蓝色）。在CIFAR-10中，每个样本都对应一个真实的类别标签，其中50 000个样本作为训练集，10 000个样本作为验证集。

CIFAR-100数据集则有100个类别标签，每个标签包含600个样本，其中500个用于训练，100个用于验证。样本的大小和通道数与CIFAR-10相同。

Tiny ImageNet数据集有200个类别标签，每个标签有500个训练样本和50个验证样本。样本是64×64像素的RGB图像。

3.2 模型超参数设置

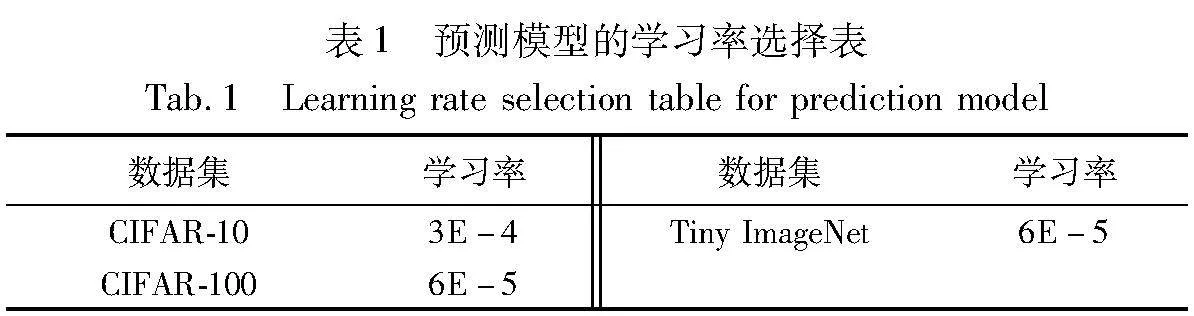
本文使用到的两个目标模型（ResNet18［20］、Preact-ResNet18［21］）和一个预测模型都将批次大小设为128，使用交叉熵损失作为损失函数，优化器使用SGD，权重衰减系数设为5E-4，动量设为0.9，训练周期数设定为110。学习率有所不同，ResNet18和PreactResNet18的初始学习率分别设为0.1和0.01，且在第100和第105次训练周期时将学习率除以10。预测模型的学习率在不同的数据集上采用不同的学习率（表1），且训练过程中不对学习率进行调整。预测模型中的扰动预算设为8/255。

3.3 超参数k的选择实验

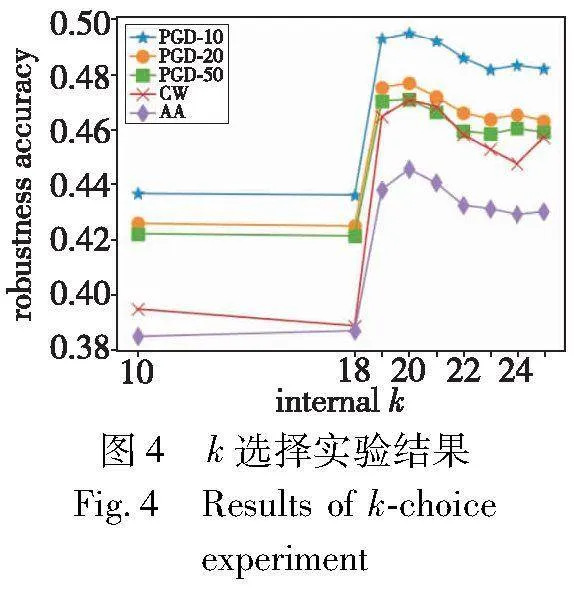
在CIFAR-10数据集上，采用FGSM-LASS对ResNet18目标模型进行对抗训练。ResNet18模型的相关超参数设置在3.2节中已详细阐述。在训练过程中，对k值进行不同的选择，以便找到最适合的超参数配置，从而获得更好的模型性能。

如图4所示的实验结果中，横坐标表示超参数k的不同取值，而纵坐标则对应了在使用FGSM-LASS训练的目标模型下，对于不同对抗攻击的鲁棒性。当k＜19时，预测模型训练过于频繁，使得其预测的攻击步长迅速饱和。在饱和后的训练过程中，生成的对抗样本难以为目标模型提供强大的攻击能力，从而导致最终的对抗鲁棒性较低。当k＞20，预测模型的训练将不够充分，这也会使得训练得到的目标模型在抵抗各种对抗攻击的能力上有所减弱。当k取值为19或20时，虽然PGD系列攻击下，实验观测到的对抗鲁棒性非常相近，但在C&W和AA攻击下，k=20时的鲁棒精度提高了近1%。因此，选择20作为超参数k的取值。

3.4 可学习攻击步长的有效性实验

FGSM-RS通过添加随机初始化来增强生成对抗样本的攻击强度。然而，该方法仍然使用了较大的攻击步长（10/255），这会导致在应用投影裁剪操作后，扰动主要集中在［-ε，ε］的边界附近。这种情况下，模型的决策边界可能会发生扭曲，使得模型容易受到较小对抗扰动的影响，从而容易被欺骗。FGSM-CKPT通过有规律地调整攻击步长，使得模型的损失增大，进而增强对抗样本的攻击强度。ATAS通过累加样本梯度范数来确定攻击步长，进而增强对抗样本的攻击效果。然而，这两种调整攻击步长的方法在提升对抗鲁棒性方面的表现并不理想。FGSM-GA通过基于梯度对齐算法来解决大攻击步长导致的决策边界扭曲问题，尽管它提高了对抗鲁棒性，但梯度对齐算法的时间成本却远高于FGSM-CKPT和ATAS。在对上述方法进行深入分析的基础上，本文提出了一种基于可学习攻击步长的联合对抗训练方法。该方法采用预测模型来预测攻击步长，并且攻击步长会随着预测模型的不断训练而得到学习。

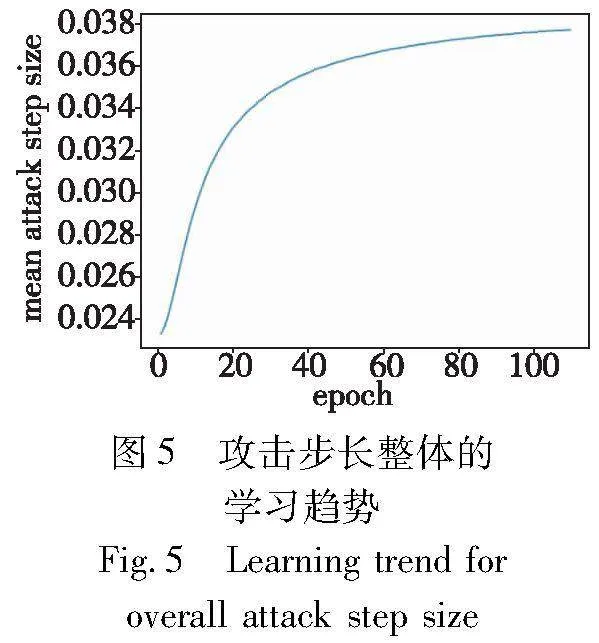
为了证明学习得到的攻击步长的有效性，在CIFAR-10数据集上训练ResNet18目标模型，并记录攻击步长均值的学习轨迹。超参数的设置已在3.2节中详细阐述，此外，k取值20。攻击步长均值的学习轨迹如图5所示。在整个训练过程中，攻击步长均值的学习趋势是逐渐增加的，这意味着在训练过程中，可学习的攻击步长能够持续为目标模型提供强有力的攻击。

为了深入验证本文所提可学习攻击步长的有效性，进行了一系列的对比实验。实验结果如图6所示，其中本文方法的实验结果如图6（e）所示，训练得到的目标模型在对抗扰动方向上的损失最高约为0.7。相比而言，FGSM-RS的实验结果如图6（a）所示，其在对抗扰动方向上的损失最高达到了2.5；FGSM-CKPT的实验结果如图6（b）所示，其在对抗扰动方向上的损失最高达到了1.95；ATAS的实验结果如图6（c）所示，其在对抗扰动方向上的损失最高达到了1.3；FGSM-GA的实验结果如图6（d）所示，其在对抗扰动方向上的损失最高约为0.98。综合以上分析，通过损失指标的对比，本文方法表现出了最优的性能。此外，在3.5节中，将通过对比分析对抗鲁棒性、训练时间等关键指标，进一步验证本文方法在性能方面相较于其他方法的优越性。

在CIFAR-10数据集上，本文采用了ResNet18作为目标模型，并使用了FGSM-RS、FGSM-CKPT、ATAS、FGSM-GA和本文方法FGSM-LASS五种对抗训练方法进行训练。为了保证比较的公平性，所有训练的常规设置都遵循了3.2节中详细阐述的超参数设置。另外，对于FGSM-RS和FGSM-GA，设定攻击步长为10/255；FGSM-CKPT和ATAS则分别使用它们自身调整的攻击步长；而FGSM-LASS则采用学习得到的攻击步长。对于未提及的其他超参数设置，本文都遵循了各自文献中的最优设置。利用各自训练好的模型，计算原始干净样本在随机扰动方向和对抗扰动方向上的损失曲面图，如图6所示。其中，x轴表示对抗扰动大小，y轴表示随机初始化扰动大小，z轴表示目标模型的损失。点（0，0）对应的损失表示使用原始样本计算得到的损失，点（1，1）对应的损失表示使用完整的对抗样本计算得到的损失。

图6（a）展示了经过FGSM-RS训练得到模型的损失曲面图。在x轴上，当对抗扰动降低到原始范围的0.3～0.7时，模型的损失显著增加，且预测结果出现偏差。然而，当大于0.7时，模型的损失较小，且预测结果正确。这正是决策边界扭曲的现象。

图6（b）展示了经过FGSM-CKPT训练得到的模型损失曲面图。该曲面在x轴上以0.7为分界点，呈现出两块不同的区域。在0.7以下，损失较小且预测精确；然而，当超过0.7时，损失增大且预测出现偏差。这一现象说明，尽管FGSM-CKPT通过有规律地调整攻击步长，成功解决了决策边界扭曲的问题，但它同时也降低了模型对较大扰动的防御能力。这也暗示，有规律地调整攻击步长并不能使模型充分学习到较大扰动的特性，从而无法产生有效的防御效果。

图6（c）展示了经过ATAS训练得到模型的损失曲面图。该方法的损失曲面图整体较为平缓，直至接近完整的对抗扰动（大于0.9）时，预测失误的风险才逐渐增大。这表明，通过使用梯度范数对攻击步长进行自适应调整，ATAS成功地解决了决策边界扭曲的问题，并使模型能够学习到较大扰动的一些特性，从而在一定程度上具备了防御较大扰动的能力。

图6（d）（e）分别展示了经过FGSM-GA和FGSM-LASS训练得到模型的损失曲面图。可以看出，这两种方法都成功地解决了决策边界扭曲的问题，并且在应对较大对抗扰动方面的防御能力都超过了ATAS。因此，可学习的攻击步长策略与梯度对齐算法的效果相当，但前者的时间成本远低于后者。

3.5 抵御对抗攻击的实验

为了验证FGSM-LASS在防御对抗攻击上的有效性，将其与FGSM-RS、FGSM-CKPT、FGSM-GA和LAS-AT进行了对比实验。为了评估这些对抗训练方法所训练的目标模型的对抗鲁棒性，本文使用了PGD-10、PGD-50、C&W和AA这四种对抗攻击方法对目标模型进行攻击，并把不同攻击下的鲁棒精度（对抗鲁棒性）作为主要的评估指标，将原始样本的分类精度以及模型训练的时间成本作为次要评估指标。

为了保证比较的公正性，所有训练都遵循了3.2节中详细阐述的超参数设置。另外，对于FGSM-RS和FGSM-GA，设定的攻击步长为10/255；FGSM-CKPT和ATAS分别采用它们各自算法调整的攻击步长；LAS-AT的攻击策略（如攻击步长、迭代次数和扰动预算）使用LAS-AT中的策略模型预测；而FGSM-LASS则使用学习得到的攻击步长。对于未在上述内容中提及的其他超参数设置，都遵循各自文献中的最佳设置。

3.5.1 CIFAR-10 & CIFAR-100

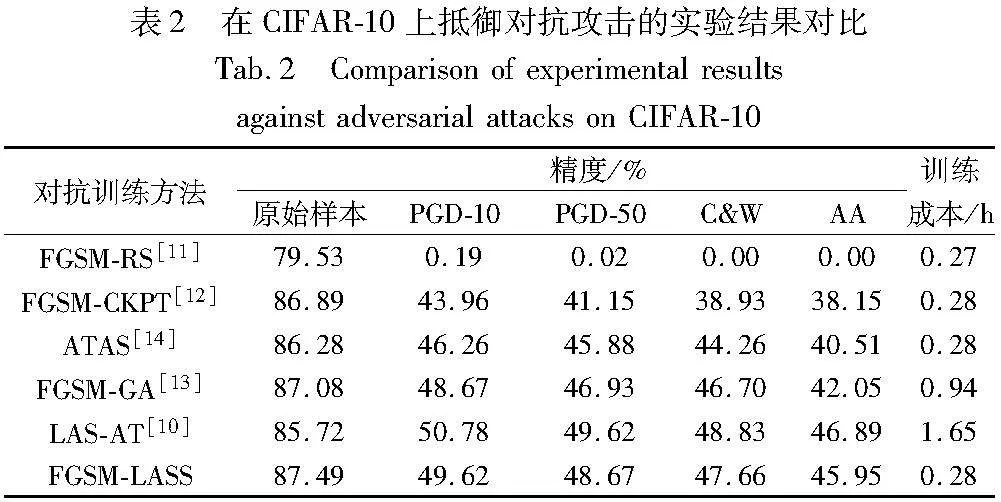
在CIFAR-10和CIFAR-100数据集上，首先使用这些对抗训练方法训练ResNet18目标模型，然后将这些训练好的模型进行对抗攻击。实验结果如表2和3所示。观察实验结果发现，经过FGSM-RS训练的模型在PGD-10、PGD-50、C&W和AA攻击下，鲁棒精度几乎降为零，这与3.4节开头部分分析的问题相符。FGSM-CKPT和ATAS通过调整攻击步长成功解决了FGSM-RS中的问题。然而，FGSM-LASS 方法在相同的训练成本下，显著提高了模型的鲁棒精度。FGSM-GA通过引入梯度对齐算法来提高模型的鲁棒精度，然而与FGSM-LASS相比，其时间成本增加了3倍多，而鲁棒精度却低了近1%。因此，在训练速度和抗干扰能力方面，FGSM-LASS都超过了FGSM-GA。相较于LAS-AT，FGSM-LASS的鲁棒精度略低约1%，但基于PGD的LAS-AT对抗训练方法需要多次迭代来计算训练所需的对抗样本，同时还需借助强化学习来训练策略模型，其训练时间成本是FGSM-LASS的近6倍。这在实际应用中是难以承受的。因此，FGSM-LASS在训练速度与对抗鲁棒性之间的平衡表现最为出色。

3.5.2 Tiny ImageNet

在Tiny ImageNet数据集上，首先使用这些对抗训练方法训练PreactResNet18模型，然后将这些训练好的模型进行对抗攻击。观察实验结果发现，在Tiny ImageNet上的实验结果与在CIFAR-10和CIFAR-100基本保持一致。实验结果如表4所示。

4 结束语

本文提出了一种预测模型用于预测攻击步长，以便在训练阶段为每个原始干净样本生成攻击强度更强的对抗样本。这些对抗样本用于预测模型和目标模型的联合对抗训练，使得预测模型预测得到的攻击步长具有学习能力，从而在保证训练速度快的同时，进一步提高目标模型的对抗鲁棒性。通过大量实验证明，该方法不仅时间成本低，而且训练出来的目标模型对抗各种攻击的能力也非常强。

当然，本文方法并非完美，其获得的对抗鲁棒性仍无法完全超越基于PGD的对抗训练。在后续的研究中，可以尝试引入一些数据增强技术以提高模型的泛化能力，从而进一步提升模型的对抗鲁棒性，有潜力超过基于PGD的对抗训练。

参考文献：

［1］Dosovitskiy A， Beyer L， Kolesnikov A， et al. An image is worth 16×16 words： Transformers for image recognition at scale［EB/OL］.（2021-06-03）. https：//arxiv.org/abs/2010.11929.

［2］Chen Xiangning， Liang Chen， Huang Da， et al. Symbolic discovery of optimization algorithms［EB/OL］. （2023-02-13）［2023-05-08］. https：//arxiv.org/abs/2302.06675.

［3］Li Chuyi， Li Lulu， Geng Yifei， et al. YOLOv6 v3.0： a full-scale Reloading［EB/OL］. （2023-01-13）. https：//doi.org/10.48550/arXiv.2301.05586

［4］Jain J， Li Jiachen， Chui M T， et al. OneFormer： one transformer to rule universal image segmentation［EB/OL］. （2022-11-10）［2022-12-27］. https：//arxiv.org/abs/2211.06220.

［5］Szegedy C， Zaremba W， Sutskever I， et al. Intriguing properties of neural networks［EB/OL］.（2014-02-19）. https：//arxiv.org/abs/1313.6199.

［6］Goodfellow I J， Shlens J， Szegedy C. Explaining and harnessing adversarial examples［C］//Proc of the 3rd International Conference on Learning Representations. 2014.

［7］Madry A， Makelov A， Schmidt L， et al. Towards deep learning mo-dels resistant to adversarial attacks［EB/OL］.（2019-09-04）. https：//arxiv.org/abs/1706.06083.

［8］Cai Qizhi， Du Min， Liu Chang， et al. Curriculum adversarial training［C］//Proc of the 27th International Joint Conference on Artificial Intelligence. San Francisco： Margan Kaufmann， 2018： 3740-3747.

［9］Ye Nanyang， Li Qianxiao， Zhou Xiaoyun， et al. Amata： an annealing mechanism for adversarial training acceleration［C］//Proc of the 35th AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2021： 10691-10699.

［10］Jia Xiaojun， Zhang Yong， Wu Baoyuan， et al. LAS-AT： adversarial training with learnable attack strategy［C］//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2022： 13388-13398.

［11］Wong E， Rice L， Koler J Z. Fast is better than free： revisiting adversarial training［EB/OL］.（2020-01-12）. https：//arxiv.org/abs/2001.03994.

［12］Kim H， Lee W， Lee J. Understanding catastrophic overfitting in single-step adversarial training［C］//Proc of the 35th AAAI Confe-rence on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2021： 8119-8127.

［13］Andriushchenko M， Flammarion N. Understanding and Improving Fast Adversarial Training［C］//Proc of the 34th Annual Conference on Neural Information Processing Systems. New York： Curran Associates， 2020： 16048-16059.

［14］Huang Zhichao， Fan Yanbo， Liu Chen， et al. Fast adversarial trai-ning with adaptive step size［EB/OL］. （2022-06-06）. https：//arxiv.org/abs/2206.02417.

［15］Wang Xiaosen， He Kun. Enhancing the transferability of adversarial attacks through variance tuning［C］//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2021： 1924-1933.

［16］Carlini N， Wagner D A. Towards evaluating the robustness of neural networks［C］//Proc of IEEE Symposium on Security and Privacy. Piscataway， NJ： IEEE Computer Society， 2017： 39-57.

［17］Croce F， Hein M. Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks［C］//Proc of the 37th International Conference on Machine Learning. New York： PMLR， 2020： 2206-2216.

［18］Glorot X， Bordes A， Bengio Y. Deep sparse rectifier neural networks［J］. Journal of Machine Learning Research， 2011，15： 315-323.

［19］Deng Jia， Dong Wei， Socher R， et al. ImageNet： a large-scale hie-rarchical image database［C］//Proc of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. PiscgIs38cxtEdZeFeDZYzTEBU5otf6yvG62bylzgd0hsMo=ataway， NJ： IEEE Computer Society， 2009： 248-255.

［20］He Kaiming， Zhang Xiangyu， Ren Shaoqing， et al. Deep residual learning for image recognition［C］//Proc of IEEE Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Computer Society， 2016： 770-778.

［21］He Kaiming， Zhang Xiangyu， Ren Shaoqing， et al. Identity mappings in deep residual networks［EB/OL］. （2016-07-25）. https：//arxiv.org/abs/1603.05027.