非正交多址系统中基于公平性改善的双层挤压迭代功率分配方法

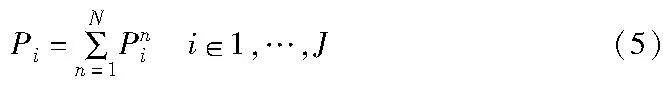
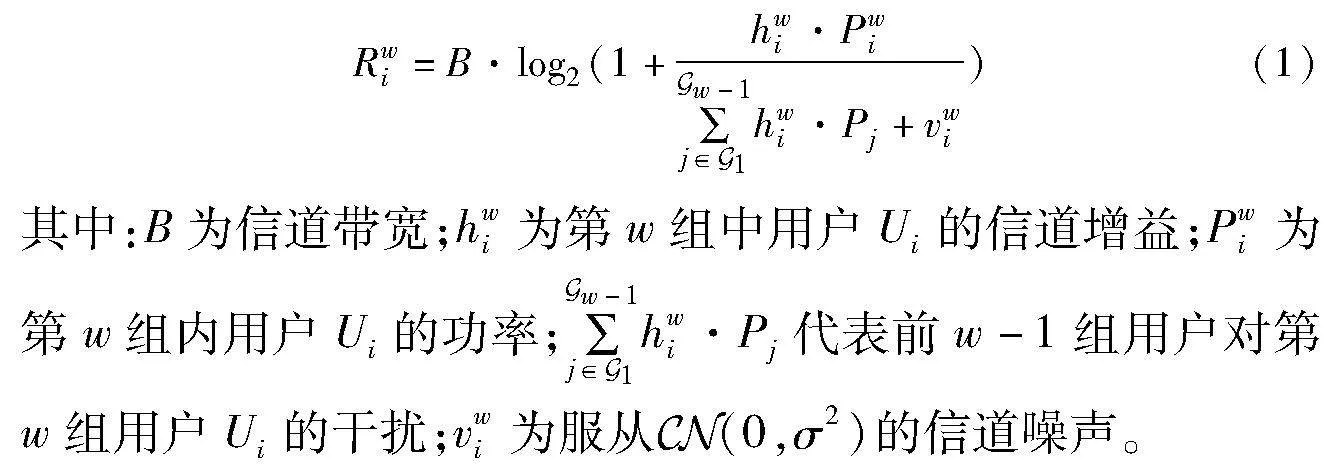
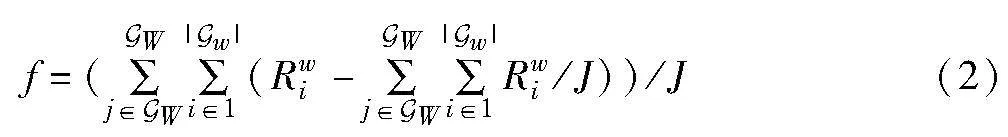
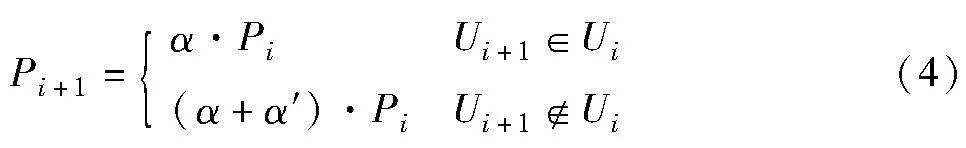
摘 要：为了解决下行非正交多址系统中多用户通信的公平性问题，提出了基于公平性改善的双层挤压迭代功率分配方法。研究内容包括：首先，设计基于用户信道增益差的用户信道分裂过程，方便动态调整功率挤压时的挤压程度；其次，从强用户到弱用户进行内层功率挤压迭代，根据信道分裂情况设置挤压因子与附加挤压因子，使信道分裂处的弱用户对强用户挤压程度更强；第三，对内层挤压功率进行外层迭代的再分配与再挤压，可保持总功率不变的情况下，进一步提升功率分配的公平性。仿真结果表明：对比信道分裂下与信道未分裂下的公平性指数，其性能提升了25%；对比仅进行挤压因子与附加挤压因子调整，而未进行内外层迭代次数调整的情况，公平性指数性能提升了53.71%，同时，所提算法比注水算法达到的公平性指数明显改善，在公平性提升方面达到了较好的效果。

关键词：非正交多址； 公平性； 功率挤压； 双层迭代

中图分类号：TN929.5 文献标志码：A

文章编号：1001-3695（2024）06-031-1815-05

doi：10.19734/j.issn.1001-3695.2023.10.0503

Double layer squeeze iterative power allocation method based on fairness

improvement in non-orthogonal multiple access systems

Abstract：In order to improve the fairness of downlink non-orthogonal multiple access systems， this paper proposed a dual layer squeezing iterative power allocation method based on fairness improvement . Firstly， it designed a user channel splitting process based on user channel gain difference to facilitate dynamic adjustment of the degree of power squeezing. Secondly， it carried out the inner power squeezing iteration from strong users to weak users， and set the squeezing factor and additional squeezing factor according to the channel splitting situation， so that the weak users at the channel splitting point had a stronger squeezing degree towards the strong users. Thirdly， the reallocation and resqueeze of the inner power through outer iteration could further improve the fairness of power distribution， while maintaining the total power unchanged. The simulation results show that compared with the fairness index without channel splitting， it can improve the fairness with channel splitting by 25%; Compared to the situation that the squeezing factor and additional squeezing factor are only adjusted without the number of inner and outer iterations adjustment， it improves the fairness index performance by 53.71%. Meanwhile， the fairness of proposed algorithm is better than the waterfilling algorithm and gained a good fairness effect.

Key words：NOMA; fairness; power squeeze; double iteration

0 引言

当前移动通信面临用户数量急剧增长的趋势，需要新型多址技术来应对挑战［1，2］，非正交多址（non-orthogonal multiple access，NOMA）技术在相同时频资源下能够接入更多用户，可有效提升用户接入数量，改善频谱效率［3，4］。

当前已提出多种NOMA技术，例如功率域多址、稀疏码多址、图样分割多址、多用户共享多址等［5～7］。功率域非正交多址在学术界研究较多，对于下行功率域非正交多址，在发射端，基站根据用户信道状态信息进行用户功率分配，传输多用户的叠加信号；在接收端，用户采用串行干扰消除技术消除其他用户干扰来解码自身用户信息。在功率域非正交多址中，功率分配对用户通信性能起到关键作用，近用户由于位置优势，信道状态条件好，通信效果好；而远用户则反之。如果不考虑这些情况，而是将基站功率平均分配给用户，会使用户间失去公平性，尤其会对弱用户造成较大的影响［8］。

文献［8］针对上行功率域非正交多址提出了一个新的公平性定义方法，该方法基于信息理论，在接收总功率与用户分布确定的情况下研究用户的公平性，仿真计算只应用于2用户非正交多址系统中。文献［9］比较了非正交多址NOMA方案和正交多接入OMA（orthogonal multiple access）方案之间上行链路通信的资源分配公平性，提供了在NOMA和OMA之间进行选择的标准，以实现公平的资源分配，主要适用于增强混合NOMA-OMA方案的公平性。文献［10］提出了一种低复杂度基于注水的功率分配PA（power allocation）技术，该技术联合子带调度保证资源分配的高水平公平性，主要适用于多子带的通信系统中。文献［11］提出了一种基于功率最小化的IRS（intelligent reflecting surface）辅助上行NOMA系统资源分配方法，该方法主要解决在智能反射面辅助场景中功耗如何优化的问题。文献［12］研究调整多小区基站的发射功率实现多小区蜂窝网络的和速率最大化，提出的DDPG（deep deterministic policy gradient）算法相较于传统算法和速率提升了34.2%。文献［13］通过联合设计RIS相移矩阵、基站端波束赋形以及NOMA系统串行干扰消除顺序来最小化系统的总发射功率，以减轻通信系统中基站的能耗负担。文献［14］针对蜂窝网络非正交多址接入系统，为了提高系统的能量效率减少功率消耗，提出了一种基于系统能量效率最大化的非正交多址接入系统功率分配算法。文献［15］提出了上行NOMA系统中低复杂度的最大化系统能量效率的功率分配方案，结果表明随着信噪比的变化，该方案的系统能量效率高于或等于相同场景中的已有方案。上述方案大多聚焦于改善系统的能量效率，对给定功率下的非正交多址系统中多用户的通信公平性改善未见研究。

本文针对功率域非正交多址下行通信公平性改善的问题，提出一种非正交多址系统中基于公平性改善的双层挤压迭代功率分配方法，具体内容如下：a）设计了功率域用户信道分裂过程，将用户按照信道增益信息大小降序排列，计算相邻用户间的信道增益差，并与阈值进行对比，形成多个用户组，组内用户信道增益差小，组间用户信道增益差大；b）根据信道分裂情况，设计内外层迭代挤压的功率分配方法，该方法利用弱用户挤压强用户功率的思想，设计功率挤压因子，并在信道分裂处挤压程度更强。同时，算法通过联合调整挤压因子、附加挤压因子、内层迭代次数与外层迭代次数四个参数进行功率分配优化，以实现用户间较高的公平性。

1 系统模型

假设无线通信系统中有1个基站，J个用户，基站与用户间进行下行通信。将J个用户信道状态信息进行降序排列，设为用户间信道增益差阈值，当相邻用户间信道增益差大于时，信道分裂，如图1所示。用户按照信道分裂情况进行分组，在信道分裂处开启新的用户小组，组间用户信道增益差大，组内用户信道增益差小。

假设所有用户分成了W个用户组，可表示为Euclid Math OneGAp=［Euclid Math OneGAp1，…，Euclid Math OneGApw，…，Euclid Math OneGApW］，w∈［1，2，…，W］，每组用户集合表示为Euclid Math OneGApw=［Jwi］［Jw1，…，Jwi，…，Jw|Euclid Math OneGApw|］，w∈［1，2，…，W］，i∈［1，2，…，|Euclid Math OneGApw|］。其中，|Euclid Math OneGApw|≥1为第w组内的总用户数。对任一用户i∈Gw来说，用户速率Rwi可表示为

由于用户距离基站的远近不同，在下行通信中对远用户造成不公平，需要对基站的发射功率进行合理分配，以改善用户的公平性。定义公平性指数f为

公平性指数f描述了系统中所有用户的传输速率与系统平均速率的偏离程度，公平性指数越小越好。影响公平性指数的关键是基站的功率分配，形成的优化问题P1可表示为

其中，优化的目标是使公平性指数最小。限制条件C1表示每个用户的功率不能为负；限制条件C2表示，针对组间用户，排序索引值较小的用户组的功率分配应当不大于排序索引值较大的用户组的功率分配；限制条件C3表示，针对组内用户，排序索引值较小的用户的功率分配应当不大于排序索引值较大的用户的功率分配；限制条件C4表示所有用户的分配功率之和不超过基站总功率。由于P1是非凸的NP-hard问题，本文提出了一个基于公平性改善的双层挤压迭代功率分配方法（double layer squeeze iterative power allocation method based on fairness improvement，DLSI）。

2 基于公平性改善的双层挤压迭代功率分配方法DLSI

DLSI按照一定比例逐个挤压较强用户的功率，将挤压功率传递给较弱用户，保证弱用户传输速率得到改善，以提升系统整体公平性。在挤压功率的过程中设计了挤压因子、附加挤压因子、内外层挤压迭代次数四个重要参数，通过对参数不断调整，实现公平性指数的提升。

2.1 信道分裂

2.2 内层功率挤压迭代

a）设置内层功率挤压迭代次数为q。

b）功率初始化。设基站的发射总功率为Ptot，先将发射功率平均分给每个用户，各用户初始功率为Ptot/J。

c）内层功率挤压。考虑公平性，系统应总是照顾更弱的用户，弱用户应比强用户得到更多功率，以抵抗强用户的干扰，从而提高弱用户的传输速率。基于该分配思想，设计两个参数α与α′，α称为挤压因子，α′称为附加挤压因子，且1>α>α′。具体的内层功率挤压过程如下：

（a）信道增益降序排列，相邻用户间，索引较大（较弱）的用户对索引较小（较强）的用户按一定比例挤压功率，挤压出的功率归较弱用户所有，保证较弱用户获得比较强用户更多的功率分配。挤压功率的大小可按式（4）进行计算。

其中：Pi+1与Pi分别为用户Ui+1与Ui的功率。式（4）说明，用户Ui+1与Ui属于同一组时，从用户Ui中挤压的功率大小为α·Pi，挤压比例为挤压因子α；当用户Ui+1与Ui不属于同一组时，需从用户Ui拿走更多的功率来补偿用户Ui+1，因此将挤压因子调大至α+α′，即在发生信道分裂的弱用户处需要调整挤压因子，此时挤压比例更大。按照式（4）的挤压功率方法，可以保证较弱用户比较强用户得到更大的功率分配，且在新用户组的第一个用户成员处（信道分裂），挤压程度更大。

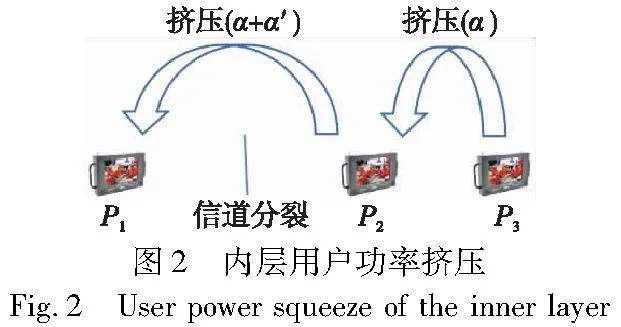
以三个用户为例进行说明，如图2所示。首先将三个用户按信道增益大小降序排列，假设初始时3个用户的分配功率相等，均为P。用户1前面没有用户，不进行挤压；用户2挤压用户1，由于用户2处发生了信道分裂，用户2为下一用户组的第一个用户，所以挤压比例为α+α′，挤压出的功率大小为（α+α′）·P，此时，用户2的功率大小为P+（α+α′）·P；用户3挤压用户2，由于用户2与3属于同一用户组，挤压出用户2的功率大小为α·（P+（α+α′）·P），挤压比例为挤压因子α，此时用户3的功率大小为P+α·（P+（α+α′）·P）。由此可以看出，用户2在挤压用户1之后，得到了比初始平均功率更大的功率；用户3在用户2增大了的功率基础上，挤压用户2的功率，虽然挤压因子为α，但是挤压的功率总量变大，则挤压出的功率变大，因此，用户3得到了比用户2更大的功率。

（b）每个用户减去被相邻弱用户挤压走的功率，保证各用户分配的功率之和与发射总功率Ptot相同。

仍以上述三个用户为例，用户1减去用户2挤压走的功率（α+α′）·P；用户2减去用户3挤压走的功率α·（P+（α+α′）·P），而用户3后面没有用户，直观的想法是用户3不再减除功率，虽然能够保证3个用户的功率之和等于Ptot，但可能会造成用户3的分配功率过大，对其他用户造成严重不公平。

该算法中提出的解决方案是仍需按照比例将最弱用户的功率进行挤压，即用户3减去功率α·（P+α·（P+（α+α′）·P）），这部分从用户3挤压出的功率实际上是从首用户至末用户挤压传递的功率累加。返回步骤c）进行迭代，直至迭代次数等于q。将q次内层功率挤压的结果求和，记为Pinner。

2.3 外层功率挤压迭代

外层功率挤压迭代是内层挤压功率的再分配与再挤压。在内层迭代结束后，各用户具有的功率大小为P1i，且P1i+1>P1i，i∈1，…，J，P1i表示用户Ui在上一轮内层功率挤压后的功率大小。将Pinner平均分给J个用户，此时每个用户的功率大小为Pinner/J，返回步骤c），对上一轮内层挤压出来的功率进行再分配再挤压。引入外层迭代次数k，当迭代次数达到k时，算法停止。

最后，各用户的功率可表示为

算法1 基于公平性改善的双层挤压迭代功率分配方法

3 仿真计算

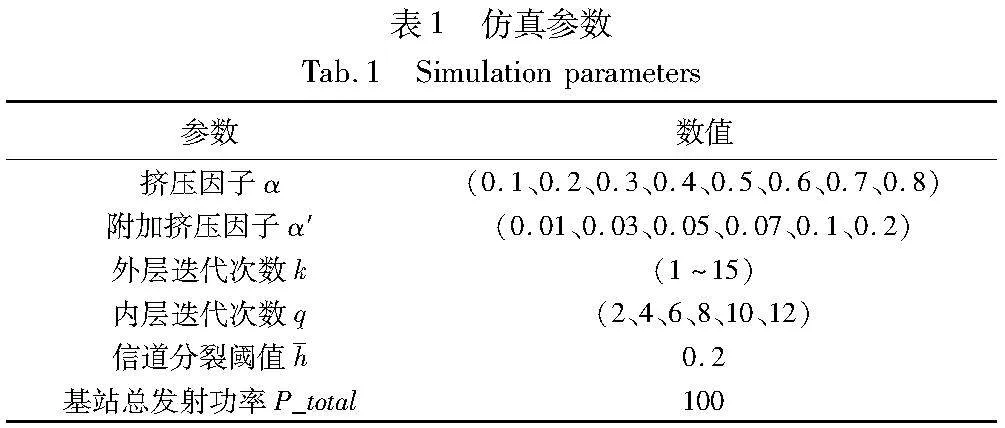
假设小区中心设置有一个基站，小区内随机分布了7个用户，假设7个用户的信道状态信息已知，将这7个用户根据信道状态信息进行降序排列，然后再根据信道分裂阈值进行信道分裂，形成多个用户组，仿真参数如表1所示。

3.1 调整挤压因子与附加挤压因子的仿真计算

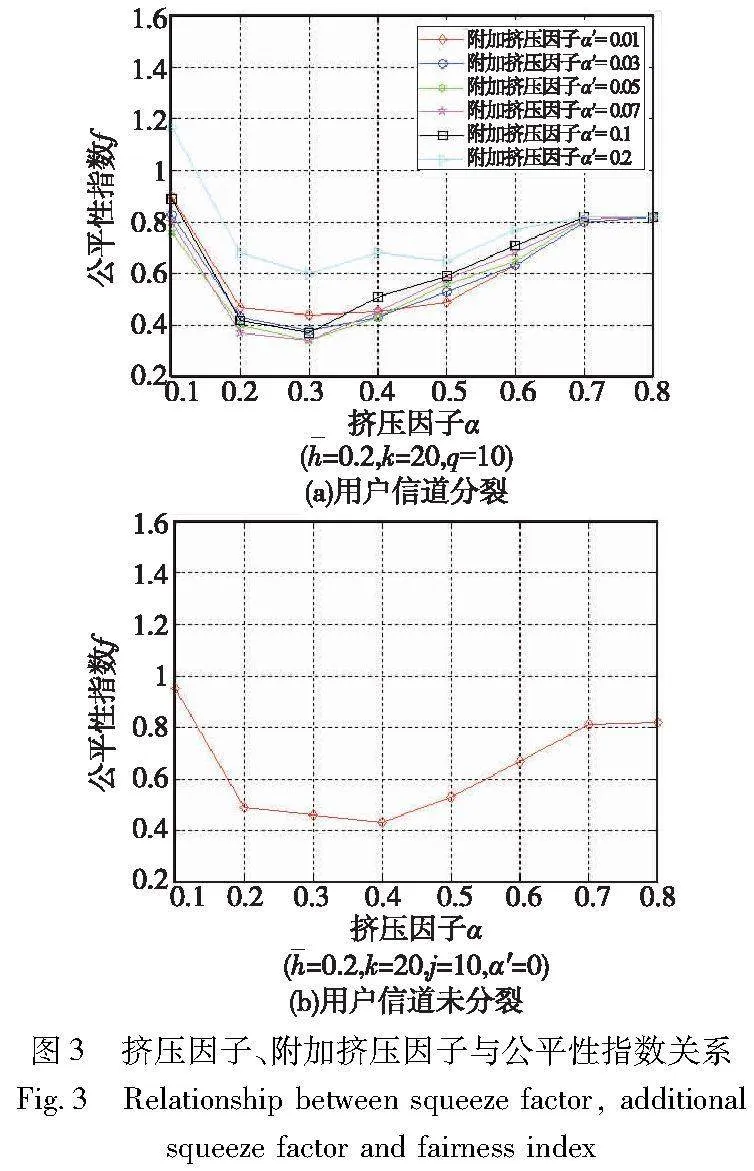
图3（a）是DLSI算法在信道分裂情况下对用户进行功率分配得到的公平性指数变化情况，图3（b）是DLSI算法在信道未分裂的情况下对用户进行功率分配得到的公平性指数变化情况（α′=0）。从图3可以看出，公平性指数的变化是先减小后增大，这是因为随着挤压因子的增大，给弱用户分配的功率逐渐增大，使得公平性指数逐渐改善。当挤压因子不断增大，公平性指数逐渐升高；当挤压因子继续增大而给弱用户分配的功率过大时，又会导致公平性指数劣化；当挤压因子大到一定程度，由于总功率有限，会使公平性趋于不变。所以，挤压因子过小过大都不行。

附加挤压因子可对信道分裂用户调整功率分配，通过对裂变用户更大比例的功率补偿来提升公平性指数。对比图3（a）中在α=0.3，α′=0.07时达到的最小公平性指数0.339 1，图3（b）在附加挤压因子α′=0的情况下达到的最小公平性指数为0.425 3，说明在相同的迭代次数下，未进行信道裂变时的功率分配使公平性下降了25%。因此挤压因子与附加挤压因子的综合调整比单一使用挤压因子调整可达到更好的公平性。

3.2 调整内、外层迭代次数的仿真计算

图4是在内层迭代次数与外层迭代次数变化时，分别针对用户信道分裂与用户信道未分裂下公平性指数的变化情况。迭代次数的调整是在挤压因子与附加挤压因子固定的情况下进行的，为α=0.3，α′=0.07，是图3（a）中使公平性指数最低时对应的参数值。在该参数下，通过调整内外层迭代次数，寻找使公平性指数更低的功率分配。图4（a）中的各条曲线总体上随着外层迭代次数k的增加而快速饱和，这是由于在挤压因子与附加挤压因子调整阶段已经锁定了公平性指数最佳时对应的参数值，所以不需要太多次的外层迭代就可以找到最佳公平性指数。

针对内层迭代次数，从图4（a）中可以看到，当q=2时，公平性指数最高，这是由于内层对功率的挤压次数少，挤压功率小，即使增大外层迭代次数进行多次功率的再分配，也不能够对弱用户进行足够的功率补偿，所以公平性低。随着内层迭代次数逐渐增大（q=4，6，8），公平性指数逐渐改善，这是由于增大的内层迭代次数会增加功率的挤压，对弱用户的功率补偿力度加大；当内层迭代次数太大（q=10，12），又会使公平性指数变差，这是因为挤压功率过大，对强用户过分挤压而对弱用户过度补偿造成的。

对比图4（a）在内层迭代次数q=6，外层迭代次数k=1时获得最佳公平性指数0.220 6，图4（b）在相同条件下所能达到的最佳公平性指数为0.277 0，性能下降25%。同时，与仅进行了挤压因子与附加挤压因子调整的图3（a）（公平性指数为0.339 1）相比，性能提升了53.71%。这说明挤压因子、附加挤压因子、内层迭代次数与外层迭代次数四个参数的联合调整，可极大改善公平性指数，同时，也可降低迭代次数，从而降低计算复杂度。

3.3 计算功率分配与用户速率的仿真计算

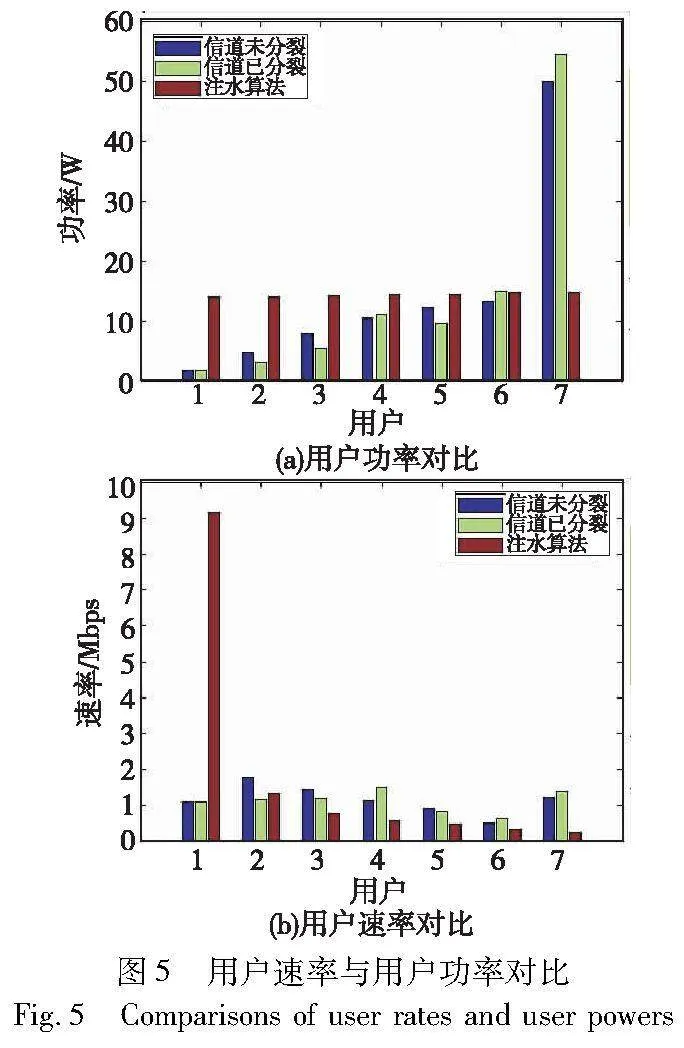
图5对比了DLSI算法与经典注水算法的功率分配。从图5（a）中可以看出，DLSI算法的功率分配结果体现了强弱用户功率分配的差异性，对弱用户进行了充分的补偿。在7个用户中，用户6为分裂用户，可以看出用户6在信道已分裂算法中相比未分裂算法下获得了更高功率，速率提升了21.41%，而注水算法在用户功率分配时的差异程度不明显。从图5（b）可以看出，DLSI算法与注水算法由于功率分配情况不同，所获得的用户间传输速率的公平性结果也不同，DLSI算法在信道分裂和信道未分裂情况下得到的各用户速率的均匀程度要明显好于注水算法。注水算法的公平性指数为2.091 8，远高于DLSI算法的公平性指数0.220 6。

4 算法性能与计算复杂度分析

4.1 算法性能分析

本文所提出的功率分配算法中有四个重要参数在算法执行中可进行调整，以获得更佳的公平指数，四个参数如表1所示。

挤压因子α的大小代表每一次内层迭代时，由强用户向弱用户挤压功率的基本比率大小。α较大，可能会挤压过强，使功率传递给弱用户的数量过大，且内外层迭代次数越多，挤压功率越大，可通过降低内外层迭代次数q、k进行调整；α较小，可能会挤压不足，使功率传递给弱用户的数量过小，可以通过增加内外层迭代次数q、k来调整。

附加挤压因子α′是对挤压因子α的补充，主要用于相邻组间用户（该用户与前面相邻用户信道增益差满足阈值条件）进行功率挤压时的附加比率，使信道分裂处的弱用户对强用户的挤压程度更强，满足更弱用户获得更多功率的基本思想。

内层功率迭代次数q代表了从强用户到弱用户的功率挤压次数，可对挤压功率大小起到调节作用，迭代次数越大，相同条件下挤压功率越大，反之则越小。内层功率挤压的意义在于从强用户到弱用户按比例逐次进行功率挤压，仍可通过调整内层迭代次数来控制各用户的功率分配，达到更好的公平性。

外层功率迭代次数k是指在每q次内层迭代挤压（即一轮内层挤压）之后，对从末用户挤压出的总功率在各用户处进行再分配与再挤压的次数。在每次进行外层迭代时，都会再经历一轮内层挤压，外层功率迭代的意义是保持总功率不变的情况下，进一步提升功率分配的公平性。

四个参数的综合调整保证了功率分配过程中，挤压程度不会一次性过大或过小而使用户间发生较强的不公平，同时也能将挤压出的功率通过多次再分配再挤压过程而进一步提升公平性。

4.2 计算复杂度分析

本文算法中包括加法和乘法运算，在每一轮内层功率挤压过程中，乘法的运算次数为q·J2/2，加法的运算次数为q·J2/2。外层功率再分配的迭代次数为k，每次迭代中乘法和加法的运算次数均为k·J2/2，因此，算法总的加法运算和乘法运算次数均为k·q·J2/2，计算复杂度随着用户数量与内外层迭代次数的增加而增加。由于参数的联合调整可使内外层迭代次数较小，所以DLSI算法的复杂度主要与J2成正比。

5 结束语

本文提出了一种下行非正交多址系统中基于公平性改善的双层挤压迭代功率分配方法，该方法根据用户信道分裂情况，对用户进行功率的内层迭代挤压与外层功率的再分配再挤压，通过对挤压因子α、附加挤压因子α′、内层迭代次数q与外层迭代次数k四个参数的综合调整，挤压程度不会一次性过大或过小，也能将挤压出的内层功率通过外层迭代的再分配再挤压进一步提升公平性。仿真结果表明，在信道分裂时获得的最佳公平性指数为0.220 6，比未进行信道分裂下的公平性指数性能提升25%。同时，与仅进行了挤压因子与附加挤压因子（公平性指数为0.339 1）而未进行内外层迭代次数调整的情况相比，公平性指数性能提升了53.71%。同时，与经典注水算法相比，本文算法的公平性指数更低。

参考文献：

［1］Saito Y， Kishiyama Y， Benjebbour A， et al. Non-orthogonal multiple access（NOMA） for cellular future radio access［C］//Proc of the 77th IEEE VTC. Piscataway，NJ：IEEE Press， 2013：1-5.

［2］Dai Linglong， Wang Bichai， Yuan Yifei， et al. Non-orthogonal multiple access for 5G： solutions， challenges， opportunities， and future research trends［J］. IEEE Communications Magazine， 2015，53（9）： 74-81.

［3］Ding Zhiguo，Liu Yuanwei，Choi J，et al. Application of non-orthogonal multiple access in LTE and 5G networks［J］. IEEE Communications Magazine， 2017，55（2）： 185-191.

［4］翟道森， 姜叶， 李欢. 基于非正交多址的空中基站MEC资源分配技术［J］. 航空科学技术， 2023，34（8）： 77-85. （Zhai Daosen， Jiang Ye， Li Huan. MEC resource allocation technology for aerial base station based on NOMA［J］. Aeronautical Science & Technology， 2023，34（8）： 77-85.）

［5］Liu Yuanwei， Qin Zhijin， Elkashlan M， et al. Nonorthogonal multiple access for 5G and beyond［J］. Proc of the IEEE， 2018，105（12）： 2347-2381.

［6］Shirvanimoghaddam M，Dohler M，Johnson S J，et al. Massive nonor-thogonal multiple access for cellular IoT： potentials and limitations［J］. IEEE Communications Magazine， 2017，55（2）： 55-61.

［7］Dai Linglong， Wang Bichai， Ding Zhiguo， et al. A survey of nonor-thogonal multiple access for 5G［J］. IEEE Communication Surveys & Tutorials， 2018，20（3）： 2294-2323.

［8］Gui Guan，Sari H，Biglieri E. A new definition of fairness for nonor-thogonal multiple access［J］. IEEE Communications Letters， 2019，23（7）： 1267-1271.

［9］Wei Zhiqiang， Guo Jiajia， Wing D K， et al. Fairness comparison of uplink NOMA and OMA［C］//Proc of the 85th IEEE VTC. Pisca-taway，NJ：IEEE Press， 2017： 1-6.

［10］Hojeij M R， Abdel N C， Farah J， et al. Waterfilling-based proportional fairness scheduler for downlink non-orthogonal multiple access［J］. IEEE Wireless Communications Letters， 2017， 6（23）： 230-233.

［11］田心记， 王坤， 李兴旺. 基于功率最小化的IRS辅助的上行NOMA系统资源分配方法［J］. 电子与信息学报， 2023， 45（6）： 1-5. （Tian Xinji， Wang kun， Li Xingwang. IRS-aided uplink NOMA systems resource allocation scheme based on power minimization［J］. Journal of Electronics & Information Technology， 2023，45（6）： 1-5.）

［12］吴建岚， 刘全金， 毕松姣，等. 多小区NOMA通信系统的强化学习功率分配算法［J］. 安庆师范大学学报：自然科学版， 2023，29（2）： 49-55. （Wu jianlan， Liu Quanjin， Bi Songjiao， et al. Reinforcement learning power allocation algorithm for multi-cell NOMA communication system［J］. Journal of Anqing Normal University：Natural Science Edition， 2023，29（2）： 49-55.）

［13］季薇， 赵亚楠， 刘子卿，等. 面向服务质量的RIS辅助的多用户NOMA服务系统功率分配方案［J］. 电子与信息学报， 2023，45（10）： 1-9. （Ji Wei， Zhao Yanan， Liu Ziqing， et al. QoS-oriented power allocation scheme for multi-user NOMA system assisted by RIS［J］. Journal of Electronics & Information Technology， 2023，45（10）： 1-9.）

［14］杨普， 曲庆悦， 申逸飞，等. 能量效率最大化的NOMA系统功率分配方法［J/OL］. 吉林大学学报：工学版.（2023-01-19）. https：//doi. org/10.13229/j.cnki.jdxbgxb20221267. （Yang Pu， Qu Qingyue， Shen Yifei， et al. NOMA power allocation scheme based on system energy efficiency maximization［J/OL］. Journal of Jilin University：Engineering and Technology Edition.（2023-01-19）. https：//doi.org/10.13229/j.cnki.jdxbgxb20221267.）

［15］田心记， 黄玉霞， 李晓静. NOMA系统中最大化能量效率的功率分配［J］. 电子科技大学学报， 2021，50（1）： 1-7. （Tian Xinji， Huang Yuxia， Li Xiaojing. Power allocation with maximizing energy efficiency for NOMA system［J］. Journal of University of Electro-nic Science and Technology of China， 2021，50（1）： 1-7.）