考虑实时订单更新的拼车调度双层规划模型

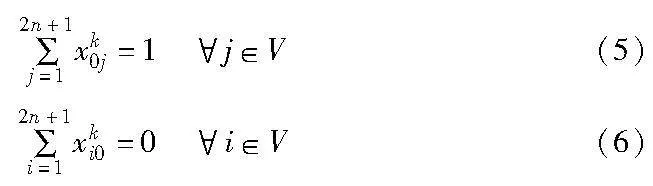
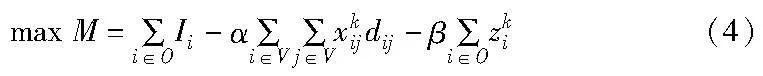
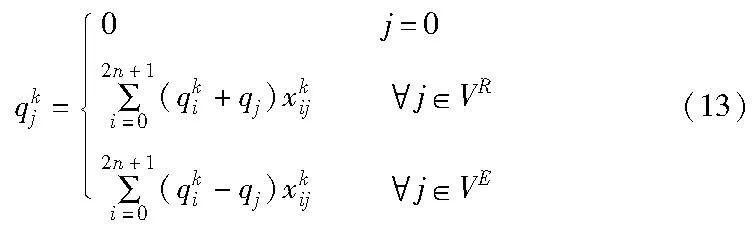
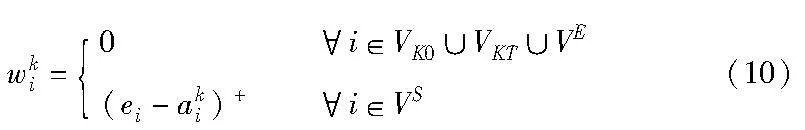
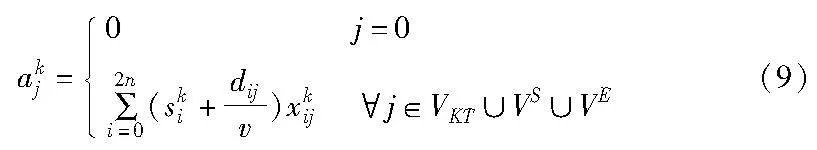
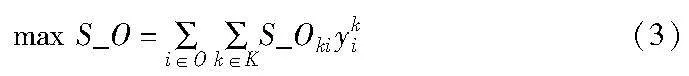
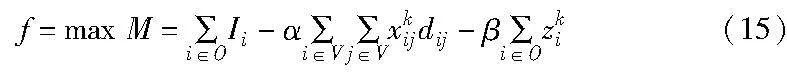
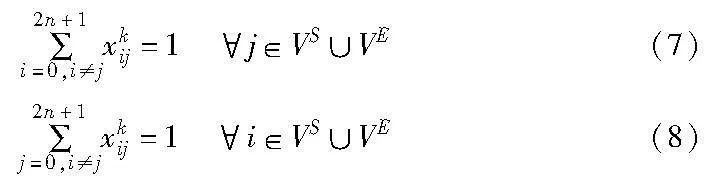
摘 要：针对订单实时更新的实际情况，为仍有待完成订单的司机持续分配任务，在保证司机收益增加的同时，提升拼车平台的派单效率。在考虑拼车系统服务质量与运行成本的基础上，基于平台角度构建了以司机总收益最大化为目标的双层规划模型，并给出求解该模型的双层算法：底层模型对拼车路径进行规划，设计改进的遗传算法求解；上层模型决定订单分配的顺序，通过贪心算法调用底层模型，比较收益变化后得到最终的调度结果。通过具体算例对模型进行验证，结果表明模型能够较快求解出订单匹配结果及行驶路线，说明了模型的可行性及算法的有效性，且计算结果能够反映实际场景。对比实验结果表明，模型在满足提升司机收益的基础上，能有效减少延误时间及降低行驶距离，对于实时订单更新场景下拼车调度问题的相关研究具有积极的参考意义。

关键词：网约拼车； 匹配策略； 路径优化； 双层算法

中图分类号：TP18; U491 文献标志码：A

文章编号：1001-3695（2024）06-016-1714-08

doi：10.19734/j.issn.1001-3695.2023.09.0438

Double-layer scheduling model for carpooling serviceconsidering dynamic order-updating

Abstract：To effectively address the real-time updates of passenger demand orders on online carpooling platforms， this paper proposed an algorithm for continuously assigning orders to drivers with unfinished orders. The proposed algorithm ensured an increase in driver earnings while enhancing the dispatch efficiency of the carpooling platform. Specifically，this paper developed a double-layer scheduling model which maximized the total driver revenue on the basis of the service quality and operational costs of the carpooling system， and proposed a double-layer algorithm for this model. The bottom layer involved the construction of a model for the carpooling routing problem， which was solved by using an improved genetic algorithm. The upper layer determined the order of task assignments， which adopted the greedy algorithm to call the model in the botton layer and compared revenue changes to obtain the final scheduling result. The model demonstrated its effectiveness and feasibility through a specific example， validating the prompt determination of order matching results and travel routes. The calculated results faithfully reflect real-world scenarios. Comparative experiments shows that the model not only achieves the goal of increasing driver earnings， but also effectively reduces delay time and travel distances. This has positive reference significance for related studies on carpooling scheduling problems in the context of real-time order updates.

Key words：ridesplitting; matching strategy; routing optimization; double-layer algorithm

0 引言

当前我国交通需求类型多样、数量日渐增多，在移动互联网技术的迅猛发展下，以网约车服务为代表的新兴出行系统取得了显著成功，成为人们日常出行的重要组成部分［1，2］。网约车平台采用多种策略，为不同类型的乘客群体提供多种服务模式，例如快车、尊享和拼车等，从而为乘客提供更精细化的服务和更好的乘坐体验［3］。

拼车模式可以在有限的车辆资源下，提供更多的出行服务，从而提高车辆的利用率［4］。拼车服务根据乘客的需求，实时动态地调整行驶路线，其收费也通常低于常规的网约车［5］。在进行订单匹配时，平台需要综合考虑乘客的出行请求和司机的状态，而司机与乘客的状态也随着调度方案的调整而不断变化。拼车调度问题受到搭乘地点、时间窗口、搭乘路线、车辆乘客容量以及行驶速度等多种变量的约束，相对比较复杂［6］。

许多学者对拼车问题进行了研究，关注于为特定状态下的司机和乘客进行匹配及调度。这种静态的订单分配要求司机完成服务后才能接受新的订单，导致司机等待接单时间较长。此外，平台在订单分配时并未考虑司机的收益变化，导致司机为更多乘客提供服务但收益不增反降。因此，针对订单实时更新的实际情况，如何为仍有待完成订单的司机持续分配任务，以减少其等待接单时间，同时确保插单后司机收益增加，成为本文研究的核心问题。

1 相关研究

拼车匹配优化主要是指将有拼车需求的乘客与运营车辆进行合理配置，从而提高拼车成功率和服务效率［7］。当前拼车优化调度主要有匹配优化、路径优化，还有匹配和路径组合优化三个方向［8］。

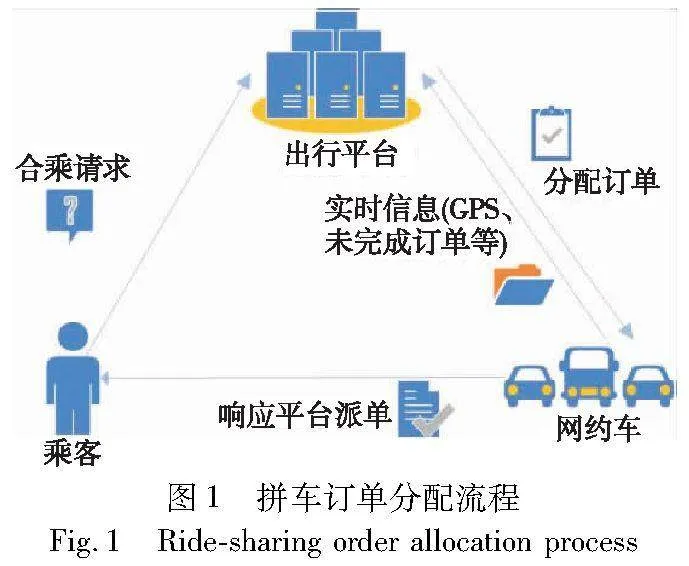
拼车服务中，乘客向平台发出合乘请求，平台整合车辆与乘客双方信息，对多车多乘客进行匹配，给出匹配方案并规划每辆车的行驶路径，图1展示了拼车订单分配的流程。近年来，订单分配问题受到了许多专家学者的广泛研究，主要涉及最小化乘客等待时间、最大化匹配率和最大化整体收益等。Qian等人［9］将出行起点和目的地相似的乘客进行分类，并优化出一个最佳的碰面点，以该碰面点作为基点与等待派单的司机进行匹配。Vazifeh等人［10］将精确的最小车队规模优化问题转换为最小路径覆盖问题，提出解决最小车队问题的最优化计算方案。滴滴出行［11］提出了一个基于深度强化学习与半马尔可夫决策过程的智能派单系统，利用深度神经网络进行价值评估。吴玥琳等人［12］针对综合客运枢纽出租车停靠点乘客滞留问题，设计两阶段算法求解合乘匹配方案及路径问题。Kucharski等人［13］提出了基于需求的合乘出行匹配算法，利用效用函数替代时间窗口，以节省费用为目标对共享网络进行优化。De Palma等人［14］模拟了动态的拼车行为，并计算每位乘客的出发时间与路线选择。

在拼车出行服务的优化中，拼车路径规划算法直接影响着司机的工作效率、乘客的出行体验以及平台的盈利情况。将司机与拼车订单匹配后，对拼车的路径进行优化，这将拼车问题转换为多个特殊的开放式的车辆路径优化问题，每个问题都只包含一辆车及多个服务节点［15］。Masoud等人［16］提出一种解决实时拼车匹配问题的优化算法，引入动态交换机制，避免“先到先服务”规则的不利影响。郭羽含等人［17］针对长期车辆合乘问题，将具有相同目的地的用户进行合乘匹配，设计了复合变邻域搜索算法。Xu等人［18］提出了一种基于马尔可夫决策过程的大规模订单分配算法，旨在整体提高司机的收入。Hou等人［19］也提出了一种拼车优化模型，先根据乘客的出行需求与车辆进行最优匹配，然后对匹配后的车辆路径进行优化。Braverman等人［20］提出一种封闭排队网络模型，通过控制网络中的车辆流动来优化整个系统，证明了优化后的网络路径分布具有稳定性。Chen等人［21］提出封闭社区内通勤者共享出行问题，考虑返程限制、会面位置以及司乘间的互相选择，提出整数线性规划模型，并给出了对应的启发式算法。

拼车调度问题类似于接乘问题PDP（pickup and delivery problem），属于NP问题（non-deterministic polynomial）的范畴。拼车调度研究领域，国内外许多学者致力于改进创新匹配和路径规划模型及求解算法。Simonetto等人［22］提出两种拼车方式：车辆主动的方式是将乘客请求进行组合后，和车辆进行匹配；乘客主动的方式中，乘客提交拼车请求后，平台为乘客分配车辆。Xu等人［23］提出使用动态规划的方法，将查询最优乘客插入位置的问题转换为查询时间间隔最小值的问题。Birx等人［24］研究了动态场景下多乘客和多车辆的拼车问题，提出了重新规划框架和遗忘框架，并给出解决匹配问题的启发式算法。Xu等人［25］提出了一种基于椭圆约束的方法以提高插队的效率，若乘客请求的起点和终点位置在椭圆内，则可以插入至车辆路线。Ferreira等人［26］将乘客上车和下车位置固定在某一特定的集合，从而提高乘客与车辆之间路线的相似度，过滤掉路线与乘客上下车位置不重叠的车辆。Yang等人［27］在拼车匹配优化模型中引入了匹配范围和等待时间间隔的概念，构建了一种能够显著提高匹配成功率的优化模型。陈玲娟等人［28］研究带时间窗约束的静态拼车问题，从三个方面建立乘客车辆匹配及路径优化的目标函数，采用演化策略算法求解问题。孙芮等人［29］提出了基于订单匹配数量、司机旅行时间、乘客等待时间和乘客延误时间的合乘匹配模型，并设计了对应匹配与路径规划算法。王志建等人［30］以车辆的总行驶距离最短以及总信任度值最高为目标，引入信任度权重和用户偏好来衡量合乘的信任水平，对合乘轨迹线路进行优化。考虑到拼车的实际应用场景，Sun等人［31］基于拼车平台的现实情况，提出平台派单和司机抢单的混合匹配系统，并计算出了系统的最大匹配半径。针对机场拼车，晏鹏宇等人［32］提出前瞻式动态拼车匹配策略，将未来随机到达的乘客信息纳入拼车匹配决策中，建立了乘客匹配与车辆路径联合优化两阶段随机规划模型。在考虑社会效益和服务质量的基础上，袁鹏程等人［33］提出了基于风险分级的多目标拼车模型。

国内外关于订单分配与路径优化的先前研究为本文的研究提供了理论基础。在典型的PDP问题研究中，已经提出了各种各样的拼车模型，但实际拼车服务仍存在一些尚未解决的问题。首先，大多数学者仍然将拼车问题研究限定在静态层面，即为特定状态下的司机和乘客进行匹配和调度，司机只能机械地执行平台分配的订单，在其服务过程中无法接受新的订单。司机完成服务后，平台为其重新派单，这会导致司机等待接单时间延长，降低了系统的派单效率。其次，学者们在动态拼车研究中专注于提高拼车匹配成功率，忽略了插单后司机收益的变化，这可能导致插单后司机服务更多乘客，但其收益比为较少乘客服务时更低，降低了司机的服务热情。因此，与以往的研究不同，本文研究的是一个新的动态插单问题，即在乘客拼车请求实时更新的实际场景下，平台如何综合考虑车辆位置、新的乘客订单以及待服务订单等信息，在服务过程中为司机持续分配一个或多个订单，在保证司机收益提升的基础上，提升整个系统的派单效率。

2 模型构建

2.1 问题描述

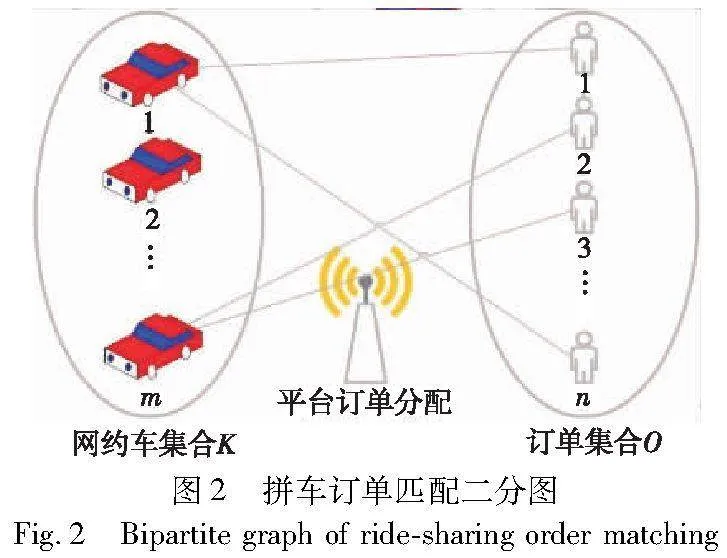
本文研究的是拼车订单匹配与路径优化的实际场景，即如何为仍有未完成订单的拼车服务司机分配一个或多个订单，以最大化司机收益。具体而言，系统中有m位司机，司机k当前已接受了hk个订单待完成，订单池里有n个订单待分配，拼车平台的任务是为每位司机分配一个或多个订单，并重新规划路径，以最大化司机总收益。使用图2展示的二分图来表示这个问题，其中点集K表示提供拼车服务的司机，点集O表示待分配拼车订单，K与O互不相交，且图中的每条边（k，i）所关联的两个顶点k和i分别属于K和O（k in K，i in O）。

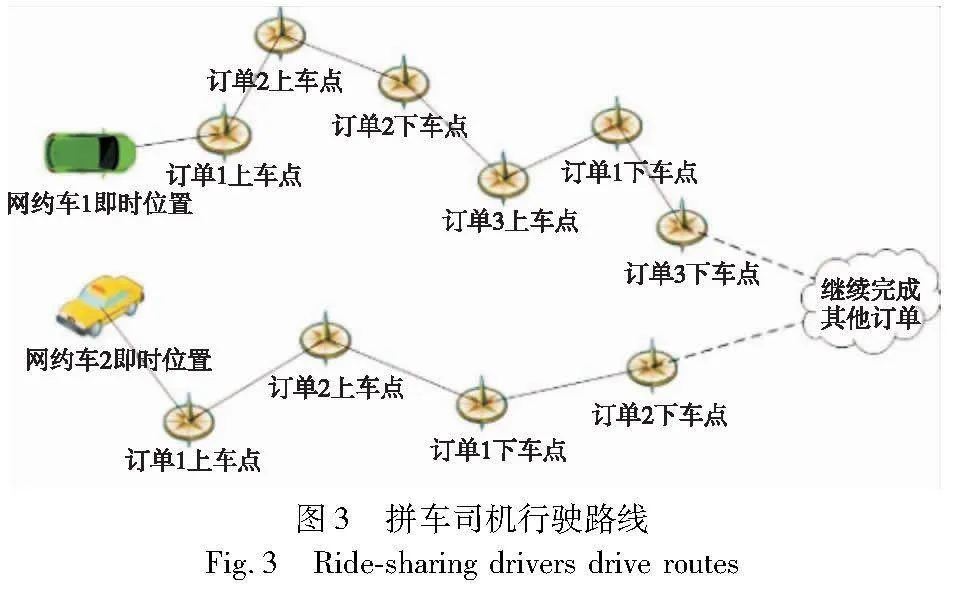
在本文研究的问题中，司机具有灵活性，可以在任意空闲时间开始或停止接单。因此，司机的行驶路线不是闭环，而是从当前位置出发，不断接单继续完成任务，如图3所示。拼车问题具有以下特点：a）每个订单需上车再下车；b）乘客上下车有时间窗，乘客需在上车时间窗内上车，并且若乘客下车时间超出最晚下车窗，对司机有惩罚；c）网约车容量有限，存在乘客数量限制。

2.2 双层规划模型

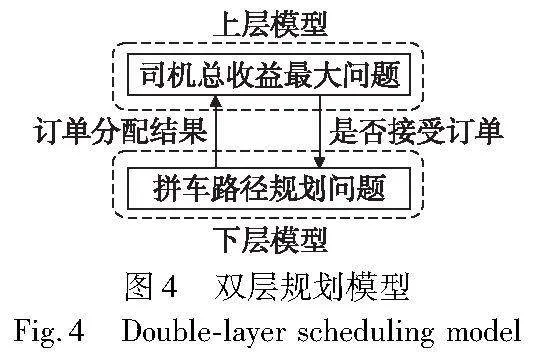
对拼车司机来说，所得收益不仅是每个订单预计收益的简单相加，还需扣除行驶成本，以及因延迟到达终点导致的惩罚成本。因此，在订单分配时还需考虑司机是否能在最晚预计时间内将乘客送达终点、是否会产生惩罚等情况。拼车路径规划本身是NP-hard问题，而订单分配则是基于路径规划的更高层次的决策问题。

本文提出了一个双层模型，如图4所示。其上层模型通过设定的评分机制对待分配订单进行评分，根据评分顺序为司机进行订单分配，以司机总收益最高为目标；下层模型则以每位司机收益最大为目标，考虑时间窗、延迟送达惩罚，以及乘客数量约束等因素。下层模型在得到上层模型给出方案后，按照下层模型的最优目标作出反应，从而对上层模型的目标作进一步的优化。可见，上层模型的目标是双层规划的最终优化目标。

2.2.1 订单评价分配模型

在上层模型中，为司机加入推荐订单的顺序将直接影响最终订单分配的结果。对平台而言，将K个司机与n个订单所有可能的顺序组合，有KAnn种，为了减小求解规模，同时增加较优的订单被分配的可能性，本文先建立订单评分模型。

订单评分模型考虑了订单对司机收入影响的主要因素，包括订单预计收益、订单上车时间、订单需求行驶速度和订单上车点位置。针对这四个主要因素构建评分模型：s（UP）i为订单i的预计收益得分，收益高的订单得分更高；s（TP）i为订单的上车时间得分，订单最早上车时间越早，得分越高；s（VP）i表示订单的预期行驶速度，将上下车点的距离作为司机的预计行驶距离，最早上车时间和最晚下车时间的差值作为预计行驶时间，两者的比值为订单的预期行驶速度，对预期行驶速度要求低的订单，分数更高；s（DP）ki是订单上车点与司机当前位置距离得分，订单上车点距离司机位置越近，该项得分越高。对司机k而言，订单i的评分为

S_Oki=s（UP）i·UW+s（TP）i·TW+s（VP）i·VW+s（DP）ki·DW（1）

其中：UW、TW、VW和DW分别表示各因素所占权重，各项权重之和为1：

UW+TW+VW+DW=1（2）

订单评分模型的决策变量：

S_O表示整个订单匹配结果的评分总和，为所有司机对已分配订单的评分累加，可进一步表示司机总收益最大：

2.2.2 拼车路径规划模型

1）符号说明及模型假设

考虑在拼车服务运营区内，司机k目前已接受了hk个订单但尚未完成，订单池里有n个订单待分配。n为订单总数，O为订单集合，O={1，2，…，i，…，n}；司机起始位置VK0={0}，司机目标终点位置VKT={2n+1}，VS表示乘客上车节点集合，VS={1，2，…，i，…，n}；VE表示乘客下车节点集合，VE={n+1， n+2，…，n+i，…，2n}；V表示所有节点集合，V=Vk0∪VS∪VE∪VKT。

dij为节点i到j的距离；aki为司机k到达节点i的时间；［ei，lsi］为订单i的乘客上车时间窗；lie为订单i最晚到达时间窗；Ii为订单i的预计收益。vk为司机行驶速度；Qk为司机乘客容量；qki为司机k离开节点i时所载乘客数量；qi表示需求点i的乘客数量；ski为司机k离开节点i的时间；wki为司机k在节点i的等待时间；α为行驶成本系数，β为延误惩罚成本系数。

路径规划模型基于以下假设进行：a）在匹配和规划过程中，车辆位置和拼车订单的起止位置已经确定；b）在行驶过程中，禁止司机随意搭乘未参与拼车的乘客；c）位置信息使用两点间的直线距离，车辆匀速在规划路径上行驶，不考虑停启时间、乘客上下车时间及交通拥堵导致的时间延误。

2）数学模型

路径规划模型的决策变量由两部分组成。0-1变量xkij表示司机行驶路线，若司机k由节点i行驶到节点j，则xkij=1，否则，xkij=0；0-1变量zki表示司机k完成订单i时是否出现延误的情况，若出现延误，则zki=1，产生延误惩罚，否则，zki=0。

司机收益为所有被服务乘客支付的拼车费用减去车辆行驶的总消耗以及延误的惩罚成本。路径规划模型的目标函数为司机收益最大，其中第一部分表示所有订单预计收益之和，第二部分表示司机的实际行驶成本，第三部分表示对司机未按时完成订单的惩罚成本，则最大化司机总收益可以写为

式（5）～（14）为相关约束条件。提供拼车服务的司机必须从当前位置出发：

在拼车服务过程中，每个订单的上车点和下车点都必须被访问：

计算车辆k到达节点j的时间，当该节点为起始节点时，到达时间为0；当该节点为非起始节点时，到达时间为司机离开前一节点的时间再加前一节点到本节点的行驶时间：

计算司机在节点i的等待时间：若节点i为下车节点，则司机在该节点无须等待；当节点i为上车节点时，（ei-aki）+表示ei-aki值非负的部分，若司机在乘客上车时间窗起始时间之前到达，即ei>aki，此时（ei-aki）+为ei-aki的值，表示司机需等到乘客上车时间窗起始时间，若司机在乘客上车时间窗起始时间之后到达，即ei＜aki，则该值为0，表示司机在该节点无须等待：

司机离开节点i的时间为司机到达节点i的时间加上司机在节点i的等待时间：

ski=aki+wki i∈V（11）

所有的拼车乘客都必须满足先上车后下车约束：

aki≤akn+i i∈R（12）

计算车辆承载乘客数量：若节点j为起始节点，则此时承载乘客数量为0；若节点j为上车节点，则经过该节点后车辆承载乘客数量为经过上一节点承载乘客数量qki与需求点j的乘客数量qj加和，反之，若节点j为下车节点，则经过该节点后，车辆承载乘客数量为经过上一节点的乘客数量qki与需求点j的乘客数量qj作差：

车辆承载乘客数量不超过最大限制约束：

qkj≤Qk j∈V（14）

3 求解算法

3.1 双层算法逻辑

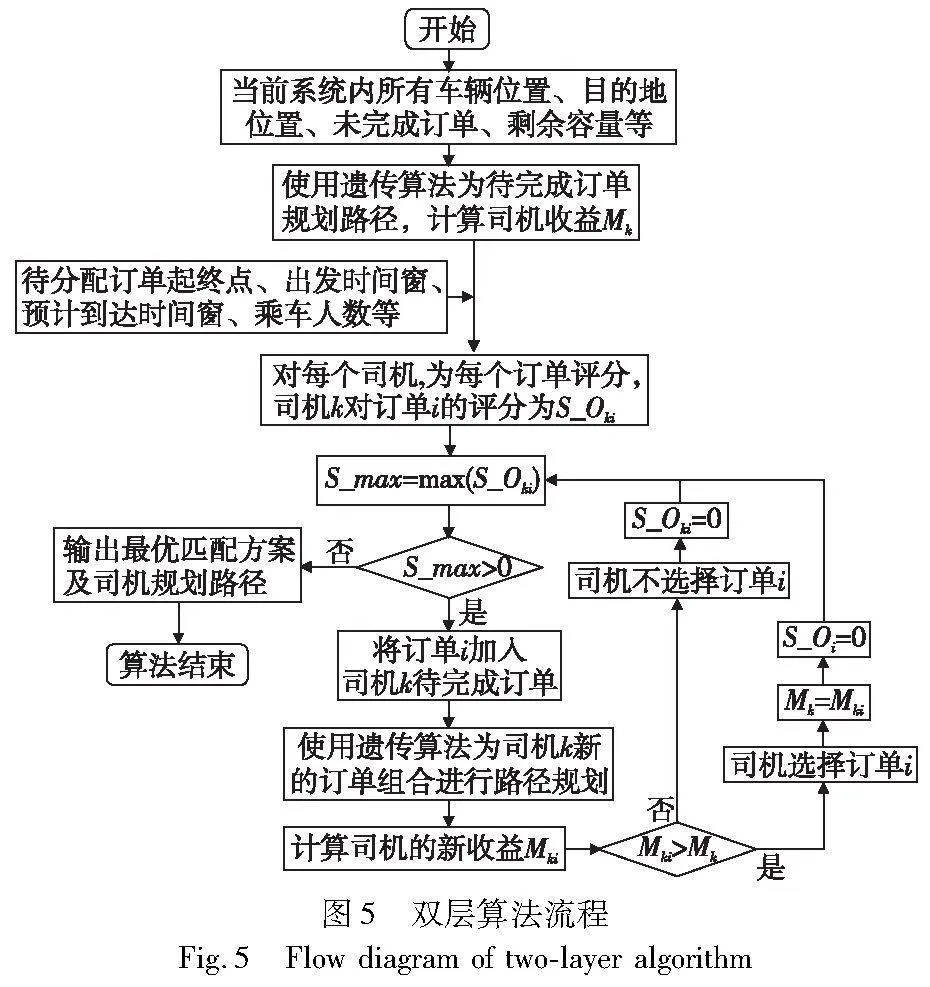
本文提出的双层算法，其上层逻辑采用贪心算法，对实时推荐的订单通过评分机制进行评分，根据不同司机对不同订单的评分结果，按照评分从高到低的顺序为最高得分对应司机分配对应订单，并为该司机进行路径规划。如果加入新订单后的收益大于原有订单所带来的收益，则该司机接受该订单，并将该订单对所有司机的得分都清零；否则该司机不接受该订单，仅将该司机对该订单的得分清零。这个过程持续进行，直到所有司机对所有订单的评分均为零。

下层逻辑为以收益最大为目标，考虑乘客上下车时间窗、延迟到达惩罚、承载乘客数量约束等现实因素，进行路径规划，该问题使用改进的遗传算法进行求解。本文设计的双层算法流程如图5所示。

3.2 贪心算法

贪心算法是当前看来最优的选择，本文采用的贪心策略并不是从整体上加以考虑作出的选择，而只是在某种意义上的局部最优解算法，采取这样的策略是为了提高运行速度。

在本文提出的双层算法中，其上层贪心算法的逻辑即为通过某个评分机制将待分配订单进行评分，由于某一区域内平台实时订单和司机数量均较多，首先基于评分结果向司机推荐分数最高的订单，可以一定程度上提高求解速度。通过下层运算得到司机接受订单后获得的收益，若加入新订单后的收益大于原有订单组合的收益，则接受该订单，否则不接受，直到无法接受任何订单为止。

3.3 改进遗传算法

3.3.1 编码方式

为便于体现上车点与下车点的区别，本文采用自然数编码的方式对两者进行编码，0，1，2，…，2n是2n+1个访问点，其中，0为起点，即司机当前所在位置；1，3，5…，2n-1为上车点，分别对应第1，2，…，n号订单，对应下车点为2，4，6，…，2n，即订单i的上车点编码为2i-1，下车点编码为2i。以一个包含3个未完成订单的情况为例，上车点与下车点的编码如表1所示，起点为0。以上编码组随机排序组合成一条染色体，代表一条行驶路线，如0-1-5-6-3-4-2，其中，每个编码对应染色体上的一个基因。

3.3.2 初始化种群及改进的个体构造方法

由于带有上下车顺序约束以及承载乘客数量约束，随机生成的初始种群符合约束的概率较小，导致遗传算法在后续运算中难以取得良好结果。为了提高初始种群的质量以及算法运算速度，本文提出两个构造方法，在随机生成初始种群的基础上，对不符合约束的染色体重新构造。

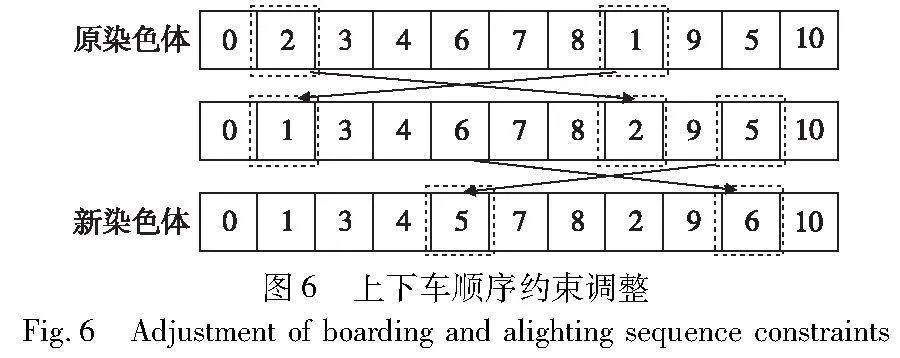
1）上下车顺序约束构造

若随机生成的染色体中存在某个下车点在对应订单的上车点之前访问，则将该订单的下车点与上车点位置对换，同时保持其余访问点位置不变。例如，当前司机共有5个订单，假设随机生成的某一染色体为0-2-3-4-6-7-8-1-9-5-10，其中，1号订单的上车点1出现在对应的下车点2之后，3号订单的上车点5出现在对应的下车点6之后，不符合上下车顺序约束，因此将基因1与2的位置对换，基因5与6的位置对换，其余基因位置保持不变，形成新的染色体，其操作如图6所示。

2）承载乘客数量约束构造

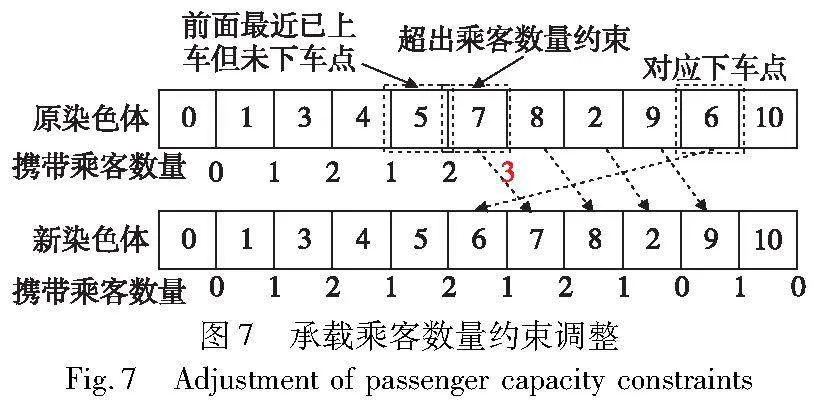
司机访问上车点后，车辆承载乘客数量增加，访问下车点后，承载乘客数量减少。若在访问某点后，车辆承载乘客数量超过容量，那么该点一定为上车点，同时，该上车点前一定有其他尚未下车的订单的上车点。为了避免破坏上下车顺序约束，本文以超出乘客数量约束的点所在的基因位为界限，找到该点前距该点最近的已经上车但尚未下车订单的上车点，再找到该上车点对应的下车点，将该下车点前移至超出乘客数量约束的点所在基因的前一位。

以图7为例，假设车辆承载乘客容量为2，每个订单只有一位乘客。当车辆访问上车点7后，订单数量为3，乘客数量超过了容量限制，需要从上车点7向前寻找已经上车但未下车的订单。显然，点5是距离上车点7最近的上车点，且上车点5对应的订单尚未下车。找到上车点5对应的下车点6，将6移至7前一位，原染色体中5与6之间的基因均依次后移一位，其余基因位置保持不变，形成新的染色体。

经过这样的调整，染色体在满足承载乘客数量约束的同时，也不会违反订单的上下车顺序约束，可以直接得到最终符合约束的可行解。

3.3.3 适应度函数

根据2.2.2节的拼车路径规划模型，目标函数为最大化司机总收益。在改进的遗传算法中，适应度函数为拼车司机服务的收益，可以表示成目标函数max M相同的形式：

其中：三个部分分别表示所有订单预计收益之和、实际行驶成本，以及未按时完成订单的惩罚成本。根据适应度函数，可以计算出初始种群中各个体的适应度值。

3.3.4 遗传算子设计

a）采用轮盘赌方法选择算子。

b）交叉算子采用部分匹配交叉规则（partially mapped crossover，PMX）。随机产生两个随机数，满足0≤k1＜k2≤染色体长度，如k1= 3，k2=6作为截取染色体片段的起始位置，将截取到的两个片段进行位置交换，可得到两个新个体。如图8所示，交叉的基因片段为“4-5-7-8”和“4-1-10-7”，将这两段基因片段在父代染色体中互换，得到新的子代染色体。可见子代1中基因1、基因10重复出现，却缺少基因5、8，子代2中基因5、8均出现两次，却缺少基因1、10，说明交叉得到的染色体很容易不符合约束。

为了解决交叉操作后基因重复的问题，本文的处理是保持被交换的片段不动，在没有交换的片段中寻找重复值，再在交叉部分中找到对应位置的元素进行映射替换，15，1078，至新的子代没有重复基因为止，如图9所示。

c）根据预先设定的变异概率判断父代染色体是否变异，若变异，则随机选择两个基因位置，交换这两个位置的基因，形成新的子代。

d）本文采用精英选择策略进行种群更新，先进行当前种群的交叉和变异，交叉及变异得到的新的子代若不符合约束，同样使用3.3.2节中所述方法将其改造，然后，根据染色体的适应度，从父代和子代群体中筛选出当前适应度最高的染色体，数量满足群体大小，形成新的种群。

3.3.5 遗传终止条件

为了确保算法尽可能接近最优解，同时减少运算时间，采用以下两个迭代终止条件：a）若连续50次迭代的适应度相同，则终止迭代；b）迭代次数达到最高300次，则终止迭代。

4 算例分析

4.1 算例基础数据

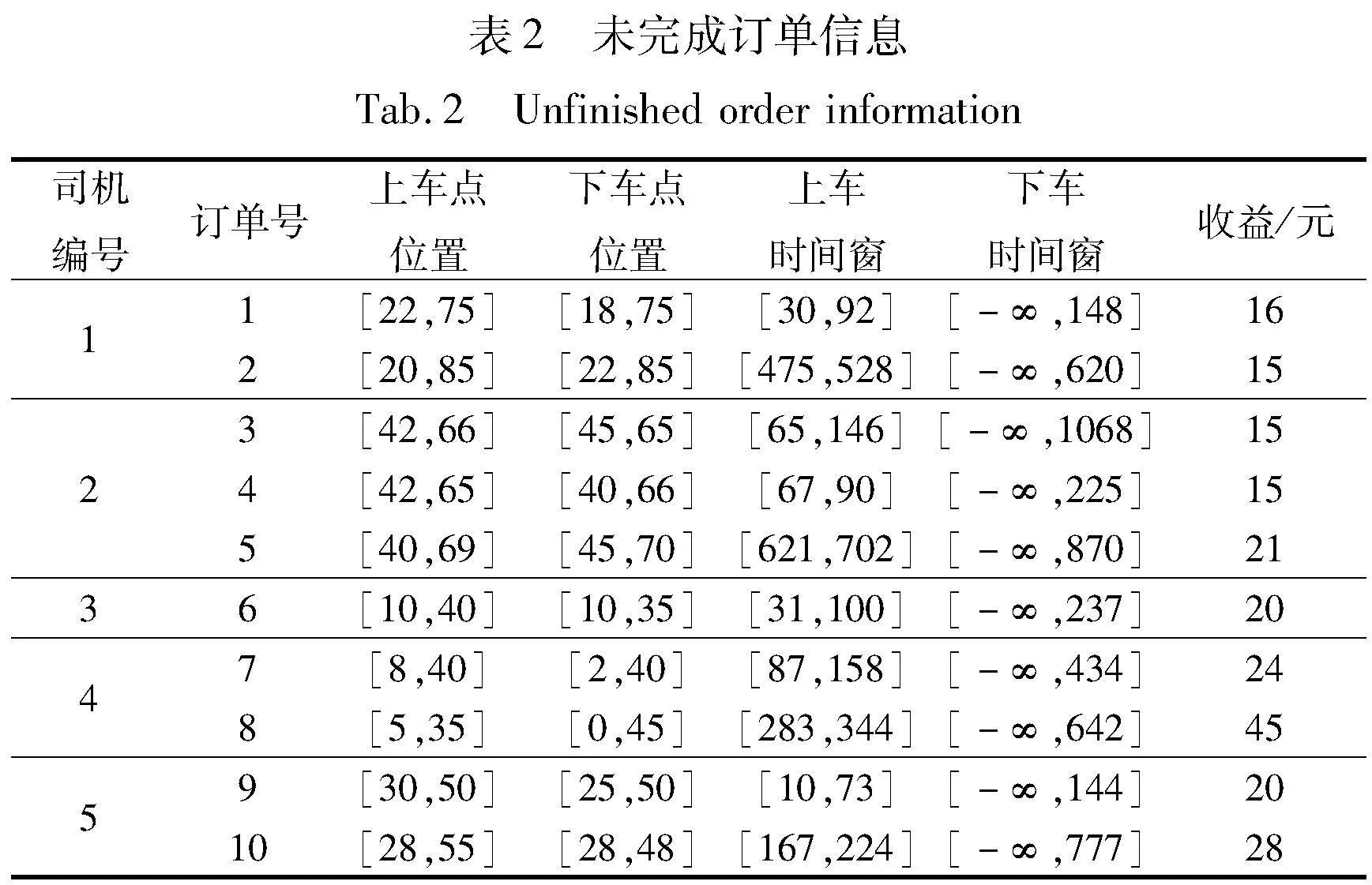
通过一个具体的算例对DMRS-DES模型的有效性进行验证。算例包含5位司机，每位司机均有若干个未完成订单，其各自未完成订单的信息如表2所示。

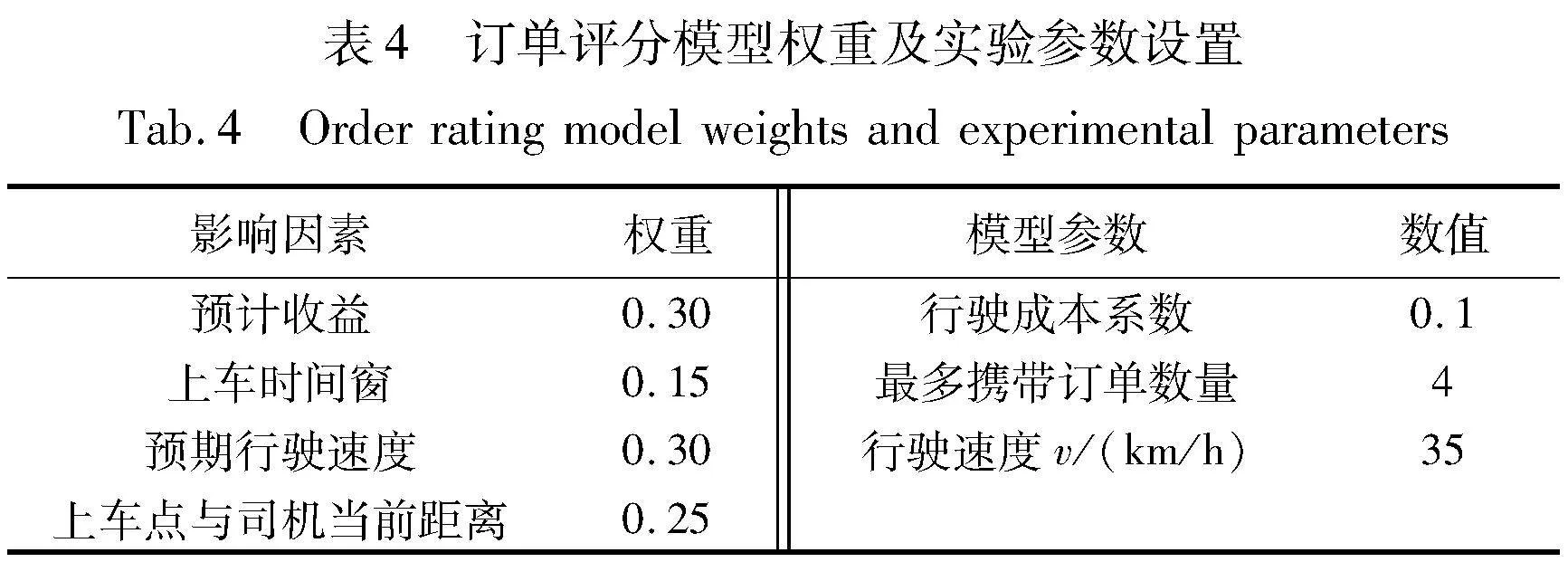
此时，拼车平台根据一定原则，为这些司机推荐了10个新订单，订单信息如表3所示。订单评分模型权重及服务过程车辆的各项参数设置如表4所示，通过订单评分模型得到司机对应各个订单的百分制分数如表5所示。

4.2 算例实验结果

本文利用MATLAB R2022a进行编程求解，所有数据均在AMD Ryzen 7 3700U with Radeon Vega Mobile Gfx2.30 GHz配置的计算机上进行仿真实验。遗传算法的参数设定为种群大小=60，交叉概率=0.9，变异概率=0.05。

当前待完成订单的路径规划结果如表6所示，通过计算得出了每位司机的最优行驶路线、预计收益、延误时间及行驶距离。

在现有订单基础上，利用设计的双层算法，从10个推荐订单中为司机分配合适的订单。由于现实拼车调度问题的特点，求解模型的速度和决策难度的提高成为重要的考虑因素。为了验证算法的计算速度，进行50次实验，对程序运行时间进行统计，如图10所示。50次实验的程序运行时间均在5～8 s，仅有4次实验的程序运行时间超过了7 s。程序运行平均时间为6.45 s，证明对10个推荐订单的分配花费时间可接受。

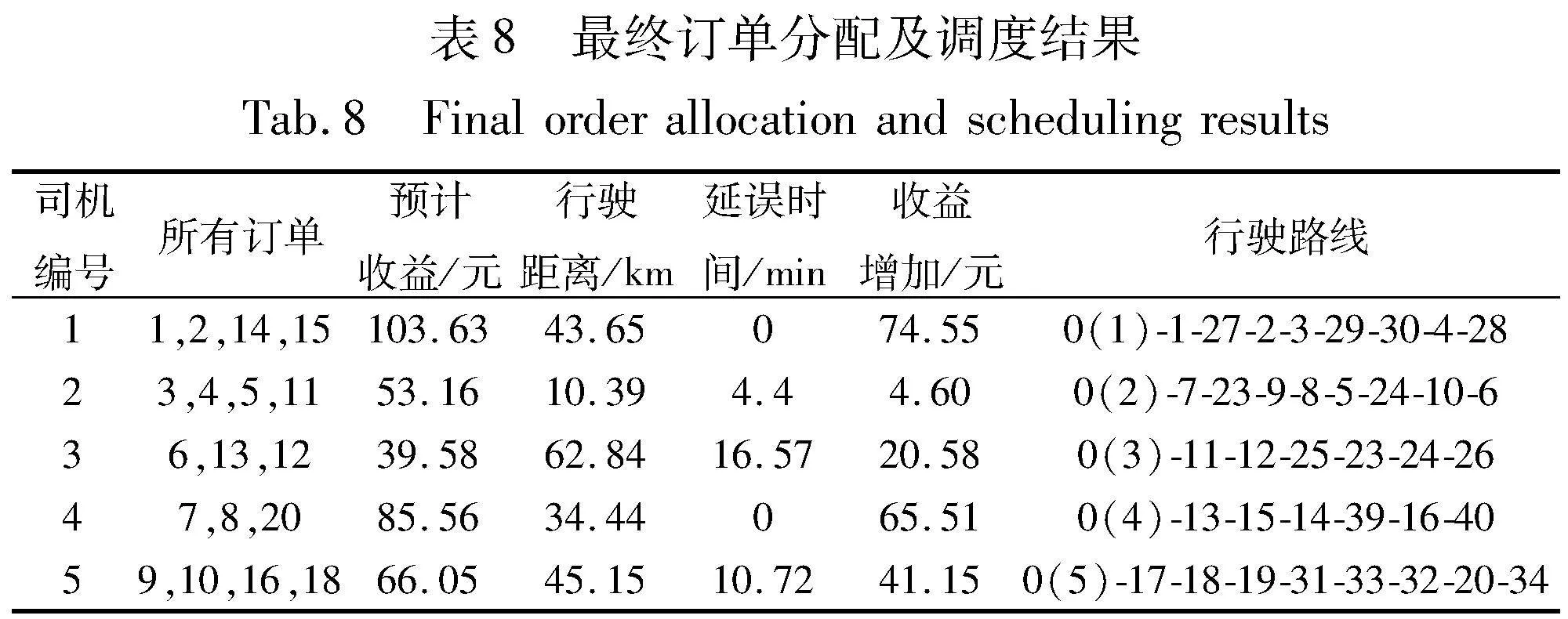
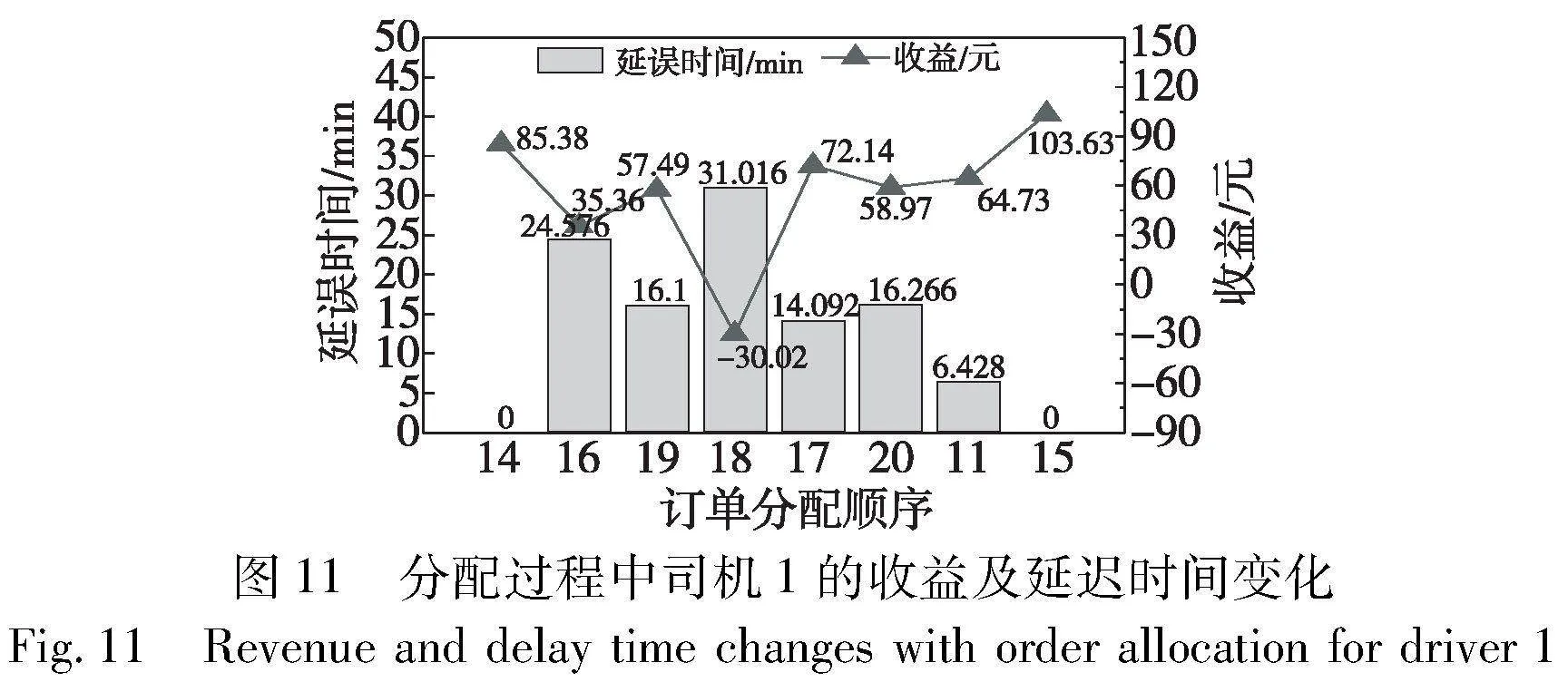
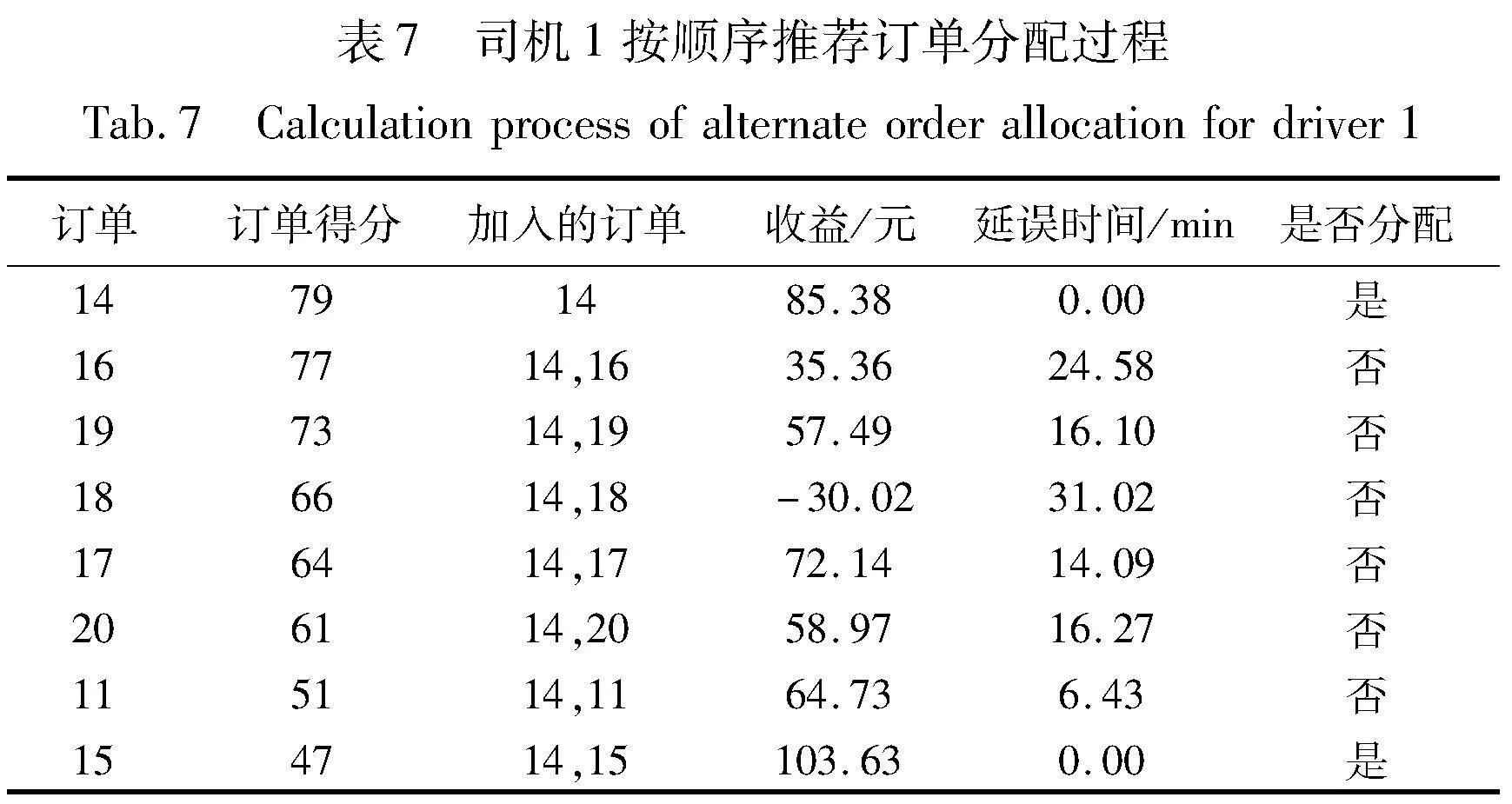
表7和图11以司机1为例，更直观地展现了按照本文提出的双层算法为司机分配订单后，其预计收益的变化。可以看出，并非订单数量越多收益越大，若多个订单的下车时间窗过近或距离过远，过多的订单将导致送达时间延迟产生惩罚，进而降低收益。还需注意的是，初始的订单评分越高只是表示“优先考虑”但并非“最终选择”，如对司机1而言，虽然订单16的评分为77，而订单15的评分仅为51，根据评分顺序模型，优先考虑了订单16，但并没有直接分配给司机1，最终仅为其分配了订单14与订单15，这种情况发生的原因是加入订单16后的收益小于仅分配订单14的收益。

表8展示了总收益最优的订单分配结果。系统提供的10个订单中，有8个订单分别分配给几位司机。而对于订单13和17而言，无论分配给哪位司机，均会使其收益减少，进而减少系统的总收益。以司机1为例，为其分配订单14和15后，其收益达到了103.63元，增加了84.43元，并且可以在没有延误的情况下完成两个待完成订单和两个新分配的订单。将其行驶路线染色体翻译成最终结果为：司机1当前位置→订单1上车→订单14上车→订单1下车→订单2上车→订单15上车→订单15下车→订单2下车→订单14下车。

为了评估在考虑司机仍有未完成订单的状态下，DMRS-DES模型的调度效果，本文将采取随机策略分配订单，按最近上车点距离策略分配订单，将其收益和延误时间与本模型进行对比，对比结果如表9所示。

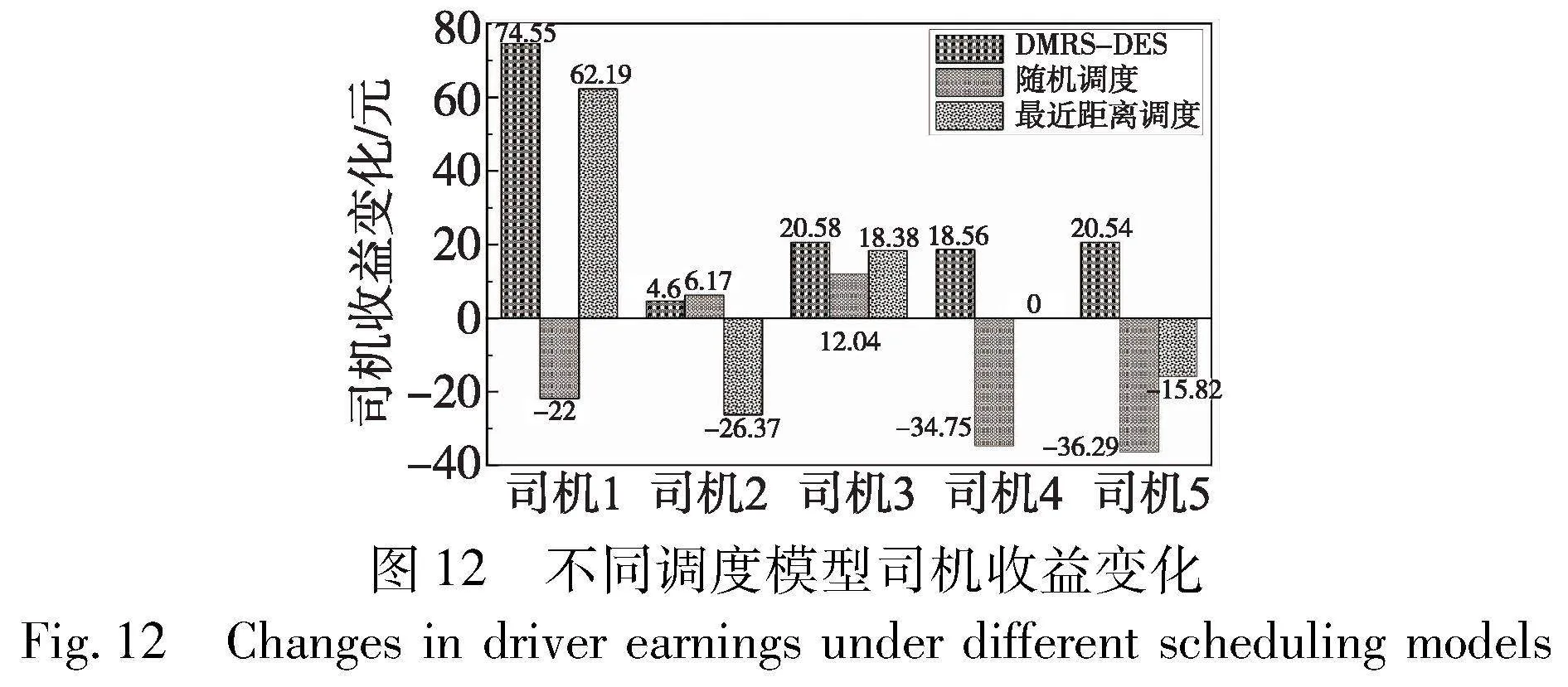
仿真模型输出结果主要包括司机行驶距离、延误时间和司机的收益变化三个参数。通过表9可以看到，采用不同的调度模型对司机的收益影响较大。以司机4为例，采用本模型为其在原有两个未完成订单的基础上再分配订单20，通过模型规划的路线，预计其收益增加18.56元，且无延误；若采取最近距离调度模型，由于系统推荐的10个订单都离司机4较远，则不会给司机4分配新的订单，其收益不变；若采用随机分配模型，则为其分配订单17和18，则其预期收益降低34.75元，且延误时间高达46.65 min。对实验结果进行整体分析，本文模型在司机整体收益变化、行驶距离和延误时间三个方面均显著优于随机调度模型和最近距离调度模型，说明DMRS-DES模型在最大化所有司机整体收益的同时，也可以较好地降低总行驶距离，减少延误时间。

通过图12可以看出，匹配成功的订单数量增加，并不一定会导致司机收益的相应增长。若多个订单的下车时间窗相近，将过多的订单分配给司机可能会引起送达乘客的延迟，进而产生相应的惩罚，降低司机的收益。

图13分别展示了不同的调度模型对总行驶距离及延误时间的影响，可以看出，本文提出的调度模型在保证收益提升的前提下，相比较于其他模型也降低了行驶成本和延误损失。DMRS-DES模型中未分配的订单保留在订单池内，可以在后续的调度循环中再进入订单组合，进行进一步优化，这与实际情况相符，即拼车订单并不一定会在被推荐后短时间内被司机接受。

5 结束语

本文根据拼车平台调度的特点，提出DMRS-DES模型为拼车平台订单分配及路径规划提供决策参考。该模型中遵循为司机分配新订单要保证其收益增加的基本原则，同时综合考虑行驶成本及延误惩罚，以实现收益最大化。本文设计了对应的双层算法，将订单分配与路径规划同时进行计算，先基于订单评分决定进入订单分配的次序，再进行下层的路径规划，决定是否分配该订单，路径规划允许订单交叉执行。在求解下层的路径规划模型中，本文设计了改进的遗传算法，进行染色体的重新构造，使染色体满足拼车的上下车顺序及承载乘客数量约束。

通过MATLAB进行算例分析，验证了模型与算法在小规模问题下的求解效果与速度。通过与随机分配调度模型与最近距离调度模型进行对比，验证了算法的有效性。结果表明，在拼车司机仍有未完成订单的实际应用场景中，应用本文模型进行订单分配能增加司机收益，同时减少总行驶距离与延误时间。

在后续研究中，对仍有未完成订单的司机如何进行拼车订单和独享订单的联合调度问题，可以作为进一步探讨的方向。本文的研究成果可以扩展到更大规模的问题，当拼车平台面对的司机和乘客数量更多时，其订单分配方式的组合数量会呈指数增长，参考本文提出的评分方法进行订单的初始筛选和排序，可以有效降低求解时间。

参考文献：

［1］Benjaafar S， Bernhard H， Courcoubetis C. Drivers， riders and ser-vice providers： the impact of the sharing economy on mobility［C］//Proc of the 12th Workshop on Economics of Networks， Systems and Computation. New York：ACM Press， 2017： 1-6.

［2］Benjaafar S， Hu Ming. Operations management in the age of the sharing economy： What is old and what is new？［J］. Manufacturing & Service Operations Management， 2020，22（1）： 93-101.

［3］Wang Jingpeng， Huang Haijun. Operations on an on-demand ride service system with express and limousine［J］. Transportation Research Part B： Methodological， 2022，155： 348-373.

［4］Tirachini A. Ride-hailing， travel behaviour and sustainable mobility： an international review［J］. Transportation， 2020，47（4）： 2011-2047.

［5］Standing C， Standing S， Biermann S. The implications of the sharing economy for transport［J］. Transport Reviews， 2019，39（2）： 226-242.

［6］Si Hongyun， Duan Xu， Cheng Long， et al. Determinants of consu-mers’coni79WNU47wt8ICws6Amn0+Q==tinuance intention to use dynamic ride-sharing services［J］. Transportation Research Part D： Transport and Environment， 2022，104： 103201.

［7］Wang Xing， Agatz N， Erera A. Stable matching for dynamic ride-sharing systems［J］. Transportation Science， 2018，52（4）： 850-867.

［8］徐毅， 童咏昕， 李未. 大规模拼车算法研究进展［J］. 计算机研究与发展， 2020， 57（1）： 32-52. （Xu Yi， Tong Yongxin， Li Wei. Recent progress in large-scale ridesharing algorithms［J］. Journal of Computer Research and Development， 2020，57（1）： 32-52.）

［9］Qian Xinwu， Zhang Wenbo， Ukkusuri S V， et al. Optimal assignment and incentive design in the taxi group ride problem［J］. Transportation Research Part B： Methodological， 2017，103： 208-226.

［10］Vazifeh M M， Santi P， Resta G， et al. Addressing the minimum fleet problem in on-demand urban mobility［J］. Nature， 2018，557（7706）： 534-538.

［11］Tang Xiaocheng， Qin Zhiwei， Zhang Fan， et al. A deep value-network based approach for multi-driver order dispatching［C］//Proc of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining.New York：ACM Press， 2019： 1780-1790.

［12］吴玥琳， 袁振洲， 陈秋芳， 等. 考虑轨迹相似度的综合客运枢纽出租车合乘方法研究［J］. 交通运输系统工程与信息， 2020，20（2）： 188-195. （Wu Yuelin， Yuan Zhenzhou， Chen Qiufang， et al. Taxi pooling method of urban integrated passenger transport hub with trajectory similarity［J］. Journal of Transportation Systems Engineering and Information Technology， 2020，20（2）： 188-195.）

［13］Kucharski R， Cats O. Exact matching of attractive shared rides （ExMAS） for system-wide strategic evaluations［J］. Transportation Research Part B： Methodological， 2020，139： 285-310.

［14］De Palma A， Javaudin L， Stokkink P， et al. Ride-sharing with inflexible drivers in the Paris metropolitan area［M］//Transportation.Berlin：Springer， 2022： 1-24.

［15］Atasagun G C， Karaogˇlan I·. A mathematical model for the time dependent vehicle routing problem with simultaneous pick-up and deli-very［J］. Journal of the Faculty of Engineering and Architecture of Gazi University， 2019，34（4）： 1743-1755.

［16］Masoud N， Jayakrishnan R. A real-time algorithm to solve the peer-to-peer ride-matching problem in a flexible ridesharing system［J］. Transportation Research Part B： Methodological， 2017，106： 218-236.

［17］郭羽含， 伊鹏. 长期车辆合乘问题的复合变邻域搜索算法［J］. 计算机应用， 2018，38（10）： 3036-3041，3052. （Guo Yuhan， Yi Peng. Hybrid variable neighborhood search algorithm for long-term carpooling problem［J］. Journal of Computer Applications， 2018，38（10）： 3036-3041，3052.）

［18］Xu Zhe， Li Zhixin， Guan Qingwen， et al. Large-scale order dispatch in on-demand ride-hailing platforms： a learning and planning approach［C］//Proc of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining.New York：ACM Press， 2018： 905-913.

［19］Hou Liwen， Li Dong， Zhang Dali. Ride-matching and routing optimisation： models and a large neighbourhood search heuristic［J］. Transportation Research Part E： Logistics and Transportation Review， 2018，118： 143-162.

［20］Braverman A， Dai J G， Liu Xin， et al. Empty-car routing in ridesharing systems［J］. Operations Research， 2019， 67（5）： 1437-1452.

［21］Chen Wenyi， Mes M， Schutten M， et al. A ride-sharing problem with meeting points and return restrictions［J］. Transportation Science， 2019，53（2）： 401-426.

［22］Simonetto A， Monteil J， Gambella C. Real-time city-scale ridesharing via linear assignment problems［J］. Transportation Research Part C： Emerging Technologies， 2019，101： 208-232.

［23］Xu Yi， Tong Yongxin， Shi Yexuan， et al. An efficient insertion ope-rator in dynamic ridesharing services［J］. IEEE Trans on Know-ledge and Data Engineering， 2020，34（8）： 3583-3596.

［24］Birx A， Disser Y. Tight analysis of the smartstart algorithm for online dial-a-ride on the line［J］. SIAM Journal on Discrete Mathema-tics， 2020，34（2）： 1409-1443.

［25］Xu Yixin， Kulik L， Borovica-Gajic R， et al. Highly efficient and scalable multi-hop ride-sharing［C］//Proc of the 28th International Conference on Advances in Geographic Information Systems. New York：ACM Press， 2020： 215-226.

［26］Ferreira D L， Nunes B A A， Campos C A V， et al. A deep learning approach for identifying user communities based on geographical pre-ferences and its applications to urban and environmental planning［J］. ACM Trans on Spatial Algorithms and Systems， 2020，6（3）： 1-24.

［27］Yang Hai， Qin Xiaoran， Ke Jieping， et al. Optimizing matching time interval and matching radius in on-demand ride-sourcing markets［J］. Transportation Research Part B： Methodological， 2020，131： 84-105.

［28］陈玲娟， 寇思佳， 柳祖鹏. 网约拼车出行的乘客车辆匹配及路径优化［J］. 计算机与现代化， 2021（7）： 6-11. （Chen Lingjuan， Kou Sijia， Liu Zupeng. Passenger-vehicle matching and route optimization of network carpooling［J］. Computer and Modernization， 2021（7）： 6-11.）

［29］孙芮， 吴文祥. 基于分解算法的动态大规模合乘匹配-路径规划［J］. 科学技术与工程， 2022，22（4）： 1662-1668. （Sun Rui， Wu Wenxiang. Dynamic large-scale ride-matching and route planning based on decomposition algorithm［J］. Science Technology and Engineering， 2022，39（11）： 3351-3357.）

［30］王志建， 郭健， 张强. 考虑乘客信任程度的营运车辆合乘线路规划［J］. 计算机应用研究， 2023，40（4）： 996-999. （Wang Zhijian， Guo Jian， Zhang Qiang. Planning of ride-sharing routes for operating vehicles considering degree of passenger trust［J］. Application Research of Computers， 20EXf6P9V/rwSx0tUAz4bNXQ==23，40（4）： 996-999.）

［31］Sun Luoyi， Teunter R H， Hua Guowei， et al. Taxi-hailing platforms： inform or assign drivers？［J］. Transportation Research Part B： Methodological， 2020，142： 197-212.

［32］晏鹏宇， 张逸冰， 殷允强. 乘客到达时间不确定的机场动态拼车策略与算法研究［J］. 运筹与管理， 2022， 31（8）： 129-136. （Yan Pengyu， Zhang Yibing， Yin Yunqiang. Dynamic matching and vehicle routing approach for airport online ride-sharing services considering uncertainty of passenger arrival times［J］. Operations Research and Management Science， 2022， 31（8）： 129-136.）

［33］袁鹏程， 林徐勋， 韩印. 考虑疫情扩散传播风险的多目标拼车应急管理优化调度模型［J］. 计算机应用研究， 2022， 39（11）： 3351-3357. （Yuan Pengcheng， Lin Xuxun， Han Yin. Multi-objective optimal ridesplitting scheduling model considering risk of epidemic spread［J］. Application Research of Computers， 2022，39（11）： 3351-3357.）