面向动态三维迷宫的综合奖励设计

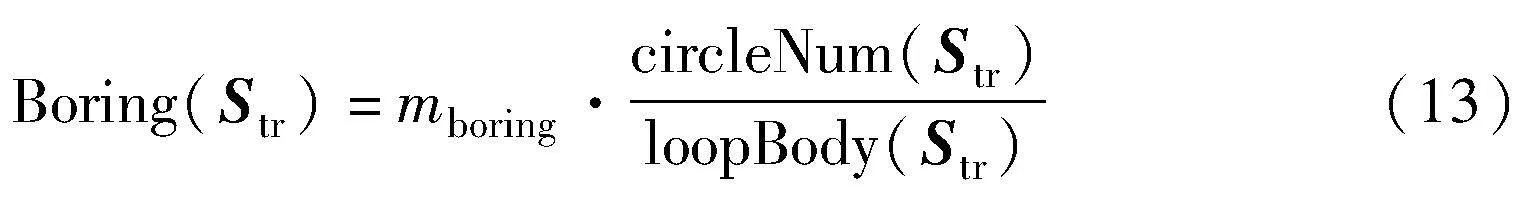
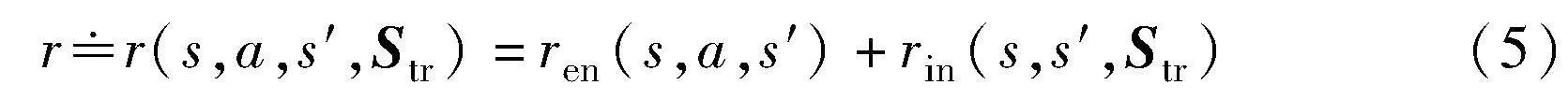



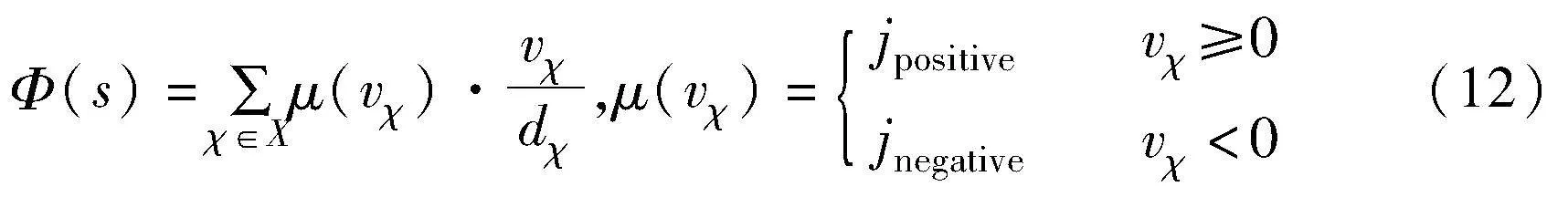


摘 要:动态三维迷宫是较为困难的、具有不确定性和不完全信息的强化学习任务环境,使用常规奖励函数在此环境中训练任务,速度缓慢甚至可能无法完成。为解决利用强化学习在动态迷宫中寻找多目标的问题,提出一种基于事件触发的综合奖励方案。该方案将三维迷宫中各种行为状态表达为各种事件,再由事件驱动奖励。奖励分为环境奖励和内部奖励,其中环境奖励与三维迷宫任务直接相关,含有体现任务目标的节点奖励和任务约束的约束奖励。内部奖励与智能体学习过程中的状态感受相关,含有判断奖励和心情奖励。在实验中,综合奖励的性能均值相较于改进奖励提升54.66%。结果表明,综合奖励方案在提高完成任务满意度、增强探索能力、提升训练效率方面具有优势。
关键词:三维迷宫;奖励设计;强化学习;事件触发
中图分类号:TP391 文献标志码:A文章编号:1001-3695(2024)06-014-1699-05
doi: 10.19734/j.issn.1001-3695.2023.10.0440
Integrated reward design for dynamic 3D mazes
Abstract:Dynamic 3D mazes present more challenging environments for reinforcement learning due to their uncertainty and incomplete information. Conventional reward functions can lead to slow and ineffective task training. This paper proposed an event-triggered integrated rewards scheme to solve the problem of finding multiple targets in a dynamic maze using reinforcement learning. The scheme expressed the various behavioral states in the 3D maze as events, which in turn derived the rewards. This paper divided rewards into environmental rewards and internal rewards. Environmental rewards directly related to the 3D maze mission and included node rewards reflecting the mission objectives and constraint rewards reflecting the mission constraints. Internal rewards linked to the agent’s emotional state during the learning process and encompassed both judgement and mood rewards. The average performance of the integrated reward shows a 54.66% improvement compared to the upgraded reward. The results suggest that the integrated reward scheme offers benefits by increasing satisfaction with task completion, promoting exploration, and boosting training efficiency.
Key words:3D maze; reward design; reinforcement learning; event trigger
0 引言
迷宫问题是一种用于最短路径、最优路径、避障算法等研究的较佳环境载体,目前人工智能的发展使得强化学习成为解决迷宫这类问题的可选智能方案。部分复杂人工智能应用场景研究中,如无人机路径规划、目标跟踪、机械臂避障等,可以简化为动态三维迷宫问题。动态三维迷宫问题的求解环境从二维转为三维,解空间急剧增大,同时由于迷宫中部分路径障碍从静态转为动态,使得智能体的每一步选择具有一定的时空局限性。面对复杂强化学习问题,Dewey[1]认为激发智能体期望行为的奖励设计变得更加困难但更重要,因此如何合理设计奖励函数,成为使用强化学习解决动态三维迷宫问题的关键。
不确定性和奖励稀疏是复杂强化学习问题中出现学习缓慢、探索困境的重要原因,文献[2]介绍了基于不确定性的深度强化学习探索方法,研究使用不同的思路提升探索效率,但是这些方法在复杂强化学习环境的泛化使用仍是一个挑战。奖励设计研究有助于解决奖励稀疏问题,基于势函数的奖励塑造通过先验信息对状态进行先验判断[3],提供了密集化的奖励,成为促进学习过程的启发式奖励设计主流方法,然而先验信息可用性与具体域、场景相关[4],降低了方法的通用性。Wiewiora等人[5]在基于势函数的奖励塑造基础上,将势函数从状态扩展到状态和动作,提出前瞻和回溯两种建议方法,具有一定的启迪性。Cai等人[6]为解决强化学习应用于实际任务的安全问题,提出的新方法在奖励塑造中结合了安全机制,克服奖励稀疏问题的同时保持了安全探索,可惜策略级别的安全值设计也限制了方法的迁移性。内在动机(intrinsic motivation)可以提供与任务无关的一般化探索策略。Singh等人[7,8]引入内在动机,在生物进化问题中通过分析数据,发现该问题的最佳奖励由两部分组成,即外部的任务动机奖励和内在动机的激励探索奖励,但该研究局限于生物进化类任务,对迁移学习尤其是多任务学习的意义还有待探索。Ren等人[9]为解决主要奖励与辅助奖励的平衡问题,以帕雷托最优解(Pareto optimal solution)的形式提出奖励平衡迭代学习框架,相较于启发式奖励设计,有效平衡了奖励关系,然而该框架是否可应用于具有大状态和动作空间的任务仍是一个开放性的问题。近年来,对奖励函数的研究[10~16]集中在范式结构方面,奖励设计的研究大多与特定任务深度绑定[17~20],复杂强化学习问题的通用奖励设计仍是一个挑战。
上述文献对三维迷宫的奖励设计都有一定的参考,但因为依赖各自特定的任务场景,无法直接迁移到三维迷宫强化学习环境中。受以上研究中的各种奖励设计方案启发,本文提出一种新的奖励设计思路:综合环境奖励与内部奖励,设计基于事件触发机制的奖励函数。该思路在三维迷宫中分析出复杂环境中的各种事件,在事件触发的基础上,综合考虑奖励塑造与外在环境以及内在动机的关系,提出奖励函数由环境奖励和内部奖励构成。环境奖励依赖于三维迷宫环境任务动机,内部奖励与智能体系统状态联系紧密,由此共同引导强化学习解决动态三维迷宫问题。
1 融合强化学习的动态三维迷宫环境
1.1 动态迷宫环境及其事件集
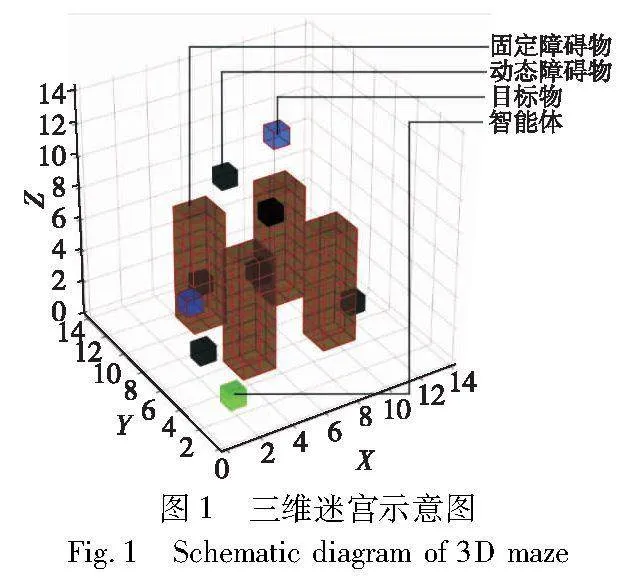
本文给出的动态三维迷宫,如图1所示,它是一个封闭的14×14×14三维格状空间。该迷宫环境包含固定障碍物(wall)、动态障碍物(animal)、目标物(target)和智能体(agent)四类实体,下文中使用括号内的英文时特指迷宫环境中的实体。该环境中agent的任务描述为:在固定步数条件下尽可能少碰撞障碍物、尽可能多到达target位置。其中在到达target位置后,该target将出现在其他位置,环境中始终存在2个target。三维迷宫中有多个实体类型,部分实体位置可以动态变化,是一个非常复杂的强化学习环境,为描述环境变化和设计奖励,提出一种基于事件触发的机制。所有基础事件如表1所示。
根据事件对任务有无直接影响,把基础事件集B划分出奖励集G。B包含了表1中的所有基础事件,G是B一个子集,只包含能够直接影响任务的事件,定义G中元素e3、e5、e6、e7为可触发的节点事件。事件集定义如下:
B={e1,e2,e3,e4,e5,e6,e7,e8}G={e3,e5,e6,e7}
1.2 动态迷宫的强化学习与事件触发机制基础
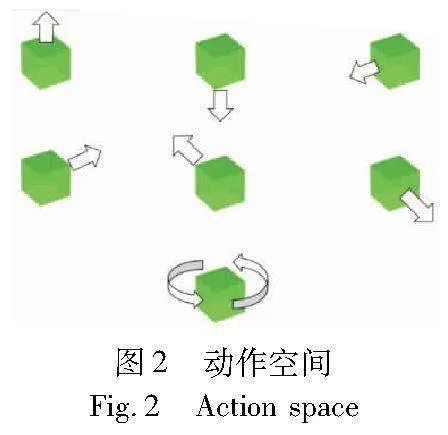
A={up,down,left,right,forward,back,wait}(1)
式(1)是agent动作空间定义,动作集合中的元素分别表示上下左右前后移动一格,wait也视为一种动作,表示原地等待。图2是其示意图。
三维迷宫中的状态信息庞杂,为了能高效获取强化学习的信息元素,agent仅获取合理且有限的环境信息。采用如下形式表示agent可获得的当前状态信息:
s=(x,y,z,vU,dU,vD,dD,vL,dL,vR,dR,vF,dF,vB,dB)(2)
其中:状态前三项(x,y,z)是位置信息,表示当前agent的位置坐标;后续项是观测信息,变量v表示agent碰撞某方向最近实体的预测奖励,变量d表示某方向最近实体与agent当前位置的距离,变量下标中的大写字母表示方向,方向集合X={U,D,L,R,F,B}中的元素是迷宫六个方向的简称,例如vU代表agent从当前位置到达“上”方向最近实体的预测奖励,根据实体与任务的关系,预测奖励值可以根据需要改变。所有状态组合形成状态空间S。
ETrigger(s,a,s′)a∈A,s∈S,s′∈S(3)
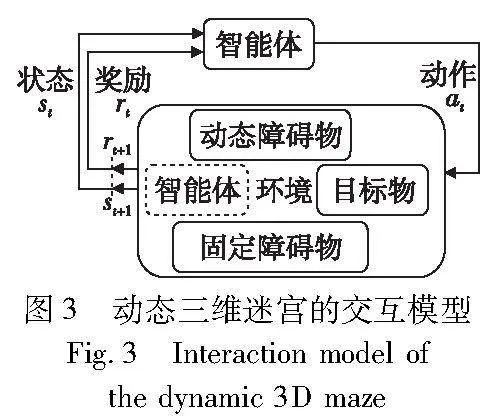
迷宫中事件触发机制由触发函数完成,式(3)中Trigger(·)是事件触发函数,可记录各事件及其触发次数。参数a是智能体采取的动作,s和s′是动作前后的状态。返回值E是集合,包含所有该次触发中获得的事件。动态迷宫任务使用离散时间,t=0,1,2,3,…。将其抽象为强化学习形式,如图3所示。
t时刻智能体获得状态信息st,选择一个动作at,执行后进入新状态st+1,并通过计算得到综合奖励rt。动作与状态的具体设计是强化学习奖励设计的基础,事件集中的各种事件及其触发次数对智能体每一个动作之后状态获取的奖励有很大影响,如表2所示。
在奖励过程中,综合奖励的计算需要利用状态和动作的具体设计并结合事件对奖励的影响和事件触发机制完成,综合奖励的设计影响三维迷宫任务的解决效率,是本文设计中的重中之重。
2 动态三维迷宫的综合奖励函数设计
2.1 动态三维迷宫的任务目标和综合奖励
动态三维迷宫的任务是“在固定步数条件下尽可能少碰撞障碍物、尽可能多到达target位置”,任务的核心在于奖励集的节点事件,因此不宜直接以奖励值评估奖励设计的性能。本文使用成就值作为完成任务性能的主要评价指标。
成就值定义为该轮任务中节点事件奖励re与其次数Ne乘积的累积和,如式(4)所示,事件触发次数Ne可由式(3)获得,奖励值re已知,其直观表示触发节点事件时agent的即时奖励。综合奖励设计中的状态与传统状态意义不同。对较复杂的实际任务,信息完备的理想状态信息很难获得,如无人机的传感器不能直接获取环境完备信息。为去除冗余信息,在动态迷宫中,状态设计为式(2)中非全感知的形式。综合奖励r定义为环境奖励与内部奖励之和:
其中:ren(·)表示环境奖励;rin(·)表示内部奖励;t维向量状态迹Str表示从初始状态s0到当前状态st的状态序列。
Str=(s0,s1,…,st)(6)
环境奖励ren源于传统稀疏奖励设计思想;内部奖励rin包含衡量智能体进步的判断奖励和改善智能体表现的心情奖励,其中心情奖励需要参数状态迹。
2.2 动态三维迷宫综合奖励中的环境奖励
环境奖励表现为当前任务条件下针对三维迷宫环境的客观奖励,受节点事件和任务约束影响,可以细分为节点奖励和约束奖励,如式(7)所示。
ren(s,a,s′)=Reward(s,a,s′)+Penaltyt(Penaltyt-1,s,a,s′)(7)
其中:Reward(·)函数代表节点奖励,是传统稀疏奖励设计的直接扩展;惩罚函数Penalty(·)体现任务约束,补充节点奖励未涉及的部分,使用负奖励描述当前时刻的紧急程度。节点奖励如式(8)所示。
其中:Penaltyt<0,以鼓励agent到达target位置和避免碰撞障碍物;P(·)是中间变量;pei是改变紧急程度的变化参数;pmin是函数的取值下限;pbas是函数的初始值。pmin和pbas取值为(-∞,0)。有利于任务的事件会削弱紧急程度,对应pe取值为(0,1);不利于任务的事件则会增加紧急程度,对应pe取值为(1,+∞);而其他情况则紧急程度不变,取值为1。
2.3 动态三维迷宫综合奖励中的内部奖励
动态三维迷宫的内部奖励是智能体自发产生的主观奖励,由内部系统结合外部环境决定,包括判断奖励和心情奖励。
rin(s,s′,Str)=Judge(s,s′)+Boring(Str)(10)
式(10)中判断奖励由函数Judge(·)实现,该函数使用奖励塑造势函数的概念。心情奖励是agent内部奖励的另一重要部分,负责调控智能体行为以提升算法性能,为避免循环解,使用Boring(·)函数,其思想是给予最近重复行为负奖励,心情奖励可以进行扩充。
Judge(s,s′)=Φ(s′)-Φ(s)(11)
式(11)是判断奖励。Judge(·)函数值为新旧状态势函数的差值,表示对完成任务进步程度的判断;Φ(·)是状态势函数,由agent根据状态进行动态感知。势函数的设计如下:
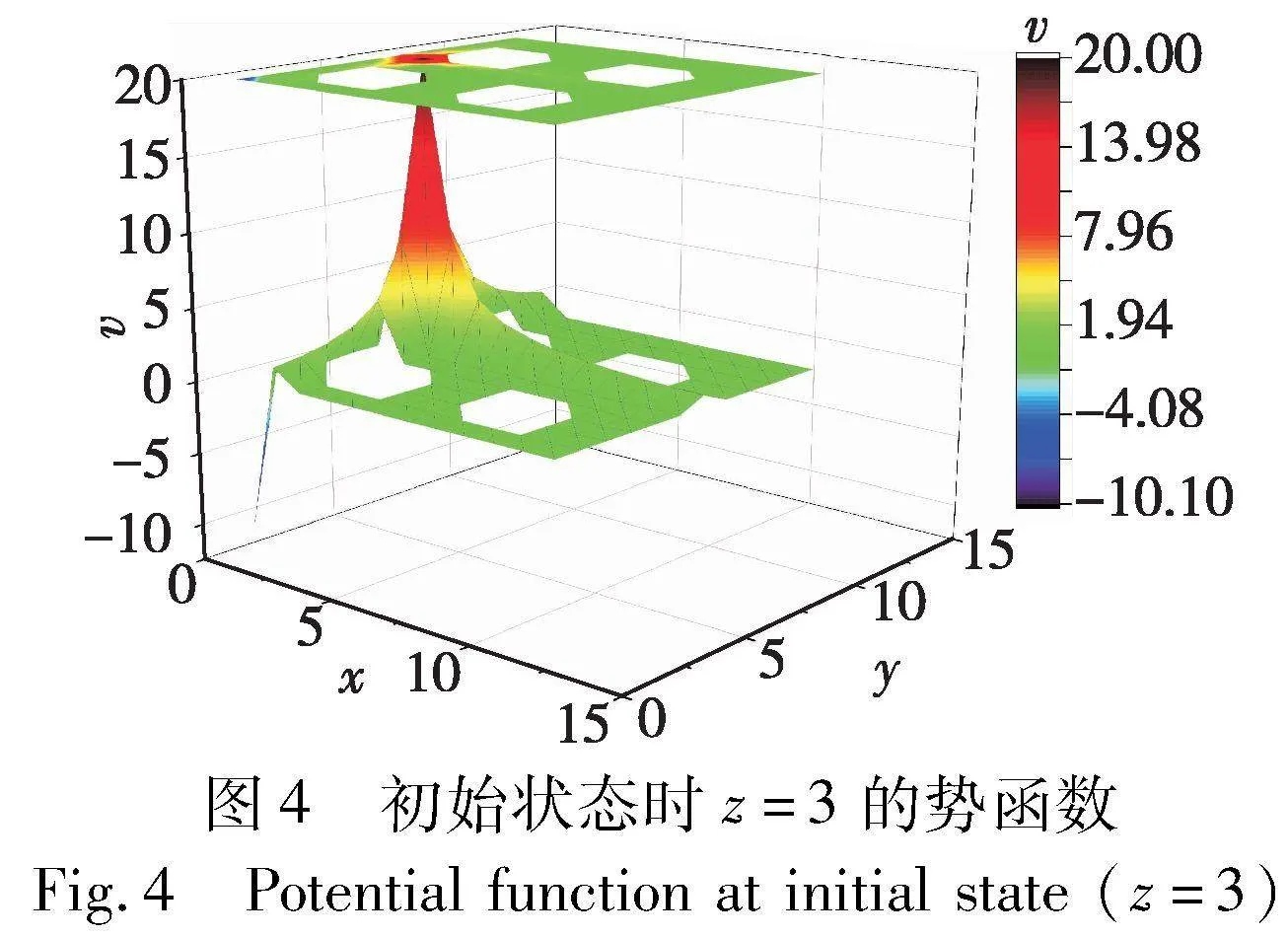
其中:μ(·)是权重系数函数;jpositive是积极权重系数;jnegative是消极权重系数,权重系数取值(0,1);vχ是式(2)状态中的预测奖励;χ是该项的方向;dχ是式(2)状态中的距离;X是方向集合。给出初始环境一个平面的势函数图,如图4所示。
图4中平面坐标与动态迷宫环境一致,V轴表示势函数的值。空白区域代表该处不可达。
其中:mboring是Boring函数的系数;loopBody(·)用于求取Str倒序中以最新状态开始的无聊子序列的长度,无聊子序列在Str倒序中需连续重复出现;circleNum(·)用于求取无聊子序列在Str倒序中连续重复出现的次数,可以根据事件集B中的事件触发次数获取。
2.4 动态三维迷宫的综合奖励算法
动态三维迷宫综合奖励的单步流程如算法1所示。综合奖励算法是强化学习中的奖励函数部分,整体的奖励过程由相同的综合奖励单步流程构成。单步奖励流程中首先通过事件触发机制得到本步的触发事件集合,触发事件直接影响环境奖励。接着进行内部奖励的计算,最后根据环境奖励和内部奖励得出本步的综合奖励。
算法1 Single-step for integrated reward
3 实验结果与分析
3.1 实验环境
对迷宫环境建立笛卡尔坐标系,以坐标轴的正负指向定义方向X。agent与animal活动空间位于第Ⅰ象限。以实体距离原点最近的顶点坐标代表实体坐标,实体向某方向紧邻单元移动简化为单个坐标的平移,移动过程以一个立方体为单位。
animal移动策略: animal分为3组,第1组两个animal从初始位置开始随机行动;第2组animal分别关联两个target,当自身位置距离关联target太近则远离target,太远则靠近target,在合适的空间范围则随机移动;第3组2个animal则分别顺时针和逆时针在边长不同、高度相同的框面中以反复螺旋方式移动。
3.2 对比方案和实验设置
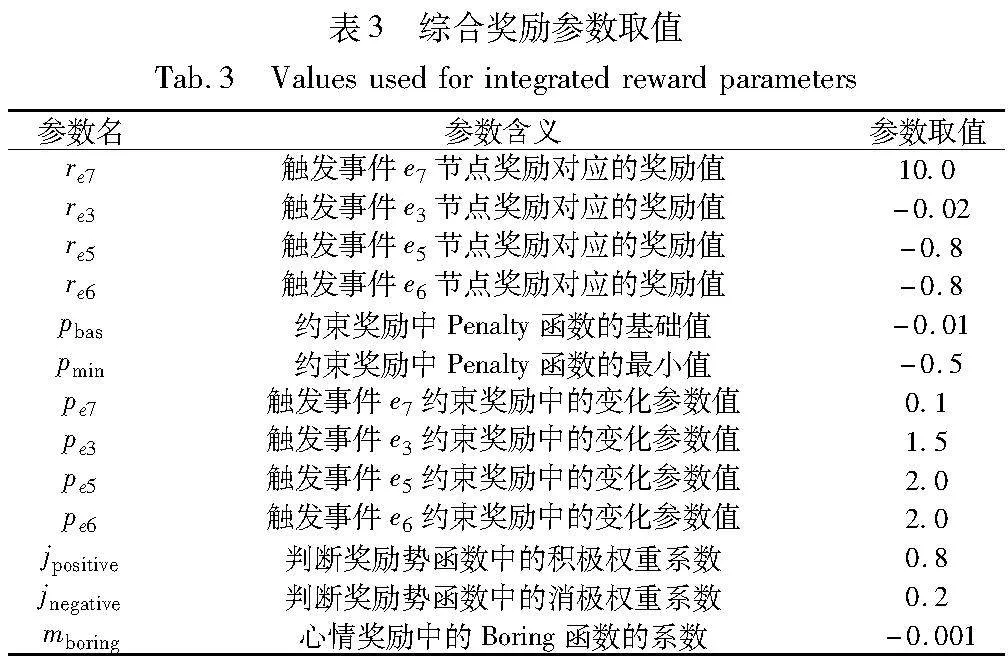
奖励设计方案包括简单奖励、改进奖励和综合奖励。综合奖励参数取值如表3所示。奖励方案设置的区别如表4所示。
评价指标:实验以式(4)成就值作为主要评价指标,并分析评估三种奖励方案中,agent轨迹和状态数目方面的表现。
强化学习算法:算法采用Q-learning,动作行为策略为常规的ε-greedy方法。探索因子ε=0.1,学习因子α=0.1,折扣因子γ=0.9。
3.3 动态三维迷宫环境下的实验结果
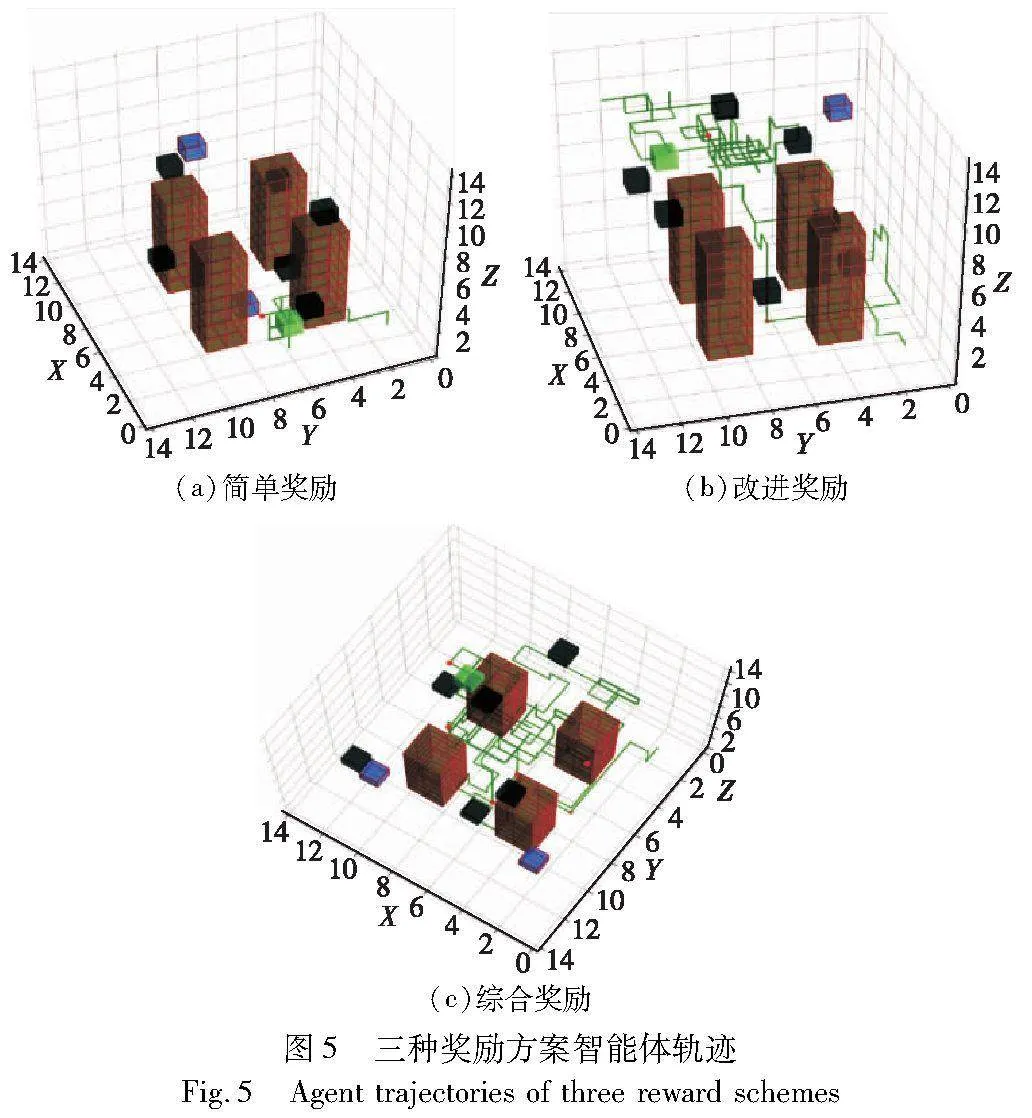
考虑奖励方案的长期及训练中的性能表现,每万轮记录奖励方案的Q表。agent轨迹可以直观反映三种奖励方案在动态三维迷宫任务中的表现。使用300万轮三种奖励方案各自的Q表,单轮agent运动轨迹如图5所示。
图5(a)表明,采用简单奖励方案的agent倾向于保守行动,出现大量重复和原地不动行为,躲避行为较少,整体轨迹单调,绿色轨迹上的1个红点表明该轮训练中只到达target坐标一次。图5(b)表明,改进奖励中,轨迹显示agent探索到初始状态的另一target区域,改进方案的智能体轨迹相较于简单奖励更为复杂,躲避animal的行为更明显,很少出现原地不动的行为,但仍有明显的重复行为,图中绿色轨迹上的2个红点代表改进奖励方案的agent在此轮中到达target位置两次(参见电子版)。图5(c)采用综合奖励的agent表现出明显的活跃性,很少出现重复或原地不动的行为,图中大多数轨迹显示出agent的目的性,即躲避animal或向target移动,轨迹上的复数红点表明agent途径范围囊括了更多的target。
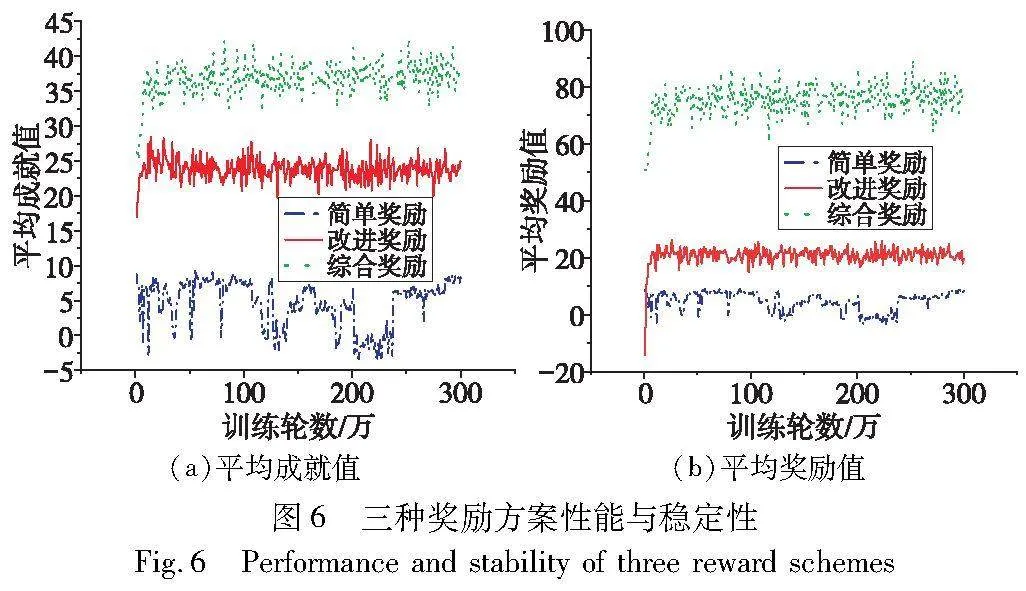
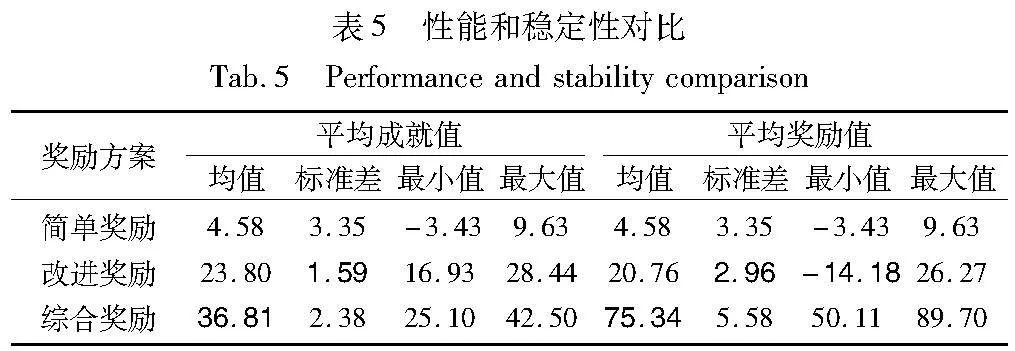
使用记录的Q表,三种方案每种300共计900个Q表,对方案的成就值和奖励值进行比较,均值由各Q表独立训练100次求得,结果如图6、表5所示。图6 (a)是三种奖励条件下不同训练轮数时的成就值,简单奖励方案中成就值较低,为-3.43~9.63,标准差3.35较大,表明简单奖励性能较差且不稳定;改进奖励中分布比较密集,标准差1.59,表明其性能较为稳定;综合奖励的成就值在25.10~42.50,均值相较于改进奖励提升54.66%。数据表明,综合奖励方案实现目标的性能优于改进奖励和简单奖励。图6 (b) 显示三种奖励方案对平均奖励的影响。在平均奖励稳定性方面,综合奖励方案不及改进奖励,不过不影响综合奖励在实现目标方面的性能。
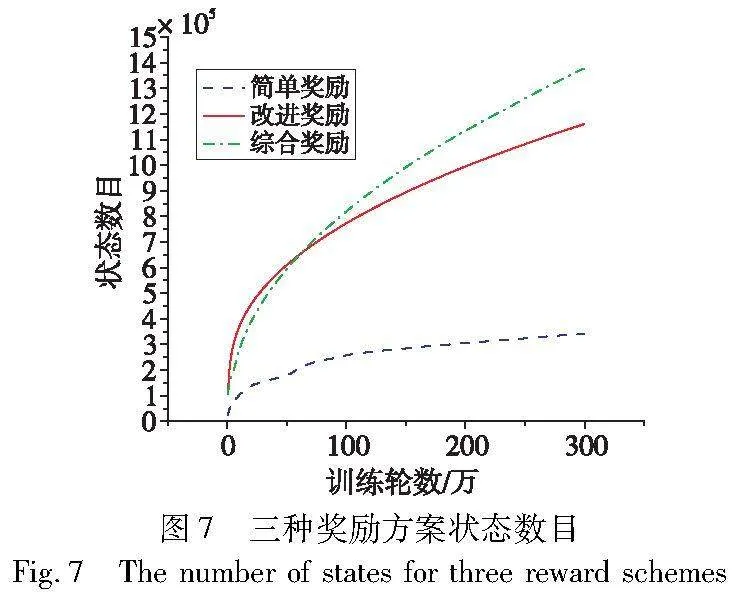
图7展示了300万轮训练中三种奖励方案的状态数目变化。可以发现,简单奖励整体较为平缓,综合奖励多于改进奖励,增长趋势都逐渐下降。三种方案的最终状态数目分别是34.3万、116.1万、137.9万。综合奖励状态数目约是改进奖励的1.188倍,约是简单奖励的4倍。状态数目与智能体的探索能力相关,在策略相同的条件下,综合奖励的探索能力优于改进奖励和简单奖励。
最终,通过计算三种方案的平均成就值、平均奖励值、最终状态数目说明三种方案的比较结果,其中平均成就值体现完成任务的能力,平均奖励的大小体现奖励函数的塑形能力,最终状态数目说明探索能力的强弱。以上数据与分析说明,综合奖励在完成任务、探索能力方面优于传统奖励方案和改进奖励方案。
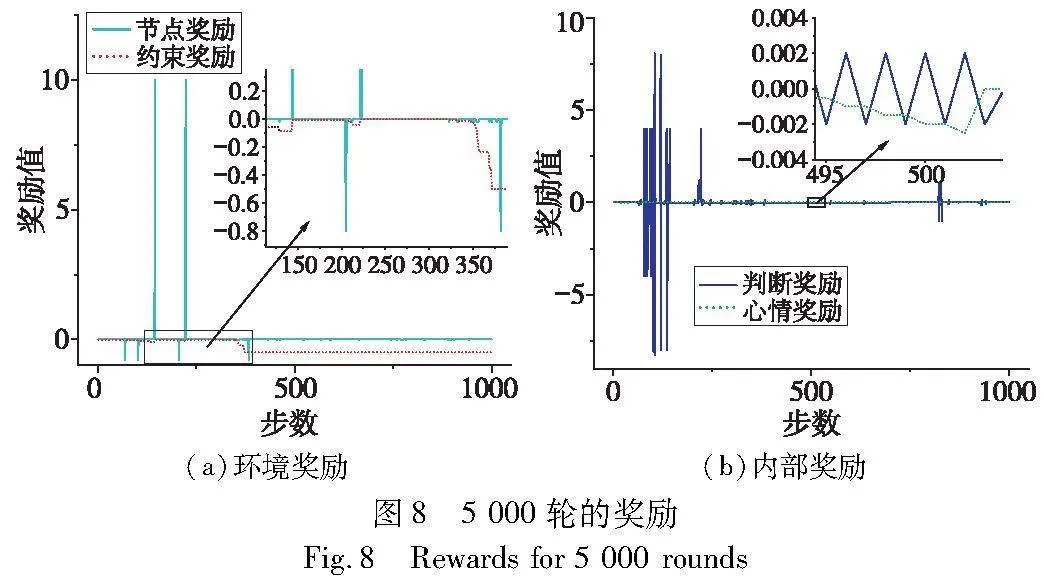
进一步分析综合奖励的组成,抽取第5 000轮时环境奖励与内部奖励一轮中的变化图,如图8所示。图8(a)环境奖励中,节点奖励非零值对应奖励集G中的节点事件,并使约束奖励发生变化,节点奖励中高峰值10对应e7,负值对应其他节点事件。约束奖励后半段到达最小值,则不再因负面节点事件减小。图8 (b)内部奖励中判断奖励的正负对冲状况十分明显,表明此时agent出现重复行为,但在节点奖励高峰对应的140步和222步前,判断奖励为4左右的正奖励无对应负奖励,表明判断奖励辅助agent到达target位置。心情奖励的频繁波动与判断奖励代表的agent重复行为相对应,触发e1事件时,心情奖励以鼓励新行为的方式影响决策。
同时从图8看出,节点奖励与约束奖励直接源于任务要求,奖励值成分重,是完成任务的主要参考。判断奖励数量级较大,但因势函数特性不会干扰任务目标。心情奖励数量级远低于节点奖励,不会影响任务主体方向,当出现对应的不利任务行为时,心情奖励能辅助算法作出更符合期望行为的决策,因此综合奖励相对于改进奖励改善了agent的重复低效行为。
改变迷宫环境,主体障碍高度改为3,新增两处障碍,改变动态障碍物规则,将目标物的数量增加至4,使用综合奖励方案运行一次,得到图9。智能体探索行为增多,轨迹上4个红点表示多次到达target位置。使用原环境学习后的综合奖励设计的Q表,在改变后的迷宫环境中仍表现出较高的性能,表明综合奖励设计与具体环境没有深耦合,在同类任务迁移中具有可行的泛化能力。
4 结束语
动态三维迷宫具有动态随机的特性,对强化学习具有挑战性,本文提出一种基于事件触发的综合考虑奖励设计思路,用于提高动态三维迷宫的强化学习效果。理论分析与实验表明,简单奖励采用传统奖励函数中的稀疏奖励方案,无法适应任务环境的动态特性,表现不佳且稳定性差;改进奖励中增加的约束奖励相关函数改善了简单奖励的保守策略,但对于更好地完成任务缺乏方向性;综合奖励方案以事件触发为基础,综合了奖励塑造和内在动机,提出环境和内部的内外奖励思路,在性能和探索能力方面表现更好。三维迷宫中的综合奖励函数设计思想可应用于大型复杂的强化学习场景,例如利用机械臂在动态空间中抓取可移动的目标物,探索困难任务的学习训练过程。
参考文献:
[1]Dewey D. Reinforcement learning and the reward engineering principle [C]// Proc of AAAI Spring Symposium on Series. 2014.
[2]逄金辉,冯子聪. 基于不确定性的深度强化学习探索方法综述 [J]. 计算机应用研究,2023,40(11): 3201-3210. (Pang Jinhui,Feng Zicong. Exploration approaches in deep reinforcement learning based on uncertainty: a review [J]. Application Research of Computers,2023,40(11): 3201-3210.)
[3]Ng A Y,Harada D,Russell S. Policy invariance under reward transformations: theory and application to reward shaping [C]// Proc of the 16th International Conference on Machine Learning. San Francisco,CA: Morgan Kaufmann Publishers Inc.,1999: 278-287.
[4]Riedmiller M,Hafner R,Lampe T,et al. Learning by playing solving sparse reward tasks from scratch [C]// Proc of International Confe-rence on Machine Learning. [S.l.]:PMLR,2018: 4344-4353.
[5]Wiewiora E,Cottrell G W,Elkan C. Principled methods for advising reinforcement learning agents [C]// Proc of the 20th International Confe-rence on Machine Learning. Palo Alto,CA: AAAI Press,2003: 792-799.
[6]Cai Mingyu,Xiao Shaoping,Li Junchao,et al. Safe reinforcement learning under temporal logic with reward design and quantum action selection [J]. Scientific Reports,2023,13(1): 1925.
[7]Singh S,Lewis R L,Barto A G. Where do rewards come from?[C]// Proc of Annual Conference of the Cognitive Science Society. 2009: 2601-2606.
[8]Singh S,Lewis R L,Barto A G,et al. Intrinsically motivated reinforcement learning: an evolutionary perspective [J]. IEEE Trans on Autonomous Mental Development,2010,2(2): 70-82.
[9]Ren Jinsheng,Guo Shangqi,Chen Feng. Orientation-preserving rewards’ balancing in reinforcement learning [J]. IEEE Trans on Neural Networks and Learning Systems,2021,33(11): 6458-6472.
[10]Van Seijen H,Fatemi M,Romoff J,et al. Hybrid reward architecture for reinforcement learning [EB/OL]. (2017-11-28). https://arxiv.org/abs/1706.04208.
[11]Icarte R T,Klassen T,Valenzano R,et al. Using reward machines for high-level task specification and decomposition in reinforcement lear-ning [C]// Proc of International Conference on Machine Learning. [S.l.]:PMLR,2018: 2107-2116.
[12]Camacho A,Icarte R T,Klassen T Q,et al. LTL and beyond: formal languages for reward function specification in reinforcement learning [C]// Proc of the 28th International Joint Conference on Artificial Intelligence. 2019: 6065-6073.
[13]Li Mike,Nguyen Q D. Contextual bandit learning with reward oracles and sampling guidance in multi-agent environments [J]. IEEE Access,2021,9: 96641-96657.
[14]Icarte R T,Klassen T Q,Valenzano R,et al. Reward machines: exploiting reward function structure in reinforcement learning [J]. Journal of Artificial Intelligence Research,2022,73: 173-208.
[15]Furelos-Blanco D,Law M,Jonsson A,et al. Hierarchies of reward machines [C]//Proc of International Conference on Machine Learning. [S.l.]:PMLR,2023: 10494-10541.
[16]Huang Changxin,Wang Guangrun,Zhou Zhibo,et al. Reward-adaptive reinforcement learning: dynamic policy gradient optimization for bipedal locomotion [J]. IEEE Trans on Pattern Analysis and Machine Intelligence,2023,45(6): 7686-7695.
[17]Tang Bixia,Huang Y C,Xue Yun,et al. Heuristic reward design for deep reinforcement learning-based routing,modulation and spectrum assignment of elastic optical networks [J]. IEEE Communications Letters,2022,26(11): 2675-2679.
[18]Kvári B,Pelenczei B,Aradi S,et al. Reward design for intelligent intersection control to reduce emission [J]. IEEE Access,2022,10: 39691-39699.
[19]Goh H H,Huang Y,Lim C S,et al. An assessment of multistage reward function design for deep reinforcement learning-based microgrid energy management [J]. IEEE Trans on Smart Grid,2022,13(6): 4300-4311.
[20]Zhang Hao,Lu Guoming,Qin Ke,et al. AInvR: adaptive learning rewards for knowledge graph reasoning using agent trajectories [J]. Tsinghua Science and Technology,2023,28(6): 1101-1114.

