基于改进粒子群算法的机械臂能耗轨迹优化
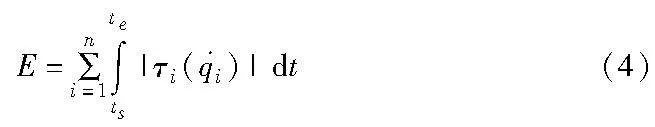
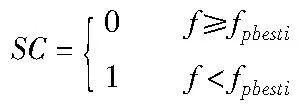
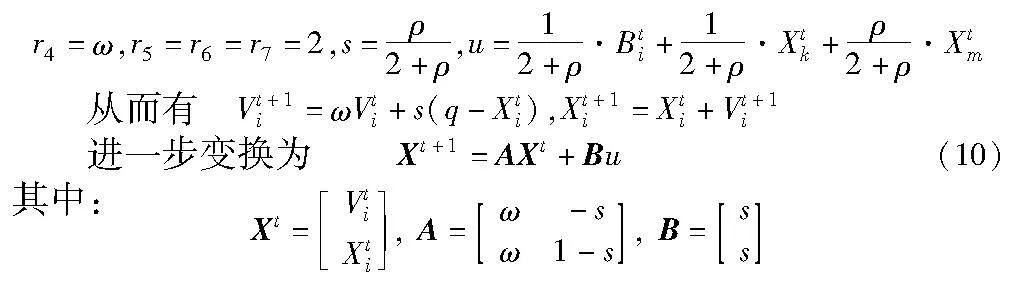





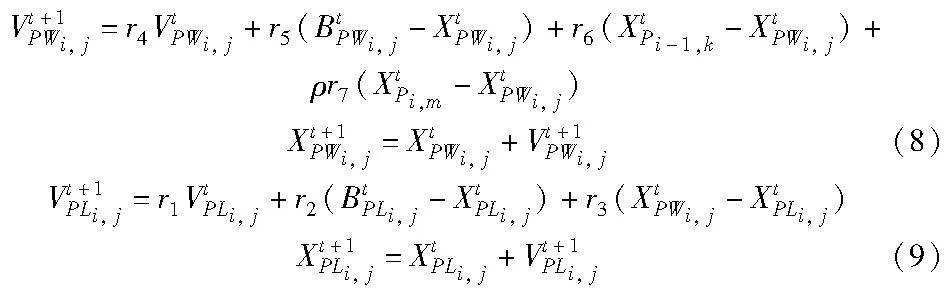


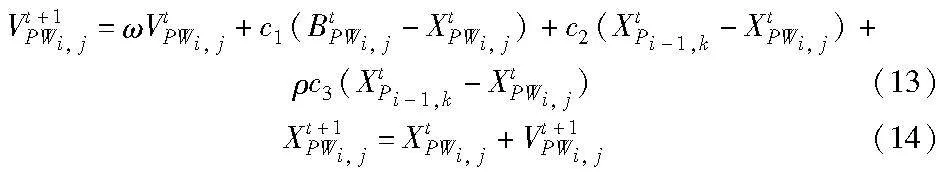

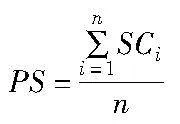
摘 要:针对工业机器人能耗轨迹优化问题,提出了一种基于金字塔层拓扑结构的粒子群算法。该算法引入了金字塔层式的拓扑结构,将粒子进行排序、分层,从而改进算法的竞争策略,增加了种群多样性;引入了新的合作策略以更新粒子的速度和位置;引入胜利百分比来自适应地调整粒子群算法的权重系数,提高了粒子的搜索效率。为了验证该算法的有效性,在测试函数集上进行了测试,并与其他八种变体粒子群算法进行比较,结果表明所提出的算法性能具有显著优势。最后将该算法应用到工业机器人轨迹规划中,仿真实验表明该算法能有效求解机器人的能耗最优轨迹,机器人的能耗明显减低,且满足工业机器人的运动学及动力学约束。
关键词:机械臂;最小能耗;轨迹规划;拓扑结构;改进粒子群算法
中图分类号:TP242 文献标志码:A文章编号:1001-3695(2024)06-007-1649-07
doi: 10.19734/j.issn.1001-3695.2023.10.0441
Optimisation of energy consumption trajectory of robotic arm based on improved particle swarm algorithm
Abstract:This paper proposed a particle swarm algorithm based on pyramid layer topology to optimize energy consumption trajectories of industrial robots. The algorithm introduced a pyramid layer topology to sort and stratify the particles thus improving the competitive strategy of the algorithm and increasing the population diversity. The algorithm introduced a new cooperation strategy to update the speed and position of the particles. It introduced a victory percentage to adaptively adjust the weight coefficients of the particle swarm algorithm and improved the search efficiency of the particles. In order to verify the effectiveness of the algorithm, this paper tested it on the set of test functions and compared it with other eight variants of particle swarm algorithms. The results show that the performance of the proposed algorithm has significant advantages. Finally, it applied the algorithm to industrial robot trajectory planning. Simulation experiments show that the algorithm can effectively solve the optimal trajectory of the robot’s energy consumption, and the energy consumption of the robot is significantly reduced, which meets the kinematics and dynamics constraints of industrial robots.
Key words:robotic arm; minimum energy consumption; trajectory planning; topology; improved particle swarm algorithm
0 引言
工业机器人的节能降耗是绿色智能制造系统发展中的焦点问题之一[1]。由于多关节机器人的轨迹优化具有高自由度性、强非线性及高度耦合性,导致难以用解析法直接求解,安凯等人[2]通过降低自由度并基于变分法求解了平面机械臂的能耗最小路径,但解析法难以解决空间高维机器人的轨迹规划问题,所以有很大的局限性。因此,有大量学者将轨迹优化转换为大规模非线性规划问题,从而应用智能算法来求解工业机器人的最小能耗轨迹。贺莹等人[3]针对码垛机器人的“门字形”路径,提出遗传算法以求解最优能耗轨迹;贾文友等人[4]提出改进蜻蜓算法用以点焊机器人的轨迹优化;邓乾旺等人[5]则采用蜜蜂进化型遗传算法求解点焊机器人的最优能耗轨迹;Chai等人[6]使用偏置粒子群优化方法来处理机器人约束轨迹设计问题;Lu 等人[7]利用增量拉格朗日约束粒子群优化算法来解决机器人的时空最优轨迹规划问题;Deng等人[8]引入了一种新颖的差分进化算法来建立码垛机器人的能耗模型,从而优化轨迹;Saravanan等人[9]基于惰性非支配排序遗传算法和微分进化的进化算法,用于考虑有效载荷约束的工业机器人机械手的最优轨迹规划。以上算法对机器人的节能降耗都具有一定的作用,但存在着陷入局部最优和过早收敛等问题,所以提升优化算法的性能是能耗轨迹优化的主要问题之一。
在智能优化算法中,粒子群优化算法(PSO)具有简单、有效和计算成本低的优点,但标准PSO也存在着局限性,为了提升PSO的性能,研究人员从参数调整、学习策略、与其他进化算法的结合等方面对PSO进行了改进,这些PSO变体相比标准PSO,提高了搜索能力。Li等人[10]通过提出多信息融合的三变量迭代惯性权重系数来改进粒子群算法;谢美华等人[11]则结合Q学习来设计参数的自适应调整策略,从而改进PSO;Ye 等人[12]提出了一种动态多群粒子群优化方法学习策略以提高PSO的性能;Zhang等人[13]将差分变异和具有社会学习的行为结合来改进粒子群算法;Laskar等人[14]将鲸鱼算法引入粒子群算法中,以提升PSO的性能;Karimi-Mamaghan等人[15]通过集成机器学习来改进PSO。这些改进策略对标准PSO的性能都具有一定的提升作用,但都无法完全避免其算法陷入局部最优和过早收敛。为了进一步提升PSO算法的性能,本文基于金字塔式的拓扑结构和胜利百分比,提出一种改进的粒子群算法,并用于求解机器人的能耗最优轨迹,计算结果表明,融合新拓扑结构的自适应粒子群算法的稳定性、收敛速度和收敛性能都明显提高。对机械臂进行仿真实验,其结果表明,得到的最优轨迹能满足约束条件,证明了所改进的粒子群算法的可行性。
1 基于五次多项式的轨迹规划
本文在机械臂的关节空间中,针对机械臂所必经的n个关键点,两点之间用五次多项式连接,五次多项式在进行机械臂的点到点轨迹优化时,不仅满足速度、加速度连续,还可以保证加加速度的连续,可使机械臂减少振荡,运行更加平稳[16],所以本文在关节空间中基于五次多项式规划两点间的轨迹,其轨迹函数表达式为
q=a0+a1t+a2t2+a3t3+a4t4+a5t5(1)
其中:q 为关节角位置;a0、a1、a2、a3、a4、a5 为轨迹方程代求的系数。考虑到在此段轨迹中起始点和终止点的约束,得到以下方程:
qs=a0+a1ts+a2t2s+a3t3s+a4t4s+a5t5svs=a1+2a2ts+3a3t2s+4a4t3s+5a5t4sαe=2a2+6a3te+12a4t2e+20a5t3eqe=a0+a1te+a2t2e+a3t3e+a4t4e+a5t5eve=a1+2a2te+3a3t2e+4a4t3e+5a5t4eαe=2a2+6a3te+12a4t2e+20a5t3e
整理上式得到
其中:ts、te分别为起始点和终止点的时间; qs、vs、αs、qe、ve、αe 分别为起始点的角位置、角速度、角加速度和终止点的角位置、角速度及角加速度。
通过式(2)可求解出轨迹函数的代求系数,从而完成轨迹规划。对于多段的轨迹规划,由于要求各段轨迹在连接点时仍能保证轨迹的连续,所以只要将上一段轨迹终止点的约束条件作为此段轨迹起始点的约束条件,代入式(2),就能确定多段整体的轨迹函数,且满足各关键点的速度、加速度连续。
2 能耗模型的建立
牛顿-欧拉递推法、拉格朗日分析法是建立机械臂动力学方程的主要方法,牛顿-欧拉法是基于牛顿-欧拉公式,通过递推的方式计算连杆的速度和加速度,从而得到整个机械臂的动力学方程。拉格朗日方程则是基于能量的动力学方法。已经证明这两种方法得到的动力学方程是等价的,但拉格朗日方程形式简洁,得到串联机械臂的方程可以写为[17]
只考虑关节驱动力矩所作的功,则整个机械臂的能耗为[18]
其中:i=1,2,…,n 为机械臂的关节数目;τ(i)是关节力矩矢量τ 的第i 个分量。
虽然建立了能耗模型,但只有转换成优化问题,才能利用各类的智能算法进行求解。形成能耗优化问题可以通过建立能耗与某一物理量的函数,也可以通过优化与参考轨迹的偏差来间接得到[11]。本文通过建立各段规划轨迹的时间和能耗的函数关系来形成优化问题。容易知道机械臂的运动学及动力学约束条件为
3 粒子群优化算法
3.1 标准粒子群优化算法
粒子群优化算法[19]是一种典型的群智能优化算法,最初由Eberhart和Kennedy于1995年提出,用于模拟鸟类觅食行为。PSO由N个粒子组成,粒子的运动就是粒子群在d维搜索空间D中搜索最优解的迭代过程。每个粒子在任何时候都有自己的速度和位置,而位置则表示特定问题的解。对于第t次迭代的第i个粒子,其速度和位置为
vid(t+1)=ωvid+c1r1×(pid-xid(t))+c2r2×(pgd-xid(t))
xid(t+1)=xid(t)+vid(t) 1≤i≤n,1≤d≤N(7)
其中:vid(t)为第t次迭代后粒子速度向量的第d维分量;xid(t)为第t次迭代后粒子位置向量的第d维分量;pid为粒子历史最优解pbest对应位置的第d维分量;pgd为群体最优解pgest对应位置的第d维分量;c1、c2为学习因子;r1、r2为[0,1]的随机数。
3.2 改进金字塔层拓扑结构的粒子群算法
标准PSO由于其拓扑结构简单,导致其粒子间的竞争与合作策略形式单一,容易使算法早熟和收敛到局部解。已有相关研究通过改变标准PSO的拓扑结构来提升算法的性能,典型的邻域结构包括星形、环形、球形、金字塔形及冯·诺伊曼结构等,根据问题特性,配置适当的邻域结构,有利于实现 PSO 算法的自适应搜索。Wu等人 [20]提出了一种基于欧几里德距离的自适应拓扑结构,增大了粒子群的多样性,从而提高了PSO的整体性能;Zhang等人[21]将一种基于集群的具有领导者更新机制的环形拓扑应用于PSO,并求解了多目标优化问题(MMPO),其结果表明,环形拓扑结构能够保持种群的多样性,提高PSO的性能;Yao等人[22]提出将单向动态混合力拓扑结构应用于 PSO算法。本文通过构造金字塔层式的拓扑结构[23]来改进PSO算法的竞争及学习策略,从而提升PSO的性能。
3.2.1 构建金字塔层
算法1 构建金字塔层(PB)
在算法1的第6行中,PPi, j 表示金字塔第i层的第j个粒子。因此金字塔层结构具有以下特性:a)每个粒子被分配到特定的层;b)粒子所在的层越高,粒子则越优,全局最佳粒子位于顶层,而最差的粒子位于底层;c)同一层的粒子具有相近的适应度值。
3.2.2 竞争策略
与标准PSO相比,除了与历史最优竞争外,PPSO采取了另外两种竞争策略。首先,在构建金字塔时,所有粒子都参与排序,以决定它们在金字塔中的层。由于分选涉及所有粒子,称之为全局竞争策略。其次,将每个粒子都置于特定的层中,对不同层的粒子进行不同的处理,从而提高其有效性。基于此,除顶层外的其他层粒子随机配对,根据适应度值分为胜者组和败者组两组。胜者可以从更高层的粒子中学习,而败者只能从同一层的获胜者中学习。由于竞争只涉及同层的粒子,可以称为局部竞争策略,描述如算法2所示。
算法2 金字塔层中的竞争
本文所提出的竞争策略使全局最优的粒子位于顶层,所有的粒子可以从比自己更优的不同的粒子中学习,而不是像标准PSO那样从唯一的全局最优粒子学习。因此,竞争策略提高了粒子种群的多样性。
3.2.3 合作策略
理想的合作策略是每个粒子都有机会与更多的粒子合作,不仅是与全局最优的粒子,而且是任何其他比当前粒子更优的粒子。这样,合作的多样性将得到增强,从而能获得更好的性能。基于此提出了一种新的合作策略,即每个粒子都有机会与除了最优粒子之外的几个更优的粒子合作。首先,同一层的败者与它们的历史最优值及同层的胜者合作。其次,除了那些在顶层的粒子,其他的胜者将与包括其他上层的粒子及顶层的粒子合作。基于此,第i层(i=2,3,…,L)粒子的胜者和败者分别根据式(3)(4)更新它们的速度和位置。
其中:ri 为(0,1)的随机数;ρ 为用来控制顶层粒子对当前粒子影响的常数;PLij、PWij 分别表示第j个粒子在第i层的败者和胜者; Xtp、Vtp、Btp 分别表示粒子p在t次迭代的位置、速度和历史最佳值;k和m分别是不大于ni-1和ni的随机正整数。
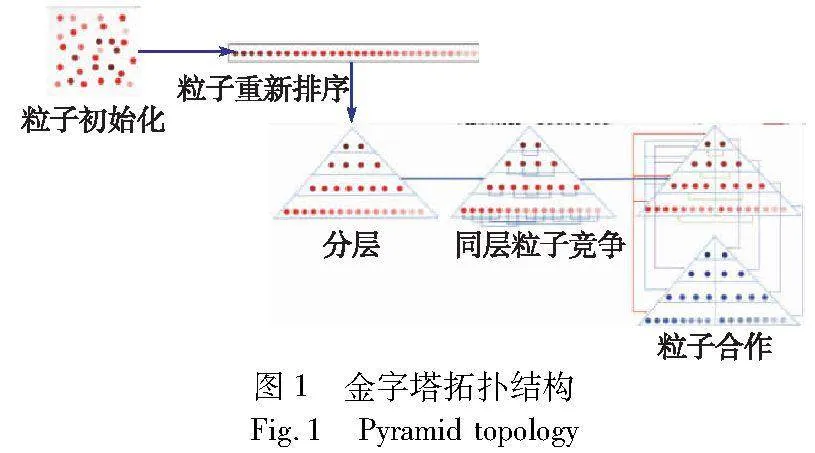
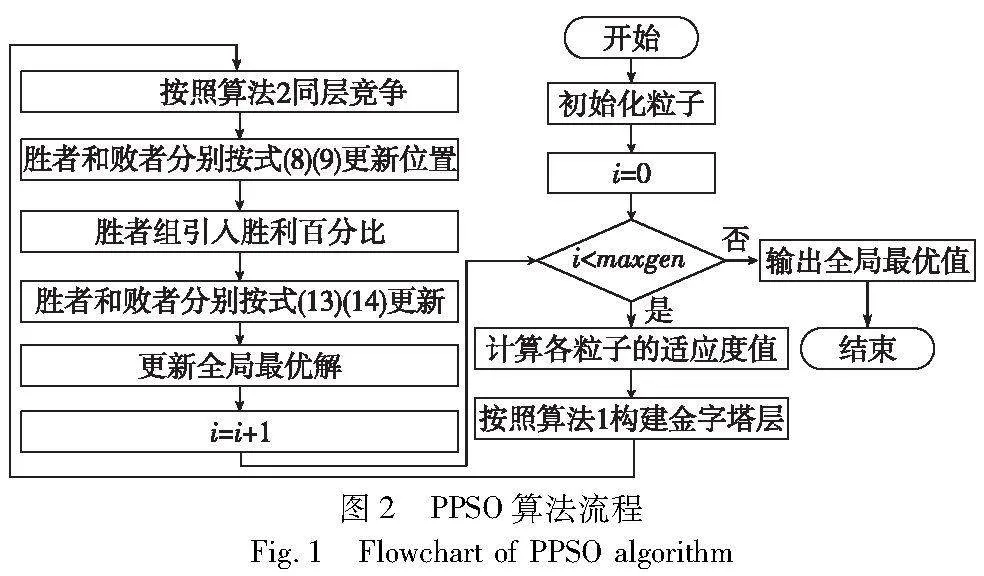
PPSO的框架如图1所示,在每一代中,粒子根据它们的适应度以升序排序。在图1中,粒子越优,其颜色越深。接下来,每个粒子被分配到金字塔中的特定层,从上到下,从左到右,通过其在排序粒子中的索引。因此粒子越优,它在金字塔中的层就越高。然后,每一层的粒子将随机配对,产生胜者和败者。胜者和相应的败者分别放置在图1的左侧和右侧。最后,每一层的败者将从同一层的相应胜者以及自身的历史最优中学习。相比之下,除了第1层的胜者之外,胜者将有机会从更优的粒子中学习,即向更高层的粒子、粒子群中最优的粒子(第1层的粒子),以及获胜者的历史最佳者学习。第1层的胜者将直接转移到下一代。在图1中,蓝色粒子表示红色粒子在相应位置的历史最优值(参见电子版)。
3.2.4 收敛性分析
在PPSO中,胜者和败者有不同的更新策略,由于失败者的动态分析与成功者的动态分析相似,但比胜者的更容易,所以本文主要分析胜者组的动态行为。对于式(8),令
根据李雅普诺夫平衡点理论[24],只要矩阵A的特征值λ1 、λ2 满足|λ1|≤1,|λ2|≤1,就能说明系统的平衡点是稳定的,也就说明粒子最终是收敛的。矩阵A的特征值为式(11)的解,从而有
|A-λE|=0(11)
即得λ2+(s-1-ω)λ+ω=0,由韦达定理推出0<ω<1,s>0。因此,ρ>-2 是种群中胜者收敛的充分条件。该分析可以引入到PPSO中的败者组。保证ρ ≥ 0及0<ω<1成立,就能满足粒子收敛。需要指出的是,粒子群优化算法虽然满足粒子收敛的条件,但并不能保证收敛到全局最优。
3.2.5 胜利百分比
通过引入粒子朝向最优值的成功率来进一步改进惯性权重系数。首先提出胜利百分比(PS)[25]的概念。胜利百分比越高,收敛到远离局部最佳点的程度就越高,因此该组粒子以更慢的方式向全局最佳解前进。同样,较低的胜利百分比意味着所有粒子都倾向于在局部最佳点周围振荡而没有任何进一步的增强。通过使用粒子的胜者个数(SC)来确定胜利百分比。本文为求解最小值问题,所以,如果当前迭代中的适应度与在较早迭代中获得的值相比更小,则SC被设置为1。在t次迭代时的粒子i,其SC可由下式计算:
PS根据SC计算:
其中:n是粒子的数量,并且PS位于0~1,其指示在先前迭代中具有其适应度的改善粒子的百分比。基于更新胜利百分比的自适应惯性权重为
ω=(ωmax-ωmin)PS+ωmin(12)
从而胜者组的速度、位置按式(13)(14)更新,而败者组不改变更新方式。
3.2.6 复杂度分析
由于适应度评估的时间取决于实际问题,可以假定适应度的复杂度是相同的,将重点放在最后三个部分。在构建金字塔时,PPSO首先需要对整个群体中的粒子进行排序,然后将每个粒子分配到特定的层,如算法1所示。对于第一个操作,任何排序算法,如快速排序、选择排序、归并排序等,对于群中的N个粒子,排序的平均时间复杂度为O(N log2(N))。第二种操作只需要扫描整个群体一次,然后将每个粒子分配到L层中的一层,其复杂度为O(N)。因此,金字塔构建的总时间复杂度为O(N log2(N)+N)。配对操作只需扫描整个种群一次,因此其时间复杂度为O(N) 。假设每个粒子的维度都是D,除了第一层的胜者将直接进入下一代,N个粒子将在合作中更新D维度。因此,学习时间复杂度为O(ND)。由此得到PPSO的时间复杂度为O(N log2(N)+N+DN),略高于标准PSO的O(ND)。
该粒子群优化算法有四个主要概念,分别是构建金字塔层、将同层粒子分为胜者和败者的竞争策略、胜者和败者使用不同规则更新合作策略以及在胜者组中引入胜利百分比。本文PPSO算法流程如图2所示。
3.2.7 PPSO算法性能分析
为了说明PPSO算法的收敛精度,在12个测试函数集[26]上进行测试,并和标准PSO及8种最先进的PSO变体,包括WPSO[27]、MPSO[28]、UPSO[29]、 DENPSO[30]、 HAPSO[31]、DMPSO[32]、GAPSO[33]及CPSO在测试函数集上进行比较分析。
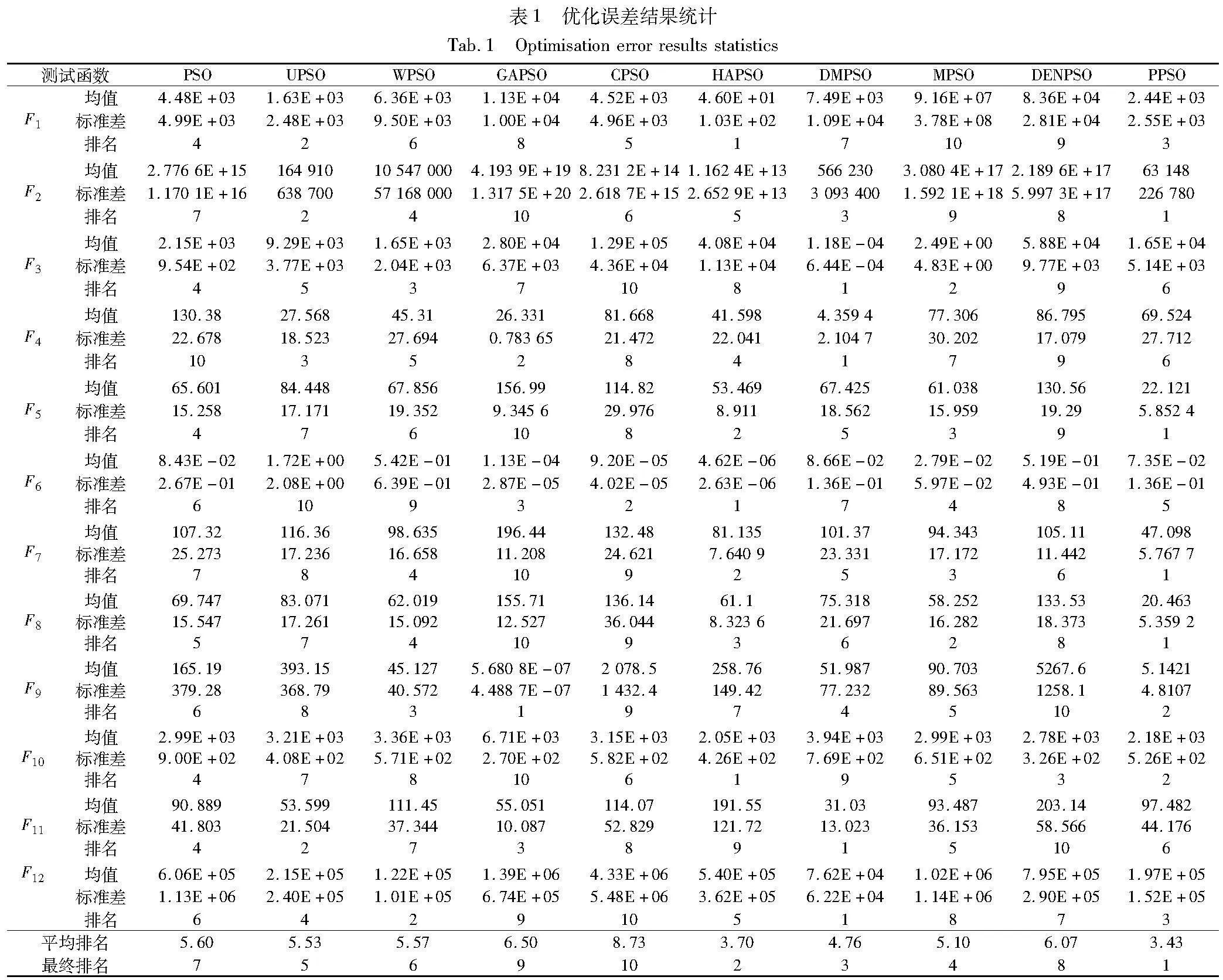
所有的计算都是在相同维度下进行的,即d=30,并将所有算法的种群规模和最大适应度值分别设置为64和10000d。对于PPSO,使用4-8-20-32的金字塔结构进行比较,并且ρ设为0.02。每个算法在每个测试函数上进行30次运算,基于误差的平均值、标准差和排名来评价收敛精度,均值反映了算法的优化能力,而标准差反映了算法的稳定性,运行结果如表1所示。可以看到,PPSO的平均排名为3.43,综合排名为1,相比其他8种变体PSO,其在测试函数上的收敛精度表现最优。虽然UPSO和标准PSO也达到最佳均值,但它们最终的性能不如PPSO。
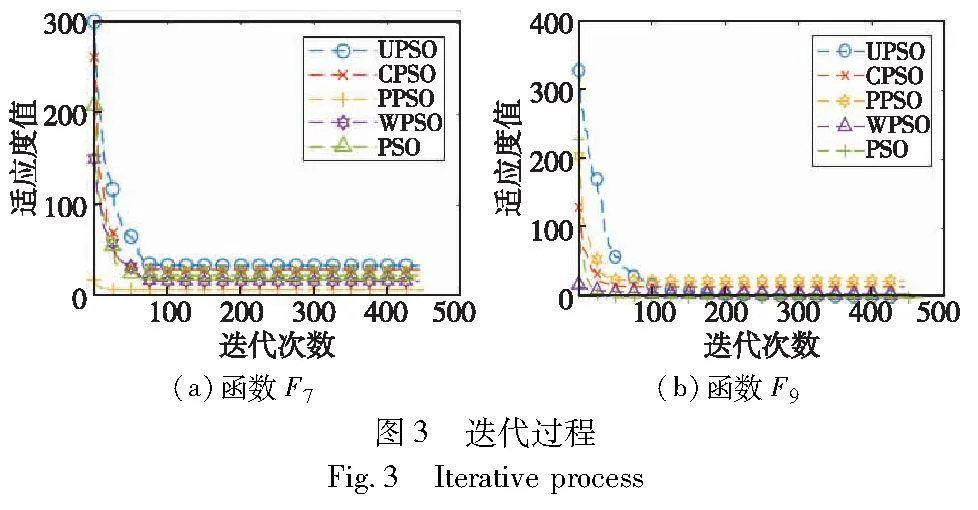
为了评价PPSO的效率,在表2中列举了PPSO及变体PSO算法在测试函数集上的运行时间。可以看出,标准PSO在12种测试函数上都达到了最少的运行时间,明显优于其他变体粒子群算法,其原因是PSO的竞争合作机制单一,导致其复杂度低。PPSO运行时间的平均排名为5.50,综合排名为5,其运行效率较标准PSO略差。选取测试函数F7及F9,得到PPSO及变体PSO的迭代过程,如图3所示。
可以看出,在F7及F9的测试函数上PPSO的迭代性能都明显优于其他算法。
4 仿真实验
4.1 仿真环境设置
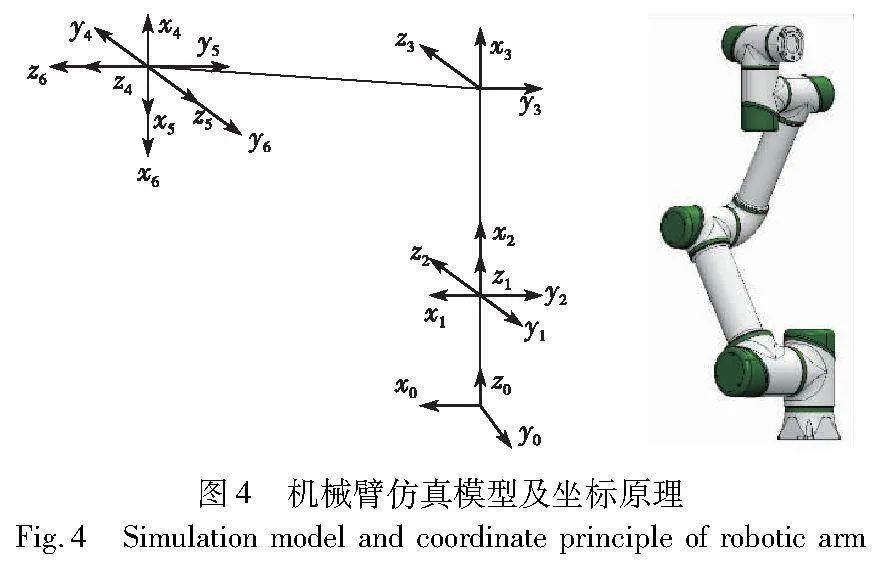
本文以中科深谷自主搭建的实验平台六轴机器人为仿真对象,基于改进D-H法建立六轴机械臂的坐标系及仿真模型如图4所示。
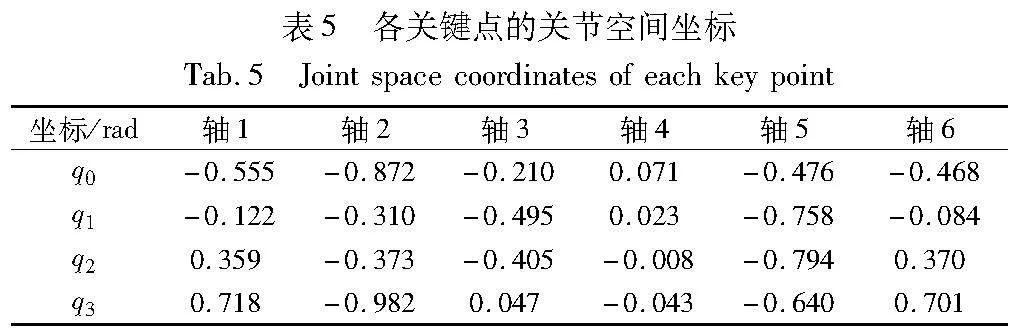
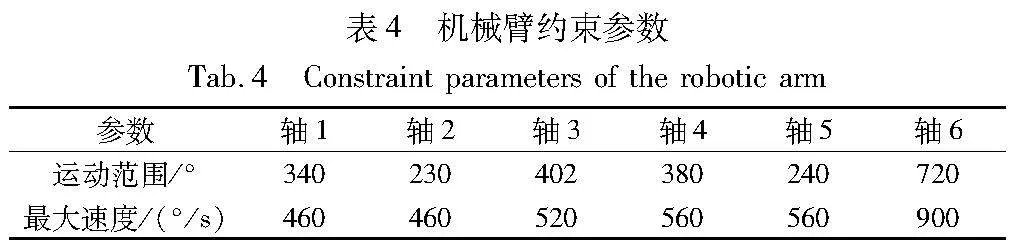
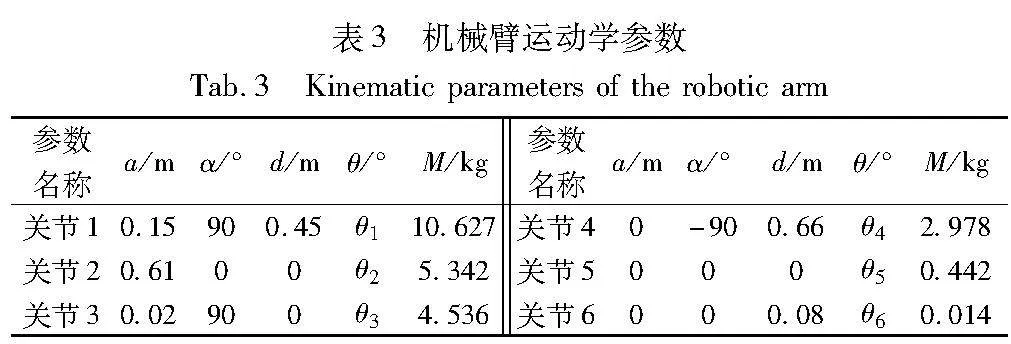
机械臂的运动学参数如表3所示,其中a表示连杆长度,α表示连杆扭转角,d表示连杆偏置,θ为关节变量,M为连杆质量。机械臂各轴的约束参数如表4所示。通过逆运学计算得到机械臂所经过的关键点关节坐标如表5所示,其中q0,q1,q2,q3分别为机械臂所经过的第一、第二、第三、第四个点的坐标。
4.2 仿真结果及分析
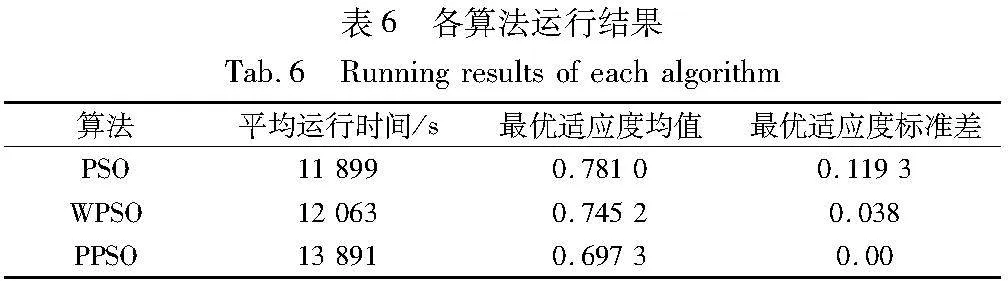
设定求解优化轨迹的粒子群算法的种群规模N均为50,最大迭代次数maxgen均为100,基本粒子群算法的权重系数ω 设为1,学习因子c1=c2=c3=2。为了更好地对比分析各粒子群算法在实际问题中的性能并减少随机性,各粒子群算法皆运行10次,得到各粒子群算法的结果如表6所示。
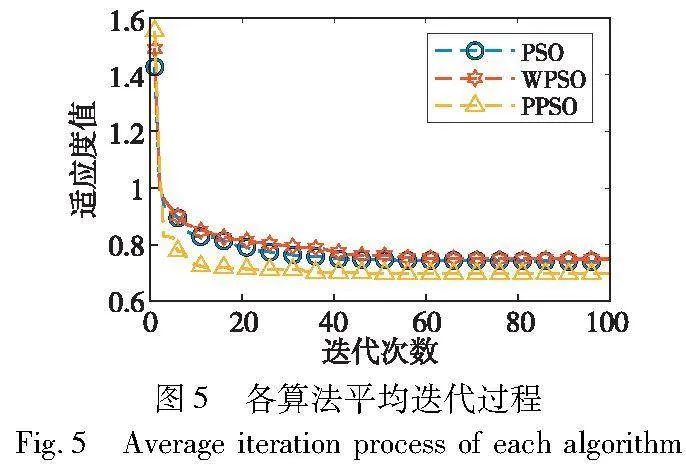
由表6可知,10次运行后,PPSO相较PSO和WPSO,其优化能力分别提升10.72%和6.43%,运行速度则分别降低14.3%和13.2%,其优化结果分别降低10.72%和6.43%。并且得了到各算法的平均迭代过程,如图5所示。
由图5可知,PPSO由于引入金字塔式的拓扑结构和PS因子,从而得到了更优的解,并且迭代次数也明显小于其他算法,而其他两种算法则在70次后陷入了局部最优。实验结果证明了PPSO的性能明显优于PSO和WPSO。
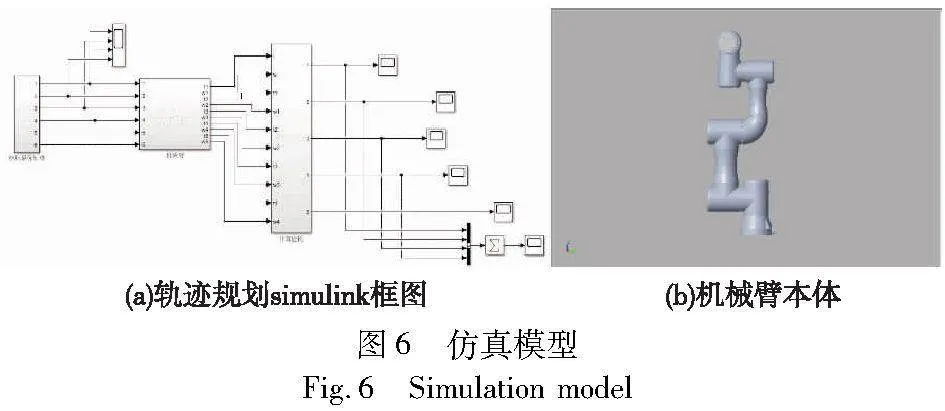
为了验证求得的能耗最优轨迹在机械臂上的有效性,在simscape环境下搭建如图6所示的仿真模型。
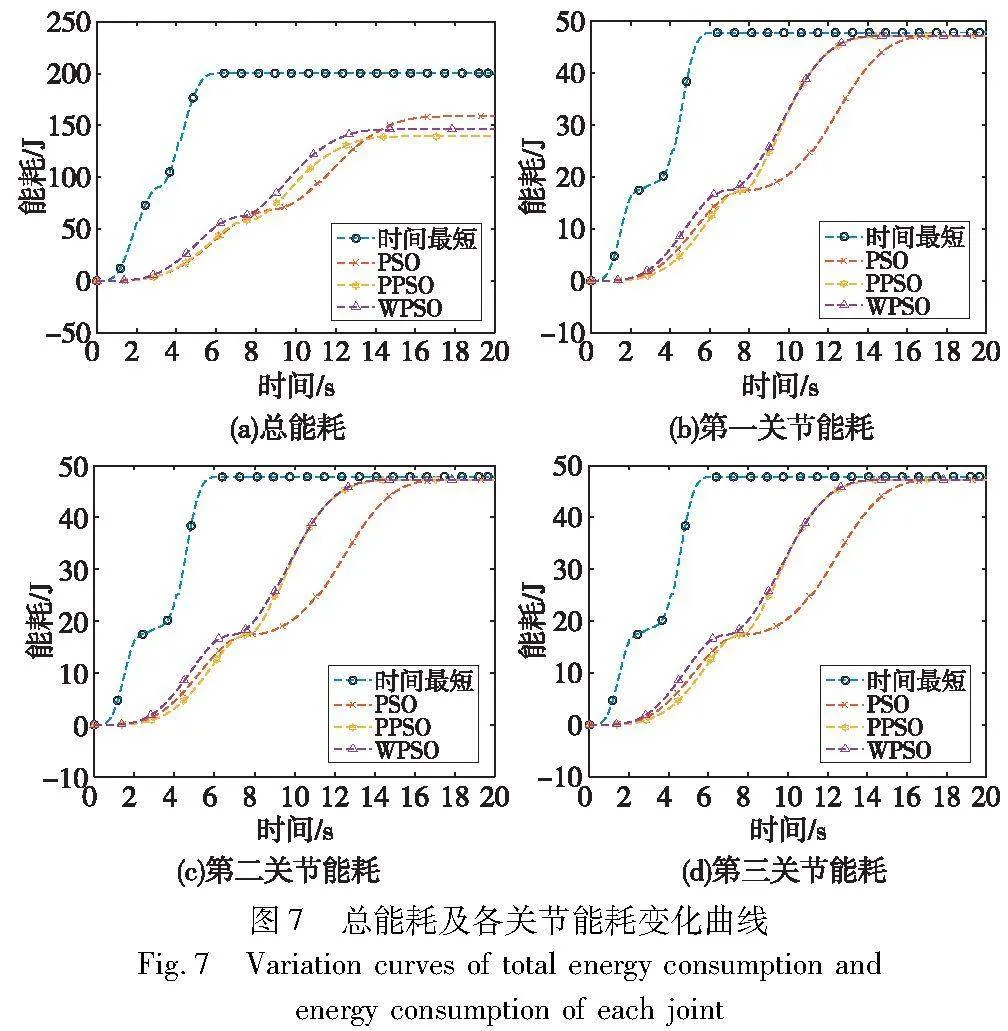
将得到的最优轨迹在仿真模型中进行可视化的仿真实验,得到如图7所示的机械臂前三关节能耗及总能耗的对比。
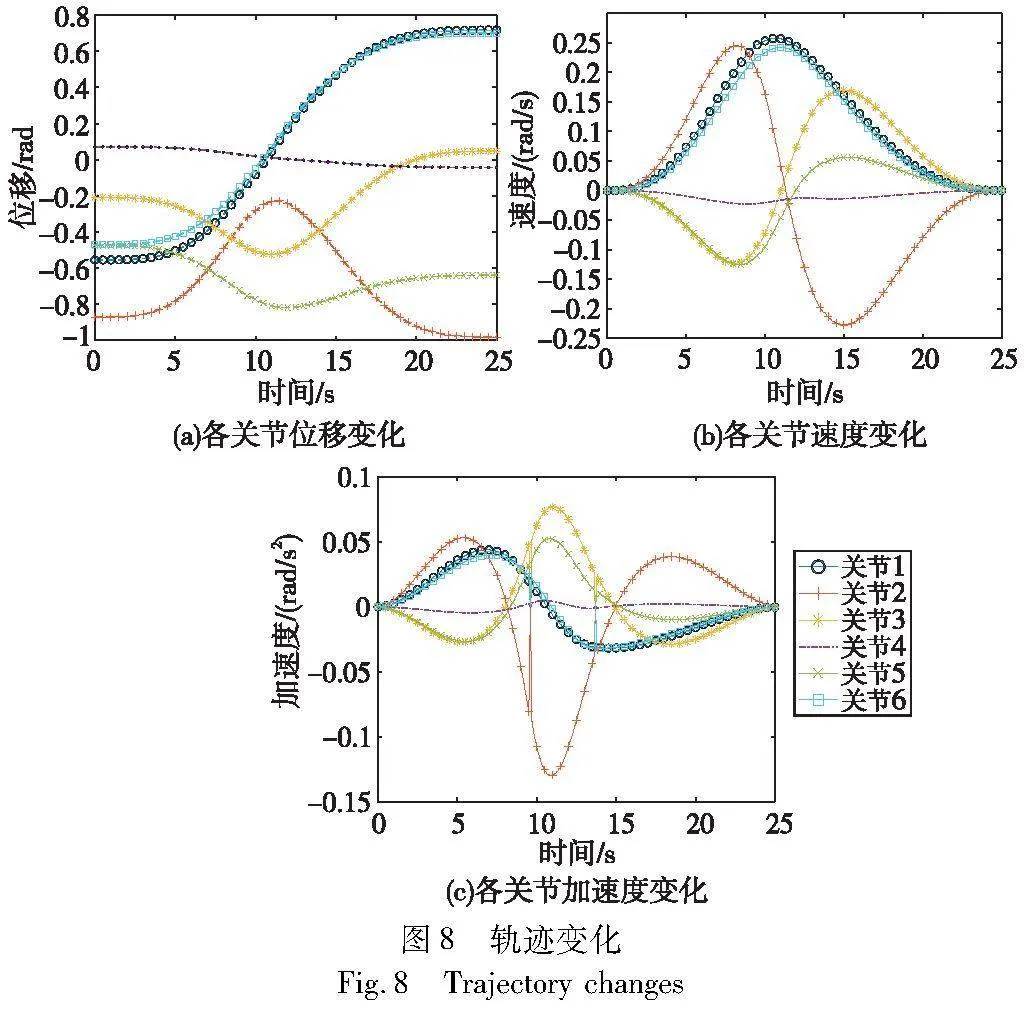
从图7中可以得知,自适应粒子群算法求得的轨迹的能耗相比基本粒子群、改进粒子群及时间最短轨迹分别降低5.9%、4.8%和 30.56%。由于时间最短轨迹仅考虑机械臂在工作中的效率因素,导致机械臂在短时间内引起较大的速度变化,使得能耗明显大于最优轨迹能耗,进一步得到由PPSO计算得到的最优轨迹变化如图8所示。
5 结束语
本文针对工业机器人能耗轨迹优化问题,作出了如下改进:通过五次多项式在机器人的关节空间中分段规划轨迹,从而使轨迹更加平滑;将金字塔式层的拓扑结构以及胜利百分比引入粒子群算法,用于求解最优轨迹。由仿真实验得到如下主要结论:
a)计算结果表明,PPSO的寻优能力相较PSO、WPSO分别提高10.7%和6.1%。运行速度虽然分别降低了14.3%和13.2%,但PPSO得到的10次结果几乎没有波动,稳定性出色。
b)通过仿真实验,PPSO得到的最优轨迹的能耗相较PSO、WPSO求解得到的轨迹及时间最短轨迹的能耗分别降低5.9%、4.8%和30.56%,并且各关节轨迹满足机械臂的约束条件,由此证明了该轨迹优化方法的可行性。
参考文献:
[1]国务院. 国务院关于印发《中国制造2025》的通知 [EB/OL]. (2015-05-08) [2021-02-12]. https://www.gov.cn/zhengce/zhengceku/2015-05/19/content_9784.htm. (State Council. Notice of the State Council on Issuing “Made in China 2025”[EB/OL]. (2015-05-08) [2021-02-12]. https://www.gov.cn/zhengce/zhengceku/2015-05/19/content_9784.htm.)
[2]安凯,马佳光. 基于变分法的三关节机械臂能耗最小路径规划 [J]. 光电工程,2015,42(9):48-54.(An Kai,Ma Jiaguang. Mini-mum energy consumption path planning of three-joint manipulator based on variational method [J]. Optoelectronic Engineering,2015,42(9): 48-54.)
[3]贺莹,梅江平,孙玉德,等. MD1200-YJ码垛机器人低能耗轨迹优化 [J]. 制造技术与机床,2020(8):95-101.(He Ying,Mei Jiang-ping,Sun Yude,et al. Low-energy trajectory optimization of MD1200-YJ palletizing robot [J]. Manufacturing Technology and Machine Tools,2020(8): 95-101.)
[4]贾文友,江磊,曹紫阳,等. 能耗约束优化工业机器人作业轨迹 [J]. 计算机工程与应用,2021,57(15): 245-250. (Jia Wenyou,Jiang Lei,Cao Ziyang,et al. Energy consumption constrained optimization of industrial robot operation trajectories [J]. Computer Engineering and Applications,2021,57(15): 245-250.)
[5]邓乾旺,罗正平,张丽科,等. 点焊机器人轨迹能耗模型及其优化算法研究 [J]. 中国机械工程,2016,27(1): 14-20. (Deng Qianwang,Luo Zhengping,Zhang Like,et al. Research on spot welding robot trajectory energy consumption model and its optimization algorithm [J]. Chinese Mechanical Engineering,2016,27(1): 14-20.)
[6]Chai Runqi,Tsourdos A,Savvaris A,et al.Solving constrained trajectory planning problems using biased particle swarm optimization[J]. IEEE Trans on Aerospace and Electronic Systems,2021,57(3):1685-1701.
[7]Lu Shaotian,Zhao Jingdong,Jiang Li,et al. Solving the time-jerk optimal trajectory planning problem of a robot using augmented Lagrange constrained particle swarm optimization [J]. Mathematical Problems in Engineering,2017,2017: article ID 1921479.
[8]Deng Yi,Zhou Tao,Zhao Guojin,et al. Energy saving planner model via differential evolutionary algorithm for bionic palletizing robot [J]. Sensors,2022,22(19): 7545.
[9]Saravanan R,Ramabalan S,Balamurugan C. Evolutionary optimal trajectory planning for industrial robot with payload constraints [J]. International Journal of Advanced Manufacturing Technology,2008,38(11-12): 1213-1226.
[10]Li Mi,Chen Huan,Shi Xin,et al. A multi-information fusion “triple variables with iteration” inertia weight PSO algorithm and its application [J]. Applied Soft Computing,2019,84: 105677.
[11]谢美华,李艳武,葛棚丹. 自适应混合粒子群算法求解置换流水车间调度问题 [J]. 计算机应用研究,2023,40(11): 3241-3246,3253. (Xie Meihua,Li Yanwu,Ge Pengdan. Adaptive hybrid particle swarm algorithm for solving permutation flow shop scheduling problem [J]. Application Research of Computers,2023,40(11): 3241-3246,3253.)
[12]Ye Wenxing,Feng Weiying,Fan Suohai. A novel multi-swarm particle swarm optimization with dynamic learning strategy [J]. Applied Soft Computing,2017,61: 832-843.
[13]Zhang Xinming,Wang Xia,Kang Qiang,et al. Differential mutation and novel social learning particle swarm optimization algorithm [J]. Information Sciences,2019,480: 109-129.
[14]Laskar N M,Guha K,Chatterjee I,et al. HWPSO: a new hybrid whale-particle swarm optimization algorithm and its application in electronic design optimization problems [J]. Applied Intelligence,2019,49: 265-291.
[15]Karimi-Mamaghan M,Mohammadi M,Meyer P,et al. Machine lear-ning at the service of meta-heuristics for solving combinatorial optimization problems: a state-of-the-art [J]. European Journal of Ope-rational Research,2022,296(2): 393-422.
[16]Hosseini S,Hahn I. Energy-efficient motion planning for electrical drives [C]// Proc of IEEE Electrical Power and Energy Conference. Piscataway,NJ:IEEE Press,2018: 1-7.
[17]Wang Shijie,Tao Jianfeng,Jiang Qincheng,et al. Manipulator joint fault localization for intelligent flexible manufacturing based on reinforcement learning and robot dynamics[J].Robotics and Computer-Integrated Manufacturing,2024,86:102684.
[18]Mohsen S,Behrooz A,Roza D. Optimization of energy consumption in industrial robots,a review [J]. Cognitive Robotics,2023,3: article No.3.
[19]Shami T M,El-Saleh A A,Alswaitti M,et al. Particle swarm optimization: a comprehensive survey [J]. IEEE Access,2022,10: 10031-10061.
[20]Wu Xuan,Han Jizong,Wang Di,et al. Incorporating surprisingly popular algorithm and Euclidean distance-based adaptive topology into PSO[J].Swarm and Evolutionary Computation,2023,76:101222.
[21]Zhang Weizheng,Li Guoqiang,Zhang Weiwei,et al. A cluster based PSO with leader updating mechanism and ring-topology for multimodal multi-objective optimization [J]. Swarm and Evolutionary Computation,2019,50: 100569.
[22]Yao Chengyu,Zhao Zheyu,Chen Dongning,et al. Unidirectional dynamic topology hybrid force PSO algorithm and its applications in reliability optimization [J]. Journal of Mechanical Engineering,2017,53(10): 166-179.
[23]Li Taiyong,Shi Jiayi,Deng Wu,et al. Pyramid particle swarm optimization with novel strategies of competition and cooperation [J]. Applied Soft Computing,2022,121: 108731.
[24]Corentin B. Stability analysis and stabilization of linear symmetric matrix-valued continuous,discrete,and impulsive dynamical systems—a unified approach for the stability analysis and the stabilization of linear systems [J]. Nonlinear Analysis: Hybrid Systems,2022,46:1-47.
[25]Anbarasi M P,Kanthalakshmi S. Power maximization in standalone photovoltaic system: an adaptive PSO approach [J]. Soft Computing,2023,27(12): 8223-8232.
[26]Wu Guohua,Mallipeddi R,Suganthan P N. Problem definitions and evaluation criteria for the CEC 2017 competition on constrained real-parameter optimization [R]. Changsha: National University of Defense Technology,2017.
[27]张豪,王贤琳. 自适应惯性权重优化的粒子群算法 [J]. 智能计算机与应用,2023,13(9): 5-8. (Zhang Hao,Wang Xianlin. Particle swarm algorithm for adaptive inertia weight optimization [J]. Intelligent Computers and Applications,2023,13(9): 5-8.)
[28]Liu Hao,Zhang Xuwei,Tu Liangping. A modified particle swarm optimization using adaptive strategy [J]. Expert Systems with Application,2020 (8): 152.
[29]Parsopoulos K E,Vrahatis M N. A unified particle swarm optimization scheme [C]//Proc of International Conference of Computational Methods in Sciences and Engineering. 2019: 868-873.
[30]Wu Jieyong,Song Chenxing. A distance evolution nonlinear PSO algorithm for energy-efficient path planning in 3D UASNs[J].IEEE Access,2019,7:105514-105530.
[31]Singh G,Singh A. A hybrid algorithm using particle swarm optimization for solving transportation problem [J]. Neural Computing and Applications,2020,32(15): 11699-11716.
[32]Xia Xuewen,Tang Yichao,Wei Bo,et al. Dynamic multi-swarm particle swarm optimization based on elite learning [J]. IEEE Access,2019,7: 184849-184865.
[33]Shen Ling,Zhang Zhe,Song Xiaoling,et al. A hybrid GA-PSO algorithm for seru scheduling problem with dynamic resource allocation [J]. International Journal of Manufacturing Research,2023,18(1): 100-124.

