数值仿真工具在“机械振动学”课程教学中的应用

摘要：随着科学技术发展，数值仿真模拟为抽象理论知识的学习及应用提供了可视化、低成本、高效率之新途径。基于ABAQUS有限元软件，以复杂服役环境下DF17导弹振动抑制为工程背景，以梁的横向振动模态为研究对象，分别模拟计算五种常见梁的前三阶横向振动固有频率及振型。与理论推导结果对比，进行误差分析，验证梁模型的适用条件。数值仿真模拟与理论学习的有机结合将有效强化学生对振动基本理论的理解，提高先进工具应用能力和问题分析能力。

关键词：数值仿真；机械振动；课程教学；模态分析

中图分类号：G642文献标识码：A

一、概述

从中国制造世界最大推力70吨级振动台，到实现世界最大单体隔震建筑——北京大兴国际机场的运营，可以知道，振动是影响高端装备、土木建筑等安全性与可靠性的关键因素，也是工程设计及应用中最具挑战性的核心对象。“机械振动学”理论学习及运用对航空航天、机械工程、土木工程等领域发展举足轻重［1］。

“机械振动学”作为部分工程类专业基础课程，系统地阐述了振动的基本理论与分析方法［23］。由于该课程具有内容广泛、理论抽象、公式繁多等特点，且学生已习惯在静力学框架下分析问题，在动力学理论学习过程中普遍反映知识抽象、理解困难。振动实验是辅助学生理解知识和实践应用最行之有效的方法，但通常学时有限且成本较高。随着科学技术发展，数值仿真模拟为抽象理论知识的学习及应用提供了可视化、低成本、高效率之新途径［45］。

本文以弹性体梁的横向振动为例，应用数值仿真工具辅助理论教学。DF17导弹作为高超声速、极高精度制导武器，复杂服役环境下振动抑制尤为重要。在实际飞行过程中，其振动形式是非常复杂的，涉及横向、轴向、扭转等多种振动耦合。在本科阶段振动基本理论教学中，可将该研究对象简化成欧拉伯努利梁模型进行解耦分析。下面基于梁横向固有振动模态开展理论分析与数值模拟。

二、梁横向振动模态理论推导

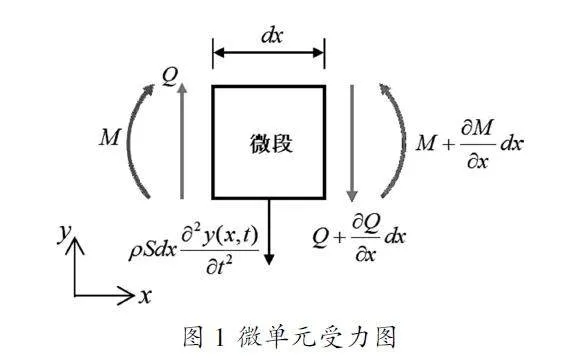
梁横向振动过程满足线弹性体基本假设和材料力学平面假设，只考虑梁的弯曲变形，不计剪切变形及转动惯量影响［3］。取微段受力分析，如图1所示，y（x，t）表示距原点x处截面在t时刻的横向位移，ρ为单位体积梁质量，S为梁横截面积，Q和M分别为截面上剪力和弯矩。

图1微单元受力图

根据牛顿第二定律得自由振动方程：

ρS2y（x，t）t2+Qx=0（1）

由于忽略截面转动影响，以右截面上任一点为矩心，由力矩平衡得：

Q=Mx（2）

根据材料力学的等截面假设，由弯矩与挠度的关系得：

M=EI2y（x，t）x2（3）

其中，E为弹性模量，I为截面对中性轴的惯性矩。将式（3）代入自由振动方程式（1）得：

2x2［EI2y（x，t）x2］+ρS2y（x，t）t2=0（4）

根据分离变量法，梁的主振动可假设为：

y（x，t）=φ（x）q（t）=φ（x）asin（ωt+θ）（5）

其中，ω为固有频率，θ为相位角。将式（5）代入式（4）得：

（EIφ″）″-ω2ρSφ=0（6）

对于等截面梁横向振动的振型函数一般形式为：

φ（x）=C1cosβx+C2sinβx+C3coshβx+C4sinhβx（7）

其中，系数C1～C4由边界条件确定，β为4ω2ρS/EI。

因此，梁的主振动表达为：

y（x，t）=（C1cosβx+C2sinβx+C3coshβx+C4sinhβx）asin（ωt+θ）

（8）

对简支梁边界条件，两端挠度和截面弯矩为零，即：

φ（0）=0，φ″（0）=0，φ（l）=0，φ″（l）=0（9）

分别代入式（7）得频率方程：

sinβl=0（10）

因此：

βil=iπ，i=1，2，3…（11）

固有频率为：

ωi=（iπl）2EIρS，i=1，2，3…（12）

振型函数为：

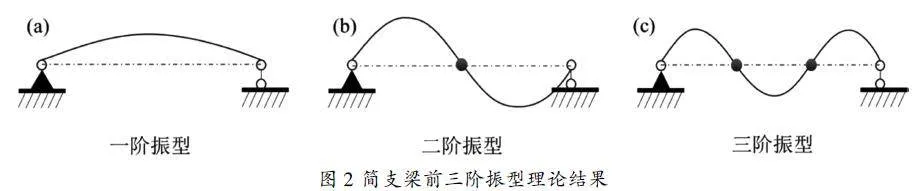
φi（x）=siniπlx，i=1，2，3…（13）

简支梁前三阶振型如图2所示。对于其他简单支承边界条件梁，模态计算流程同简支梁一致。不同梁横向振动边界条件及频率方程汇总如表1所示，可知各频率方程包含双曲函数，计算相应特征根非常复杂，模态分析更为困难。此时，编程计算及数值仿真则体现出显著优势。

三、梁横向振动模态有限元计算

利用ABAQUS有限元（FEM）软件对上述理论分析中的简支梁、自由梁、固定梁、悬臂梁和简支—固定梁分别进行横向振动模态仿真。基于DF17导弹进行缩比建模，简化为长（l）为300mm，直径（d）为20mm的圆截面梁。材料假定为钢材，密度7800kg/m3，弹性模量200×109Pa，泊松比0.3。采用梁单元网格划分，每个单元最大线长2mm。对于固定端，约束X、Y、Z、XR、YR、ZR六个自由度；对于固定简支端，约束X、Y、Z、XR、YR五个自由度；对于移动简支端，约束Y、Z、XR、YR四个自由度；对于自由端，不约束自由度。其中，自由度X、Y和Z表示三个方向轴向位移，XR、YR和ZR表示绕X、Y、Z轴向转动。各模型在线性摄动下以一定的频率进行振动。

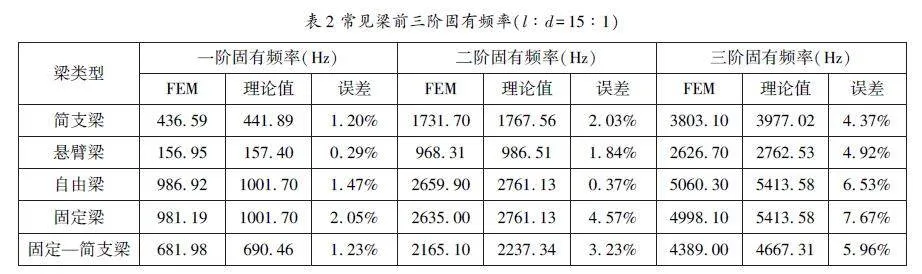
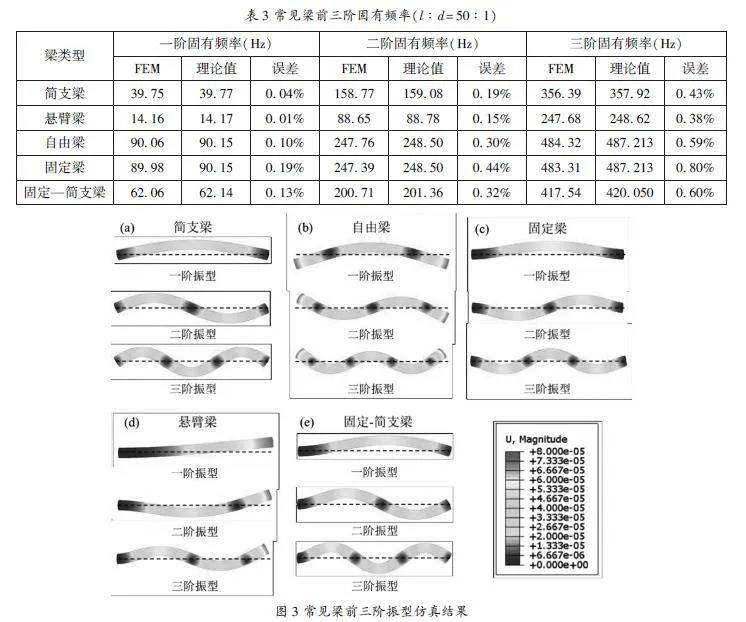
五种梁前三阶固有频率数值仿真结果汇总如表2所示，发现该条件下FEM方法得到的固有频率与理论计算结果较为接近，但仍存有一定误差，最大为7.67%。由“机械振动学”理论可知，欧拉伯努利梁模型仅适用于细长梁。随着增加有限元模型长径比，误差逐渐减小。当长径比调整至50∶1时，误差可控制在1%以内（表3），验证了梁模型的适用条件。相应的前三阶振型如图3所示。从振型仿真结果可直观看到与理论推导振动模态一致。通过有限元数值仿真的实践，不仅可以强化学生对理论知识的理解，还可以锻炼学生应用先进工具的能力以及分析问题、解决问题的能力。

结语

数值仿真方法能够快速直观获取分析结果，是辅助理论教学的重要手段。本文基于简支梁、悬臂梁、自由梁、固定梁、固定—简支梁五种常见梁的横向固有振动模态开展理论分析与ABAQUS有限元数值仿真，通过不同梁前三阶固有频率和振型的对比以及误差分析，实现了理论与实践的有机结合，有效帮助学生对抽象理论知识的理解及应用。

参考文献：

［1］黄修长，张振果，华宏星.以国家重大需求为引导的课程思政建设—以“机械振动学”课程为例［J］.教育教学论坛，2023，15：4952.

［2］黄修长，华宏星.国外最新振动学教材调研及特色分析［J］.力学与实践，2022，44（04）：960968.

［3］郑兆昌主编.机械振动［M］.北京：机械工业出版社.1980.

［4］余翔，王钰轲，李忠旭.“现代数值分析方法”课程教学的改革与实践［J］.教育教学论坛，2023，20：6063.

［5］罗靓，吕辉，肖冲，等.有限元法在“工程结构”本科课程教学的应用与实践［J］.南昌航空大学学报（自然科学版），2023，37（02）：101108.

基金项目：河北省高等教育教学改革研究与实践项目：基于机—材—力跨学科人才培养的点阵化科教融合探索与思政案例库建设（2022GJJG053）；河北工业大学本科教育教学改革研究与实践项目国际教育研究专项：本土国际化背景下专业课思政教学的探索与实践——以《机械振动》课程为例（GJZ202202002）；河北省新工科研究与实践项目：双向融合新工科建设国际化人才培养模式与机制研究（2020JXGK004）

作者简介：俎群（1989—），女，山东滨州人，博士，副教授，主要从事多尺度动力学数值仿真研究。