考虑碳减排的共燃发电厂鲁棒可信性选址决策优化

DOI：10.3969/j.issn.10001565.2024.04.003

摘要：基于“碳达峰、碳中和”战略目标，研究考虑碳减排的共燃发电厂选址决策问题．受天气状况、市场环境等外部因素的影响，生物质供应能力和生物质价格等参数具有不确定性，构造一个非精确可能性分布集来描述问题中的不确定参数，进而建立一个分布鲁棒可信性选址优化模型．通过推导鲁棒可信性目标和鲁棒可信性约束的等价形式，将原模型重构为一个可计算的混合整数线性规划模型．最后利用算例分析验证提出方法的有效性．

关键词：共燃发电厂选址；碳减排；非精确可能性分布集；分布鲁棒可信性优化

中图分类号：T818文献标志码：A文章编号：10001565（2024）04035510

Optimizing robust credibility location decision of co-firing power

plants considering carbon emission reduction

CHEN Aixia1，CHEN Airu2， LIANG Zhiyong3

（1. College of Mathematics and Information Science， Hebei University， Baoding 071002， China;

2. School of Management， Hebei University， Baoding 071002， China;

3. Hebei Information Engineering School， Baoding 071000， China）

Abstract： Based on the strategic goal of carbon peak and carbon neutrality， this paper studies the decision-making problem of co-firing power plant location considering carbon emission reduction. Due to the influence of weather conditions， market environments and other external factors， the parameters such as biomass supply capacity and biomass price are uncertain. To address this problem， this paper constructs an ambiguity set of possibility distributions to characterize the uncertain parameters， and then proposes a distributionally robust credibility location optimization model. The original model is reformulated as a computable mixed-integer linear programming model by deriving the equivalent forms of robust credibility objective and robust credibility constraint. Finally， the effectiveness of the proposed method is demonstrated by an example.

Key words： co-firing power plant location; carbon emission reduction; an ambiguity set of possibility distributions; distributionally robust credibility optimization

收稿日期：20231114;修回日期：20240221

基金项目：河北省社会科学基金资助项目（HB23GL019）

第一作者：陈爱霞（1982—），女，河北大学讲师，博士，主要从事模糊优化、鲁棒优化等方向研究．

E-mail：chenaixia@hbu.edu.cn

2021年全球能源燃烧产生的CO2高达36.3 Gt，其中燃煤发电产生的CO2约占全球CO2排放总量的30%［1］．世界上2/3的电力是由煤电行业产生的，直到2035年，煤炭仍将是最主要的电力来源［2］．为了应对全球气候变化和实现环境保护需求，煤电行业迫切需要实施节能减排计划．与其他碳减排技术相比，生物质-煤共燃发电技术由于价格相对低廉且具有负碳或零碳排放效应，是煤电行业实现碳减排目标的可行途径［3］．因此，在中国提出“碳达峰、碳中和”战略目标的背景下，在现有燃煤发电厂中选择一些建设为生物质-煤共燃发电厂对于解决煤电行业碳排放超标的问题至关重要．

关于生物质发电厂的选址决策问题，大量研究通过建立数学模型来求解，模型中通常以最小化总成本为目标函数．Biberacher等［4］提出一个数学模型，在由生物质生长率和运输系统的状态共同决定的理想生物质供应区域内确定最佳的发电厂位置．Bojic等［5］采用p-中值模型，通过最小化生物质运输成本的总和来确定发电厂的位置．Jayarathna等［6］首先基于模糊多标准分析法确定各个地点的适宜性，然后建立一个选址分配模型来确定生物质能源工厂的最佳位置．刘喆轩等［7］建立一个基于多目标优化的多周期生物燃料供应链模型来优化生物质产地、生物质能源工厂、生物燃料市场等选址决策．还有一些研究同时将经济和环境因素纳入生物质发电厂选址问题的建模之中，如Idris等［8］、Martínez等［9］和Karimi等［10］.上述研究大多数在确定环境下对生物质发电厂选址问题进行研究．

在复杂多变的外界环境中，不确定性无处不在．目前，鲁棒优化和随机规划等不确定性优化方法已广泛应用到该问题的研究中． Ahmadvand 等 ［11］ 建立一个同时考虑生物质供应链的年度成本和碳排放量的双目标鲁棒优化模型．随后，Aranguren等［12］提出一个双目标2阶段随机规划模型，用于考虑温室气体排放的大规模生物质共燃供应链设计．在不确定优化方法中，模糊规划更适合处理认知上的不确定性，即主观不确定性． Nayeri等［13］提出了一个具有运输成本、碳排放能力等不确定性的模糊优化模型，旨在优化相互冲突的社会、环境和经济目标．Ilbahar等［14］开发了一个模糊线性规划模型来处理资源可用性约束的非精确性．上述研究假设不确定参数的分布信息是准确已知的，然而，由于历史数据的有限性或决策者认知上的不足，通常难以获得准确的可能性分布．当一个不确定参数的分布不能准确获得时，其分布是非精确的，通常采用一个非精确分布集来描述．此时，在分布鲁棒可信性优化的框架下［15］，基于最差情形准则，对分布不确定性进行建模．分布鲁棒可信性优化方法目前已经应用于许多实际问题，例如物资预置问题［16］、项目选择问题［17］等．

综上所述，现有的生物质发电厂选址问题研究在建模方法方面已经取得诸多的研究成果，丰富了生物质供应链管理问题的研究．然而，通过文献分析，发现现有研究的局限性如下：1）大量研究采用确定性优化方法进行研究．在复杂多变的外部环境下，当某个参数的取值发生波动时，当前最优决策的执行效果可能会很差；2）在不确定性的相关研究中，大多数学者只考虑供应能力、价格等不确定参数中的某一个不确定参数；3）文献中通常假设这些不确定参数的概率分布或可能性分布是完全已知的．针对不足，本文构造了一类非精确可能性分布集，用以描述生物质供应能力和生物质价格等参数的分布不确定性，进而采用分布鲁棒可信性优化方法对考虑碳减排的共燃发电厂选址问题进行建模研究．

1问题描述

二级生物质供应链包括生物质供应商和燃煤发电厂（即候选的共燃发电厂），其中生物质供应商负责收集指定范围内的生物质并进行预处理，以便于运输到共燃发电厂．在碳减排政策下，决策者需要做出将哪些燃煤发电厂建设为生物质-煤共燃发电厂，并确定建设规模、生物质供应商和共燃发电厂之间的生物质运输量等决策．

在对共燃发电厂的选址和规模进行决策时，决策者通常将总成本最小化作为目标函数．考虑到生物质共燃发电方式需要对原有的物料搬运系统、锅炉系统等设施进行改造，因此会产生一定的固定成本．然而，设备改进的成本随着生物质在共燃策略中的比例不同而变化，将其简化为3种共燃发电厂规模，即大、中和小3种规模，分别对应不同的固定改造成本．此外，由于农业、林业生物质的分散性，运输成本是总成本中的重要组成部分．从环境因素考虑，由于在共燃策略中，一定数量的煤被生物质替代后，相应的碳排放量必然会减少，这使得共燃发电厂可以更好地实现政府下达的碳减排目标．为了对考虑碳减排的共燃发电厂选址问题进行建模，首先做出如下假设：

1）本文关注的是供应不确定的情况下生物质共燃发电厂的选址问题，因此没有考虑生物质的采集和收集过程．

2）供应商对收集的生物质进行预处理，并将处理费用加到生物质价格中，因此没有考虑生物质的预处理成本．

3）由于本文考虑的运营周期是年度的，生物质供应商的年度供应能力很大．与之相比，生物质运输过程中的损失量可以忽略不计．

4）由于生物质分布分散、体积大、密度低等特点，因此本文仅考虑大型卡车一种运输方式．

5）共燃发电厂燃烧生物质所产生的碳排放量与生物质生长过程中吸收的碳相抵消［18］．

2模型建立

在考虑碳减排的共燃发电厂选址问题中，由于洪水、干旱、病虫害防治、设备故障等因素的影响，生物质供应能力和生物质价格等参数都是不确定的．由于历史数据有限，通常无法获得这些不确定参数的准确分布，只能通过专家的主观估计或推断来获得其部分分布信息（如名义可能性分布）．此时，与其他不确定优化技术相比，模糊规划更适合对该问题进行建模，因为能够更好地表征不确定参数的主观不确定性．

2.1鲁棒可信性约束

令供应商i为共燃发电厂j提供的生物质数量为yij，则每个供应商所提供的生物质总量不能超过其供应能力ξi，即∑j∈［J］yij≤ξi，i∈［I］.（1）由于诸多现实因素的影响，当ξi具有不确定性时，很难保证这一约束成立．已知ξi的可能性分布表示为μξi，令该约束成立的可信性大于等于给定的可信性水平αi，建立可信性约束：Cr∑j∈［J］yij≤ξi≥αi，i∈［I］，（2）其中，Cr表示可信性测度．

由于可用数据的有限性，μξi通常无法准确确定，假设其属于非精确分布集δξi．基于最差情形准则，将上述可信性约束建模为以下鲁棒可信性约束：infμξi∈δξiCr∑j∈［J］yij≤ξi≥αi，i∈［I］.（3）2.2鲁棒可信性目标

由于生物质价格ζi的可能性分布μζi是不确定的，令可变分布μζi属于非精确分布集δζi，则采购成本的期望表示为Eμζi∑i∈［I］∑j∈［J］yijζi，μζi∈δζi.（4）基于最差情形准则，共燃发电厂选址问题的目标函数表示为最小化最差情形下的总成本，∑j∈［J］∑l∈［L］xjlhjl+∑j∈［J］∑l∈［L］xjlgjl+∑i∈［I］∑j∈［J］yijdijHt+supμζi∈δζiEμζi∑i∈［I］∑j∈［J］yijζi，（5）其中：xjl是二元决策变量，若将燃煤发电厂j建设为规模l的共燃发电厂，则xjl为1，否则为0；hjl和gjl分别表示在位置j建造规模l的共燃发电厂所需的年度固定成本和年度运营成本；dij表示供应商i和共燃发电厂j之间的距离；Ht表示单位运输成本．

综上所述，针对考虑碳减排的共燃发电厂选址问题，本文建立了一个分布鲁棒可信性优化 （DRCO）模型 如式（3）、（6）～（12）所示：minxjl，yij ∑j∈［J］∑l∈［L］xjlhjl+∑j∈［J］∑l∈［L］xjlgjl+∑i∈［I］∑l∈［J］yijdijHt+supμζi∈δζiEμζi∑i∈［I］∑j∈［J］yijζi，（6）

s.t.约束（3），

∑l∈［L］xjl≤1，j∈［J］，（7）

∑j∈［J］∑l∈［L］xjl=n，（8）

∑j∈［J］∑l∈［L］xjlQlTr-∑i∈［I］∑j∈［J］yijTc-∑i∈［I］∑j∈［J］yijTs≥Cap，（9）

∑i∈［I］yijρi≥∑l∈［L］Qlxjl，j∈［J］，（10）

xjl∈{0，1}，j∈［J］，l∈［L］，（11）

yij≥0，i∈［I］，j∈［J］，（12）DRCO模型中：式（6）是鲁棒可信性目标；约束（7）保证在每个燃煤发电厂最多建设一种规模的共燃装置；约束（8）给定共燃发电厂的建设总数为n；约束（9）中，Ql表示规模为l的共燃发电厂中煤的替代量，Tr表示燃烧1×104 t煤所产生的碳排放量，Tc表示预处理1×104 t生物质所产生的碳排放量，Ts表示运输1×104 t生物质所产生的碳排放量，Cap表示整个地区所产生的碳减排量的最小值；约束（10）中，ρi表示供应商i提供的生物质的能量转化系数，约束（10）表示每个发电厂获得的生物质总量不小于其需求量．最后，约束条件（11）和（12）分别定义了二元和连续决策变量．

鲁棒可信性目标（6）包含无穷个期望值，且鲁棒可信性约束（3）包含无穷多个可信性约束，因此建立的DRCO模型是半无限规划模型，无法直接求解．因此本文将建立的DRCO模型重构为计算上可处理的鲁棒对等模型．

3模型重构

3.1非精确可能性分布集的构造

通过在名义可能性分布的附近引入线性扰动项，构造一个非精确可能性分布集来描述生物质供应能力和生物质价格的分布不确定性．

假设模糊变量ξ的名义可能性分布μ0～Tra（r1，r2，r3，r4），其中-∞lt;r1lt;r2≤r3lt;r4lt;+∞，令θl，θr∈［0，1］，则ξ的非精确可能性分布集构造如下：δξ（r1，r2，r3，r4;θl，θr）={μξ（r，λ1，λ2）=μ0（r）+λ1μ1（r）+λ2μ2（r），λ1，λ2∈［-θl，θr］}，（13）其中：（λ1，λ2）是波动向量;［-θl，θr］×［-θl，θr］是波动集.基本波动μ1（r）和μ2（r）定义如下：μ1（r）=min{μ0（r），1-μ0（r）}，r∈［r1，r2］，0，其他.

μ2（r）=min{μ0（r），1-μ0（r）}，r∈［r3，r4］，0，其他.特殊地，当θl=θr=0时，非精确分布集δξ（r1，r2，r3，r4;θl，θr）退化为ξ的名义可能性分布．

3.2鲁棒可信性目标和鲁棒可信性约束的等价形式

定理1 假设单位价格ζi（i∈［I］）的可能性分布属于非精确分布集δζi（rζi1，rζi2，rζi3，rζi4;θζil，θζir）．若ζi（i∈［I］）的名义可能性分布是相互独立的，则ζ=∑i∈［I］∑j∈［J］yijζi的可能性分布属于非精确分布集δζ（rζ1，rζ2，rζ3，rζ4;θζl，θζr），且supμζi∈δζi E∑i∈［I］∑j∈［J］yijζi=2（rζ1+rζ2+rζ3+rζ4）+θζl（rζ2-rζ1）+θζr（rζ4-rζ3）8，（14）其中：rζs=∑i∈［I］∑j∈［J］yijrζis（s=1，2，3，4）;θζl=maxi∈［I］ θζil;θζr=mini∈［I］ θζir．

证明：因为ζi（i∈［I］）的名义可能性分布是相互独立的，所以对于任意r∈［rζ1，rζ2］，存在rζi∈［rζi1，rζi2］（i∈［I］），使得Crζ=r=∑i∈［I］∑j∈［J］yijrζi=maxi∈［I］ Cr{ζi=rζi}．进一步分析，μζ（r，λ1，λ2）=μζ0（r）+λ1μζ1（r）+λ2μζ2（r），λ1，λ2∈［-θζl，θζr］，其中，μζ0～Tra（rζ1，rζ2，rζ3，rζ4），且rζs=∑i∈［I］∑j∈［J］yijrζs（s=1，2，3，4），θζl=maxi∈［I］ θζil，θζr=mini∈［I］ θζir．因此ζ=∑i∈［I］∑j∈［J］yijζi的可能性分布属于非精确分布集δζ（rζ1，rζ2，rζ3，rζ4;θζl，θζr）．

根据模糊变量的期望值公式［19］，可得线性组合ζ的鲁棒期望值．证毕．

定理2 若供应能力ξi（i∈［I］）的可能性分布属于非精确分布集δξi（rξi1，rξi2，rξi3，rξi4;θξil，θξir），则鲁棒可信性约束（3）等价于G（rξi1，rξi2，rξi3，rξi4;θξil，θξir;αi）≥∑j∈［J］yij，i∈［I］，（15）其中，G（rξi1，rξi2，rξi3，rξi4;θξil，θξir;αi）=rξi4-2αi（rξi4-rξi3）1-θξil，αi∈0，1-θξil4，rξi3+（1-2αi）（rξi4-rξi3）1+θξil，αi∈1-θξil4，12，rξi2-（2αi-1）（rξi2-rξi1）1-θξir，αi∈12，3-θξir4，rξi1+2（1-αi）（rξi2-rξi1）1+θξir，αi∈3-θξir4，1.

证明：已知ξi（i∈［I］）的可能性分布属于非精确分布集δξi（rξi1，rξi2，rξi3，rξi4;θξil，θξir），因此ξi（i∈［I］）的可能性分布如下：μξi（r，λ1，λ2）=（1+λ1）（r-rξi1）rξi2-rξi1，rξi1≤r≤12（rξi1+rξi2），（1-λ1）r+λ1rξi2-rξi1rξi2-rξi1，12（rξi1+rξi2）＜r≤rξi2，1，rξi2＜r≤rξi3，（λ2-1）r-λ2rξi3-rξi4rξi4-rξi3，rξi3＜r≤12（rξi3+rξi4），（1+λ2）（rξi4-r）rξi4-rξi3，12（rξi3+rξi4）＜r≤rξi4，其中，λ1，λ2∈［-θξil，θξir］．

进而，由可能性分布μξi（r，λ1，λ2）计算模糊事件{ξi≥r}的可信性为Cr{ξi≥r}=1，r＜rξi1，1-（1+λ1）（r-rξi1）2（rξi2-rξi1），rξi1≤r＜12（rξi1+rξi2），1-（1-λ1）r+λ1rξi2-rξi12（rξi2-rξi1），12（rξi1+rξi2）≤r＜rξi2，12，rξi2≤r＜rξi3，（λ2-1）r-λ2rξi3+rξi42（rξi4-rξi3），rξi3≤r＜12（rξi3+rξi4），（1+λ2）（rξi4-r）2（rξi4-rξi3），12（rξi3+rξi4）≤r＜rξi4，0，r≥rξi4.令r=12（rξi1+rξi2），则有Cr{ξi≥r}=3-λ14.考虑αi∈3-λ14，1，则有1-（1+λ1）（r-rξi1）2（rξi2-rξi1）=αi，于是（ξi）λsup，Cr（αi）=rξi1+2（1-αi）（rξi2-rξi1）（1+λ1）．其他情况类似可证．证毕．

3.3计算上可处理的鲁棒对等模型

基于定理1和定理2的结论，将DRCO模型重构为计算上可处理的鲁棒对等模型如下：minxjl，yij∑j∈［J］∑l∈［L］xjlhjl+∑j∈［J］∑l∈［L］xjlgjl+∑i∈［I］∑j∈［J］yijdijHt+π（rζ1，rζ2，rζ3，rζ4;θζl，θζr），

s.t.约束（7）-（12），（15），其中，π（rζ1，rζ2，rζ3，rζ4;θζl，θζr）=2（rζ1+rζ2+rζ3+rζ4）+θζl（rζ2-rζ1）+θζr（rζ4-rζ3）8．

可计算的鲁棒对等模型是一个混合整数线性规划模型，可由优化软件直接求解．

4数值算例

4.1算例描述

选取某市燃煤发电厂共燃建设决策问题作为数值算例．从该市选择16个具有秸秆压缩功能的预处理中心作为生物质供应商，并选择8个燃煤发电厂作为建设共燃发电厂的候选地点，其位置信息见表1．基于每个地点的经纬度，利用MATLAB软件计算出任意供应商和发电厂之间的距离．选取大型卡车作为运输工具，单位运输费用（元/（t·km-1））从区间［0.756，0.924］随机选取［13］．节约1×104 t标煤减少的CO2排放量为4 990 t，生物质运输过程中产生的单位碳排放量是1.553×10-4 t/（km·t），生物质预处理过程中每t产生的CO2是0.029 1 t［20］．共燃发电厂的建设规模分为大、中、小3种，相应的年固定成本分别为915万元，674万元和496万元；相应的年煤炭替换量分别为1.6×106、8×105和4×105 t．8个发电厂在不同共燃建设规模情况下的年运营成本见表2．能量转换系数从区间［0.553 5，0.676 5］随机选取［21］．各个供应商的生物质价格（元/t）和供应能力（104 t）的名义可能性分布见表3．

4.2计算结果

在数值实验中，将可信性水平αi（i∈［I］）设置为相同的α，碳减排下限为Cap=1.5×106．假设所建共燃发电厂的数量为4，求解结果如图1所示．由图1可知，随着可信性水平α的增加，最优值越来越大．这是因为α的增加使得DRCO模型的可行域减小，因此最优值（最小总成本）变大．同时，共燃发电厂建设个数的增加导致最优值变大．实际可以选择合适的共燃发电厂建设个数以及可信性水平，使得总成本符合决策者的资金预算．

当可信性水平α=0.85时，不同共燃发电厂建设个数下的最优选址和运输决策见表4．例如，n=5时，在位置P2、P5、P6、P7和P8建设共燃发电厂，规模分别为小、小、小、中、大．其中：生物质供应商S1和S10为P2运输生物质；供应商S4和S14为P5运输生物质；供应商S2和S14为P6运输生物质；S2、S7和S13为P7运输生物质；S1、S5、S6、S9、S11和S16为P8运输生物质．可以看出，共燃发电厂的规模与为其提供生物质的供应商数量有关．

4.3模型比较

为了验证提出的DRCO模型的有效性，将DRCO模型和名义分布模型比较．当价格和供应能力的可能性分布都准确已知，即为非精确分布集中的名义分布，得到名义分布模型．选取Cap=1.5×106，α=0.85，n=5，计算可得DRCO模型的最优值是3.590 55×109元，而名义分布模型的最优值是2.098 71×109元．可以看出，DRCO模型的最优值比名义分布模型的最优值大1.491 84×109元，这就是所谓的鲁棒代价．虽然DRCO模型的最优值比较大，即付出了鲁棒代价，但是DRCO模型得到的最优决策是稳健的，能够抵御分布的不确定性．

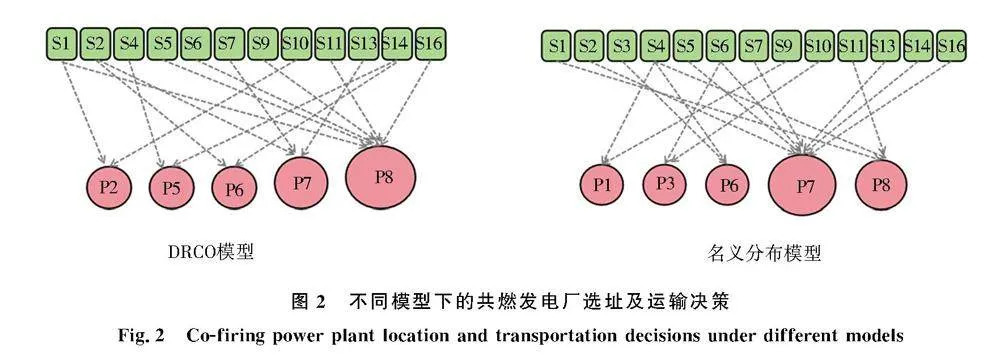
图2给出了DRCO模型和名义分布模型的最优决策，由图2知，2个不同模型得到的最优决策完全不同．DRCO模型的选址结果为P2、P5、P6、P7和P8，其规模分别为小、小、小、中、大；而名义分布模型的选址结果为P1、P3、P6、P7和P8，其规模分别为小、小、小、大、中．当供应能力和价格的可能性分布发生波动时，名义分布模型的最优解将不再是最优的，甚至是不可行的；而本文提出的DRCO模型的最优解对于非精确分布集内的任何可能性分布总是可行的，因此可以抵御分布的不确定性．当模糊变量的准确可能性分布无法确定时，DRCO模型是一个更好的选择．

5结论

研究了考虑碳减排的生物质-煤共燃发电厂选址决策问题．受洪水、干旱、病虫害等天气状况的影响，生物质供应能力和生物质价格等参数是不确定的.由于历史数据的有限性，很难准确获得这些不确定参数的可能性分布.基于此，本文首先构造了一个非精确可能性分布集来描述分布的不确定性，进而提出了共燃发电厂选址问题的分布鲁棒可信性优化模型．与名义分布模型相比，分布鲁棒可信性优化模型提供的最优决策可以抵御参数的分布不确定性．因此，当无法获得准确的可能性分布时，采用本文提出的分布鲁棒可信性优化方法可以提供一个更加稳健的共燃发电厂选址决策．

在实际运输中可能涉及公路、铁路、水路等多种运输方式，因此未来的研究中可以考虑多式联运或者不同车型组合对供应链成本的影响，进而选择经济有效的运输方式．

参考文献：

［1］International Energy Agency. Globalized energy review： CO2 emiesions in 2021［R］. France： IEA， 2022：3-4.

［2］王勇.碳排放是能源可持续发展的最大挑战—《BP2023年世界能源展望》摘要［J］.国际石油经济，2014，22（6）：22-27.

［3］KHADEMI A， EKSIOGLU S. Optimal governmental incentives for biomass cofiring to reduce emissions in the short-term［J］. IISE Trans， 2021， 53（8）： 883-896. DOI： 10.1080/24725854.2020.1718247.

［4］BIBERACHER M， TUM M， GNTHER K P， et al. Availability assessment of bioenergy and power plant location optimization： a case study for Pakistan［J］. Renew Sustain Energy Rev， 2015， 42： 700-711. DOI： 10.1016/j.rser.2014.10.036.

［5］BOJIC S， MARTINOV M， BRCANOV D， et al. Location problem of lignocellulosic bioethanol plant - Case study of Serbia［J］. J Clean Prod， 2018， 172： 971-979. DOI： 10.1016/j.jclepro.2017.10.265.

［6］JAYARATHNA L， KENT G， O’HARA I， et al. A Geographical Information System based framework to identify optimal location and size of biomass energy plants using single or multiple biomass types［J］. Appl Energy， 2020， 275： 115398. DOI： 10.1016/j.apenergy.2020.115398.

［7］刘喆轩，邱彤，陈丙珍.多期生物燃料供应链网络建模与多目标优化［J］.化工学报， 2014， 65（7）： 2802-2812. DOI： 10.3969/j.issn.0438-1157.2014.07.042.

［8］MOHD IDRIS M N， HASHIM H， RAZAK N H. Spatial optimisation of oil palm biomass co-firing for emissions reduction in coal-fired power plant［J］. J Clean Prod， 2018， 172： 3428-3447. DOI： 10.1016/j.jclepro.2017.11.027.

［9］MARTNEZ-GUIDO S I， ROS-BADRN I M， GUTIRREZ-ANTONIO C， et al. Strategic planning for the use of waste biomass pellets in Mexican power plants［J］. Renew Energy， 2019， 130： 622-632. DOI： 10.1016/j.renene.2018.06.084.

［10］KARIMI H， EK

瘙塁IOGˇLU S D， CARBAJALES-DALE M. A biobjective chance constrained optimization model to evaluate the economic and environmental impacts of biopower supply chains［J］. Ann Oper Res， 2021， 296（1）： 95-130. DOI： 10.1007/s10479-019-03331-x.

［11］AHMADVAND S， SOWLATI T. A bi-objective robust model for minimization of costs and emissions of syngas supply chain［J］. Comput Chem Eng， 2023， 179： 108404. DOI： 10.1016/j.compchemeng.2023.108404.

［12］ARANGUREN M F， CASTILLO-VILLAR K K. Bi-objective stochastic model for the design of large-scale carbon footprint conscious co-firing biomass supply chains［J］. Comput Ind Eng， 2022， 171： 108352. DOI： 10.1016/j.cie.2022.108352.

［13］NAYERI S， PAYDAR M M， ASADI-GANGRAJ E， et al. Multi-objective fuzzy robust optimization approach to sustainable closed-loop supply chain network design［J］. Comput Ind Eng， 2020， 148： 106716. DOI： 10.1016/j.cie.2020.106716.

［14］ILBAHAR E， KAHRAMAN C， CEBI S. Location selection for waste-to-energy plants by using fuzzy linear programming［J］. Energy， 2021， 234： 121189. DOI： 10.1016/j.energy.2021.121189.

［15］刘彦奎，刘颖.鲁棒可信性优化的新进展［J］.河北大学学报（自然科学版）， 2021， 41（5）： 457-462. DOI： 10.3969/j.issn.1000-1565.2021.05.002.

［16］白雪洁.应急物资预置问题的可信性优化模型［J］.数学的实践与认识， 2017， 47（14）： 267-276. DOI： CNKI：SOH：SSJS.0.017-14-029.

［17］刘颖，冯雪芹.能力导向下的模糊项目组合优化［J］.河北大学学报（自然科学版）， 2018， 38（4）： 346-355. DOI： 10.3969/j.issn.1000-1565.2018.04.002.

［18］CAMPBELL J E， LOBELL D B， FIELD C B. Greater transportation energy and GHG offsets from bioelectricity than ethanol［J］. Science， 2009， 324（5930）： 1055-1057. DOI： 10.1126/science.1168885.

［19］刘彦奎.可信测度论：一种处理主观不确定性的方法［M］.科学出版社， 2018.

［20］SAGHAEI M， GHADERI H， SOLEIMANI H. Design and optimization of biomass electricity supply chain with uncertainty in material quality， availability and market demand［J］. Energy， 2020， 197： 117165. DOI： 10.1016/j.energy.2020.117165.

［21］SUN R W， LIU T T， CHEN X D， et al. A biomass-coal co-firing based bi-level optimal approach for carbon emission reduction in China［J］. J Clean Prod， 2021， 278： 123318. DOI： 10.1016/j.jclepro.2020.123318.

（责任编辑：王兰英）