基于最小二乘原理及间接平差的变形监测控制网数据处理分析

摘 要：在某几何模型中，总的观测量为，必要观测量，选择t个必要观测量为参数，将每一个观测值表示成所选参数的函数，列立n个误差方程，这种以误差方程为函数模型的平差方法，称为间接平差法。在变形监测控制网数据处理中，通常可以采用基于最小二乘原理的间接平差法对网中的观测数据进行平差和点位精度分析，求出最弱点中误差、最弱边中误差、绘制误差椭圆。其中处理的关键是误差方程式的列立、非线性条件方程式线性化、误差方程式的求解及未知点精度评定。本文以在益阳市资江三桥布设的桥梁控制网为例，推导了全部的桥梁控制网解算过程，并得出了结论。

关键词：间接平差；法方程；最小二乘原理；线性方程组

Analysis of Data Processing for Deformation Monitoring Control Network Based on Least Squares Principle and Indirect Adjustment

Cao Yuanzhi1 Nie Zhiping1 Peng Zhihong1 Peng Zheng2

1.Hunan City University Institute of Municipal and Mapping Engineering Hunan Yiyang 413000 ；

2. Hunan Tunnel Engineering Corporation Hunan Yiyang 413000

Abstract： I In a certain geometric model， the total observation quantity is， necessary observations， and t necessary observations are selected as parameters. Each observation value is represented as a function of the selected parameter， and n error equations are listed. This adjustment method using the error equation as the function model is called indirect adjustment method. In the data processing of deformation monitoring and control networks， the indirect adjustment method based on the least squares principle can usually be used to adjust and analyze the point accuracy of the observed data in the network， calculate the mean square error of the weakest point， the mean square error of the weakest edge， and draw the error ellipse. The key to processing is the formulation of error equations， linearization of nonlinear conditional equations， solution of error equations， and accuracy evaluation of unknown points. This article takes the bridge control network deployed at Zijiang Third Bridge in Yiyang City as an example to derive the entire calculation process of the bridge control network and draw conclusions.

Keywords： Indirect adjustment;normal equation;Least squares principle;System of linear equations

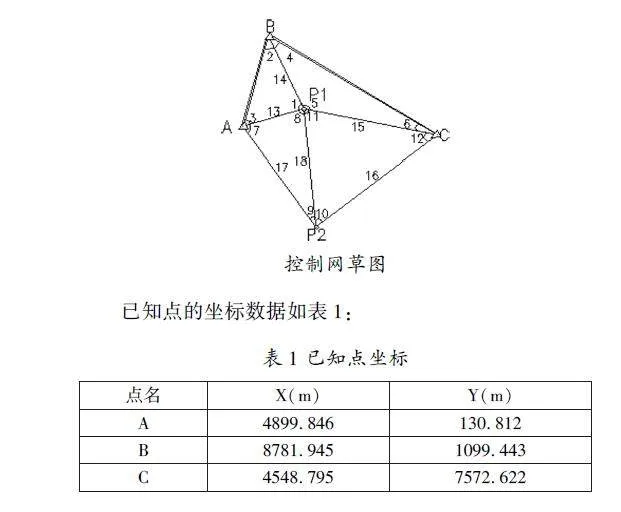
在现代桥梁控制网布设中，通常布设成GPS网或边角网[1]。布设为GPS网的优点是不受地形和通视条件的限制，布设为边角网的优点是既观测角度又观测距离，精度相对较高[2]。本课题结合边角网的布设优点对益阳市资江三桥进行控制测量。2021年以来，益阳市资江三桥由于车流量较大，投入使用时间较长，在运营过程中出现了桥墩倾斜下沉、桥面平整度发生变化的情况。为了了解资江三桥的真实变形速率及沉降规律，笔者布置了一测角测距的边角控制网。所用仪器为徕卡TC702型全站仪，测角中误差为±2″，测距精度为1mm+2ppm×D（公里）。如下图所示，A，B，C是已知点，P1，P2为待定点，网中观测了12个角度，2条边长（在条件平差中，不用观测边长；在间接平差中，用16，17作为观测边长）。，观测4个测回。控制网草图如下：

控制网略图

已知点的坐标数据如表1：

外业观测得到的数据如表2：

1间接平差解算

1.1间接方程的列立

n=14，t=4，r=10，u=4；可知要列立14个误差方程（已线性化）：

1.2间接平差的求解

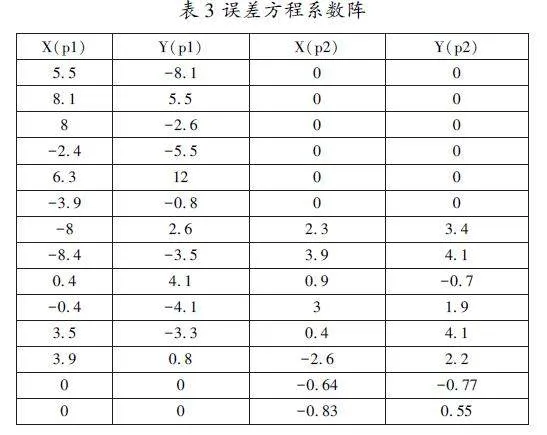
代入已知点数据，经过计算得到间接平差误差方程系数阵（如表3）：

间接平差中角度是等精度观测，测角中误差为2"，其中有12个角度观测值和2个边长观测值，则权阵为：

其中， ，以1Km观测为单位权观测值

常数项系数阵为：

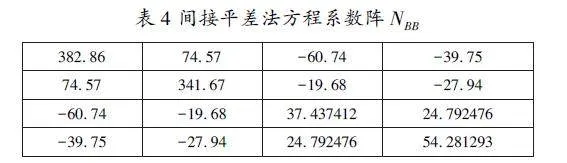
根据得到间接平差的法方程系数阵（如表4）：

根据得到：

，所以得到坐标改正数：

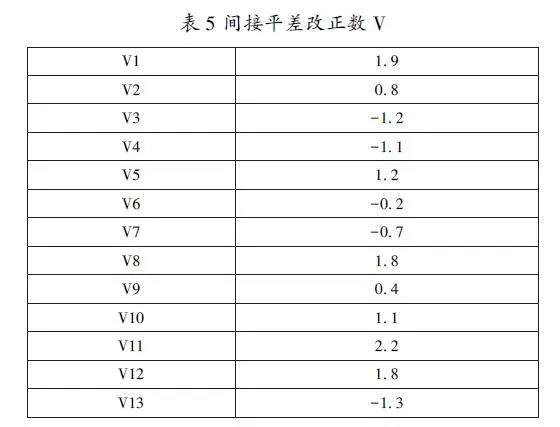
代入误差方程，得到改正数V（如表5）：

从而根据得到平差结果（如表6）：

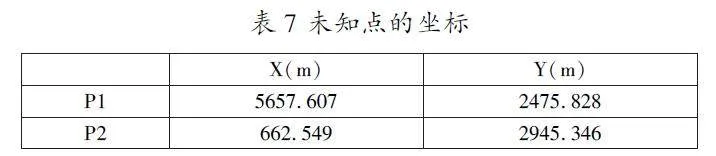
根据，得到未知点P1，P2的坐标（如表7）：

1.3间接平差精度评定

1.3.1单位权中误差

根据以上数据，可以得出：

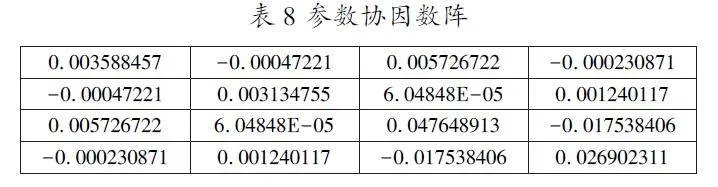
1.3.2参数向量的协因数阵（如表8）

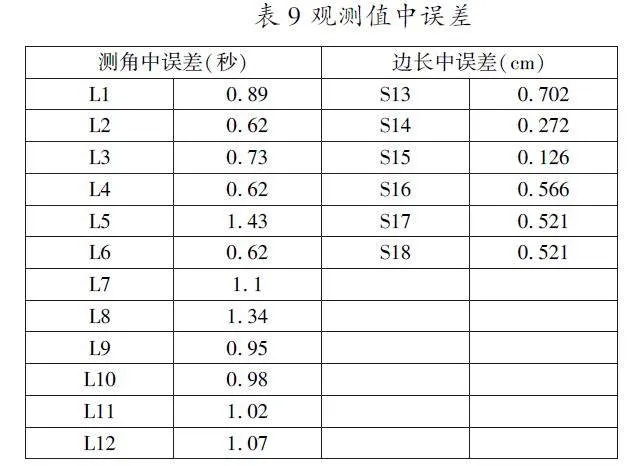
1.3.3观测值中误差列表（如表9）

1.3.4待定点点位中误差（如表10）

由可得未知数的权倒数：

P1，P2点的点位中误差：

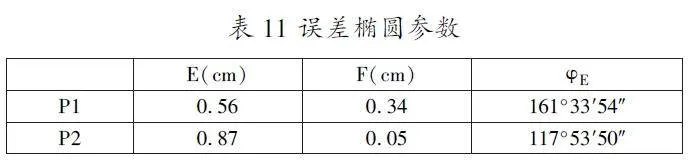
根据点位误差椭圆公式，可以得0c234ba2cfcad44b2b2cbd485eaff17f到P1，P2点的误差椭圆参数：

2条件平差与间接平差的比较分析

条件平差和间接平差都是具有无穷多组解的相容方程组。条件平差与间接平差都是在最小二乘准则的约束下求得最优解。对于同一平差问题，无论采用何种平差方法，所得到的平差结果和精度（包括点位中误差，点位误差椭圆）都是相同的。条件平差与间接平差是整个测量平差的基础，其他诸多平差方法都是在这两种平差方法的基础上发展起来的。

结语

条件平差和间接平差是整个测量平差的基础，其他诸如附有参数的条件平差和附有限制条件的间接平差都是在这两种平差方法的基础上发展起来的。在处理一般平差问题中，条件平差和间接平差可以比附有参加的条件平差和附有限制条件的间接平差更简易、直接的求出观测量的平差值。条件平差和间接平差所计算出的数据顺序是相反的，也就是说条件平差是先求出观测值的平差值，再通过公式求坐标值，而间接平差是直接求出坐标的参数值，再通过公式求出观测值的平差值。所以在工程实例中，间接平差比条件平差更直接，更具有优势，更容易被采用。

参考文献：

[1] 张正禄.工程测量学研究发展方向[J].现代测绘，2003，26（3）：3-6.

[2] 王晓光，谢振红.导线间接平差法[J].吉林建筑工程学院学报，2007，（01）：58-62.

[3] 张后苏.条件平差与间接平差间的转换[J].有色金属（矿山部分），1988，（04）：30-32.

[4] 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M].武汉： 武汉大学出版社，2003.

[5] 刘星，郭彩立，赵建云.现代测量平差理论的进展[C]//重庆市测绘学会.重庆市测绘学会第三届优秀论文评选获奖论文暨2005-2006年度学术交流会论文选编.重庆大学土木工程学院;，2008：7.

基金项目：湖南省自然科学基金联合基金项目（2022JJ50261）

作者简介：曹元志（1977— ）男， 汉族，河南信阳人， 硕士，副教授，注册测绘师，主要从事工程测量及数据处理的教学和科研。