超大跨连拱桥索力与施工线形计算分析

於勇

基金项目：广西重点研发计划“特大跨劲性骨架混凝土拱桥建造关键技术”（编号：桂科AB22036007）

作者简介：於 勇（1987—），工程师，主要从事道路与桥梁技术研究和施工管理工作。

为提高拱圈拼装精度和减少塔架施工变形，文章以在建某主跨为2×405 m的连续拱桥为工程依托，考虑扣索力和背索力对塔架变形和拱圈拼装变形的耦合关系，结合影响矩阵原理和最优化计算理论，建立多跨连续拱桥一次张拉施工计算方法。该方法应用于双跨连续钢管混凝土拱桥索力与施工线形计算中，使拱圈合龙线形较目标线形偏差控制在30 mm以内、塔架水平偏位控制在10 mm以内，各索力波动小，拱圈应力小、施工安全性好，具有良好的应用效果。

连续拱；塔上断开式扣索；斜拉扣挂；一次张拉；影响矩阵原理；线形

U448.22A321144

0 引言

根据文献［1］数据，现有钢管混凝土拱桥总数已有450余座，且多采用缆索吊运斜拉扣挂施工技术。近些年，随着拱肋跨径、吊重、吊装节段数量不断刷新纪录以及结构形式的多样化，钢管混凝土拱桥施工控制面临着新的挑战。

塔架作为缆索吊运斜拉扣挂施工的重要受力结构，根据扣索在塔上是否断开的情况，分为通长式扣索和塔上断开式扣索。塔上断开式扣索较通索相比，钢绞线无弯转，具有磨损少、受力更直接等优点，依托工程2×405 m连续跨钢管混凝土拱桥正是采用这种施工方式。拱桥斜拉扣挂施工索力和施工线形计算方法主要有零弯矩法［2］、零位移法［3-5］和优化法［6］等。这些方法各有优缺点，目前均鲜有应用于多跨连续拱桥的斜拉扣挂施工中，且对于分离式扣索布置也多以扣索力和背索力的水平方向力平衡的方式计算背索受力。由于施工过程中拱肋吊重不断发生变化导致施工过程中塔架变形较大，进而影响拱圈施工线形，导致施工过程中调索困难。

基于此，本研究结合影响矩阵原理考虑双连拱扣索力和背索力对塔架水平位移和拱圈竖向位移的耦合作用，再根据最优化计算理论，分别以拱圈悬拼过程中线形和合龙线形为优化目标和约束条件，建立一次张拉计算方法。最后，以在建某主跨2×405 m连续拱桥为工程依托，采用本文提出的计算方法进行拱桥扣索力、线形和拱圈应力等计算分析，为大桥的施工安全和施工质量保驾护航。

1 项目简介

1.1 设计概况

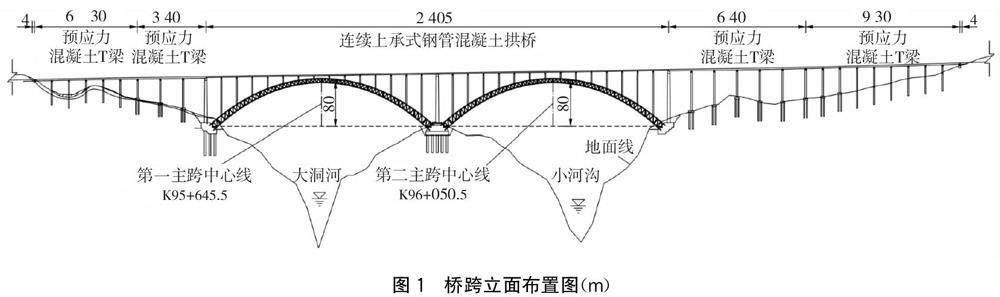
某特大桥采用两跨连续上承式钢管混凝土拱桥，单拱跨径均为405 m，矢高80 m，拱轴线为悬链线形式，拱轴系数为1.55。主拱圈采用两片拱肋以及中间横联拼装而成，单片拱肋为四肢桁式截面，弦管管径为1 400 mm，管内采用C70自密实混凝土灌注，桥面系主梁采用“开口钢板梁+混凝土桥面板”的钢混组合梁，单跨27 m，结构连续。根据地质情况的差异，两岸拱座分别为“扩大基础+桩基”和扩大基础形式，中间拱座采为“浅挖拱座+桩基础”结构形式。结构布置图如图1所示。

1.2 主拱圈

主拱肋为钢管混凝土变截面高度桁式结构，断面高度从拱顶的6.5 m变化至拱脚的11.0 m，单侧拱圈宽7.5 m，弦管管径为1 400 mm，上弦管拱脚至拱顶壁厚为分别为35 mm和32 mm，下弦管自拱脚至拱顶壁厚分别为35 mm、32 mm、28 mm，拱圈弦管采用Q390D钢材，腹杆、平联杆和横撑均为Q355钢材。弦管通过竖腹杆、斜腹杆和平联杆连接形成四肢矩形截面，两幅拱圈横向中心距17.5 m。

1.3 施工工艺

拱圈采用缆索吊运斜拉扣挂施工工艺，每跨单片拱肋均划分为18个拼装节段，最大节段重量为200.8 t，两肋间通过14道“米”字形横撑连接起来。如图2所示，缆索吊运系统采用355 m+99 m+300 m的跨径布置形式，中墩柱为“单塔双扣”施工，各扣索穿过墩柱内预留孔道锚固于墩柱表面。为保障施工安全和控制拱圈线形，两跨拱肋采用对称同步拼装施工工艺，先安装中墩两侧拱肋至合龙前段，再从两边墩分别拼装完成单片拱肋合龙，再安装肋间横撑。

2 斜拉扣挂仿真分析

2.1 有限元计算模型

采用Midas Civil软件建立该桥悬臂拼装分析模型，拱肋悬拼顺序按实际施工顺序仿真计算。大桥每跨单片拱肋均划分为18个拼装节段安装，全桥共划分为72个拼装节段。大桥有限元模型如图3所示。

2.2 斜拉扣挂计算方法

2.2.1 影响矩阵

施工过程中，两跨拱桥通过中间墩柱为媒介，线形相互影响，各塔架位移与拱圈位移也相互影响，可采用结合文献［7］的计算理论，考虑各因素之间的耦合作用。然而，文献［7］是仅对单跨拱桥进行施工分析，对于多跨连续拱桥斜拉扣挂施工需对其影响矩阵进行改进。

图4 两连拱斜拉扣挂布置示意图

如图4所示，各控制点的位移主要由恒荷载、背索、扣索以及其他荷载组成，结合影响矩阵原理［8-9］，可由式（1）方程表示：

式中：Cuser、Cconst、Cother[WB]——目标位移向量、恒载下位移向量和其他荷载下位移向量；

——各扣索和背索初拉力荷载向量；

——分别对单根索（扣索和背索）施加单位索力下各控制点的位移影响矩阵，故M和F分别如式（2）和式（3）所示：

式中：Δ1，2扣——2号扣索在单位荷载单独作用下对拱圈控制点1产生的竖向位移；

[KG8mm]1，2背——2号背索在单位荷载单独作用下对塔架控制点1产生的水平位移。

2.2.2 优化模型

根据最优化计算理论，分别以拱圈悬拼过程中线形和合龙线形为优化目标和约束条件，具体优化模型如下：

2.3 结果分析

2.3.1 拱圈应力

由图6可知，拱圈主弦管最大应力和最小应力分别为28.6 MPa和-83.2 MPa，发生在拱桥松索合龙的施工阶段，较Q420钢材具有较大安全富余。其余各杆件最大应力和最小应力分别控制在61.4 MPa和-65.6 MPa以内，最大应力始终发生在拱脚铰轴附近，较Q345钢材更有安全保障。

2.3.2 施工线形

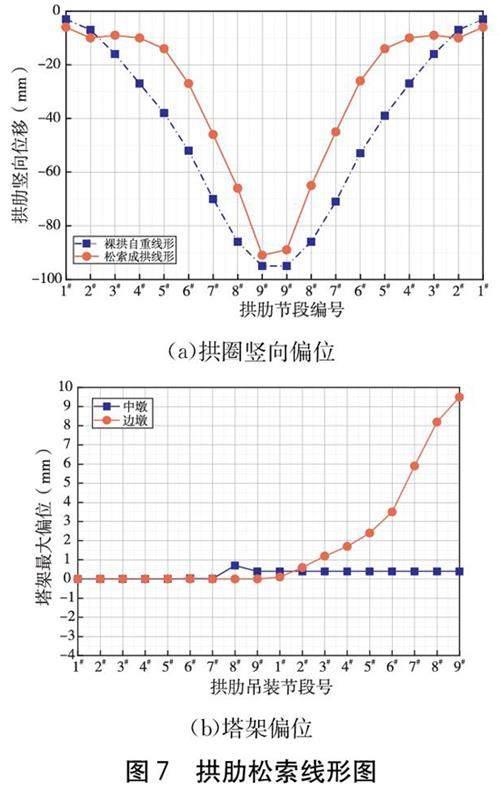
由图7可知，拱圈合龙松索后竖向变形与目标值偏差控制在＜30 mm，塔架水平位移＜10 mm，远小于规范规定的竖向偏位L/3000=135.0 mm和横向偏位L/400=211.3 mm［10］，表明了该桥拼装精度高，施工线形良好。

2.3.3 扣索索力

由图8和图9可知，在整个拱圈悬臂拼装施工过程中，各扣索索力变化值较小，其中，索力变化的最大值出现在4#扣索，索力变化量为202.0 kN，变化幅度＜23%；同一扣索在相邻两施工阶段中索力变化最大值为110 kN，索力变化幅度＜14%，索力均匀性较好。

采用本文方法进行某双跨连续拱桥的施工控制，实现了拱圈的高精度合龙。

3 结语

（1）通过考虑扣索力和背索力对塔架变形和拱圈拼装变形的耦合关系，基于影响矩阵原理和最优化计算理论建立的拱桥悬臂拼装索力和线形计算方法，有效克服了传统施工监控方法存在的塔架变形大、索力波动大、拱圈线形控制难等问题，显著提高了拱圈拼装质量和施工安全。

（2）从拱圈施工线形、索力和拱圈应力等方面对拱圈施工安全性进行分析，计算结果表明采用本方法进行拱圈斜拉扣挂施工控制，具有拱桥线形控制精度好、索力波动小、拱圈安全富余度高等优点。

（3）现有规范对拱圈松索合龙后的横向偏位和竖向偏位进行了规范要求，建议进一步对拱桥斜拉扣挂施工过程中线形和扣索力波动性提出规范要求。

参考文献

［1］Wang Q，Nakamura S，Chen K，et al.fatigue analysis of K-Joint in a half-through concrete-filled steel tubular truss arch bridges in china［C］. 8thInternational conference on arch bridges，2016.

［2］周水兴，江礼忠，曾 忠，等.拱桥节段施工斜拉扣挂索力仿真计算研究［J］.重庆交通大学学报，2000（3）：8-12.

［3］Kim K S，Lee H S.Analysis of target configurations under dead loads for cable-supported bridges［J］.Computers and Structures，2001，79（29/30）：2 681-2 692.

［4］胡大琳，陈定市，赵小由，等.大跨径钢筋混凝土拱桥悬臂浇筑施工控制［J］.交通运输工程学报，2016，16（1）：25-36.

［5］Lonetti P，Pascuzzo A.Optimum design analysis of hybrid cable-stayed suspension bridges［J］.Advances in Engineering Software，2014，73（5）：53-66.

［6］戴 杰，秦凤江，狄 谨，等.斜拉桥成桥索力优化方法研究综述［J］.中国公路学报，2019，32（5）：17-37.

［7］秦大燕，郑皆连，杜海龙，等.斜拉扣挂1次张拉扣索索力优化计算方法及应用［J］.中国铁道科学，2020，41 （6）：52-60.

［8］方 鸿，高 琼.影响矩阵法在系杆拱桥施工调索中的应用［J］.中外公路，2014，34（6）：146-148.

［9］杨 兴，张 敏，周水兴.影响矩阵法在斜拉桥二次调索中的应用［J］.重庆交通大学学报（自然科学版），2009，28（3）：508-511.

［10］GB 50923-2013，CFST拱桥结构技术规范［S］.