基于机器学习模型的节理岩体UCS预测方法
王海波 黄林冲 林越翔 马建军


摘要:节理岩体力学性能研判不明会对地下工程建设安全造成极大隐患,规范中对含节理岩体的力学性能判断多以粗略的定性分级为主,未给出明确的力学性能量化表征方法;而传统回归分析方法难以综合考量节理形貌多维度特性,岩体力学性能预判精度低。为探寻含节理岩体力学性质智慧量化预测方法,从含单节理岩体入手,广泛调研并收集了130组含单节理岩体单轴抗压强度(UCS),并采用节理倾角θ、节理贯通率k量化节理形貌特征,以弹性模量E及抗压强度σ表征岩石强度,开展基于机器学习的含单节理岩体力学性质智慧预测方法研究。为充分论证机器学习算法在岩体性能预测方面的适用性,引入神经网络、随机森林、支持向量机等多种机器学习算法,并采用分布统计、灰色关联分析等手段遴选关键控制指标,进一步结合k折交叉验证法训练映射网络,在此基础上比较了多种机器学习算法及传统回归分析模型的预测性能。研究结果表明:① 统计分析与灰色关联度分析可高效筛选指标组合;② k折交叉验证和多指标评价能有效减少机器学习模型的偶然误差;③ 整体上特征数量与预测效果成正比,其中支持向量机、随机森林分别为全参量预测和局部参量预测的最佳表现模型;④ 机器学习模型比经验、半经验得出的传统多元非线性回归模型预测效果更佳,充分展现了其在岩石力学性能智慧判别与预测中的巨大潜力。
关键词:节理岩体; 单轴抗压强度; 统计分析; 灰色关联分析; k折交叉验证; 机器学习
中图法分类号: U456.2
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2024.S1.040
0引 言
地下空间工程中常遇到由不规则节理、裂隙等结构组成的不连续介质体,即节理岩体。节理岩体中蕴含的节理结构是导致岩体稳定性下降的重要原因,严重影响隧道工程安全性,因此含不规则节理岩体强度一直是地下工程安全稳定性研究的重要课题[1-2]。宋英龙等[3]的试验研究表明,节理特性是节理岩体力学性能的重要影响因素,因此准确量化节理特征对节理岩体宏观力学性能的影响,对相关工程设计与建造至关重要。
受限于自然环境和岩体体积,节理岩石力学特性的相关实验难以通过原位试验完成,因此,目前现有的现场研究主要选择与天然岩体属性相似的类岩材料作为替代。例如陈超等[4]以云南红砂岩为研究对象,通过水泥、砂、硅灰以及树脂等制作了含不同节理倾角和贯通率的节理岩石试样,将类岩材料误差控制在10%以内,分析了节理倾角和贯通率对其单轴抗压强度(UCS)的影响;张波等[5]利用山东大学自主研发的新型类岩石相似材料-改性橡胶粉-水泥砂浆来模拟含交叉裂隙的岩石,通过多次单轴压缩实验明晰了裂隙角度变化对节理岩石的影响机制;刘浩[6]以砂岩为对象,结合正交试验实现了类岩材料的最佳配比,并针对节理倾角等特征开展单轴、三轴试验研究。此外,也有部分研究通过钻取天然岩石和裂纹切割制成含节理岩体试样,开展力学测试。例如,Liu等[7]用巴西劈裂法构建含不同形貌节理的岩体试样,分析其在单轴压缩下的力学特性;Jin[8]等以天然柱状玄武岩石为研究对象,对含有不同节理特征的岩石进行压缩试验,得出了节理对柱状玄武岩的影响机制。
综上,现有研究普遍认为节理几何形貌、空间位置对岩体力学性能影响显著,而岩石岩性则决定着岩体力学强度的根本基准。这两类特征共同影响并决定着含节理岩体的综合力学强度。为实现含节理岩体综合力学强度的量化评判,学者们采用回归分析等方法建立了一系列的力学预测模型。例如,杨科[9-10]等人用煤顶板岩石进行单轴压缩实验,分别建立线性函数、对数函数、多次函数等6种回归模型研究单轴抗压强度与弹性模量之间的关系。这类基于经验、半经验得出传统多元回归分析的力学强度预判,在预测精度及适用性方面依然存在显著局限。相比之下,基于机器学习的岩体力学强度预测,凭借其强大的信息捕捉能力和计算能力,能够准确描述高维变量之间的非线性关系,且具有极强的可移植性与普适性,近年来在岩土力学性能分析领域获得了广泛的关注与应用,并表现出了较好的性能[11]。
为突破传统手段对含节理岩石力学性能判断的局限,本文以单节理岩体为研究对象,从节理形貌与岩石物性入手,广泛调研并收集了130组包含节理倾角θ、节理贯通率k、完整岩样密度ρ、弹性模量E、抗压强度σ等多个参量的样本数据,开展基于机器学习的含单节理岩体力学性质智慧预测方法研究。为系统比较不同机器学习算法应用于含节理岩体力学性能预测的效果,本文引入了BP神经网络、随机森林、支持向量机等多种机器学习算法,并基于统计学与灰色关联分析量化遴选,构建输入参量组合,进而开展预测性能测试,以期为隧道及地下空间工程建设过程中的岩体性能量化及智慧估计提供技术参考与支撑。
1算法介绍
1.1BP神经网络
BP神经网络是典型的反馈神经网络,具有误差反向传播和动态权重更新的特点[12]。它基于生物神经系统的结构构建,包括输入层、隐藏层和输出层。输入信号经过不同的权重和阈值组合映射到下一层,并形成新的输入信号。通过激活函数处理后,输出结果单向传输到下一层,直到获得最终输出。
误差反向传播算法用于更新权重和阈值,利用梯度下降法计算每层误差相对于权重和阈值的梯度向量,并沿着梯度向量的反方向进行调整[13-14],直到输出结果达到预设精度或迭代次数。
1.2随机森林
随机森林算法是一种集成学习方法,旨在通过集体决策提高弱学习器的预测准确性[15]。它由回归树和随机集合组成。回归树包括根节点、中间节点和叶节点,将输入样本根据特征进行分类,最终输出对应的结果。
此算法的核心问题是选择最佳特征分割点和输出值,可使用二进制方法来多次确定。随机森林通过特征和样本的随机化过程,保证了树之间的部分相似性,从而减少欠拟合和过拟合,并提高集体决策的可靠性。
1.3支持向量机回归
支持向量机回归(SVR)是一种有监督的学习算法,通过优化结构和减小风险来提高模型的泛化能力,实现经验风险和置信范围的最小化[16]。与传统线性回归相比,SVR的计算方式有所不同。它在回归线周围设定阈值,形成一个区域,如图1所示。通过将区域内样本点误差定义为0,并计算区域外的损失,将回归问题转化为最优化函数问题[17]。具体的简化和求解过程不再赘述,最优化目标函数如公式(1)所示:
minw,b=12‖W‖2+Cni=1lεfxi,yis.t.0≤yiwTxi+b≤1(1)
式中:w为超平面的n维法向量,决定超平面的方向;b为偏置项,代表超平面到坐标原点的距离;C为惩罚变量,l为损失函数。为了更容易得出回归方程,通过引入核函数,将低维样本空间映射到高维特征空间用以更快速地寻找超平面[18],如图1所示。
对于样本容量为n的问题,计算维度往往是n2,n3或者更高,显然,在面对小样本范围和不简单的数据时,支持向量机回归模型往往可以兼顾计算精度和计算效率。
2样本数据
2.1数据源
本文使用的数据集来源于已发表的各类学术论文,以核心期刊论文和学位论文为主。根据目前各类已有的实验研究数据情况[19-21],诸多因素都对含单节理岩石的单轴抗压强度有显著影响,且面对不同的对象影响程度有所差异。数据库中所有输入及输出参数的直方图以及变量之间的散点如图2所示。为了有效验证和分析各变量对UCS的影响程度,本文收集的数据集主要囊括岩石节理特征(JRC、倾角、贯通率等)和完整岩石特性(密度、泊松比、弹性模量等)两部分。经过筛选和整理后,最终选取了一个关键输出指标,即单轴抗压强度(UCS);5个关键输入参数,分别为节理倾角θ、节理贯通率k、完整岩样的密度ρ、弹性模量E、抗压强度σ,一共130组数据。由图2可知:岩石节理特征相互独立,且与岩石岩性关系极不显著,而表征岩性的各指标之间相关性显著。故据此可将节理特征可视为独立变量,并遴选岩性参数指标,研究在不同特征输入参数组合下,对岩体力学性能的预测效果。
2.2灰色关联分析
灰色关联分析(grey relation analysis)在工程领域被广泛用于评估因素之间的同步变化程度[22-23]。为消除不同量级对模型的影响,提高计算效率,首先对全特征的样本数据进行标准化处理,将其转化为无量纲的数据,标准化公式如下:
xnorm=x′-xminxmax-xmin(2)
式中:xnorm为标准化计算结果,x′为特征序列中任意值,xmax和xmin分别为特征序列里的最大值和最小值。基于上述标准化数据构建关联矩阵,然后计算各个因素与参考项之间的关联度,计算公式如下:
G(xr(j),xi(j))=miniminjxr(j)-xi(j)+δmaximaxjxr(j)-xi(j)xr(j)-xi(j)+δmaximaxjxr(j)-xi(j)(3)
式中:G(xr(j),xi(j))代表第i个特征和参考特征序列中第j个数据之间的灰色相关系数,δ为取值范围(0,1)之间的调节系数。任意两个特征序列之间的灰色相关系数计算公式如下:
G(xr,xi)=1nnj=1G(xr(j),xi(j))(4)
计算结果如图3所示。
结合数据分布规律直方图和灰色关联分析热图3结果可见,随机变量之间的可作定量描述,由于节理特征在实验中的赋值完全取决于研究人员,主观性较强,因此在节理特征部分可能存在规律性较强的协同变化,这在图3中也有体现,例如节理倾角和节理贯通率的相关系数偏大、节理的贯通率和弹性模量的关联性偏小等。因此,在此条件下的节理特征之间、节理特征和岩样特征之间的关联数据参考程度不强,所以在考虑特征分组依据时,应重点关注单变量特征与因变量结果之间的关联程度,同时,为研究不同参量以及不同参量数量对自变量的影响,对组内自变量与因变量的灰色关联系数取平均值,结果见表1。
根据表1,本文分别遴选了平均值较大的4种不同的特征参数组合,即:θ-k-ρ-E-σ、θ-k-ρ-E、θ-k-ρ-σ、θ-k-ρ,开展基于机器学习的岩体力学性能强度预测实验。
3实验模型
3.1k折交叉验证
本文使用的数据集来源于多个不同研究实验,为减小实验误差,提高机器学习模型的的性能和泛化能力,通过k折交叉验证方法[24](本次实验取k=5),将原始数据集随机分成5个大小相等的子交叉验证集,其中4个子交叉验证集用于模型训练,剩下的1个子交叉验证集用于模型测试。将上述过程重复5次,最终会得到5个独立的模型性能评估结果。k折交叉验证可以更准确地评估机器学习模型在未知数据上的表现,实现对模型性能的可信度评估。
3.2模型框架
图4展示了本文建立节理岩石的单轴抗压强度(UCS)的预测模型构建流程图。主要分为4个阶段:数据预处理、k折交叉验证、训练和测试以及结果分析评价过程。
数据预处理工作包括收集因变量UCS及主要影响因素的数据集,建立输入和输出参数数据库,开展灰色关联分析,初步确立各变量的相关程度,并且以此为根据对特征进行划分得到多个特征集。第二阶段通过k折交叉验证方法将上述每一个特征集等量划分成80%的训练集和20%的测试集进行交叉验证,训练和测试阶段用到了多个预测模型,将上述划分后的训练集和测试集编号并作为输入,最后输出每个模型的结果进行比较,进一步评价各模型的适用范围。
4实验结果分析
输入变量的选择对模型的性能至关重要,根据灰色关联程度分析,独立的特征变量对节理岩石单轴抗压强度影响程度各不相同,结合节理特征对于节理岩体单轴抗压强度影响的研究方向,因此本次实验分别选择全特征组和局部特征组合。
4.1评价指标
本文选用均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)3个常用指标来评估机器学习模型的性能[25]。3个指标各有优劣,可用来对同一个样本做对比评价。RMSE和MAE直接反映了预测误差,且对异常值敏感,尤其是RMSE的平方项对于离群点给予了更多的惩罚。
即使少量异常值也可能导致RMSE值偏大,相比之下,MAPE是一个与样本尺度无关的指标,百分比误差消除了数据单位影响,MAPE的不足之处在于绝对值项使得其对正误差惩罚更小,同时输出值y趋近于0时,MAPE趋于无穷大。综上所述,评价指标各有优劣,RMSE、MAE和MAPE的组合可以有效地评估模型性能,3个指标的表达式如下:
RMSE=ni=1y-yi2n(5)
MAE=1nni=1y-yi(6)
MAPE=1nni=1y-yiy(7)
4.2模型评价
主要的超参数设置如表2所列,本次实验选用了3种复杂程度和超参数数量接近,并且选择具有代表性的机器学习模型进行试验。
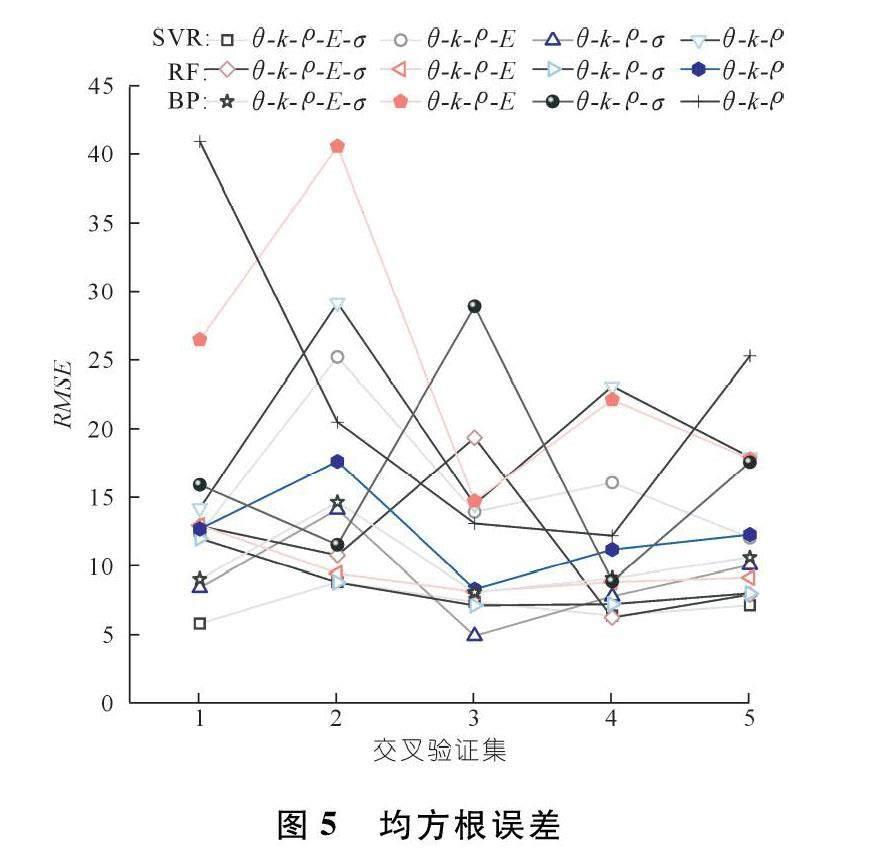
图5~7展示了算法模型-特征组-交叉验证的共计60次测试结果。从图中折线的变化趋势可知,不同交叉验证集的结果之间存在明显的差异,例如基于第二验证集的实验误差均存在偏大现象,对比单次随机抽样方法,k折交叉验证方法能够更为全面地展示数据集的特点,同时极大程度规避了单次试验诱发的偶然误差影响,提高了对预测精度评判的客观性。
图5和图6除了在具体数值上存在差异以外,二者整体的变化规律趋于一致,结合公式(5)和公式(6)的函数性质,不难解释二者变化相似的特点。值得注意的是,部分数据点表现在这两幅图中相反,如第4次交叉验证实验中,SVR模型测试的θ,k,ρ特征组和BP神经网络模型测试的θ,k,ρ,E特征组等,再次暴露了单一模型和单次实验存在的局限性,极容易产生错误甚至完全相反的评价结果。
因此,需要对实验结果进行多维度的评价分析,通过综合多参数评价结果判定模型预测性能,结果如表3所列。
对于任意模型,误差之和越小,模型预测准确率越高。由表中数据可知,通过支持向量回归模型测试的全特征样本实现了最小平均误差,BP神经网络模型测试的θ,k,ρ,E特征组预测效果最差。特征组包含特征参数越多,输入参数与输出参数之间的映射关系重构越充分,预测效果越好。四变量参数组合中,θ,k,ρ,σ特征组的预测效果最优。
对于机器学习模型来说,虽然随机森林模型未达到最佳的预测性能,但是对每组特征样本的测试,其结果都表现出较为稳定的误差控制,模型平均误差最小。尤其是在输入参数较少的情况下,随机森林模型的误差稳定,表现出了优异的泛化能力。此外,随机森林模型的预测结果最接近于灰色关联分析结果。因此,随机森林模型可以认为是本次测试实验的最佳模型。
4.3与经验、半经验模型比较
文献[24-25]利用SPSS软件结合多种类型函数和实验数据,尝试构建节理岩石强度的经验模型。结果表明经验、半经验模型在预测精度方面存在一定的局限性。为了进一步验证机器学习模型的性能,随机选择一个测试样本,对于相同的训练集,利用SPSS软件拟合多元非线性函数,表达式如下:
y=0.029x1-20.788x2+5.449x3+0.055x4+
0.535x5+0.05x1-1.48+2.1x247.829+
1.66e-9.926(x3+x4)x5-1.358
(8)
将上述公式测试结果与机器学习模型拟合结果进行比较,结果如图8所示。
由图8可知,机器学习模型之间的预测表现各不相同,但是其结果均优于传统的多元非线性模型,可见机器学习模型具备独特的自动提取变量特性和强大的建模能力,而传统分析模型仅针对类似问题可给出良好的解决方案,在处理映射关系更复杂的样本时,准确性会明显下降。
5结 论
本文以地下空间建设过程中常见节理岩体为对象,对其抗压特性的研究现状进行了系统调研,整理收集了包含节理特征和岩样特征的现场实验数据,并且对这些数据进行了分布统计分析和灰色关联分析的预处理工作,对特征进行了划分。然后结合支持向量回归、随机森林和BP神经网络3种机器学习模型对划分的特征组样本分析和预测,并且与经验、半经验模型进行比较。主要结论有:
(1) 联合统计分析与灰色关联度分析可高效量化指标组合,有效筛选得到具有代表性的关键控制指标组合。
(2) k折交叉验证有效提高了模型泛化能力,避免了样本特性导致的实验误差,多误差综合评价从多个维度科学地减小机器学习模型预测的偶然误差,确保对模型性能得出准确、客观评价。
(3) 整体上,输入参量越多,含节理岩体性能预测效果越好;在采用全参量预测时,支持向量机算法得到的预测结果误差最小,而在采用局部参量进行预测时,随机森林算法的泛化能力最强,预测精度最为稳定,反观支持向量机算法及人工神经网络算法误差均出现了明显的增长。
(4) 相较于经验、半经验推导出的简单多元非线性回归模型,机器学习模型通过不断学习和更新,在适应性、泛化能力、预测能力、可解释性方面均体现了更好的效果,充分展现了机器学习算法在岩石力学性能智慧判别与预测的巨大潜力。
参考文献:
[1]杨明明.高应力下不同节理倾角的隧道稳定性影响研究[J].武汉交通职业学院学报,2022,24(4):130-135.
[2]赵金锐.层状节理对深埋隧洞岩爆的影响[D].西安:西安理工大学,2022.
[3]宋英龙,夏才初,唐志成,等.不同接触状态下粗糙节理剪切强度性质的颗粒流数值模拟和试验验证[J].岩石力学与工程学报,2013,32(10):2028-2035.
[4]陈超,王伟,许高杰,等.考虑不同节理倾角和贯通率的类岩材料单轴压缩试验[J].河海大学学报(自然科学版),2022,50(5):124-130,146.
[5]张波,李术才,杨学英,等.含交叉裂隙节理岩体单轴压缩破坏机制研究[J].岩土力学,2014,35(7):1863-1870.
[6]刘浩.类砂岩材料单节理岩体卸荷力学特性研究[D].北京:北京交通大学,2020.
[7]LIU X G,ZHU W C,ZHANG P H,et al.Failure in rock with intersecting rough joints under uniaxial compression[J].International Journal of Rock Mechanics and Mining Sciences,2021,146:104832.
[8]JIN C,LI S,LIU J.Anisotropic mechanical behaviors of columnar jointed basalt under compression[J].Bulletin of Engineering Geology and the Environment,2018,77(1):317-330.
[9]杨科,袁亮,祁连光,等.淮南矿区11-2煤顶板岩石单轴抗压强度预测模型构建[J].岩石力学与工程学报,2013,32(10):1991-1998.
[10]ALADEJARE A E.Evaluation of empirical estimation of uniaxial compressive strength of rock using mea-surements from index and physical tests[J].Journal of Rock Mechanics and Geotechnical Engineering,2020,12(2):256-268.
[11]李磊,陈向东,丁星,等.基于图像处理与机器学习的岩土湿度检测系统[J].传感器与微系统,2020,39(6):83-85,88.
[12]WANG Z H,CHEN Q Q,WANG Z Y,et al.The investigation into the failure criteria of concrete based on the BP neural network[J].Engineering Fracture Mechanics,2022,275:108835.
[13]任建平,宋仁国,陈小明,等.基于BP神经网络梯度下降算法的7003铝合金热处理工艺优化[J].宇航材料工艺,2009,39(4):6-9,57.
[14]CHENG Z L,ZHOU W H,GARG A.Genetic programming model for estimating soil suction in shallow soil layers in the vicinity of a tree[J].Engineering Geoology,2020,268:105506.
[15]GAL Y,GHAHRAMANI Z.Dropout as a Bayesian approximation:representing model uncertainty in deep learning[C]∥International Conference on Machine Learning,2016.
[16]DANIEL V C,JAVIER A,MERCEDES L.Comparing two SVM models through different metrics based on the confusion matrix[J].Computers & Operations Research,2023,152:0305-0548.
[17]LUIS C P,MARTN C,ALFONSO R D,et al.A novel formulation of orthogonal polynomial kernel functions for SVM classifiers:The Gegenbauer family[J].Pattern Recognition,2018,84:211-215.
[18]王旭.不同倾斜角度及贯通度节理类岩石力学和蠕变特性研究[D].淮南:安徽理工大学,2021.
[19]汪中林.单轴压缩下单裂隙类岩石力学特性和破坏规律研究[D].荆州:长江大学,2018.
[20]田威,余宸,王肖辉,等.3D打印裂隙岩体动态力学性能及能量耗散规律初探[J].岩石力学与工程学报,2022,41(3):446-456.
[21]麦加里.实用软件度量[M].北京:机械工业出版社,2003.
[22]张涛,平西建.基于差分直方图实现LSB信息伪装的可靠检测[J].软件学报,2004,15(1):151-159.
[23]万俊杰,任丽佳,单鸿涛,等.基于灰色关联分析与ISSA-LSSVM的配电网可靠性预测[J].控制工程,2023,30(5):856-864.
[24]STONE M.Cross-validatory choice and assessment of statistical predictions[J].Journal of the Royal Statistical Society,Series B(Methodological),1974,36(2):119-132.
[25]HYNDMAN R J,KOEHLE A B.Another look at measures of forecast accuracy[J].International Journal of Forecasting,2006,22(4):679-688.
(编辑:郑 毅)

