运用变式教学优化学生数学认知结构的策略研究

胡亨

摘  要：当下的中学数学教学常常出现教师的教与学生的学无法很好对应的现象，而这种不对应很大程度上源自教师与学生的数学认知结构之间的差异。学生想要在数学学习上达成较高的成就，往往需要构建起一个良好的数学认知结构，因此，寻找合适的教学途径优化学生数学认知结构成为数学教师亟须攻克的一大难题。变式教学作为我国数学教育中一种常见的教学方式，对学生发现问题本源并主动构建相应知识体系有很大的帮助。文章将重点分析运用变式教学优化中学生数学认知结构的可行性，并在此基础上总结优化中学生数学认知结构的有效策略，以供参考。

关键词：数学变式;数学认知结构;动点问题

中学生的数学认知结构水平具有较大差异性，主要体现在学生数学知识的广度、学生认知的层次性和逻辑性等方面。当前越来越多的数学教师尝试运用数学变式教学推动学生从问题本源出发，优化认知结构。本研究从数学变式与数学认知结构的特点入手，解析两者的内在关联，并以“线段上的动点问题”变式教学为例，分析运用变式教学优化学生数学认知结构的有效策略，希望能有助于提升学生的数学学习效果。

一、数学认知结构和变式教学概述

（一）数学认知结构的概念和特点

数学教育专家曹才翰先生对数学认知结构界定为学生头脑里的数学知识按照自己的理解深度、广度，结合自己的感觉、知觉、记忆、思维、联想等认知特点，组合成的一个具有内部规律的整体结构。从数学认知结构的概念出发，可以发现学生的数学认知结构有着几个重要的特点。一是个体性，数学认知结构和学生心理发展水平是相辅相成的，学生的心理结构会影响其内化数学知识的组成方式，正是由于每个人的心理水平不一样，数学认知结构在学生之间存在显著的个体差异;二是结构性：学生大脑中的数学认知结构是成板块结构的，新知识内化到学习者的大脑中，学生再将知识进行自我划分和规划，形成知识之间主体与分支、内涵和外延的结构化体系。

（二）变式教学的概念和特点

上海市教育科学研究院的顾泠沅先生把变式教学分为两种：概念性变式和过程性变式。他把概念性变式定义为“在教学中用不同形式的直观材料或事例说明事物的本质属性，或变换同类事物的非本质特征以突出事物的本质特征，目的在于使学生准确掌握概念，区分和理解事物的本质特征和非本质特征”;同时把过程性变式定义为“通过有层次的推进，使学生分步解决问题，积累多种活动经验，是一个关注学生动态的、内在的、层次性递进的过程”。

结合教学实践经验，可以发现变式教学有两个非常显著的特点：开放性和本源性。开放性体现在变式教学提供问题的主体部分，而把问题的变化方向交给学生和教师，学生可以依据自己的认知结构对问题的概念、条件、所求进行适当变形。本源性是变式教学最为核心的部分，任何的“变”都是基于“本”的基础，问题本源就像是大树的树干，而多样的变式则是树枝，任何树枝的生长都离不开树干的滋养，如果变式脱离了本源，那么最终结果就会导致学生数学认知结构的错乱。

（三）数学认知结构和变式教学的联系

从数学认知结构和变式教学的特点上看，两者存在一定的对应关系。数学认知结构具有个体性，而变式教学固有的开放性可以满足学生个体性需求，基于每个学生的现有知识结构进行合理变式，有利于教师了解学生的现有认知结构水平，并从学生的已知经验出发引导学生进行合理变式;数学认知结构还具有结构性，学生对知识结构存在一定的理解，但可能这种理解存在偏差，变式教学的本源性正好可以帮助学生厘清知识脉络，找到知识主体，并且从问题本源出发，梳理知识点的分支，构建一个更为详细而庞大的知识体系。

（四）运用变式教学优化中学生数学认知结构的可行性

何小亚认为，良好的数学认知结构包括以下四个特征：足够多的观念、稳定而又灵活的产生式、层次分明的观念网络结构、稳定的问题解决策略的观念。那么变式教学能否帮助学生达到这四个特征呢？答案是肯定的。

一方面，在变式教学中，生生之间的信息交互可以促进学生的信息共享和灵感迸发;另一方面，变式教学能帮助学生认清问题本源，理解题目演变的技巧和方法，对整个知识点的架构有更加清晰和充分的了解。而最终通过归纳通用的解题策略，可以帮助学生形成多题一解的观念，引导学生找到有效解决一类问题的有效策略。下文将以“线段上的动点问题”为例进行变式教学的阐述，分析优化中学生数学认知结构的策略。

二、课例阐述——线段上的动点问题

本研究选取浙教版七年级上册数学教材第六章“图形的初步知识”中有关线段长短比较以及线段和差的拓展知识“线段上的动点问题”进行变式教学。

原题：A、B两城市相距16千米，小林骑车以每小时3千米的速度从A市出发前往B市，小明同时步行以每小时1千米的速度从B市出发前往A市。问多少时间后小林和小明相遇？

本题意在引导学生从实际情境中抽象出数学模型“线段上的动点模型”，经由C点表示小林，D点表示小明，运用数形结合思想分析问题解决策略（见图1）。在解决这道问题时，教师应引导学生尽量尝试用代数式表示线段长度的方法，把时间设为t，则线段AC=3t，线段BD=t，分析两人相遇时C、D点的位置关系，运用方程思想发现AC+BD=16解决问题，为后续寻找变式通用解法提供帮助。

变式方向1：改变已知条件。

变式①：小明步行速度改为每小时2千米，问何时相遇？

变式②：小明步行速度不变，比小林提前一个小时从B市出发前往A市，问何时相遇？

变式方向2：改变提问。

变式③：问小林到达B市时，小明距离A市还有多远？

变式④：问何时小明和小林两人相距2千米？

变式方向3：增加外延。

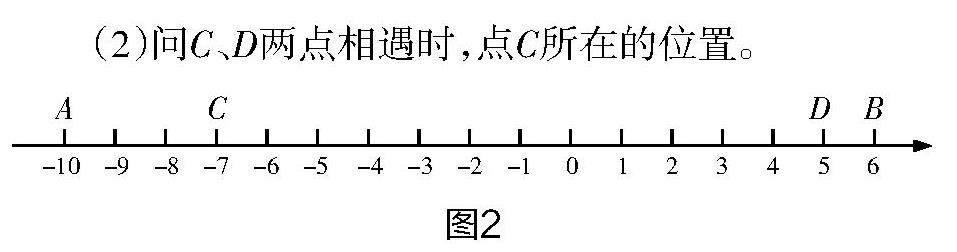
变式⑤：已知A、B两点在同一数轴上，点A在原点的左侧，与原点相距10个单位，点B在A点的右侧且两点相距16个单位长度。点C以每秒3个单位的速度从点A出发在A、B两点之间来回运动，点D以每秒1个单位的速度从点B向点A运动（见图2）。

（1）求点A、B所表示的数。

（2）问C、D两点相遇时，点C所在的位置。

[A                    C                                                                                          D     B][-10    -9  -8  -7  -6  -5      -4  -3  -2  -1       0        1   2        3        4        5   6]

图2

变式⑥（改变已知条件）：若D同时以每秒1个单位的速度从点B出发，在A、B两点之间来回运动，求C、D两点第四次相遇时，相遇点所表示的数为多少？

变式⑦（改变提问）：在变式⑥的基础上问第100次相遇点所表示的数为多少？

上述实例中采用了三种变式方向：改变已知条件、改变提问、增加外延。其中变式①和变式②对已知条件进行一定的修改，编题和解题难度都不大，完全可以由学生自主产生，以帮助学生巩固本源问题的基本解决策略，数学认知结构发展薄弱的学生也可以获得完成的成就感，巩固了学生对本源问题主体部分的认识。变式③和变式④对提问方式进行了改变，帮助学生不断拓宽数学认知结构，基于主体部分所展开。教师可以提问：“你还能求出哪些情况？”引导学生开放探究。其中变式④对学生的思维提出了较高要求，运用方程思想需要学生能综合运用线段和差的有关知识，并且还需要认清“相距2千米”包含两种情况，一种是C点在D点的左侧，另一种是C点在D点的右侧。此时，教师应着重引导学生从题目出发联系生活实际，帮助学生真实体会分类讨论思想的必要性。变式教学中具有较高变式难度的是通过联系多个知识点来扩充更大范围的数学认知结构，往往会在编题、解题和理解上都对学生提出更高的要求。变式⑤在线段上的动点问题的基础上，通过引入数轴这个概念，进一步完善和拓宽学生有关“线段上的动点问题”的数学认知结构。第二小问有关相遇点的探究既是对变式②的再拓展，把线段关系和数轴上点的位置关系相联系，更考查了学生的分类讨论思想，即C点在A、B两点之间来回运动过程中与D点多次相遇，而C点每次改变运动方向后，有关线段长度与运动时间的代数式均会发生改变，依据点的运动路程和点的运动轨迹正确表示对应线段长度是这个问题的难点，对学生的逻辑思维和运动分析能力提出了较高要求，能够实现学生深度思维的开发。变式⑥是对变式⑤中问题解决策略的再次应用和巩固，而变式⑦是基于变式⑤和变式⑥帮助学生寻找核心数学规律，有助于学生对数学方法的类比和归纳，由特殊的运动条件转化为对一般的规律性问题的思考，具有更高的思维要求，让部分学有余力的学生深度挖掘思维逻辑，拓展数学认知结构。

三、运用变式教学优化学生数学认知结构的有效策略

（一）确定先行组织经验，创设丰富变式结构

要想构建良好的数学认知结构，必须熟悉学生原有的数学认知结构。奥苏贝尔的同化理论强调，有意义的学习需要教师先认清学生的先行组织者，从而把握教学起点进行有针对性的教学，以便将数学新知识同化到学生原有数学认知结构中去。变式教学同样基于学生的原有认知结构开展，需要教师在认清学生先行组织者经验的前提下尽可能多地设想学生可能性的提问，创设丰富的变式结构，在改变条件、改变提问、增加外延等方面下足功夫，在本源问题的主导下进行合理解答和变式，不能盲目变式，忽略学生的理解和接受情况，脱离学生实际认知的变式就是失败的变式。

（二）创设良好问题情境，引导学生自主变式

良好的问题情境可以帮助学生从生活实际出发快速理解问题本源的内涵和本质，引发学生自主和合理的逻辑探究与策略归纳。但是介于学生的个体差异，以及变式教学的开放性，在整个教学过程中不能“放任自由”，需要教师作为主持人进行合适的引导，帮助学生正确构建“基于主体的分支变式”。这既是优化教学效率的必要手段，又是帮助学生正确构建问题体系的必要手段。这对教师提出了较高的要求，需要在教学设计环节投入更大的心血，对每个设想的情境与问题都要组织好过渡语言，用恰到好处的指点进行引导。

（三）围绕问题本源拓展，抓紧核心解题策略

良好的变式教学必须紧紧围绕问题本源，从知识主体的通用解决思路、策略出发构建知识网络。变式教学只有紧紧依托于合理的知识网络才能起到完善学生数学认知结构的要求。教师要想通过变式教学搭建合理的知识网络，首先自己必须理清知识的内在逻辑，这就要求教师对教材有更为深刻的理解和认识，能发现数学知识点之间的逻辑关系和合理演变。其次，变式教学尤其注重核心解题策略的归纳与应用，所有的变式围绕本源。核心解题策略必须在教学起始就点明，并在后续变式中不断深化与强化，以帮助所有学生掌握、理解并运用好策略解决问题。

（四）强调数学思维归纳，提升数学思想认知

学生的成长轨迹以及基于长期实践的理论研究都表明，形成数学思维在培养学生的数学素质方面有重要作用。数学思维具有高度的概括性和迁移性，在数学认知结构的建构和优化过程中，应当突出数学思维方法的归纳，帮助学生构建思想层面的数学认知。例如本文课例中牵涉解决“线段上的动点问题”的基本思路是方程思想的运用，而在题目的变式中又牵涉了分类讨论思想，这些重要数学思维的归纳对学生把握这一类问题的解决策略都有很重要的指导作用，对学生数学认知结构的完整化起着至关重要的作用。

四、结语

本研究从数学变式和数学认知结构的特点出发分析了运用变式教学优化中学生数学认知结构的可行性，结合实例分析了如何运用变式教学优化中学生的数学认知结构，最后提出了四条对应的运用策略。变式教学是数学教育教学中具有特色的一种教学模式，改善和精进变式教学策略可以很好地提升数学教学的效果，也是当下值得广大数学教师研究的一个重要课题。

参考文献：

[1]张程，张景斌. 中学生数学知识建构水平差异性的实验研究[J]. 数学教育学报，2004（02）：49-51.

[2]张亚鲜. 初中生数学认知结构的调查分析与建构策略研究[D]. 新乡：河南师范大学，2016.

[3]顾泠沅，杨玉东. 过程性变式与数学课例研究[J]. 上海中学数学，2007（Z1）：98+1-5.

（责任编辑：廖  艺）