考虑土拱效应的多层土体墙后主动土压力模式研究

李文彪 吕延豪 游龙飞

收稿日期：2023-05-06；接受日期：2023-06-23

基金项目：中铁第四勘察设计院集团有限公司科技研究开发计划项目（2021K027）

作者简介：李文彪，男，高级工程师，主要从事超深风井开挖及稳定性方面的研究。E-mail：004523@crfsdi.com

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2024） 06-0204-07

引用本文：李文彪，吕延豪，游龙飞.考虑土拱效应的多层土体墙后主动土压力模式研究

［J］.人民长江，2024，55（6）：204-210.

摘要：土拱效应已经被广泛证明存在于岩土工程中，然而关于土拱效应的土压力研究目前常局限于单层土体，对于多层土体墙后主动土压力的分布规律尚不清楚。基于土拱效应理论，提出了多层土体挡土墙后非线性主动土压力求解公式，并通过两种典型地层研究了土体内摩擦角和墙土摩擦角对主动土压力分布规律的影响。结果表明：所提出的计算公式能够很好地描述多层土体墙后主动土压力分布规律，计算结果与数值模拟结果基本一致；当上、下土层参数一致时，该公式可以退化成单一土层土压力计算模型；当墙土摩擦角充分发挥时，上层土体墙后土压力受土体内摩擦角影响明显，而当墙土摩擦角部分发挥时，下层土体墙后土压力受墙土摩擦角影响更大。

关  键  词：土拱效应； 挡土墙； 多层土体； 主动土压力

中图法分类号： TU432

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.06.028

0  引 言

挡土墙的墙后主动土压力一直是岩土工程学科中的重要研究课题。目前，经典土压力理论解和基于有限差分和有限元法等的数值手段是墙后土压力求解过程中常常采用的两类典型方法。其中经典土压力理论基于朗肯土压力［1-2］和库伦土压力［3-4］。朗肯土压力理论假定墙后为竖直光滑，库伦土压力在朗肯土压力理论的基础上做了改进，拓展到了墙后倾斜且有墙土摩擦角的一般情况。然而经典土压力理论解的局限性在于墙后土体的土压力分布为线性增加的分布模式，这与大量室内试验以及实际监测结果相悖，墙后土体往往是一种非线性的分布模式［5］。

土拱效应广泛存在于岩土工程中，如桩承式复合路基、地下管道、抗滑桩［6］、盾构等结构的应力集中和扩散现象。Terzaghi［7-9］最早研究了土拱效应，并对土拱效应进行如下定义：“当土体受到不均匀变形时，变形较大区域和变形较小区域存在一种剪切摩擦力，这种剪切摩擦力有阻挠变形较大区域土体继续运动的趋势和增加临近静止区域土体变形的趋势”。由此可知，土拱效应实际是一种应力重分布的现象。Finn［10］采用弹性理论研究了土拱效应，然而这种理论仅当土体处于小变形时才有效。实际情况是土拱形成时往往伴随着大变形，所以应用塑性理论特别是极限分析方法比较合适。Wang等［11］在边坡工程的抗滑桩设计时应用了土拱效应，把边坡假设成一个经典无限边坡模型，滑面上土体假设成理想刚塑性，滑面下卧非常坚硬的基础。他们得到如下结论：土拱效应存在于黏性土和无黏性土边坡中，存在一个极限桩间距，当桩间距超过这个极限值时，土拱效应消失。土拱效应影响因素颇多，c、φ值对土拱效应影响最明显。应宏伟等［12］基于传统的考虑土拱效应的土压力解，考虑土体内摩擦角对墙后土体滑倾面的影响，推导了挡土墙后主动土压力的计算公式。

目前，考虑土拱效应的墙后主动土压力研究中大多将土层假定为单层土［12-15］，然而，在实际地层中，土层并不是唯一的，而是沿着深度方向逐渐变化。为此，本文在前人研究基础上［16-18］，将考虑土拱效应的土压力计算公式扩展到多层土体，并以双层土为例，研究了“上软下硬”型地层和“上硬下软型”地层中的土压力分布规律，有助于深入认识土拱效应对墙后主动土压力分布规律的影响。

1  考虑土拱效应的单层土墙后主动土压力

1.1  挡土墙后土体滑裂面

如图1所示，分析墙后土楔体的受力，假定挡土墙墙背直立，墙后填土水平，δ为墙土摩擦角，φ为土体内摩擦角，β为墙后滑裂面倾角，q为墙后均布荷载，P为主动土压力合力，W为墙后土楔体的重力。

水平方向上力的平衡方程为

Pcosδ－Rcos（π2+φ－β）=0（1）

竖直方向上力的平衡方程为

Psinδ－Rsin（π2+φ－β）－W－qHcotβ=0（2）

其中，

W=12γH2cotβ（3）

将式（3）代入（2），得到：R=（12γH2+qH）cotβ－Psinδsin（π2+φ－β）（4）

P=（12γH2+qH）cosβsin（β－φ）sinβcos（β－φ－δ）（5）

为求主动土压力，用微分学中求极值的方法求P的最大值，令dP/dβ=0，得到：

β=arctantan2φ+tanφtan（φ+δ）+tanφ（6）

1.2  挡土墙后主动土压力求解

以一个典型的挡土墙为例，取微段进行受力分析，其受力分析模型可以大致概化为图2所示。假定挡土墙墙背直立，墙后填土水平，σh为土体微元的水平受力，τ1为水平单元的竖向受力，dy为土体微元的竖向长度，τ2为滑裂面受到的切应力，r为滑裂面受到的正应力，σav+dσav为作用于水平微分单元底面的平均竖向应力，H为墙体高度，y为土体微元段所处深度。

根据水平土压力与竖直土压力的关系，可得水平土压力为

σh=Kwσav（7）

要求解水平土压力系数，需要获得侧土压力系数Kw和竖向平均土压力σav，本节先推导竖向平均土压力的计算公式。

根据受力平衡分析，水平方向上力的平衡条件为

σhdy+τ2cosβsinβdy－rsinβcosβdy=0（8）

根据土体单元的竖向受力平衡分析可得：σav（H－y）cotβ+dW－（σav+dσav）（H－y－dy）×cotβ－τ1dy－τ2dy－rdycosβsinβ=0（9）

式中：dW为土体微元自重。根据土体重度定义，可得：dW=［（H－y）cotβ+（H－y－dy）cotβ］dy2γ（10）

式中：γ为土体自重。将公式（10）代入公式（9）后整理，略去二阶量，可以得到：dσavdy=γ+1H－y［σav－r－（τ1+τ2）tanβ］（11）

将公式（7）中的σh=Kwσav，以及τ1=σhtanδ，τ2=rtanφ，代入公式（8）可得：r=Kwsinβcosφsin（β－φ）σav（12）

结合公式（11）和公式（12）可得：dσavdy=［1－sinβcos（β－φ－δ）cosβcosδsin（β－φ）Kw］·σavH－y+γ（13）

令（13）式中的sinβcos （β-φ-δ）cosβcosδsin （β-φ）=α，则公式（13）可以简写为

dσavdy=1－αKw·σavH－y+γ（14）

对式（14）积分，并利用边界条件y=0时，竖向土压力σav等于地表压力q，可得：σav=（q－γαKw－2H）（H-yH）αKw－1+γαKw－2（H－y）（15）

注意到上式中只有Kw未知，因此问题转换为求土压力系数Kw。

1.3  圆弧拱形的侧土压力系数

根据摩尔库伦准则，土体任意一点受到的剪应力τ和水平应力σh与最大主应力σ1和最小主应力σ3的关系分别为

τ=（σ1－σ3）sinθcosθ（16）

σh=τcotθ+σ3（17）

式中：θ为应力偏转角，σ1为最大主应力，σ3为最小主应力。联立公式（16）和（17），并令σ3/σ1=Ka，可得：σhσ1=cos2θ+Kasin2θ（18）

根据应力状态分析易得Ka=（1-sinφ）/（1+sinφ）。由于σh-σ3=σ1-σv，因此有式（19）成立：σvσ1=sin2θ+Kacos2θ（19）

考虑土拱效应时，土压力系数Kw是土体微段水平应力与平均竖向应力之比，即σh/σav，而不是σh/σv，因此不能简单采用式（18）与式（19）比值得到。根据如上所述，考虑土拱效应的侧土压力系数为

Kw=σhσav=σh/σ1σav/σ1=1σav/σ1（cos2θ+Kasin2θ）（20）

要求解式（20）得到土压力系数，需要知道两个未知量，即应力偏转角θ和平均竖向应力与最大主应力的比值σav/σ1。

当墙体光滑时，θ=90°；当墙土摩擦角充分发挥时，θ=45°+φ/2。但是实际工程中，墙土摩擦角往往并未充分发挥。Paik等［18］考虑到墙土摩擦角往往小于土体内摩擦角，采用Mohr Circle计算获取拱角主应力偏转角θ：θ=π2－12arcsin（sinδsinφ）+δ2（21）

另一方面，任意位置微分单元竖向应力平均值都可表示为

σavσ1=∫B0σmvσ1dxB（22）

式中：σmv为土条微段的任意一点受到的竖向土压力，B为圆弧圆心距离挡土墙的水平距离（图3）。假设土拱的形状为圆弧状，根据公式（19），可以得到圆弧上任意一点的水平应力σmh和竖直应力σmv为

σmh/σ1=cos2ψ+Kasin2ψσmv/σ1=sin2ψ+Kacos2ψ（23）

式中：σmh为任意圆弧拱任意微分单元上的水平方向应力；σmv为圆弧拱任意微分单元上的竖直方向应力；ψ为圆弧拱任意位置的中心线与水平方向的夹角。

根据相似三角形可以很容易得出：ψ=arccos（B－xBcosθ）（24）

根据图3，土拱宽度L与圆弧圆心距离挡土墙的水平距离B的关系为

L=cotβcot（π/4+φ/2）B（25）

将式（25）代入式（24）可得：ψ=arccos（1－xLcotβcot（π/4+φ/2））cosθ（26）

将式（26）代入式（23），可以得到：σmvσ1=sin2{arccos［（1－xLcotβcot（π/4+φ/2））cosθ］}+Kacos2{arccos［（1－xLcotβcot（π/4+φ/2））cosθ］}（27）

注意到式（23）中所有的参数都在求解过程中得到具体的值，只有x为随着圆弧拱的位置而变化的横坐标，将式（27）代入式（22），可以得到任意位置微分单元竖向应力平均值σav/σ1，进而可以由式（20）得到考虑土拱效应的侧土压力系数Kw，再代入公式（15）和公式（7），即可得到墙后主动土压力。

2  多层土墙后主动土压力计算

如图4所示，对于多层土，由于每一层土体的重度、内摩擦角、墙土摩擦角等参数不尽相同，根据前述推导过程，可以知道每一层土体的侧土压力系数Kw都是不同的。因此，在土层分界处由于侧压力系数的突变，分界处的土压力也会出现突变，为此，需要计算分界面位置处上下的土压力。以A点计算为例，考虑土拱效应后上层土体中A点的墙后主动土压力σUpperA计算公式为

σUpperA=Kw1［（γ1α1Kw1－2H）（H-H1H）α1Kw1－1+γ1α1Kw1－2（H－H1）］（28）

下层土体中A点的主动土压力σLowerA为

σLowerA=Kw2σUpperAKw1－γ2α2Kw2－2（H－H1）+γ2α2Kw2－2（H－H1）（29）

对于第二层土中的其他任意位置处的土压力分布计算公式可以表达为

σ=Kw2（σUpperAKw1－γ2α2Kw2－2（H－H1）（H-yH）α2Kw2－1+γ2α2Kw2－2（H－y）（30）

3  算例分析

3.1  算例1，上软下硬型土层

本节考虑墙体后土层为“上软下硬型”时主动土压力的分布规律。假定墙后土层为双层土体，墙高20 m，上层土厚度为10 m，分别考虑墙后墙土摩擦角充分发挥时与部分发挥时两种情况，并将理论解和数值解进行对照，以便验证结果的准确性。

3.1.1  理论验证

为了验证所提理论解的合理性，在PLAXIS-2D中建立了一个相同尺寸的基坑开挖模型。土体参数上层土取内摩擦角为10°，下层土内摩擦角为20°，开挖深度为20 m，计算双层土体墙后主动土压力。如图5所示，可以发现借助有限元计算的土压力和采用式（30）计算得到的土压力可以较好地吻合在一起，在变化趋势上也颇为一致，这说明本文提出的理论解可以计算考虑土拱效应的多层土体墙后主动土压力。

3.1.2  墙土摩擦角充分发挥

当墙后土体充分发挥时，土体内摩擦角φ与墙土摩擦角δ相等，此时双层土体的墙后主动土压力分布规律如图6所示，可以发现在土体分界处土压力会出现突减的现象。此外，由图可知，随着土体内摩擦角的增大，墙后的主动土压力逐渐减小，这主要由于内摩擦角增大时，降低了土体的侧压力系数，当竖向压力不变时，根据σh=Kaσv可得侧压力系数越小，横向主动土压力越小。当上下土层的参数相同时，得到的土压力分布与单层土相同，这验证了本文提出的多层土公式的正确性。

3.1.3  墙土摩擦角部分发挥

图7给出了当墙土摩擦角部分发挥时（δ<φ），墙后主动土压力分别随着上层土体的墙土摩擦角和下层土体的墙土摩擦角变化的规律，可以发现当下层土体的参数保持不变，上层土体的墙土摩擦角逐渐增大时，上层土的墙后主动土压力逐渐增大，而下层土的土压力逐渐减小；当上层土的土体参数保持不变时，上层土的墙后主动土压力不会随着下层土的墙土摩擦角变化，然而下层土的墙后主动土压力会产生较大变化，最明显的一个趋势在于当下层土的墙土摩擦角部分发挥时，下层土体的主动土压力最大值不会出现在土体分层处，而是由所下移，且最大土压力会略大于墙土摩擦角充分发挥时的值。

3.2  算例2，上硬下软型土层

3.2.1  理论验证

同样，在PLAXIS-2D中建立与算例1中相同的数值模型。上层土体内摩擦角取40°，下层土体内摩擦角取20°。图8为上硬下软型土层的墙后主动土压力数值解与理论解之间的对比。可以发现无论在量值上还是在变化趋势上，所提理论解均能很好地与有限元模拟数据吻合在一起，这反映了所提理论解的准确性。

3.2.2  墙土摩擦角充分发挥

以“上硬下软型”土层为例，研究墙土摩擦角充分发挥时墙后主动土压力的分布规律。图9给出了此时的墙后主动土压力分布规律，可以发现当土层分布为“上硬下软”时，土层分界处的主动土压力会出现突增现象，这与上软下硬型土层的分布规律是相反的，但是随着上层土的内摩擦角逐渐增大，墙后主动土压力逐渐减小。

3.2.3  墙土摩擦角部分发挥

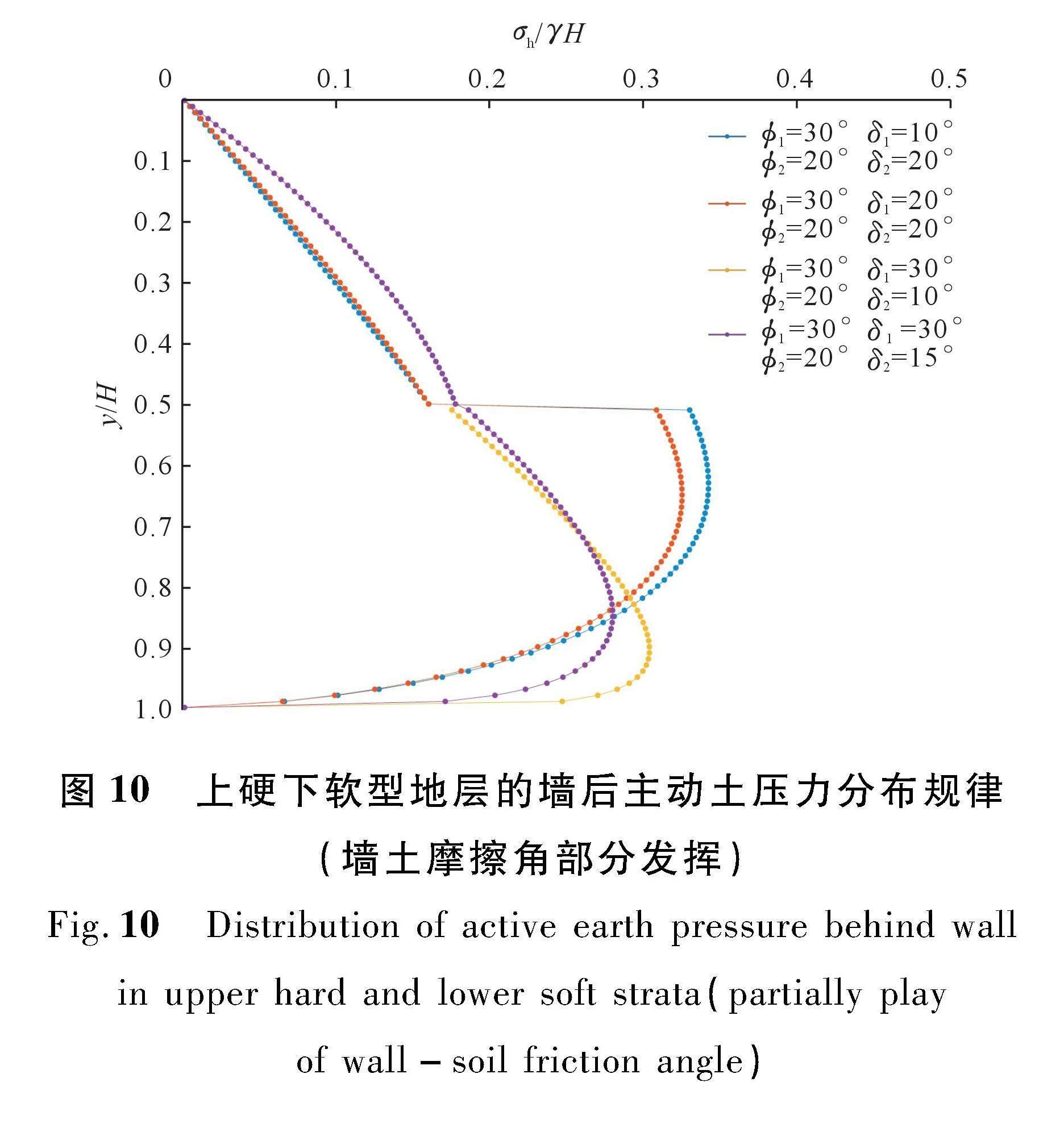
图10为当墙土摩擦角部分发挥时墙后主动土压力的分布规律。可以发现，当下层土体参数保持不变，上层土体的墙土摩擦角逐渐增大时，上层土的墙后土压力变化较小，但是下层土体主动土压力逐渐减小；当上层土体参数保持不变时，随着下层土体墙土摩擦角的增大，下层土的最大土压力位置逐渐上移，这与“上软下硬型”土层的分布规律是一致的。

4  结 论

本文结合传统土拱效应理论，推导建立了一种多层土体的墙后主动土压力分布计算方法，并以两个典型土层为例，通过数值模拟方法验证了所提计算方法的适用性和合理性。同时，讨论了两种不同土层条件下墙土摩擦角充分发挥和未充分发挥时的墙后主动土压力变化规律，主要结论如下：（1） 提出了考虑土拱效应的多层土体墙后主动土压力计算方法，通过与数值模拟结果对比，验证了该方法的合理性和适用性。

（2） 在“上软下硬型”土层中，当墙土摩擦角充分发挥时，上层土体的主动土压力受到的影响更大，且随着内摩擦角的逐渐增大，墙后土压力逐渐减小；当墙土摩擦角部分法发挥时，下层土体的主动土压力受到的影响更大，且下层土体的最大应力出现位置会随着下层土体墙土摩擦角的增大而逐渐上移。

（3） 在“上硬下软型”土层中，当墙土摩擦角充分发挥时，随着内摩擦角的增大墙后主动土压力逐渐减

小；当墙土摩擦角部分发挥时，随着上层土墙土摩擦角

的逐渐增大，下层土的主动土压力逐渐减小，当下层土的墙土摩擦角逐渐增大时，下层土体的主动土压力最大作用点逐渐上移。

（4） 墙土摩擦角充分发挥时，上层土的墙后土压力受到土体内摩擦角影响更大；而当墙土摩擦角部分发挥时，下层土体的墙后土压力受到墙土摩擦角变化影响更大。

参考文献：［1］  梅国雄，宰金珉.考虑变形的朗肯土压力模型［J］.岩石力学与工程学报，2001，20（6）：851-854.

［2］  汪丁建，童龙云，邱岳峰.降雨入渗条件下非饱和土朗肯土压力分析［J］.岩土力学，2013，34（11）：3192-3196.

［3］  丁兆锋，吴沛沛，刘会娟，等.库伦主动土压力的通用解法［J］.铁道工程学报，2016，33（8）：55-58.

［4］  柯才桐，陈奕柏，谢洪波，等.库伦土压力合力作用点高度解析解［J］.水电能源科学，2014，32（5）：91-95.

［5］  李海珍，李永刚.RB模式下挡土墙非极限状态主动土压力分析［J］.人民长江，2016，47（18）：92-95.

［6］  吕涛，齐美苗，彭良泉.抗滑桩的土拱效应及数值模拟［J］.人民长江，2007，38（1）：42-45.

［7］  TERZAGHI K.Record earth pressure wall testing machine［J］.Engineering News Reeord，1932，109：365-369.

［8］  TERZAGHI K.Large retaining wall tests Ⅰ：pressure of dry sand［J］.Engineering News Reeord，1934，112：136-140.

［9］  TERZAGHI K.A fundamental fallacy in earth pressure computations［J］.Journal of Boston Society of Civil Engineering，1936，23：71-88.

［10］FINN W D L.Boundary value problems of soil mechanics［J］.Journal of the soil Mechanics and Foundations Division，ASCE，1963，89（SM5）：39-72.

［11］WANG W L，YEN B C.Soil arching in slopes［J］.Journal of Geotechnical Engineering Division，ASCE，1974，104（GT4）：493-496.

［12］应宏伟，蒋波，谢康和.考虑土拱效应的挡土墙主动土压力分布［J］.岩土工程学报，2007，174（5）：717-722.

［13］苏培东，张海传，戚宗轲，等.不同截面抗滑桩的土拱效应对比研究［J］.防灾减灾工程学报，2023，43（2）：405-412.

［14］吴明，彭建兵，徐平，等.考虑土拱效应的挡墙后土压力研究［J］.工程力学，2011，28（11）：89-95.

［15］蒋波，应宏伟，谢康和.挡土墙后土体拱效应分析［J］.浙江大学学报，2005，39（1）：131-136.

［16］刘金慧，屈克军，丁万涛，等.硬塑粉质黏土层深埋马蹄形隧道开挖土拱演化分析［J］.人民长江，2022，53（1）：189-197.

［17］代云霞.饱和软黏土静止土压力系数试验探讨［J］.人民长江，2017，48（增2）：240-243.

［18］PAIK K H，SALGADO R.Estimation of active earth pressure against rigid retaining walls considering arching effect［J］.Geoteehnique，2003，53（7）：643-653.

（编辑：郑 毅）

Study on active earth pressure mode behind multi-layer soil considering soil arching effect

LI Wenbiao，LYU Yanhao，YOU Longfei

（China Railway Siyuan Survey and Design Group Co.，Ltd.，Wuhan 430063，China）

Abstract：

The soil arching effect is widely proven to be in geotechnical engineering.However，research on the soil pressure caused by the soil arching effect is currently limited to single-layer soil，and the distribution of active soil pressure behind multi-layer soil is still unclear.Therefore，based on the soil arching effect theory，this article proposed a solution for nonlinear active earth pressure behind retaining walls of multi-layer soil，and studied the influence of internal friction angle and friction angle between wall and soil on the distribution pattern of active earth pressure based on two typical strata.The results show that the proposed solution can effectively describe the distribution of active earth pressure behind multi-layer soil.The calculation results are basically consistent with the numerical simulation results.When the parameters of the upper and lower soil layers are consistent，the proposed solution can degenerate into a soil pressure calculation model of single soil layer.When the friction angle between wall and soil is fully utilized，the soil pressure behind the upper soil wall is significantly affected by the internal friction angle of the soil，while the friction angle between wall and soil is partially utilized，the soil pressure behind the lower soil wall is more affected by the wall soil friction angle.

Key words：

soil arching effect; retaining wall; multi-layer soil; active earth pressure