旭龙电站尾水调压室洞间岩柱围岩宏细观特性分析

李冬冬 陈捷平 吴秋波 孙海清

收稿日期：2023-04-23；接受日期：2023-06-26

基金项目：国家自然科学基金项目（52079097）

作者简介：李冬冬，女，高级工程师，博士，主要从事地下洞室工程研究。E-mail：lidongdong3@cjwsjy.com.cn

Editorial Office of Yangtze River. This is an open access article under the CC BY-NC-ND 4.0 license.

文章编号：1001-4179（2024） 06-0194-10

引用本文：李冬冬，陈捷平，吴秋波，等.旭龙电站尾水调压室洞间岩柱围岩宏细观特性分析

［J］.人民长江，2024，55（6）：194-203.

摘要：为了将连续和非连续分析方法耦合用于地下厂房围岩稳定性分析，提出了一种基于软硬混合平行黏结模型的细观参数快速标定法，可根据给定岩石的宏观力学参数快速给出其颗粒流模型细观接触参数；在此基础上，构建了基于颗粒离散元PFC 3D与有限差分FLAC 3D耦合的旭龙地下电站尾水调压室三维离散-连续耦合分析模型，研究了开挖期尾水调压室洞间岩柱围岩变形与破坏宏细观特性，以及检修期间侧向水压力对洞间岩柱稳定性的影响。结果表明：检修期间尾水调压室水压力引起的围岩变形与应力增量变化是极小的，但洞间岩柱上半段22.7 m的高度存在塑形贯通区，局部稳定性较差，有必要在工程建设期开展尾水调压室及尾水支洞岩墩塑性贯通区专项支护方案研究，以确保旭龙地下电站工程的安全建设与运行。

关  键  词：尾水调压室； 洞间岩柱； FLAC 3D； 离散-连续耦合； 塑形贯通区

中图法分类号： TV731

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2024.06.027

0  引 言

水电站地下厂房正朝装机规模大、厂房跨度大、高边墙的超大型化方向发展。拟建在建的一大批水电站采用单机容量70万kW级别的机组，地下厂房跨度多达20余m、甚至超过30 m，高度多达50余m、最大已接近90 m［1-2］。主厂房、主变洞、尾水调压室等引水发电系统各洞室纵横交错布置，形成庞大、复杂的大规模密集地下洞室群［3-4］。考虑工程地质条件、主要枢纽建筑物布置、工程造价等因素，地下洞室群常采用集约布置理念，各大洞室间岩柱间距较小，可能影响岩柱与洞室群的局部或整体稳定性［5-6］。

实际工程中，洞室间距对围岩稳定性、支护设计和施工方案等具有重要影响［7-10］。以旭龙地下电站为例，尾水调压室及尾水洞具有开挖体型复杂、岔管较多、山体挖空率高的特点，尾水调压室洞间岩体厚度为16.0 m，高54.2 m，在开挖工况下存在岩柱破坏区贯穿的风险，危及围岩稳定性。检修工况下同一水力单元的两台机组检修、另一水力单元正常运行，调压室洞间岩柱将承担水压力，需要明确该工况时洞间岩柱的稳定性。

目前对于地下洞室群洞间岩柱的分析研究，常采用工程类比法和数值分析法。前者主要基于国内外已建地下厂房洞室群的洞室布置参数进行类比分析［11-12］，后者随着计算机技术发展已经被广泛应用到地下岩石工程领域的研究中。快速拉格朗日有限差分程序FLAC 3D和颗粒离散元程序PFC 3D均为美国ITASCA公司研发的大型仿真计算软件，前者属于连续介质力学法的范畴，可以模拟各类岩土体和结构单元（锚杆、锚索、衬砌等）的变形与受力状态，得到了国内外的广泛应用和认可，积累了丰富的工程经验［13～15］；后者则是从非连续介质力学法（离散元）的角度研究介质细观力学特性和行为的工具，目前鲜少用于大型地下洞室群围岩稳定分析与研究。二者的程序可在计算过程中相互传输变量并拥有共同的二次开发语言FISH［16-18］。

本文集连续-非连续分析方法之所长，基于PFC 3D-FLAC 3D离散-连续耦合分析方法，构建旭龙地下电站尾水调压室三维离散-连续分析模型，重点分析开挖期和检修期受侧向水压力时，尾水调压室洞间岩柱的变形受力特征、破坏区分布、微裂纹发育规律等宏-细观特性，以期为施工期尾水调压室及尾水支洞岩墩塑性贯通区专项支护方案提供参考。

1  旭龙尾水调压室简介

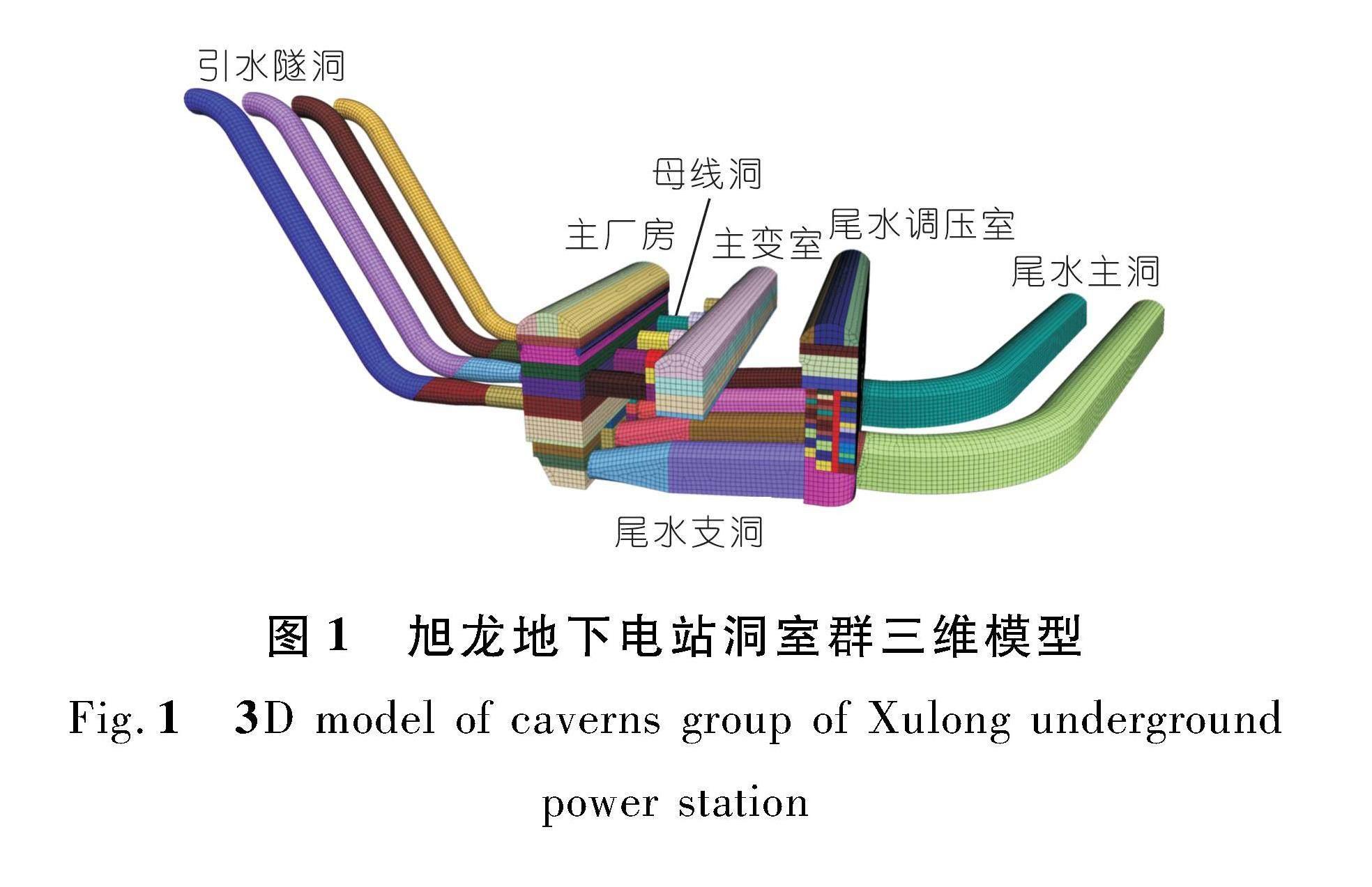
旭龙水电站位于云南省德钦县与四川省得荣县交界的金沙江干流上游河段，是金沙江上游河段“一库十三级”梯级开发方案中的第12级，是西电东送骨干电源点之一。地下厂房集中布置在右岸，安装4台单机容量为600 MW的混流式水轮发电机组，装机容量为2 400 MW。主厂房、主变室和尾水调压室等三大洞室平行布置（图1），主厂房与主变洞洞间岩体厚度为40.0 m，主变洞与尾水调压室洞间岩体厚度为30.5 m。

尾水调压室为阻抗式、长廊型，调压室前尾水隧洞为一机一洞，调压室后为两机一洞布置，尾水调压室开挖尺寸为161.5 m×19.1 m（20.0 m）×87.6 m。尾水调压室外侧端墙距岸边240.0 m，洞室埋深290.0～410.0 m，调压室轴线方向NE55°。围岩以灰白色中细粒花岗岩为主，近岸侧为灰黑色斜长角闪岩脉体（图2）；花岗岩岩质新鲜、坚硬，构造不发育，岩体较完整—完整，单轴饱和抗压强度90～110 MPa，岩体声波测试Vp均值为5.29 km/s；斜长角闪岩脉体长英质含量较高，岩质较坚硬—坚硬状，岩体完整性差—较完整，单轴饱和抗压强度80～90 MPa，岩体声波测试Vp均值为4.67 km/s。

根据尾水调压室下游54.0 m处地应力测试孔的试验成果，下游范围内最大水平主应力范围主要为4.1～32.5 MPa，最小水平主应力范围主要为2.8～18.1 MPa，最大水平主应力为中等—高地应力水平。最大水平主应力方向为N27°～47°E（平均N38°E），与洞室轴线夹角8°～28°。

尾水调压室围岩花岗岩为块状构造，斜长角闪岩脉体以次块状构造为主，岩性分界面走向355°～5°，倾向W，倾角70°～80°，岩性界线与调压室轴线夹角50°～60°。地表f3断层斜穿尾水调压室中部，断层走向30°，倾向300°，倾角75°～80°，断层走向与尾水调压室轴线夹角25°，断层带宽0.2～0.3 m，构造岩主要为碎裂岩，原岩为花岗岩或斜长角闪岩，较破碎，胶结一般；主断面为厚0.1～2.0 cm断层泥，局部为钙质及岩屑。尾水调压室洞室围岩Ⅱ类围岩长度为125.0 m，Ⅲ类围岩洞室长度为25.0 m，Ⅱ类围岩占83%，Ⅲ类围岩占17%。

2  尾调室离散-连续耦合模型

2.1  PFC 3D-FLAC 3D耦合分析原理

PFC 3D-FLAC 3D离散-连续耦合分析是指将FLAC 3D连续区域与PFC离散区域的接触面指定为PFC的墙体，采用等效力方法将颗粒作用于墙上的接触力和接触弯矩分配到墙面的顶点上，墙体顶点则附着于实体单元的网络点或结构单元的节点上，由此实现了墙体顶点运动与实体单元网格点（或shell单元节点）的同步运动。PFC墙体传递来的力和弯矩，参与连续域的FLAC 3D模型计算分析进程，连续域节点的变形也带动了墙体的运动，进而将位移和速度通过墙传递到离散域中的颗粒。通过上述各项值的不断更新，改变模型几何参数以及单元或结构单元的刚度。

假设一个球与一个三角形墙面接触，C为接触点，CP为墙面上距离C点最近的点，从CP到三角形的顶点采用重心插值法外推。三角形顶点为Vik，（i=1，2，3，k=1，2，3），通过链接3个顶点与CP，得到3个三角形（图3），面积分别为Ai，3个三角形的总面积为A=A1+A2+A3。

顶点加权因子定义为采取与顶点相对三角形面积除以三角形的总面积，ωi=Ai/A，等式ωi=1恒成立，以保证从CP到顶点外推值总和等于CP处的值。当完整计算模式关闭时，接触力和平动刚度也通过这种方式外推到节点处，但由于顶点力和潜在的顶点力矩可能会不平衡，重心外推不能确保外推力和力矩与CP位置的瞬时接触力和力矩一致。

假定Ri（i=1，2，3）为CP到3个顶点的向量，Ri=Vik－CP，施加在每一个网格点或节点的力为Fi（i=1，2，3），施加在接触点C上的力为F，接触点处由于黏结产生的力矩为Mb。由于接触点C和接触平面上点CP可能不共点，所以作用在接触平面上的总力矩为

M=Mb+C－CP×F（1）

当全运算模式处于活动状态时，耦合方案确定完全一致的等效力系统，即：3i=1Fi=F（2）

Ri×Fi=M（3）

n为三角形的单元法向向量，沿着三角面的剪切力矢量为Fs，即：Fs=F－F·n（4）

切向单位矢量为

S=FsFs（5）

局部坐标系中x轴的方向与法向n的方向一致，y轴的方向与剪切方向s方向一致，由于CP点在三角面上，Ri在z方向上均为0，即Ri，z=0。这种简化可以直接确定局部坐标系统中顶点力和力矩的x、y、z方向上分量Fi，x、Fi，y、Fi，z，即：Fi，x=Fx

Fi，y=Fy

Fi，z=Fz=0（6）

Ri，y×Fi，z－Ri，z×Fi，y=Mx

Ri，z×Fi，x－Ri，x×Fi，z=My

Ri，x×Fi，y－Ri，y×Fi，x=Mz（7）

由于之前的重点加权项使得力的y分量分布Fi，y=ωiFy，因此在三角形平面中最大接触力的方向上施加重点加权。这个假设的结果导致以下2个方程有3个未知数：Fi，z=0（8）

Ri，y×Fi，z=Mx+Ri，z×Fi，y（9）

对于这种欠正定方程组，在无约束条件下有无穷多解。控制方程式不能明确地确定约束的性质来找到一个等效的系统。因此为获得一个特解，需要提供额外的约束条件，紧随着实体单位或结构单元运动方程，以根据相应的网格点节点位置和速度设置墙面顶点的位置和速度。

Ri，y×Fi，z=0（10）

式（10）可解释为：如果开始时在局部z方向上的每个网格点或节点施加力，则从CP指向局部坐标系中的三角形顶点向量的点积总和为0。所得到的合力随后被转换为全局坐标系统并应用到适当的区域网格点或结构单元节点。此时触发区域和结构单元更新。在区域和结构元件更新期间，对网格节点、结构单元节点添加刚度。当接触处存在旋转刚度时，这些也必须考虑到以确保稳定性。通过将旋转刚度的大小除以Ri来确定等效的平移刚度。

2.2  尾调室整体模型与耦合模型

通过FLAC 3D建立的尾水调压室数值分析模型其范围为527.3 m×450.1 m×524.5 m（X×Y×Z），其中调压室开挖尺寸为161.5 m×19.1 m（20.0 m）×87.6 m（长×宽×高）。计算模型及网格划分见图4：划分单元262 403个、节点147 642个，x轴平行于尾水调压室纵轴线，指向山体内部为正；y轴顺水流向，向下游为正；z轴铅直向上，底部高程为2 101.0 m。模型包括尾水调压室以及部分尾水支洞与尾水主洞。同时考虑了f3断层及不同岩层分布产状。尾水调压室自上而下共分22层开挖，为了保护洞间岩柱的稳定性，开挖到洞室中下部时先开挖岔管部分（第5期）、后掏空2.5 m宽的岩柱（第6期），再按照2 m每层的厚度逐层向下进行开挖。

分别在尾水调压室洞间岩柱的顶部、中部和底板处设置耦合区域（图5）。耦合区域1和2沿尾水调压室纵轴线方向贯穿岩柱，长16.0 m，横截面积为2.0 m×2.0 m，分别生成耦合墙体256个、颗粒22 145个，颗粒半径为7.5～10.0 cm，主要用于研究洞间岩柱在开挖过程中的变形与破坏宏细观特性。

耦合区域3设置在底板附近，主要用于研究检修工况下洞间岩柱承担单方向水压力时，洞间岩柱边墙中下部的围岩宏细观特性，耦合区域尺寸为4.0 m×3.0 m×4.0 m（X×Y×Z），生成耦合墙体192个、颗粒12 060个，颗粒半径为7.9～11.5 cm。颗粒间为平行黏结接触模型，颗粒与墙体之间为线性接触模型。

2.3  岩体宏-细观力学参数快速标定

在室内、现场试验成果的基础上，结合具体工程地质条件，确定地下厂房区主要岩石（体）和结构面的物理性质和力学参数建议值见表1和表2。地下厂房洞室群区域地层岩性主要为花岗岩、混合岩。综合原位试验成果、洞室群开挖卸荷及可能存在的裂隙等不利地质构造等因素，围岩稳定分析时，各岩层和结构面所采用的物理力学参数建议取低值。

在采用PFC 3D-FLAC 3D离散-连续耦合分析方法研究洞室群岩体宏细观力学特性之前，首先需要解决的、也是关键问题之一的是PFC颗粒流模型细观力学参数的选取。实际岩体中都是由刚度显著不同的颗粒构成的，其变形过程中不同颗粒之间可以协调变形，而采用均质的、相同黏结和刚度参数时，则无法反映这种现象。

为此，可以通过混合黏结模型参数来更真实地逼近实际情况。假定岩石试样由软硬两种颗粒接触构成，其中40%的接触为软接触。软接触模量为硬接触模量的0.1倍，黏结强度为硬接触黏结强度的0.08倍。FISH语言实现方法为：遍历模型所有接触，对于任一接触，定义一个介于0和1的随机数，当随机数的值小于0.4时，则赋予该接触为软接触的参数。通过上述基于混合平行黏结模型的细观参数快速标定法，确定旭龙地下厂房区岩体宏观参数对应的细观接触参数取值。下面以厂区某花岗岩为例阐述颗粒流模型细观参数快速标定的过程。

待标定的花岗岩宏观试验参数为：拉伸弹性模量40 GPa，压缩弹性模量40 GPa，泊松比0.23，单轴抗压强度90 MPa，单轴抗拉强度9 MPa，拉压比0.1。

用于标定细观参数的PFC颗粒流模型如下：宽2.0 m、高4.0 m，粒径在1.0～2.0 cm间随机分布，初始平衡得到模型后，修改参数并激活接触，开展各种数值模型试验，获取试样的宏观力学参数，并不断调整参数直至完成标定。

岩石试样的宏观力学试验特性与颗粒流模型数值试验结果的对应关系如表3所列。

（1） 将线性有效接触模量emod保持为相对较小的数值（0.1 MPa），依次设置平行黏结有效模量pb_emod为60，80，100，120 GPa，分别获取直接拉伸条件下的应力-应变曲线（图6），试样的宏观拉伸弹性模量即为峰值应力与峰值应变的比值。拟合得到拉伸弹性模量与平行黏结模量pb_emod的关系，将待标定岩石试样的拉弹性模量Et=40 GPa，代入趋势线公式（图7）Et=0.385 8x+ 2.172 2，求出平行黏结模量pb_emod的值为98.50 GPa。

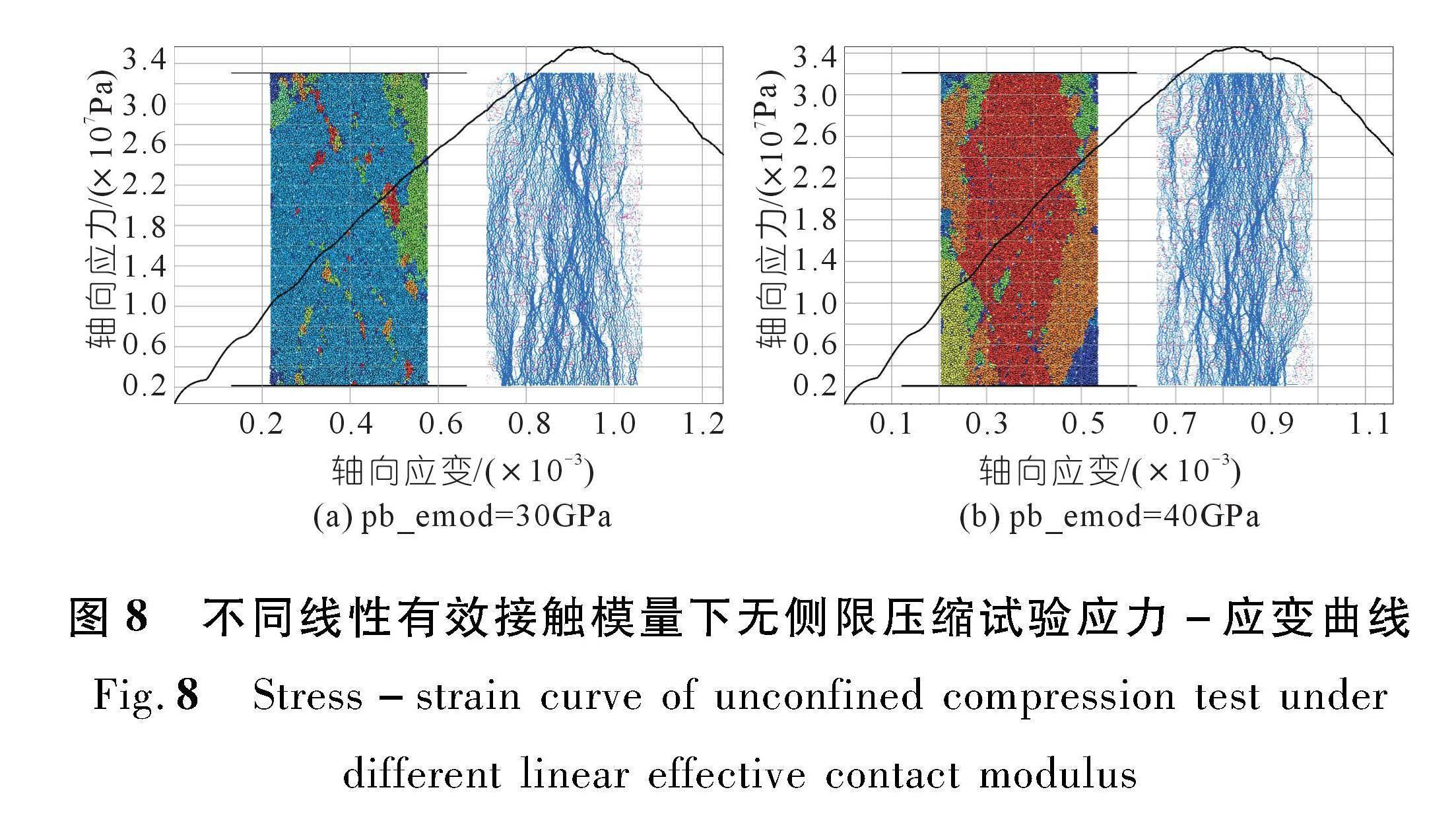
（2） 固定平行黏结模量pb_emod的值为98.5 GPa，采用无侧限压缩试验标定线性接触模量，研究线性有效接触模量emod对压缩模量的贡献。依次设置线性有效接触模量emod为10，15，20，25，30，40 GPa，分别获取单轴压缩时试样的应力-应变曲线（图8），压缩弹性模量即为峰值应力与峰值应变的比值。拟合得到压缩模量与线性有效接触模量emod的线性取值关系Ec=0.425 1x+27.723。根据待标定试样的压弹性模量Ec=40 GPa，求出线性有效接触模量emod的值为23.52 GPa。

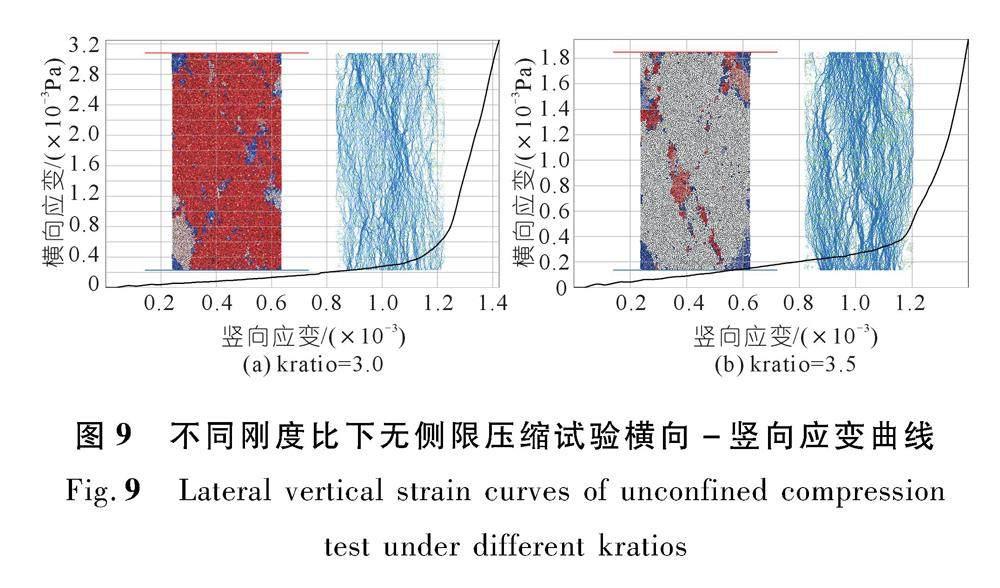
（3） 固定线性有效接触模量emod为23.52 GPa和平行黏结模量pb_emod为98.50 GPa，假定平行黏结分量与线性接触分量的刚度比kratio相同，研究刚度比与宏观泊松比的对应关系。依次设置刚度比为1.5，2.0，2.5，3.0，3.5的情况进行单轴压缩试验，取名义应变（峰值强度一半对应的应变）所处位置计算泊松比（图9）。拟合得到岩石试样泊松比与刚度比kratio的对应关系μ=0.074 1x+0.024 7。将岩石实际泊松比μ=0.23代入，即可求得刚度比kratio的值为2.77。

（4） 当法向与切向黏结强度比值越大，试样越容易出现剪切破坏；当比值越小，试样越容易出现脆性破坏（图10）。应根据实际试验中的岩石破坏情况，近似在0.5～2之间取值。综合数值模型试验与试验机结果，此处黏结强度比取为1.2，确定后固定该比值不变。

假定切向黏结强度的取值为10 MPa，根据法向与切向黏结强度比1.2，求得法向黏结强度为12 MPa，二者称为基准黏结强度。在基准黏结强度的基础之上，依次同时乘以黏结强度变化系数3，6，8，10，12.5，15，18，分别得到不同的单轴抗压强度。拟合得到岩石试样单轴抗压强度σc与黏结强度变化系数间的对应关系为σc=6.936 4x+0.336 7。岩石试样实际抗压强度为90 MPa，求得放大系数为12.926，再乘以基准黏结强度10 MPa，即可得到法向黏结强度为15.512 MPa，切向黏结强度为12.926 MPa。

（5） 根据上述步骤得到了该花岗岩颗粒流模型细观接触参数如下：平行黏结模量pb_emod为98.50 GPa，线性有效接触模量emod为23.52 GPa，刚度比kratio为2.77，法向黏结强度pb_ten为15.512 MPa，切向黏结强度pb_coh为12.926 MPa。其他参数：摩擦角pb_fa为45°，半径乘子pb_rmul为1.0，弯矩贡献系数pb_mcf为1.0，法向应力更新模式lin_mode为1，摩擦系数fric为0.5。

（6） 由于各参数间会相互交叉影响，按照上述参数试算，岩石试样拉弹性模量为31.398 GPa，压弹性模量为33.90 GPa，单轴抗拉强度为8.086 MPa，单轴抗压强度为90.257 MPa，拉压比为0.089 6。模量比待标定值略偏小，此时可以按照实际数据进行微调，提高平行黏结模量与线性有效接触模量，并适当降低黏结强度（表4）。通过若干次试算，最终标定得到的参数（表5），已经非常接近岩石真实的宏观力学参数。

3  开挖期洞间岩柱宏细观特性

第6期开挖后洞室围岩变形最大值22.0 mm出现在两侧边墙，方向指向洞内。洞间岩柱顶端以竖直

向上的变形为主，第6期开挖后位移最大值9.5 mm出现在岩柱顶端转角处，岩柱两侧位移较小。随后在尾调室下半段开挖过程中，以每层2.0 m左右的高度向下开挖，岩柱顶端位移持续增大，岩柱两侧的变形随高度降低而呈线性减小趋势。到开挖完毕后，洞间岩柱顶端最大位移为14.6 mm，两侧位移矢量相对岩柱中心轴基本呈对称分布（图11）。

除洞间岩柱顶端临近上部开挖临空面的区域外，尾水调压室顶拱、上部边墙以及岔管的开挖未在洞间岩柱产生围岩破坏区。下半段洞室边墙开挖过程中洞间岩柱产生了破坏区，并在后续开挖时产生了塑性区贯通（图12）。到开挖完毕时岩柱上半段22.7 m的高度存在塑形贯通区，下半段31.5 m高度范围内塑性区深度呈线性逐渐降低，中间仍保留有一定范围的弹性区，到岩柱底板处围岩塑性区几乎为0。本文中围岩破坏区类型的释义如下：shear为剪切破坏单元；tension为张拉破坏单元；n为now，指应力正位于屈服面；p为previous，指曾进入屈服状态但现已退出；下同。

耦合区域1位于尾水调压室洞间岩柱顶端，临近上部洞室开挖临空面，围岩破坏区发展较快且深度较大，在第6期开挖后即出现了贯通塑性区，相应在PFC 3D耦合颗粒模型内部发育了分布均匀的微裂纹（图13）；后续开挖过程中持续在耦合区域1内产生了一定程度的破坏，到开挖完毕时微裂纹单元数达到了6 190个。

耦合区域2位于尾水调压室洞间岩柱中部，与尾水调压室最后一期开挖的岩体相邻，因此受上部洞室开挖影响相对较小，在尾调室第18期开挖以前，虽有少量微裂纹发育，但未在该区域内产生破坏单元。开挖完毕后，洞间岩柱两侧对称产生了各5.3 m左右的塑性区，中间5.3 m为弹性区。PFC 3D耦合颗粒模型两侧的微裂纹集中发育、密度较大，中间微裂纹密度相对较小（图14），整个开挖过程共出现微裂纹单元2 536个。

4  侧向水压力对岩柱稳定影响

尾水调压室检修工况下同一水力单元的两台机组检修，另一水力单元正常运行，调压室间洞间岩柱将承担水压力。经水力过渡过程计算，调压室最高涌浪为2 170.35 m。计算出底板处最大水压力为1 595 106 Pa，选取承受水压力的尾调室岩壁表面，利用梯度应力在该表面施加随Z方向线性递减的法向应力，来模拟呈三角形分布的水压力（图15）。

选取1-1′和2-2′作为典型剖面研究水压力对洞室变形和受力的影响（图16），其中2-2′剖面为理论上的水压力集中作用面。

水压力引起的调压室典型剖面增量位移分布见图17。尾调室一侧施加水压荷载后，随着高程的降低，尾调室水压引起的围岩位移增量逐步增大。从山体外到山体内，随着远离荷载作用面，尾调室水压引起的岩柱位移增量逐步减小。此外，尾调室岩柱变形主要位于施加荷载一侧的边墙中下部，增量位移一般为0.1～0.7 mm，最大值为0.75 mm，位于高程2 126 m附近。

尾水调压室水压力作用前后，无水压力时洞间岩柱最大主应力出现在山内侧的岩柱与底板交汇处，局部拉应力达到0.195 MPa，出现在边墙中上部（表6）。有水压力时，洞柱岩体最大主应力分布云图基本保持不变，最大压应力降低0.2 MPa左右。承受水压力一侧的洞室围岩，拉应力最大值（0.189 MPa）以及一般量值拉应力的范围均有所降低。调压室岔管部位围岩最大压应力大约降低0.2 MPa，最大拉应力降低0.01 MPa（图18）。因此，总体来看，调压室水压力引起的围岩应力状态变化是极小的。

开挖完毕后，尾调室锚杆最大应力为203 MPa；调压室水压力作用前后，各特征点处锚杆应力变化极小。与开挖完毕时相比，水压力作用下洞间岩柱的破坏区范围基本没有变化（图19），顶端耦合区域1内微裂纹单元数增加11个，岩柱中部耦合区域2内微裂纹数量增加47个，说明调压室水压力引起的围岩塑性区分布范围及深度变化极小。

由围岩宏观受力特性可以看出，尾水调压室洞间岩柱底板附近是岩柱最大主应力集中的部位，在此处设置耦合区域3以观察底板围岩在检修工况下岩柱承担单方向水压力时的细观变形与破坏特性。耦合区域3上半部分位于洞间岩柱内，下半部分位于岩柱底板以下围岩内，左侧临近岔管开挖临空面。在水压力作用下洞间岩柱有以底部转角为中心发生侧向位移的趋势，上半部分的侧向位移明显大于下半部分，位移最大值出现在施加荷载一侧的左顶角，至右下角越来越小。说明洞间岩柱的最大侧向位移不在耦合区域中间（即底板附近），结合连续单元的位移云图（图20）可以看出，岩柱1/3高度处侧向位移最大。

开挖过程以及有无水压力工况下的耦合区域3微裂纹分布形态见图21。可以看出，底板围岩内的细观损伤主要出现在开挖期间，即第5期岔管开挖时，且靠近开挖面附近的微裂纹密度较大，远离开挖面时微裂纹密度较小。水压力作用下与开挖完毕时相比，微裂纹数量仅增加4个，说明水压力几乎没有加深底板附近围岩的破坏程度。

5  结 论

本文提出了一种软硬混合平行黏结模型的细观参数快速标定法，其根据给定的岩石（体）力学参数，快速将宏观-细观参数对应起来，然后构建了基于颗粒离散元与有限差分耦合的旭龙地下电站尾水调压室PFC 3D-FLAC 3D三维离散-连续耦合分析模型，用于开挖期和检修期侧向水压力下尾调室洞间岩柱围岩稳定宏-细观特性分析，主要结论如下：（1） 尾调室洞间岩柱顶端最大位移为14.6 mm，岩柱两侧的变形随高度降低而呈线性减小趋势，两侧位移矢量相对岩柱中心轴基本呈对称分布。洞间岩柱上半段22.7 m的高度存在塑形贯通区，下半段31.5 m高度范围内塑性区深度呈线性降低，中间仍保留有一定范围的弹性区，到岩柱底板处围岩塑性区几乎为0。

（2） 尾水调压室检修工况下洞间岩柱承担单方向水压力时，最大位移0.75 mm位于施加荷载一侧的边墙中下部，从山体外到山体内随着远离荷载作用面，水压引起的岩柱位移增量逐步减小。承受水压力一侧的洞室围岩，最大压应力降低0.2 MPa左右，最大拉应力降低0.006 MPa，因此调压室水压力引起的围岩变形与应力增量变化是极小的。

（3） 研究结果表明，旭龙地下电站尾水调压室洞间岩柱存在明显的塑性贯通区，局部稳定性较差，有必要在工程建设期开展尾水调压室及尾水支洞岩墩塑性贯通区专项支护方案研究，确保旭龙地下电站工程的安全建设与运行。

参考文献：［1］  樊启祥，林鹏，蒋树，等.金沙江下游大型水电站岩石力学与工程综述［J］.清华大学学报（自然科学版），2020，60（7）：537-556.

［2］  樊启祥，王义锋，裴建良，等.大型水电工程建设岩石力学工程实践［J］.人民长江，2018，49（16）：76-86.

［3］  朱维申，李晓静，郭彦双，等.地下大型洞室群稳定性的系统性研究［J］.岩石力学与工程学报，2004，23（10）：1689-1693.

［4］  邵国建，卓家寿，章青.岩体稳定性分析与评判准则研究［J］.岩石力学与工程学报，2003，22（5）：691-696.

［5］  李术才，李树忱，朱维申，等.三峡右岸地下电站厂房围岩稳定性断裂损伤分析［J］.岩土力学，2000，21（3）：193-197.

［6］  李宁，陈蕴生，陈方方，等.地下洞室围岩稳定性评判方法新探讨［J］.岩石力学与工程学报，2006，25（9）：1941-1944.

［7］  晏莉，阳军生，张学民，等.水平互层岩体并行隧道中间岩柱稳定分析［J］.岩石力学与工程学报，2009，28（增1）：2898-2904.

［8］  郭佳奇，乔春生，曹茜.侧部高压富水溶腔与隧道间岩柱安全厚度的研究［J］.现代隧道技术，2010，47（6）：10-16.

［9］  武爱玲，宋宝生.南水北调中线吴庄隧洞洞间岩体厚度的分析［J］.水科学与工程技术，2009（6）：56-57.

［10］王登科，骆建军，高立平，等.基于爆破等效荷载的大型地下洞室群合理间距分析［J］.中南大学学报（自然科学版），2022，53（6）：2224-2233.

［11］段亚刚.地下大型储备库洞室断面形状优化及合理间距研究［D］.北京：北京交通大学，2007.

［12］崔思严.地下厂房洞室群岩柱厚度、洞跨与洞高的统计相关分析［J］.四川水力发电，2006，25（5）：81-84.

［13］李仲奎，戴荣，姜逸明.FLAC3D分析中的初始应力场生成及在大型地下洞室群计算中的应用［J］.岩石力学与工程学报，2002，21（增2）：2387-2392.

［14］曾静，盛谦，廖红建，等.佛子岭抽水蓄能水电站地下厂房施工开挖过程的FLAC3D数值模拟［J］.岩土力学，2006（4）：637-642.

［15］刘建华，朱维申，李术才，等.小浪底水利枢纽地下厂房岩体流变与稳定性FLAC3D数值分析［J］.岩石力学与工程学报，2005，24（14）：2484-2489.

［16］李冬冬，胡浩然，肖明，等.基于PFC-FLAC离散-连续耦合的隧洞开挖与锚杆支护颗粒流模型［J］.武汉大学学报（工学版），2024，57（3）：286-294.

［17］李冬冬，胡浩然，肖明，等.全长粘结锚杆支护隧洞围岩的颗粒离散元模拟与细观作用机理研究［J］.武汉大学学报（工学版），2024，57（1）：37-44.

［18］李冬冬，盛谦，肖明，等.基于改进颗粒流声发射片的地下厂房洞室围岩局部损伤细观机制研究［J］.岩土力学，2022，43（增2）：117-129.

（编辑：郭甜甜）

Macro and micro characteristics of surrounding rock of rock pillar between tail-race surge chamber caverns in Xulong Power Station

LI Dongdong，CHEN Jieping，WU Qiubo，SUN Haiqing

（Changjiang Survey，Planning，Design and Research Co.，Ltd.，Wuhan 430010，China）

Abstract：

To couple continuous and discontinuous analysis methods for the stability analysis of surrounding rock in underground power stations，a rapid calibration method for mesoscopic parameters based on a soft-hard mixed parallel bond model was implemented.This method can quickly correspond to the given rock macroscopic mechanical parameters to PFC model mesoscopic contact parameters.A three-dimensional discrete continuous coupling analysis model for the tail-race surge chamber of Xulong Power Station based on the coupling of particle discrete element PFC 3D and finite difference FLAC 3D was constructed.The macro-micro deformation and failure characteristics of rock pillars between tail-race surge chamber caverns during excavation were studied，as well as the impact of lateral water pressure on the rock pillar stability.The results showed that the deformation and stress increment of surrounding rock caused by the water pressure in the surge chamber under maintenance condition were minimal，but there was a plastic penetration zone at the height of 22.7 m in the upper half of the rock pillar between the caverns，with poor local stability.Thus it is necessary to carry out a special support scheme study on the plastic penetration zone of the tail-race surge chamber and tail-race branch tunnel rock piers during the construction period to ensure the safe construction and operation of the Xulong Power Station project.

Key words：

tail-race surge chamber; rock pillar between caverns; FLAC 3D; discrete-continuous coupling model; plastic penetration zone