认识方程

郭秋妹

方程的意义

什么是方程呢？以前遇到的“100-（）=45”“20×（）= 120”之类的题目，其实就是方程的雏形。我们可以先观察下图。

天平左右平衡，说明了图一中50+20=70，图二中50+？=70。如果用x表示图二中的“？”，50+？=70便可转化为50+x=70。比较50+ 20=70和50+x=70，可以发现：两个算式都是等式，50+20=70中，三个量都知道；50+x=70中，一个加数不知道，即有一个量是未知的，像这样含有未知数的等式就是方程。从上面的方程和等式可以看出，等式不一定是方程，但方程一定是等式。方程一定要同时具备“未知数”和“等式”这两个条件。

方程的解法

“移项变号”是解方程的重要方法。这种方法是根据“等式两边都加上（或减去）同一个数，等式仍然成立”和“等式两边都乘或除以同一个数（0除外），等式成立”，把方程含有未知数那个式子中不是未知数的项连同运算符号移到方程另一边，并且加号变减号，减号变加号，乘号变除号，除号变乘号，计算后得到方程的解。

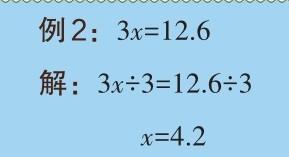
如例1，就是把方程含有未知数式子“x-4.5”中不是未知数的项“-4.5”，应用“等式两边都加上同一个数，等式仍然成立”，在方程两边都加上4.5，相当于把“-4.5”移到方程的另一边，从而得出方程的解。

如例2，就是把方程含有未知数式子“3x”中不是未知数的项“×3”，应用“等式两边都除以同一个数（0除外），等式成立”，在方程两边都除以3，相当于把“×3”移到方程的另一边，从而得出方程的解。

方程的演变

早在3600年前，古埃及人写在草纸上的数学问题中，就涉及了含有未知数的等式；250年前后，古希腊数学家丢番图写了一本数学巨著《算术》，引入了未知数的概念，并使用符号表示未知数；约820年，阿拉伯数学家阿尔·花剌子米曾写过一本名叫《代数学》的书，首次在解方程中引入对消和移项的方法。在我国，成书于1世纪前后的《九章算术》已有方程的思想；12世纪前后，我国数学家开始用专门的符号来表示未知数。